圆锥滚子轴承振动数据改进Huber M稳健化处理方法研究
党凤魁,徐永智,丁慧玲,刘 建
(1.河南科技大学 a.农业装备工程学院; b.高端轴承摩擦学技术与应用国家地方联合工程实验室,河南 洛阳 471023;2.三门峡职业技术学院,河南 三门峡 472000)
0 引言
数据稳健性对数据分析结果的可靠性有着重要的作用[1]。目前,研究数据稳健性方法均要求明确数据分布的密度函数、趋势项或者显著性水平[2-4],很少涉及未知分布数据的稳健性分析。然而,在实际实验中,受到环境、温度、湿度、载荷和润滑等多种因素影响及相互耦合,数据的分布类型、趋势项及显著性水平很难预知[5-8]。分布数据的稳健性是保证分析结果置信水平的关键因素,如何分析未知分布数据的稳健性成为统计学面临的重要难题。
中位数估计和Huber M估计是统计学中两种最优估计方法。中位数是极大极小化准则下最优位置估计,平均值受离散数据影响,为不稳健数据。根据大数定理和中心极限定理,中位数等于平均值,所以中位数可以作为平均值是否稳健的判断标准,两者越接近,数据越稳健。Huber M估计不需要知道数据分布类型,是以边界数据替换的方法提高数据稳健性[1]。因此,为了分析未知分布数据的稳健性,将中位数估计和Huber M估计的优点进行有机融入,得到一种改进的Huber M估计方法。
滚动轴承振动的稳定性能对高精密设备运行的可靠性、安全性有重要的作用,受到轴承工程界与理论界的关注[9-10]。一些学者采用统计学方法[11-12]、非统计学方法[13-14]对滚动轴承振动性能进行了研究,发现滚动轴承振动类型出现多样性,属于分布未知的时间序列。时间序列的未知分布特征是乏信息的重要内容之一,其稳健性是分析数据特征的前提,目前对数据进行稳健处理的方法主要有统计学[15]、非统计学[16]两种,其中统计学需要数据分布类型、显著性水平[17-18],非统计学则需要数据的显著性水平[19-20]。因此,仅统计学无法很好地解决未知分布时间序列的稳健性问题。改进的Huber M方法融合了中位数及Huber M方法的优点,对滚动轴承振动数据进行分析,确定滚动轴承振动数据的显著性水平及稳健性。
1 数学模型构建
根据时间变量t将实验数据离散,在设定时间间隔下,采集到t时刻滚动轴承振动的数据序列向量:
X={x(t)},
(1)
其中:x(t)为时刻t的振动数据,t=1,2,…,N。
从向量X中抽取第m套轴承的振动数据,构成时刻t的振动向量:
Xm={xm(t)},t=1,2,…,N;m=1,2,…,N。
(2)
根据从小到大的顺序,实验数据排列构成振动数据次序统计量Ym:
Ym={ym(t)},t=1,2,…,N;m=1,2,…,N。
(3)
找出次序统计量Ym序列的振动中位数βm:
(4)
根据改进的Huber M方法原理,获得滚动轴承振动稳健数据序列。
设次序统计量序列1,2,…,N中,yi(b)和yi(e)分别为第b个数据和第e个数据,yi(b)为最小值、βi为中位数、yi(e)为最大值。
定义1 将稳健数据按照从小到大的顺序重新进行排列,中位数左边的数据yi(b),…,βi为左序列数据,其中yi(b)为首数据,数据个数为n1。中位数右边的数据βi,…,yi(e)为右序列,其中yi(e)为右序列尾数据,数据个数为n2。
根据改进的Huber M估计方法[1]原理,当实验数据次序统计量出现异常时,若yi(n)≤yi(b),则用yi(b)代替yi(n);若yi(n)≥yi(e),则用yi(e)代替yi(n),处理后得到一组新的数据序列Zi(n1,n2):
Zi(n1,n2)={zi(n;n1,n2)};i=1,2,…,m;n=1,2,…,N,
(5)
其中:Zi(n1,n2)为稳健数据序列;zi(n;n1,n2)为稳健数据序列中的第n个数据。
根据近代统计学理论[1],获得改进Huber M估计方法稳健数据序列平均值ηi(n1,n2):
(6)
其中:ηi(n1,n2)为改进Huber M估计方法稳健数据序列平均值。
因为平均值与中位数值越接近,表明数据的稳健性越好。进一步以平均值与中位数的绝对差来评估改进Huber M估计方法稳健数据的稳健性。根据式(4)和式(6),获得改进Huber M估计方法实验数据稳健数据序列平均值估计与绝对值排序序列中位数估计的绝对差Di(n1,n2):
Di(n1,n2)=|βi-ηi(n1,n2)|,i=1,2,…,m。
(7)
根据近代统计学理论[1],实验数据个数N为偶数时,取n1=n2=1,2,…,N/2;N为奇数时,取n1=n2=1,2,…,(N+1)/2。
取不同的n1和n2值,得到不同的Huber M估计方法稳健数据序列平均值与中位数的绝对差Di(n1,n2),简化为Di。
根据近代统计学稳健性理论[1],显著性水平的范围为α=(n1+n2)/N=0~0.1。
找到绝对差序列中Di(n1,n2)的最小值Dimin,即Huber M估计方法稳健数据平均值最接近中位数的稳健数据列,Dimin所对应的左序列首数据,以及yi(b)和右序列尾数据yi(e),分别为记为Ki1和Ki2。Ki1和Ki2之间的数据为稳健数据,Ki1和Ki2之外的数据为不稳健数据,用相应的Ki1和Ki2,上述数据组成稳健数据Pi。
稳健数据Pi按照原数据顺序进行排列,就得到实验数据的稳健数据。
Pi={xRi(n)},n=1,2,…,N,i=1,2,…,m,
(8)
其中:Pi为实验数据稳健数据;xRi(n)为第i实验样本中第n个时间间隔的稳健实验数据。
Dimin所对应的显著性水平,即时间序列的显著性水平,Ki1和Ki2为实验数据的边界值。根据边界值Ki1和Ki2,得到稳健数据区间[Ki1,Ki2]。
数据稳健性指标为Qi、QRi:
Qi=Di;
(9)
QRi=DRi,
(10)
该数值越小,表明数据序列均值越接近中位数,数据序列越稳健。
数据离散性指标为极差Ri:
Ri=ximax-ximin;
(11)
RRi=xRimax-xRimin,
(12)
该数值越小,表明数据序列离散性越好。
2 数据处理与结果分析
为了验证上述方法,以30204圆锥滚子轴承为研究对象,测量其振动速度时间序列,分析振动速度的稳健性特征。该实验采用B1010测量装置,如图1所示,轴承内圈由主轴驱动,外圈端面施加轴向载荷,外圈周向间隔120°放置3个速度传感器,测试轴承径向速度信号。其中,主轴转速为1 800 r/min,轴向载荷为60 N,传感器综合输出误差小于1 μm,试验环境温度为20 ℃左右,相对湿度小于70%,无其他振动源,实验振动标准依据JB/T 10236—2001,检验方法依据JB/T 5313—2001。

图1 测量装置
30204圆锥滚子轴承共4套,每间隔1 min测量一个数据,每套轴承测量901个振动数据。图2为4套滚动轴承的振动数据,由图2可以看出:在相同测试条件下,1~4套轴承的振动幅度不同,数据变化趋势也不相同。其中,轴承3的振动数据值幅度最大,其振动趋势越来越平稳,呈现好的趋势状态;轴承1、2的振动数据范围次之,其振动趋势复杂多变,有恶化的趋势;轴承4的振动数据范围最小,振动趋势较平稳,有增大趋向。总体来说,4套轴承的振动数据呈现离散性较大、趋势未知、分布未知的特征。为了分析数据的稳健性,原始数据的特征参数见表1。

(a) 第1套轴承 (b) 第2套轴承

(c) 第3套轴承 (d) 第4套轴承
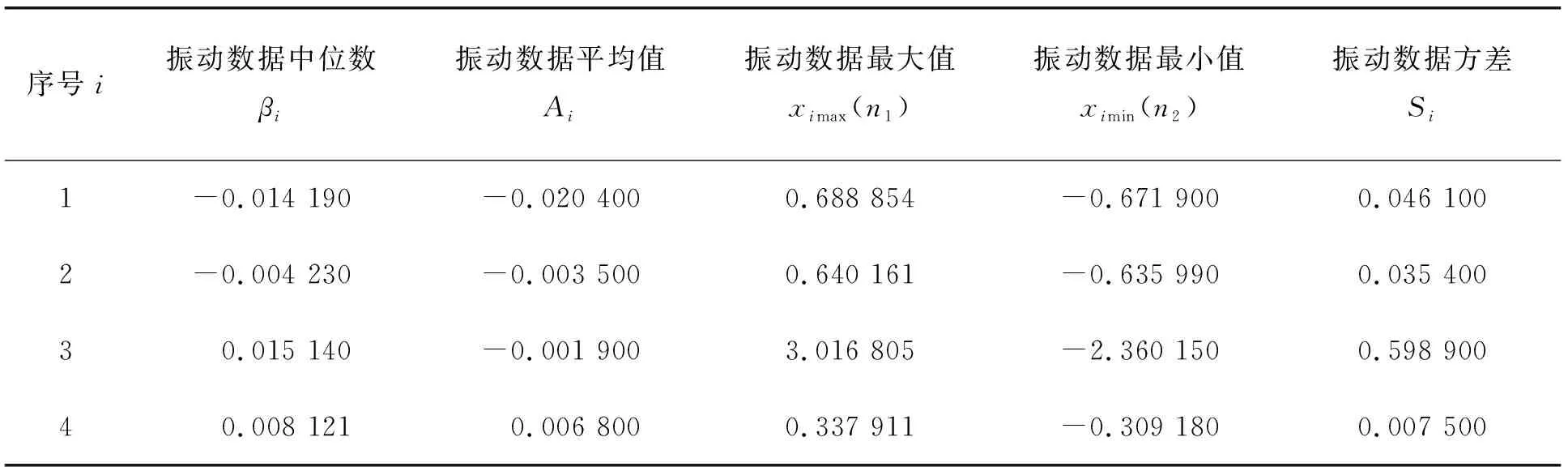
表1 30204圆锥滚子轴承振动性能参数 μm/s
图3为30204圆锥滚子轴承改进Huber M方法稳健数据列绝对差Di图。由图3可知:随着显著性水平α的提高,第1、2、4套轴承的绝对差Di值减小,而第3套轴承的Di值增加。表明随着α的提高,第1、2、4套轴承实验数据的稳健性提高,第3套轴承稳健性降低。根据中位数估计与Huber M估计融合方法,可知第1、2、4套轴承的显著性水平为0.1,第3套轴承的显著性水平为0,说明第1、2、4套轴承实验数据的稳健性置信水平为90%,第3套轴承的实验数据稳健性置信水平为100%。根据不同轴承的显著性水平得到不同轴承振动稳健数据的次序统计量Pi,见图4。

(a) 第1套轴承 (b) 第2套轴承

(c) 第3套轴承 (d) 第4套轴承
图4为滚动轴承振动稳健数据次序统计量的两种特征曲线,其中图4a为第1套轴承数据序列次序统计量曲线,呈先增加最后趋于平坦的趋势,第2、4套轴承数据序列与第1套轴承曲线走势一致。图4b为第3套轴承数据序列次序统计量曲线,呈先平稳增加最后突然剧增的趋势。4套轴承数据序列具有共同的特征:以中位数为中心、单调不减、有界连续,同时具有中位数估计、Huber M估计稳健性优点。为进一步分析滚动轴承振动数据的稳健性特点,将使用改进的Huber M方法稳健数据的特征参数列入表2。
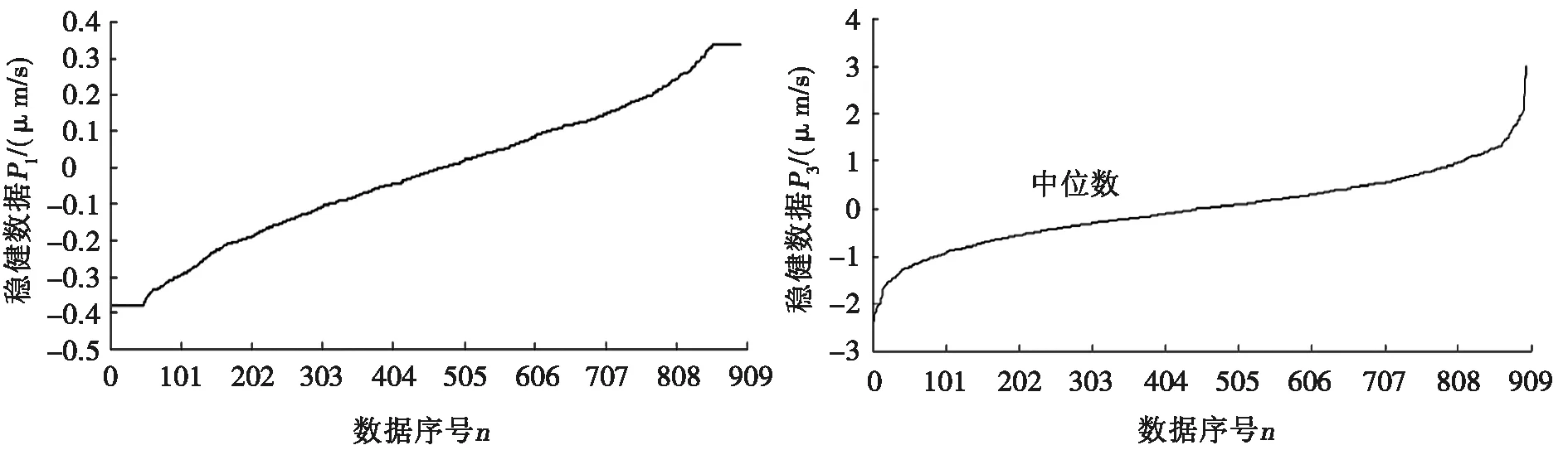
(a) 第1套轴承 (b) 第3套轴承

表2 滚动轴承振动稳健数据性能参数 μm/s
根据表1和表2,计算原数据和稳健数据的稳健指标和离散指标,见表3。

表3 原数据和稳健数据稳健指标离散指标对比 μm/s
由表1和表2可知:采用改进的Huber M估计融合方法处理后,稳健数据序列中位数不变、方差减小、最大值降低、最小值上升,中位数和平均值更接近。由表3可知:原数据的稳健指标均大于或等于稳健数据,说明经过中位数估计与Huber M估计融合方法稳健处理后,滚动轴承振动数据的稳健性提高。原数据的离散指标均大于或等于稳健数据。说明经过中位数估计与Huber M估计融合方法稳健处理后,滚动轴承振动稳健数据的离散性得到改善。
综合图3、表1和表2的结果,该方法可以确定数据的置信水平、稳健数据边界值,提高数据的稳健性。改进的Huber方法是在一定显著性水平范围内,采用Huber M方法处理数据,以平均值接近中位数的程度作为稳健判断依据,确定数据的置信水平、稳健数据边界值。
改进的Huber M为分布类型未知、置信水平不确定的复杂实验数据的稳健处理提供了一种可行方法。目前,关于中位数与平均值的接近程度的理论研究尚未完善,数据置信水平范围的确定方面参考文献较少,是作者及课题组成员进一步研究和探讨的方向。
3 结束语
本文提出改进的Huber M方法,以时间序列平均值最接近中位数为稳健数据判断标准,为未知分布实验数据的置信水平、Huber M边界值的确定提供了一种更为稳健的方法。中位数体现数据位置,Huber M体现数据整体性,两者融合可以体现数据的位置及整体性。改进Huber M方法处理后轴承振动数据的稳健指标和离散指标均减小,数据稳健性提高。

