用Python分析数学黑洞——冰雹猜想

王德贵

通过前几期文章，我们对于数学黑洞有了一定的了解，今天我们继续用Python来分析和研究数学黑洞——“冰雹猜想”。

我们先来了解一下“冰雹猜想”的来历。

1976年的一天，《华盛顿邮报》于头版头条报道了一条数学新闻。文中记叙了这样一个故事：

70年代中期，美国各所名牌大学校园内，人们都像发疯一般，夜以继日，废寝忘食地玩弄一种数学游戏。这个游戏十分简单：任意写出一个正整数N，并且按照以下的规律进行变换：

如果是个奇数，则下一步变成3N+1。

如果是个偶数，则下一步变成N/2。

不单单是学生，甚至连教师、研究员、教授与学究都纷纷加入。为什么这种游戏的魅力经久不衰？因为人们发现，无论N是怎样一个数字，最终都无法逃脱回到谷底1。准确地说，是无法逃出落入底部的4-2-1循环，永远也逃不出这样的宿命。

这就是著名的“冰雹猜想”，也叫“角谷猜想”“考拉兹猜想”“3X+1猜想”或“归一问题”，也是著名的数学黑洞之一。

通过输入一个正整数，判断其奇偶性，如果是偶数则除以2，如果是奇数则乘以3加1，如此反复，直到结果为1。

所有循环条件就是结果不为“1”，因此使用while循环比较好，下面看程序设计。

程序涉及中国电子学会Python编程等级考试二级考试的内容：程序的三种结构，即顺序结构、分支结构和循环结构。

经过几次数学黑洞这类问题的研究，类似的程序设计对我们来说已经比较简单了，语句也很好理解（图1）。

if分支语句中的print（）语句是为了能看到在做怎样的运算，最后输出结果（图2）。

用27测试，27的运算过程如图3，没想到27居然需要这么多步才能进入黑洞。

上述程序为递推法，我们也可以用递归法。那么就会涉及到等级考试四级的递归知识点。程序如图4：

其验证结果与其他方法相同。

冰雹的最大魅力在于不可预知性。27是一个很小的自然数，但是如果按照上述方法进行运算，则它经过的运算过程上浮下沉异常剧烈：首先，27要经过77步的变换到达顶峰值9232，然后又经过34步到达谷底值1。全部的变换过程（称作“雹程”）需要111步，其顶峰值9232，接近原有数字27的342倍，如果以瀑布般的直线下落（2的N次方）来比较，则具有同样雹程的数字N要达到2的111次方。其对比何其惊人（图5）！

无论这个过程中的数值如何庞大，都会像瀑布一样迅速坠落。而其他的数字即使不是如此，在经过若干次的变换之后也必然会到纯偶数：4-2-1的循环。

冰雹猜想是否正确？一个思路是寻找反例，找到反例即说明猜想不成立。我们已经编写了计算机程序来验证一个数是否满足猜想。而且当X为正奇数时，3X+1一定为偶数，我们可对变换规则做出简化：若X为奇数，则变为（3X+1）/2;若X为偶数，则变为X/2。

采用这个简化规则可以加快程序运行速度。

據日本和美国的数学家攻关研究，小于7*10^11的所有的正整数，都符合这个规律。在这个庞大数量的验证中，并没有找到反例。这样看，冰雹猜想“很有可能”是正确的，但又不能绝对肯定。

不过，我们仍可通过编程来探究冰雹猜想的性质。以X=500为例，我们把每一次变换得到的数画成图（注意这里用了简化的变换规则）（图6）。

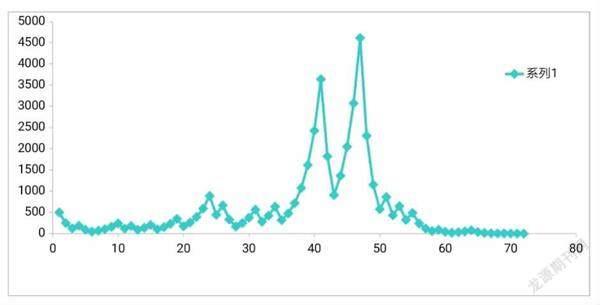
变换过程中数字大小存在快速的上升下降，到最高点后很快落至1。另外，我们可以探究X变为1所需变换次数N与X的关系。在2≤X≤1000范围内，N与X的关系图如图7（横轴为lg X，纵轴为N）。

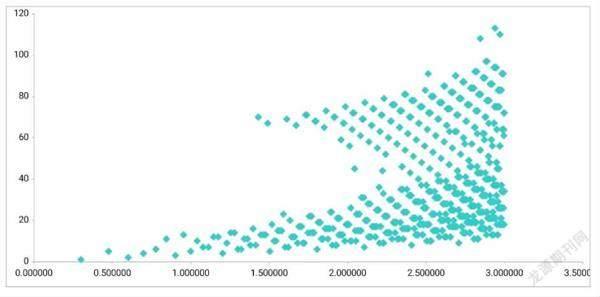
数据点大致分布在两条平行直线之间，由于横轴取了对数，这表明N随X大致以对数规律变化。当然，我们并不能确定这一结论在更大范围成立，这一结论是推测性的。

我看到过这项证明的英文版，有兴趣的朋友可以自己查一下。本文也是我自己的心得，有不妥之处，请各位老师和同学斧正！