基于中考备考的数学思想方法归纳和总结
陈杰


【摘要】如何在数学教学中培养学生的数学思考和数学思维能力,是应试教育向素质教育的一个重要转变。本文围绕中考备考,结合典型例题,侧重以数形结合思想、分类思想、转化思想等三种数学思想方法解决问题为例,阐述对数学思想方法进行归纳总结的重要性。
【关键词】中考备考;数学思想方法;归纳总结
有一种现象,不少的教师可能都深有感触——学生听教师讲解时是一听就懂,但自己独立解决问题时却是一做就错。很多学生以为是练习不够的缘故,于是不断反复循环练习,付出大量的时间和精力进行题海战,但收效甚微。《数学课程标准》在对初中阶段的教学建议中要求,“对于重要的数学思想方法应体现螺旋上升的、不断深化的过程,不宜集中体现”。这就要求教师在实际的教学过程中不断发现、总结、归纳、渗透数学思想方法。新课程理念告诉我们:“数学教学不仅是简单的知识传授,更重要的是学生数学思维能力的培养,使学生数学式地思考。”数学思想方法如转化思想、数形结合思想、分类思想、函数思想、方程思想等是数学学科的灵魂和精髓,是把知识转化为能力的桥梁,是解题规律的归纳总结,是达到触类旁通、摆脱题海的有效之路,是促进问题解决的“利器”。因此,在教学活动中,教师需要注重培养学生的数学思维能力,加强对数学思维方法的归纳和总结,切实提升学生的思维能力。如此才能使学生真正脱离“题海战”的恶性循环,提高学习效率。下面,笔者结合中考备考,对中考数学中重点考察的数学思想方法进行归纳和总结,目的在于抛砖引玉,为师生的数学中考备考带来一些启发和思考,使中考备考更有针对性。
一、数形结合思想
1.中考热点分析
数形结合思想是根据数学问题中的条件和结论之间的内在联系,既分析其数量关系,又揭示其几何意义,使数量关系和几何图形巧妙结合起来,并充分利用这种结合,探求解决问题的思路,使问题得以解决的思想方法,其实质是数与形之间的相互转化。
例1(2021年·广州):在平面直角坐标系xOy中,矩形OABC的点A在函数(x>0)的图象上,点C在函数(x<0)的图像上,若点B的横坐标为,则点A的坐标为( )。
2.思路分析
从代数的角度分析,点A在图像上,可设A,欲求点A坐标,需要结合题目的其它条件,设法用含m的代数式表示点C的坐标。本题的难点在于用含m的式子表示点C的坐标,这就需要探究点A、C间的相互联系。
从几何的角度分析,利用反比例系数K的几何意义,S△COE=×|-4|=2,S△AOD=
×1=,又可证△COE∽△OAD,故∴,,由A得C;至此,尚不能求解出m。这时,需要设法结合其它条件进一步找出A、C两点坐标的联系,建立等量关系,求解m;结合矩形OABC,AB=CO,故EO=xA-xB,即,解得或-4;因m>0,故,即A。
解題过程如下:
解:如图,作AD⊥x轴于D,CE⊥x轴于E,
∵四边形OABC是矩形,
∴∠AOC=90°,
∴∠AOD+∠COE=90°,
∵∠AOD+∠OAD=90°,
∴∠COE=∠OAD,
∵∠CEO=∠ODA,
∴△COE∽△OAD,
∴.
∵S△COE=×|-4|=2,S△AOD=×1=,
∴,
∴OE=2AD,CE=2OD,
设A(m>0),
∴C,
∴OE=0-(﹣)=,
∵点B的横坐标为﹣,
∴m-(﹣)=,
整理得2m2+7m-4=0,
∴m1=,m2=-4(舍去),
经检验,m=是方程的解,
∴A(,2),
故选A.
3.归纳总结
本题重点考查数形结合思想,既要分析图形的几何特征:反比例函数系数k的几何意义和矩形的性质,又要从代数角度分析反比例函数图象上点的坐标特征及点与点的坐标关系,通过建立等量关系,解方程求出点A坐标,其中表示出点的坐标是解题的关键。代数和几何有机结合,相互配合,综合性较强,对学生的综合能力有较高要求。
二、分类思想
1.中考热点分析
分类思想指的是如果一个命题的题设或结论具有不确定性,有多种可能情况,难以统一解答,就需要根据可能出现的情况分类加以讨论,最后综合归纳出问题的答案。分类讨论思想是中考的热点,试题综合性较强,能全面考察学生的思维能力、逻辑分析能力和探索问题能力。
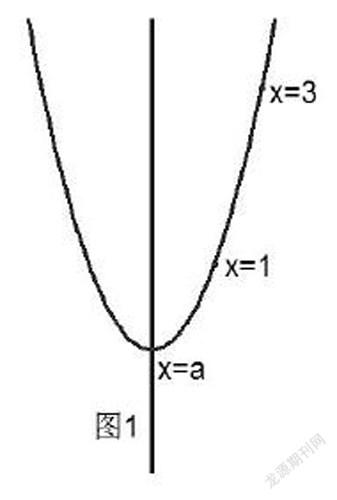
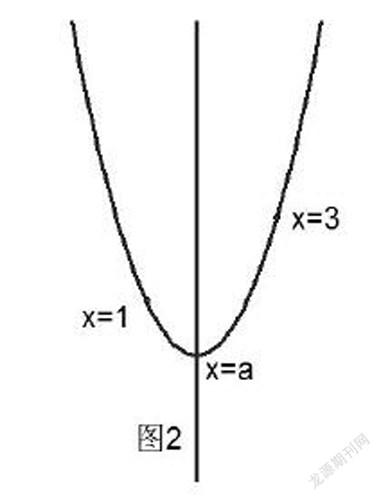
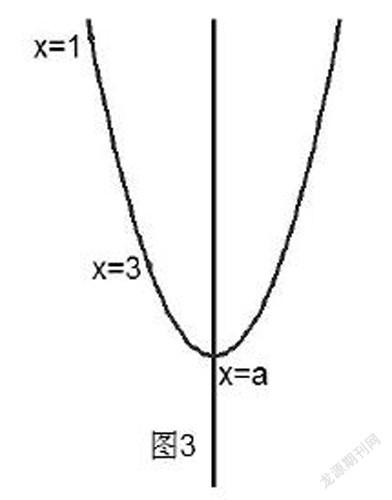
例2:已知关于x的二次函数y=(x-a)2+3-a2,当1≤x≤3时,函数有最小值2a,则a的值为_________。
2.思路分析
函数对称轴为直线x=a,若x取值范围是全体实数,此时当x=a时,ymin=3-a2;当x
解:分类讨论
(1)当对称轴x=a≤1时(如图1),y随x增大而增大,此时当x=1时ymin=(1-a)2+3-a2=2a,解得a=1满足a≤1,符合题意;
(2)当对称轴1≤x=a≤3时(如图2),此时当x=a时ymin=3-a2=2a,解得a=1或-3,其中a=1满足1≤a≤3,故此时a=1;
(3)当对称轴x=a≥3时(如图3),y随x的增大而减小,此时当x=3时,ymin=(3-a)2+3-a2=2a,解得a=,与a≥3矛盾,舍去;综上所述,a=1。
3.归纳总结
本题重点考察函数的增减性;二次函数对称轴两侧的增减性不同,由于对称轴x=a位置的不确定性,对于1≤x≤3,y取最小值的x也有不确定性,有三种可能:x=1,或x=3,或x=a,所以需要分类讨论。
三、转化思想
1.中考热点分析
转化思想是指在解决问题的过程中,对问题进行转化,化“未知”为“已知”,化“陌生”为“熟悉”,化“复杂”为“简单”,其核心是将有待解决的问题转化为已解决的问题,以便利用已有的结论解决问题。如,解方程时将“二元”转化为“一元”、“高次”转化为“低次”、“分式方程”转化为“整式方程”;将“多边形”问题转化为“三角形”等均是转化思想的集中体现。
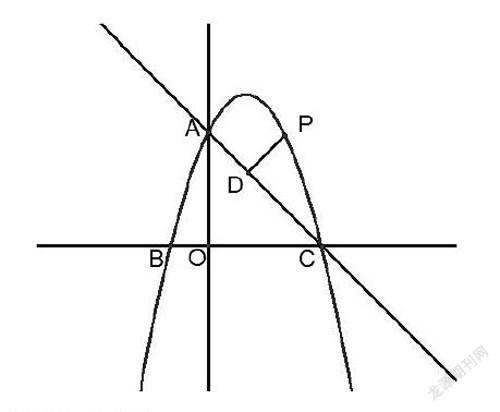
例3:如图,已知抛物线y=-x2+2x+3与y轴交于点A,与x轴交于B、C两点,连接AC。
(1)求直线AC的解析式;
(2)点P为直线AC上方抛物线上的一点,过点P作PD⊥AC于点D,当线段PD最长时,求点P的坐标。
2.思路分析
(1)分别令x=0,y=0,求得A(0,3)、B(-1,0)、C(3,0);由待定系数法可得直线AC解析式y=-x+3;
(2)P在抛物线上,可设点P(P,-P2+2P+3);欲求线段PD最值,须设法用含p的代数式表示PD,此时突破难度较大。可考虑转化思想,化难为易,把求PD最值问题转化为其它易求问题。
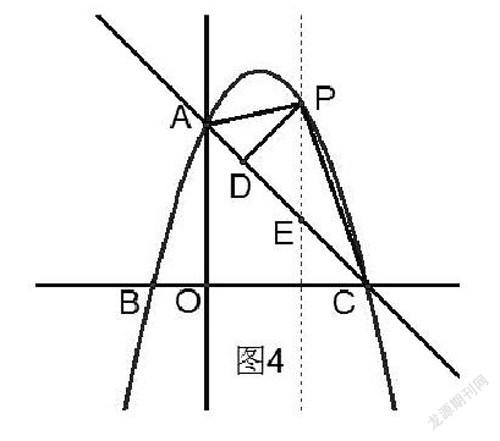
思路1:转化为面积问题(如图4)
把PD看成△ACP的高,由于线段AC为定值,,PD最大S△ACP面积最大。因此,求PD最大值可转化为求S△ACP最大值。利用割补法把△ACP割成△ACE、△PCE两个易求三角形的面积,求出S△ACP的表达式,再求最值。
思路2:转化为交点问题(如图5)
过点P作直线PE∥AC,由于平行线间距离处处相等,因此PD最大直线PE与抛物线仅有一个交点P;把求点P坐标转化为求直线PE与抛物线的交点问题处理。
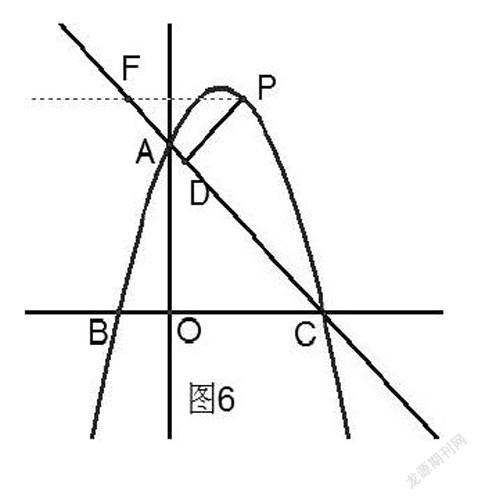
思路3:转化为其它线段的最值(如图6)
设点P(P,-P2+2P+3),直接用含P的代数式表示PD困难较大,设法转化成与PD有联系的易求线段(平行x轴或y轴的线段)处理。
过点P作直线PF∥x轴交直线AC于点F,易证△AOC∽△PDF,故,其中OA=3,AC=为定值,关键是表示出PF。由于PF∥x轴,P(P,-P2+2P+3),可设F(x,-P2+2P+3),又点F在直线AC:y=-x+3上,故F(P2-2P,-P2+2P+3),PF=xP-xF=P-(P2-2P)=-P2+3P,,最后求含p的二次函数最值。
解题过程如下:
解:点P在抛物线y=-x2+2x+3上,可设点P(P,-P2+2P+3).
解法1:转化为面积问题(如图4)
过点P作直线PE∥y轴交直线AC于点E,则E(P-P+3),故PE=yP-yE=-P2+2P+3-(-P+3)=-P2+3P,因此S△ACP=S△APE+S△CPE=PE(xC-xA)=(-p2+3P)=-P2+P,故当p=时,S△ACP最大值=,此时.
解法2:转化为交点问题(如图5)
解:过点P作直线PE∥AC,因为平行线间距离处处相等,故当直线PE与抛物线只有一个交点P时,PD有最大值;因为PE∥AC,且yAC=-x+3,故可设直线PE的解析式為yPE=-x+m,联立方程组,故-x+m=-x2+2x+3,整理得x2-3x+m-3=0,因为直线与抛物线只有一个交点,故△=(-3)2-4(m-3)=0,解得m=,此时x1=x2=,故.
解法3:转化为其它线段求最值(如图6)
解:过点P(P,-P2+2P+3),作直线PF∥x轴交直线AC于点F,因为∠PFD=∠ACO,∠PDF=∠AOC,故△AOC∽
△PDF,故;易得OA=3,AC=,由于PF∥x轴,P(P,
-P2+2P+3),可设F(x,-P2+2p+3),又点F在直线AC:y=-x+3上,故F(P2-2P,-P2+
2P+3),PF=xP-xF=P-(P2-2P)=-P2+3P,,故当p=时,PD有最大值,此时.
3.归纳总结
本题重点考察学生利用转化思想灵活解决问题的应变能力,全面考察了学生的逻辑分析能力,既要会利用点与点的坐标转化为线段长,也要会化难为易:把不规则图形的面积转化为规则图形的面积或把难求线段转化为易求线段或把求线段问题转化为求两个图像交点,方法手段灵活多样。
中考试题十分注重对数学思想方法的考察,特别是突出考察数学能力的综合性问题,其解决策略都蕴含着重要的数学思想方法,往往需要多种方法深度融合,你中有我、我中有你,对学生的综合能力有很高的要求。因此,在解题过程中,我们需要善于对题目背后的数学思想方法进行消化、归纳和总结,做到举一反三、触类旁通,不断提升解决问题的能力。
参考文献:
[1]王林全.现代数学教育研究概论[M].广东高等教育出版社,2005.
[2]数学课程标准研制组.全日制义务教育数学课程标准解读[M].北京师范大学出版社,2003.
[3]韩晓荣.几种重要的数学思想方法[OL].https://wenku.so.com/d/86b9cff0aa19c3f7360644963cf36bd5.
责任编辑 杨 杰

