高中数学直观想象素养培育途径例析

张金钟

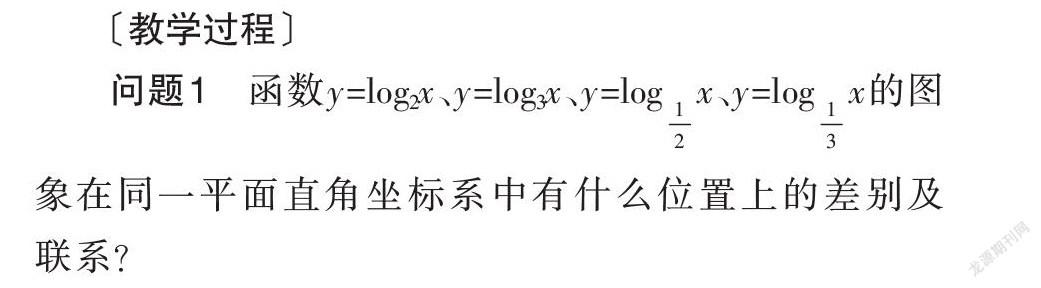
直观想象是对《普通高中数学课程标准》（2011年版）中提出的“几何直观”与“空间观念”的新发展.《普通高中数学课程标准》（2017版）指出：直观想象是指借助几何直观和空间想象感知事物的形态与变化，利用空间形式特别是图形，理解和解决数学问题的素养.

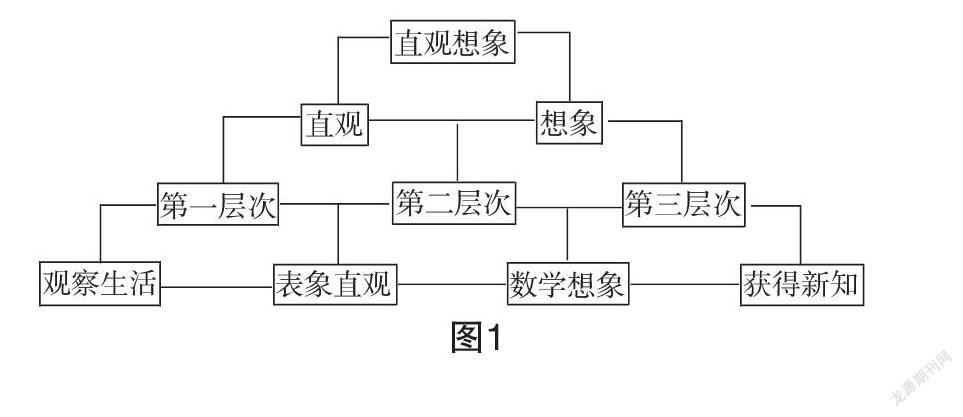
教师对学生直观想象核心素养的培养，需要遵循学生的认知规律，以及素养形成的必要阶段和层次，循序渐进.如图1，直观想象的形成基本分为两个阶段、三个层次、四个环节.第一阶段为直观，即学生在接触现实世界时通过直观观察而获得的感性认识，并初建模型，顺应数学来源于生活的思想;第二阶段为想象，在直观观察与建模的基础上，学生结合经验和已有数学知识进行猜想、探索、归纳、整合，获得新的知识体系和能力提升，符合数学服务于生活的本质.第一个层次重在提升数形结合的能力，发展几何直观和空间想象能力;第二个层次主要增强运用几何直观和空间想象思考问题的意识;第三个层次在于形成数学直观，在具体的情境中感悟事物的本质.四个环节主要包括观察生活、表象直观、数学想象和获得新知.

对于直观想象等核心素养的培养，教师不能单纯解读这个名词，而应通过发现、分析和解决问题的过程，引导学生领悟并掌握.在这里，笔者以“对数函数图象的形成”课程设计为例，探索学生直观想象能力的培养途径及其他核心素养的渗透在课堂教学中的体现.

一、基于列表描点法的图象形成探索

〔设计思路〕

列表描点法是探索函数图象的重要手段，也是几何直观直接的体现形式.通过列表描点法，教师能够让学生对对数函数的图象形成初步的认识，并在探索的过程中建立形与数的联系，构建数学问题的直观模型，为后续的性质研究及问题解决提供参考.

〔教学过程〕

问题1 结合指数函数图象的探索方式，思考：对数函数y=logx和y=log2x的图象是否可以同样探索？

师生活动：学生回顾指数函数，以及一元一次函数、一元二次函数、反比例函数等的图象探索方式，得出可以通过列表描点法探索对数函数的图象.

问题2 结合对数和指数的关联，思考：x的选择应控制在什么范围？

师生活动：x的选择应大于0.教师指导学生以小组合作的方式，通过不同列表，感知表象直观对图象内在实质提炼的重要作用.

问题3 回顾探索过程，思考：能否想象出y=logax（a>0且a≠1）的图象？

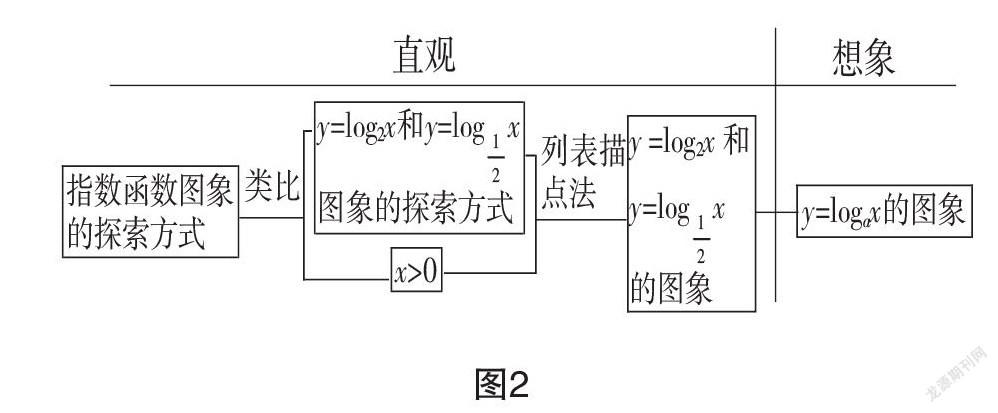
师生活动：通过几何直观的观察分析及与指数函数的类比探索，教师可以引导学生想象对数函数的图象，归纳出图象位于一、四象限，单调性受a不同取值范围的影响而改变等简单性质，如图2.

〔探索小结〕

利用基于列表描点法的图象形成探索，教师可引导学生从观察生活这一环节发现x>0的内在，据此列表、描点、连线，得到图象，并结合表象直观、逻辑推理、数学想象等抽象出y=logax（a>0且a≠1）的几何图形，提升他们的数形结合能力，发展几何直观和空间想象的能力及思考问题的意识，培育直观想象素养.

二、基于反函数法的图象形成探索

〔设计思路〕

反函数的概念在新课程教材中日益淡化，但借助反函数思想，将建立在特值上的指数、对数转换，抽象至实数范围内函数图象之间的关联，是培育直观想象中研究事物的位置关系、形态变化和变化规律的一种有效途径.

〔教学过程〕

问题1 结合对函数、反函数概念的认识，思考：什么样的函数才有反函数？

师生活动：学生讨论探索，得出“一一对应函数才有反函数”的结论，并得出对数函数和指数函数互为反函数.

问题2 结合对称性在图象上的体现，思考：互为反函数的两个函数的图象之间存在什么关联？

师生活动：结合对反函数概念的理解，教师引导学生得出指数函数中（a，b）与对数函数中（b，a）的對应关系，进而探索并证明出图象关于直线y=x对称的结论.

问题3 结合指数函数及互为反函数的两个函数图象之间的关联，思考：对数函数的图象是什么样子？

师生活动：结合尺规作图找对称点、折纸等直观想象及建模方式，得出对数函数的图象.

〔探索小结〕

直观想象的第二层次中增强几何直观与空间想象思考问题的意识在这里得到了很好的体现，通过借助反函数的概念及思想，从对指数函数的表象直观中萌发新的意识，学生提升了数学抽象能力.

三、基于数形互构的图象形成探索

〔设计思路〕

图象是性质的几何直观，性质又是图象的代数体现.通过函数的研究途径，我们可依次研究对数函数的定义域、值域、定点、单调性、奇偶性等性质，并通过各自的图象体现，探索对数函数的图象.

〔教学过程〕

问题1 结合指数、对数的转换关系，思考：对数函数的定义域和值域分别是什么？

师生活动：轻而易举地得出对数函数定义域为{x|x>0}，以及值域为R的结论.

问题2 结合定义域和值域的几何体现，思考：对数函数的图象呈现在什么区域？

师生活动：一、四象限，且与y轴无限接近但不相交.

问题3 结合幂函数、指数函数过定点的判断依据，类比对数运算公式，思考：对数函数是否也过某定点？

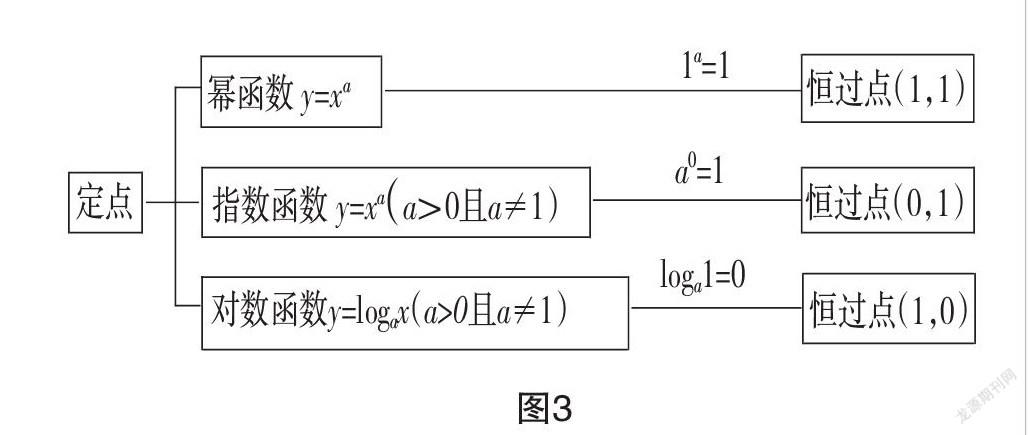
师生活动：类比幂运算1a=1、指数运算a0=1（a>0且a≠1），找到对数运算中loga1=0（a>0且a≠1），并得出对数函数过定点（1，0）的结论，并体现在图象中，如图3.

问题4 结合代数法判断单调性，思考：对数函数的单调性在图象中如何呈现？

师生活动：以小组合作的方式，回顾对数运算规则，分a>1和0<a<1两类证明并探索对数函数的单调性，得出“a>1时单调递增”和“0<a<1时单调递减”的结论.

问题5 结合代数法判断奇偶性，思考：对数函数是否具有奇偶性？在图象中如何呈现？

师生活动：函数具有奇偶性需先满足定义域对称，但对数函数不满足，故对数函数不具有奇偶性，图象不具有关于y轴或（0，0）的对称性.

问题6 结合以上探索，思考：对数函数的图象如何呈现？

师生活动：定义域与值域呈现在图象所在的区域上，定点呈现出底数不同的对数函数图象的共性，单调性呈现在图象的变化形式上，奇偶性呈现在图象的对称性上，如图4.

〔探索小结〕

数形结合是对直观想象最直接的认识，也是直观想象最常见的体现形式.数形互构的图象探索方式更深地体现出在具体情境中感悟事物本质，形成数学直观的重要性，促使学生在数学抽象中感悟并获得新知，促成直观想象核心素养的目标性培育.

四、基于教学软件的图象形成探索

〔设计思路〕

列表描点法能从未知世界中探索出图象的大体轮廓，反函数法需要有原始函数的支撑，数形互构法也仅能从某种程度上弥补前两种方法在图象探索上的不足，但不能动态、准确地体现底数变化对对数函数图象变化的精确影响.几何画板、GeoGebra、matlab等软件，就能很好地填补这个空白，让函数图象更精准，几何直观更准确，数学抽象更省力.

〔教学过程〕

问题1 函数y=log2x、y=log3x、y=logx、y=logx的图象在同一平面直角坐标系中有什么位置上的差别及联系？

师生活动：结合对数运算规则，能轻松得出底数互为倒数的两个函数的图象关于x轴对称，也能探索出底数的改变对图象增减幅度的影响，但稍显困难.

问题2 如何借助现代信息技术手段得到函数的准确图象，并观察动态变化？

师生活动：教师可借助几何画板、GeoGebra等软件，建立动态函数模型，通过参数改变体现图象变化，同时教会学生操作步骤，并在操作过程中培养学生的数据分析核心素养.

〔探索小结〕

科学是严肃的.直观想象是联系现实生活和科学理论的桥梁与纽带，是研究事物的形态与变化规律、分析和解决问题的重要手段.当然，我们同时也需要科学的技术与手段，进一步弥补想象中的不足，以及对比想象与实际之间的差距，以检验直观想象素养的培育效果.

综上所述，在对数函数图象的形成探究中，列表描点法依托生活中对数函数原型，用最朴实的方式对其进行观察，初立模型，引起表象直观;反函数法则在列表描点法的基础上誘发数学抽象，增强几何直观与空间想象思考问题的意识;数形互构法更是利用数形结合这一熟知手段，剖析性质与图象的内在联系，形成数学直观.

直观想象无处不在地体现在我们对生活的观察、认识和感悟中，在数学体系的构建和应用中处于十分重要的地位，更是数学学习过程中逐步形成的必备品质和关键能力.高中数学直观想象素养的培育，应以人为本，与时俱进，注重素养共进及学科融合.这些都需要我们一线教师在平时的教学中不断尝试、潜心研究.

◇责任编辑 邱 艳◇