2022年全国新高考Ⅰ卷数学第18题解析
⦿江苏省如东县掘港高级中学 张必荣
解三角形问题经常与平面几何、函数与方程、三角函数、平面向量、基本不等式等相关知识交汇与融合,充分落实新课标中“在知识交汇点处命题”的指导思想,是高考数学命题中的一个基本考点,倍受各方关注.
1 真题呈现



2 真题剖析
本题通过两小题的合理设置,以题设中的三角函数关系式为背景,通过三角恒等变换公式的应用与转化来求解对应的角的大小;并通过角之间的关系构建,以及正弦定理或平面几何知识的应用,化边为角,利用基本不等式来确定对应代数式的最值等.
借助问题的设置,很好地考查逻辑推理、数形结合、数学运算等数学核心素养.破解问题的关键在于善于审题,妙用定理(三角形的内角和定理、正弦定理等),借助公式(诱导公式、三角恒等变换公式等),采用有效的策略,合理化归与转化,优化解题过程,提升解题效益.
3 真题破解
解法1:倍角公式法.


点评:根据题设条件中的三角函数关系式,利用二倍角公式加以展开,通过两角和的余弦公式进行变形与转化,结合条件中角的信息求解即可;利用角之间的关系,综合正弦定理化边为角,结合诱导公式与二倍角公式的转化,利用基本不等式来确定相应的最值.二倍角公式是问题破解的关键,同时综合诱导公式、两角和与差公式等.
解法2:函数单调性法.
(1)由题意得

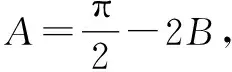

点评:根据题设条件中的三角函数关系式,利用诱导公式加以同构化处理,利用求导法确定对应三角函数的单调性,进而构建角之间的关系,并利用条件中角的信息来求解;利用角之间的关系,综合正弦定理化边为角,结合诱导公式与二倍角公式的转化,利用基本不等式来确定相应的最值.三角函数关系式的同构并结合函数单调性的判定,合理构建角之间的关系,是破解问题的关键.
解法3:半角公式法.


点评:根据题设条件中的三角函数关系式,利用半角公式、两角差的正切公式等加以变形,结合正切函数的单调性,构建角之间的关系,并利用条件中角的信息来求解;而求解三角形的边所对应的关系式的最值问题,同样可以利用基本不等式来确定相应的最值问题.半角公式的巧妙应用与转化,为角之间的关系构建提供更加广阔的思路.
解法4:平面几何法.






图1



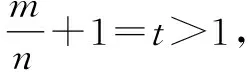

点评:根据题设条件中的三角函数关系式,利用三角形的内角和公式加以转化,通过两角差的正弦与余弦公式以及二倍角公式加以展开,进而化简三角关系式,求得对应的角;确定角B的大小以及对应角之间的关系后,要求解三角形的边所对应的关系式的最值,可以借助平面几何图形,引入参数,结合三角函数的定义、勾股定理等,结合几何直观转化,通过关系式的变形与参数的构建,借助基本不等式来确定最值.利用平面几何法分析与解决一些解三角形的相关问题,更加直观形象.
4 教学启示
4.1 思维视角归纳
破解解三角形问题的两种常见思维视角:
①代数角度.根据题设条件,利用正弦定理或余弦定理等,实现三角形中边与角之间的巧妙转化,进而构建关于三角形的角或者边等元素之间的关系进行分析与求解;利用平面直角坐标系的构建,通过相应的坐标表示来寻找三角形的角或者边等元素之间的关系来应用.代数角度中,经常还要综合三角函数、不等式、平面解析几何等相关知识来分析与处理.
②几何角度.根据题设条件,作出相应的平面几何图形,合理寻找平面几何图形中蕴藏的边或者角等元素之间的几何关系,通过直角三角形以及平面解析几何知识等来分析与求解.
4.2 思维能力培养
数学学习不能只注重“刷题”,做题要注重质量,少而精.通过做题掌握数学基础知识,提升数学思维能力,培养思维的多角度,避免思维定式,做到举一反三,是我们“促双减”过程中必须要思考的问题.

