“函数y=Asin(ωx+φ)的图象”教学设计

⦿云南师范大学 王 玉 孔德宏

1 教学分析

1.1 教学内容分析

“函数y=Asin(ωx+φ)”选自人教版2019年A版必修一第五章第六节.在上一课时，学生经历了筒车建模的过程，了解了每个参数的实际意义，为了研究更多做匀速圆周运动的物体的运动规律，可以通过研究函数图象进而研究其函数的性质，因此本节课重点是研究其函数的图象.根据从具体到抽象的原则，通过给参数赋值，从具体函数的讨论开始，把从函数y=sinx的图象到函数y=Asin(ωx+φ)的图象的变换过程分解为：先分别考察参数φ，ω，A对函数图象的影响，最后再对函数进行整合考察.教材也借助了具体函数的变化，让学生领会从简单到复杂、从特殊到一般的化归数学思想.

1.2 学情分析

在此之前，学生已经学习了正、余弦函数的图象及其相关性质，具备一定的基础，并且在之前的函数学习中学生已经基本掌握了一般函数图象的平移变换、对称变换等比较简单的函数图象变换方法，但对于伸缩变换还是初次明确提出并加以研究.本节课笔者将结合信息技术来进行教学，从认知心理上来讲，学生对通过GeoGebra动态展示函数图象是感兴趣的.

1.3 教学目标分析

(1)掌握参数φ，ω，A对函数图象的影响，理解参数φ，ω，A在匀速圆周运动中的实际意义.

(2)通过利用GeoGebra探索函数y=sinx到函数y=Asin(ωx+φ)的图象变换规律的过程，培养学生的观察能力、探索问题的能力以及直观想象的能力，在此过程中领会从特殊到一般、从具体到抽象的思维方法，从而达到从感性认识到理性认识的飞跃.

(3)本节课通过信息技术调动学生的积极性并渗透数形结合思想，让学生树立运动变化的观点，学会用运动变化的观点认识事物.

2 教学过程

2.1 结合软件，探索新知

问题1为了研究函数y=Asin(ωx+φ)的性质，需要研究函数的图象.函数y=Asin(ωx+φ)与我们所学的哪个函数相似？

问题2参数影响着函数图象的变化，如何对其进行研究？

问题3你会先研究哪个参数？

设计意图:通过观察思考,学生能够得出当A=1,ω=1,φ=0时即函数y=sinx，则函数y=Asin(ωx+φ)的图象可能会与函数y=sinx相似，让学生领会从特殊到一般的数学思想.学生能够提出需要通过限制变量的方法对其进行研究，先研究y=sin(x+φ)，y=sinωx，y=Asinx,再整合研究y=Asin(ωx+φ).学生学过了图象的平移变换，因此提出先研究参数φ.

探究1:探索φ对y=sin(x+φ)图象的影响.

图1

问题5你能从数学逻辑推理角度进行证明吗？需要证明什么呢？

学生通过小组合作得出数学证明后的结论：一般地，当动点的起点位置Q所对应的角为φ时，对应的函数是y=sin(x+φ)(φ≠0),把正弦曲线上的所有点向左(当φ>0时)或向右(当φ<0时)平移|φ|个单位长度，就得到函数y=sin(x+φ)的图象.

探究2:类比探究分别得出ω，A对函数图象的影响.

类比探究的方法：通过GeoGebra实验观察，从运动变化角度进行理解，再通过数学证明.

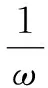
设计意图:类比探究是一种重要的数学思想和方法.在探究φ的过程中学生已经掌握基本的研究思路和方法，因此可以采用类比的方法对ω，A进行探究.学生是课堂的主体，将任务交给学生能够激发学生的兴趣并且有利于发展其自主思考、团结协作和表达交流的能力.

探究3:整合研究，深化理解.

问题6你能总结从正弦函数图象通过图象变换得到y=Asin(ωx+φ)(A>0,ω>0)图象的过程与方法吗？

设计意图:对函数进行整合研究，可以培养学生的总结能力和思维能力；同时，让学生理解只要将函数y=Asin(ωx+φ)的性质研究清楚，就能够把握这类事物的运动规律.

2.2 空出留白，深度学习

在研究函数y=Asin(ωx+φ)的图象时，为了方便进行研究选取的是A>0,ω>0，那么这两个参数只能取A>0,ω>0吗？如果取A<0,ω<0时图象会如何？

在最后进行整合时是通过变化φ，ω，A这样的顺序将正弦曲线变化为函数y=Asin(ωx+φ)，那如果不按照这样的变化顺序呢？例如通过变化ω，φ，A这样的顺序会是怎样的情况呢？

设计意图:这两个问题留给学生课后进行深度学习，有利于培养学生的逻辑思维能力；同时，让学生明白函数y=Asin(ωx+φ)的参数可以取任意实数，只是在现实世界中大多数事物都是在A>0,ω>0的取值范围内.

3 教学反思

本节课的研究思路：利用GeoGebra研究函数的图象，通过“形”观察、“运动变化”解释、“数学”证明对参数如何影响函数图象进行探究.在此过程中，利用软件GeoGebra进行实验让学生能够更加直观地进行观察，有利于培养学生的直观想象能力；利用类比探究ω，A对函数图象的影响，有助于培养学生的类比思想、团结协作能力和沟通表达交流的能力.