直线参数方程及其应用浅析

⦿重庆市涪陵高级中学校 张雨灵

1 引言

直线与二次曲线相交、相切、相离等位置关系的判断以及由此引出的系列问题是高中解析几何专题要讨论的问题，这些问题是训练学生逻辑推理、数学运算、直观想象等核心素养的重要载体.解析几何的基本思想是用代数的方法来研究解决几何问题，所以在求解解析几何相关问题的过程中往往需要大量计算，这是解析几何问题的主要难点所在.而突破这一难点，除了需要充分挖掘利用几何信息简化计算外，有时还需根据具体问题合理选择直线或曲线方程的形式.比如，利用直线方程参数形式，不仅可以在解决二次曲线和直线相交时的求点坐标、距离、弦长、弦的直线方程等系列问题中简化计算,而且还可以有效解决与弦的中点有关的轨迹方程，以及曲线的切线方程等问题.下面先探讨直线的参数方程中参数t的几何意义及其应用.

1.1 直线参数方程中参数t的几何意义

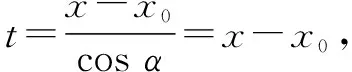
1.2 联立直线与二次曲线方程

设缺xy项的一般二次曲线Γ的方程为Ax2+Cy2+Dx+Ey+F=0(其中A,C不同时为0)，联立二次曲线Γ与直线l的参数方程,得

(*)

不妨记

m=Acos2α+Csin2α

①

n=2Ax0cosα+2Cy0sinα+Dcosα+Esinα

②

③

则(*)式可简记为

mt2+nt+w=0.

④

下文将运用直线l的参数方程并结合参数t的几何意义，解决直线l与二次曲线Γ的常见问题.

2 判断直线l与二次曲线C的位置关系

将直线l的参数方程与二次曲线Γ联立，整理的方程记为④，则其判别式为Δ=n2-4mw.当Δ>0时，直线l与二次曲线Γ相交；当Δ=0时，直线l与二次曲线Γ相切；当Δ<0时，直线与二次曲线Γ相离.

由Δ=8>0知，直线l与椭圆Γ相交.

3 直线与二次曲线的交点或弦长问题

将直线l参数方程与二次曲线Γ联立，整理得方程④，当Δ>0时，记两实根分别为

(1)由直线参数方程中参数t的意义知，t1,t2分别为直线l与二次曲线Γ交点A，B所对应的参数，由此可求出交点A，B坐标为

A(x0+t1cosα,y0+t1sinα)，

B(x0+t2cosα,y0+t2sinα).

图1

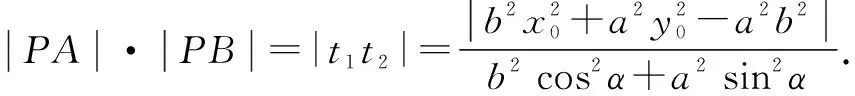
所以|PA|·|PB|=|PC|·|PD|，从而A，B，C，D四点共圆.

4 二次曲线Γ中与弦中点有关的问题

4.1 求二次曲线Γ平行弦中点所满足的轨迹方程

因为M(x′,y′)为中点，所以有t1+t2=0，即x′+3y′=0.所以中点M的轨迹方程为x+3y=0.

4.2 求二次曲线过定点P(x0,y0)的弦的中点的轨迹方程

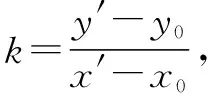
2A(x′)2+2C(y′)2-(2Ax0-D)x′-(2Cy0-E)y′-(Dx0+Ey0)=0

①

即中点M(x′,y′)坐标满足①式，即得中点M的轨迹方程.

当动弦的斜率不存在时，联立直线x=x0及二次曲线方程，求出交点坐标，再求出中点，通过验证中点是否满足斜率k存在时的方程①来决定是否需要补充这一点.

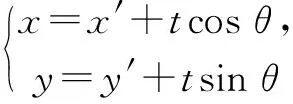
当直线l的斜率不存在时，直线与双曲线无交点.

综上所述，弦中点的轨迹方程为4x2-y2+y=0(y<4或y≥1).

5 求二次曲线Γ的切线方程

5.1 求过某定点P(x0,y0)的二次曲线Γ的切线方程

例6过点P(-1,2)作抛物线y2=2x的切线，求此切线方程.

5.2 求二次曲线Γ的斜率(或倾斜角)已知的切线方程

例7求二次曲线ax2+by2=1，(a>0，b≠0)倾斜角为α的切线方程.

6 结论

通过上文分析讨论，我们发现应用直线方程的参数形式能较好地解决直线与二次曲线位置关系的判断、直线与二次曲线交点、弦长、弦中点、切线等系列问题，并能避免繁杂的运算，拓宽学生视野.