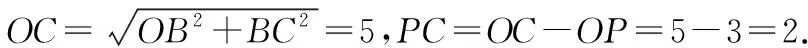省时省力的辅助圆
山东省滕州市滕南中学 郭效萍
1 引言
圆是初中阶段学习的重要图形,它的一些性质,例如,同弧所对的圆周角相等,半圆所对的圆周角是直角,直径是圆中最长的弦等,给解决问题带来极大的方便.在解答有关几何问题时,并不是图形中出现圆才利用圆的性质,有时需要构造一个辅助圆,然后利用圆的性质解答,这是解决几何问题的基本方法之一.
2 利用圆的集合定义构造辅助圆
从集合的角度定义:圆是平面内到定点距离等于定长的点的集合.根据这个定义可以得到,当几个点到同一点的距离相等时,则这几点一定在同一个圆上.这样构造辅助圆,解答时不仅能利用题中的已知条件,而且可以利用圆的一些性质.
例1如图1,在四边形ABCD中,AB=AC=AD,若∠BAC=25°,∠CAD=75°,分别求∠BDC和∠DBC的度数.
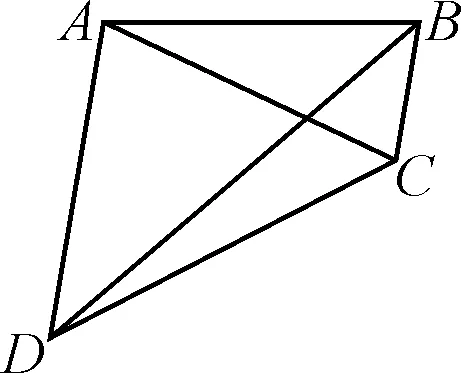
图1
解法1:(普通方法)
∵AB=AC=AD,
∴∠ADB=∠ABD,
∠ACB=∠ABC,
∠ADC=∠ACD.
∵∠BAC=25°,∠CAD=75°,
∴∠ACB=(180°-25°)÷2=77.5°,
∠DAB=∠DAC+∠CAB=100°,
∠ADC=∠ACD=(180°-75°)÷2=52.5°.
∴∠ADB=(180°-100°)÷2=40°.
∴∠BDC=∠ADC-∠ADB
=52.5°-40°=12.5°,
∠DCB=∠DCA+∠ACB
=52.5°+77.5°=130°.
∴∠DBC=180°-∠DCB-∠BDC
=180°-130°-12.5°=37.5°.
解法2:(构造辅助圆的方法)
由AB=AC=AD,得点B,C,D在以A为圆心,以AD为半径的圆上,如图2.
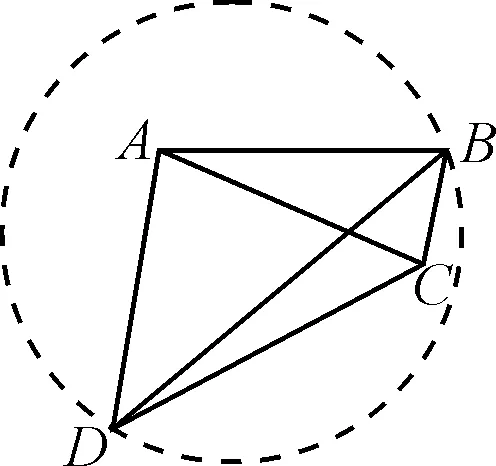
图2
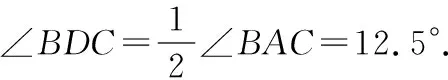
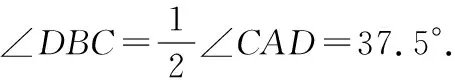
点评:比较上面两种方法可以发现,构造辅助圆后,解决过程明显简洁.这里主要利用了圆周角定理及其推论:同弧所对的圆周角相等,等弧所对的圆周角也相等.这是因为这些圆周角都等于它所对的圆心角的一半.
3 利用圆周角定理的推论构造辅助圆
因为90°的圆周角所对的弦是直径,所以当直角三角形的斜边一定时,直角顶点一定在以斜边为直径的圆上运动.此时构造辅助圆,可以确定直角顶点的运动轨迹.
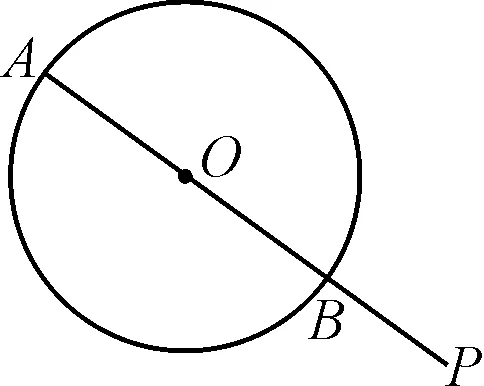
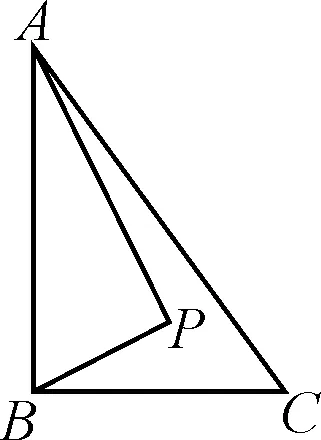
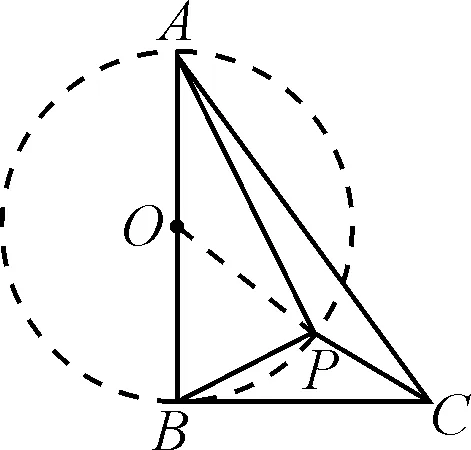
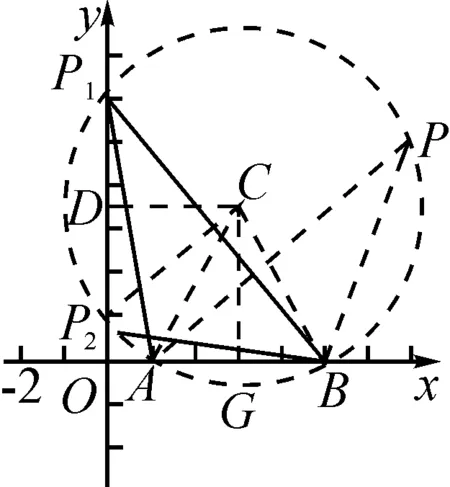
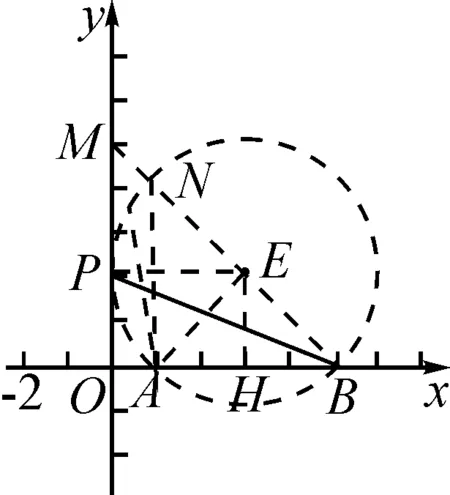
例2如图3所示,矩形ABCG(AB 图3 解析:如图4所示,根据90°的圆周角所对的弦是直径,当∠APE为直角时,点P应在以AE为直径的⊙O上.又因为点B,C,D在同一条直线上,∠APE的顶点P在线段BD上移动,所以点P就是⊙O与BD的交点.由图4可知,BD与⊙O有2个交点.故答案为:2. 图4 点评:本题确定点的方法使用的是交轨法,即从每一个条件出发确定一个点的轨迹,两个点的轨迹的交点就是符合题意的点.本题两个点的轨迹分别是一条直线和一个圆. 当一个角对固定长度的线段所张开的角度为定值时,角的顶点的运动轨迹为一个圆,此时可以作辅助圆,这条定线段为辅助圆的弦,这个角为圆周角.此时可以利用圆的相关性质解答问题. 例3如图5,点A与点B的坐标分别是(1,0),(5,0),点P是该直角坐标系内的一个动点. 图5 (1)使∠APB=30°的点P有________个. (2)若点P在y轴上,且∠APB=30°,求满足条件的点P的坐标. (3)当点P在y轴上移动时,∠APB是否有最大值?若有,求点P的坐标,并说明此时∠APB最大的理由;若没有,请说明理由. 图6 (2)①当点P在y轴的正半轴上时,过点C作CG⊥AB,垂足为点G,如图6. 由点A(1,0),B(5,0),得OA=1,OB=5,则AB=4. 则OG=OA+AG=3. 过点C作CD垂直于y轴,垂足为点D,连接CP2,如图6. 由点P1,P2是⊙C与y轴的交点,得∠AP1B=∠AP2B=30°. (3)如图7,当过点A,B的⊙E与y轴相切于点P时,∠APB最大.理由: 图7 可证∠APB=∠AEH,当∠APB最大时,∠AEH最大. ①当点P在y轴的正半轴上时,连接EA,作EH⊥x轴,垂足为点H,如图7. 由⊙E与y轴相切于点P,得PE⊥OP. 由EH⊥AB,OP⊥OH,得∠EPO=∠POH=∠EHO=90°. 则四边形OPEH是矩形,OP=EH,PE=OH=3,得EA=3. 圆外一定点与圆上各点连接而成的所有线段中,有一条最短线段和最长线段,这两条线段都在过圆心与圆外一点的直线上,如图8所示,最长线段是PA,最短线段是PB.利用这一点,可以求与圆有关的线段的最值. 图8 例4如图9,Rt△ABC中,AB⊥BC,AB=6,BC=4,P是△ABC内部的一个动点,且满足∠PAB=∠PBC,则线段CP长的最小值为________. 图9 解析:如图10,由∠ABC=90°,得∠ABP+∠PBC=90°.又∠PAB=∠PBC,则∠BAP+∠ABP=90°,即∠APB=90°,则点P在以AB为直径的⊙O上.连接OC交⊙O于点P,此时PC最小. 图10 点评:几何中求最值的情况包括:(1)利用轴对称求线段和的最小值;(2)利用勾股定理求曲面上或不同平面上两点之间的最短距离;(3)利用三角形相似解决系数不为1的线段和最小值问题;(4)利用直径是圆中最长的弦解决与圆有关的线段的最值. 几何问题中作辅助线的方法比较多,如作垂线、平行线、连接、延长、倍长中线、旋转三角形等,但作辅助圆这种作铺助线的方法容易被忽略.上述四个实例分别从四个不同的角度阐释了在什么情况下需要作辅助圆,如何作辅助圆,作辅助圆后如何利用辅助圆,以期对学生突破几何学习有所帮助.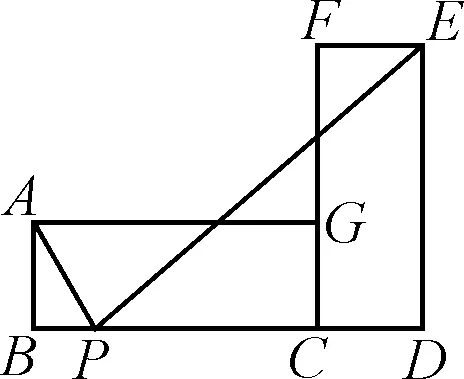
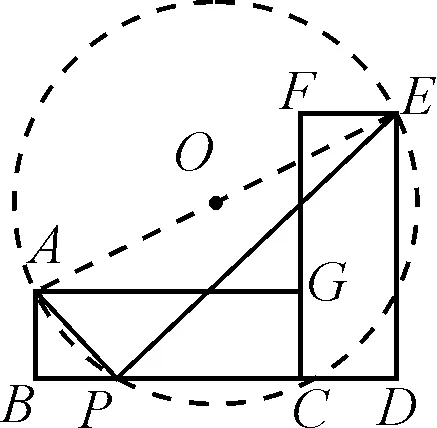
4 利用一个角对定线段所张的角度为定值构造辅助圆
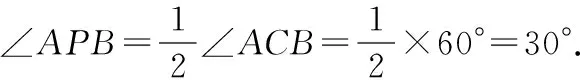
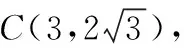
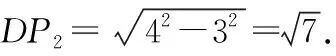
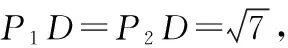
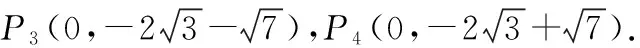
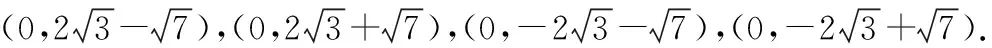
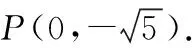
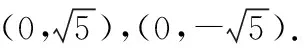
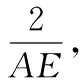
5 利用作辅助圆求最值