“双减”背景下初中数学作业设计的策略研究
——以二次函数为例
西华师范大学 张玮芳
1 引言
“双减”政策要求中学生的课下作业时间总量不超过一个半小时,而对于数学作业,时间应在 20 分钟左右,这就要求教师所布置的课后作业要“少量高效”[1].但现阶段很多老师依旧按照传统的方式布置作业,盲目地留大量的习题,推行“题海战术”,结果却不尽如人意,学生不仅没有熟练地掌握所学知识,还增加许多负担.那么如何提高数学作业设计质量,使学生“减负高效”地掌握所学知识,是笔者主要思考的问题.现就该问题提出一些策略.
2 充分了解学生,加强作业题目间的联系
想让学生通过作业高效巩固课堂所学的新知识,教师必须充分了解学生,针对学生普遍不熟练的知识布置作业,做到“对症下药”.教师要在课前、课中、课后积极地与学生沟通,得到切实有效的反馈.学生知识的掌握程度如何,哪部分知识薄弱难以理解等,这些都要做到心中有数.布置作业时,题目不能东拼西凑,要注意加强题目间的联系.比如,对于学生来说,二次函数的最值问题一直较难,这时我们要选取多个从不同角度考查二次函数最值问题的习题.顺序要由易到难,由简到繁,尽量让每道题都有前几题的思路或者结论作为基础,让学生边解题边思考,像上台阶一样循序渐进地掌握知识.

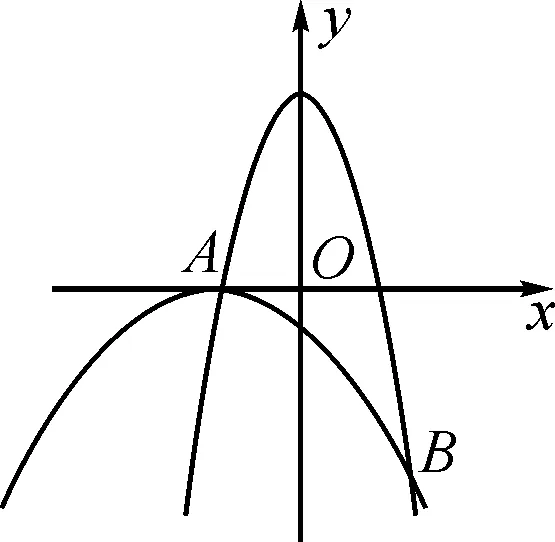
图1
作业2如图2,开口向下的抛物线与x轴交于点A(-1,0),B(2,0),与y轴交于点C(0,4),点P是抛物线上的一点,且位于第一象限,求四边形CABP面积的最大值.

图2
分析:这两道题目都属于二次函数的最值问题,题目之间看似独立却又相互联系.第一题求的是三角形ABC面积的最值问题,通过C,D在抛物线上,设出点C,D的坐标,得到线段CD(长度)的表达式,求出CD的最大值,进而求出三角形ABC的面积.第二题所用思想方法与第一题相同,但本题涉及到四边形CABP面积如何表达的问题,将四边形CABP合理分割后,其面积可以表达为三个三角形面积之和,再通过设点的坐标求出四边形面积的最值.综上所述,这两道题的联系十分紧密,所用到的数学思维方式贯穿始终,由三角形的面积最值扩展到四边形的面积最值.可见第一题为第二题的解答打下基础,整个过程循序渐进,对学生的要求也越来越高.经历这样的过程,学生将学会在解题中思考,不断进步,从而达到较高水平.
3 合理分组,加强作业的针对性
每个学生都是独立的个体,对于每一章的知识都有自己薄弱的环节,要想从根本上提高学习成绩,必须将这些薄弱环节都逐个击破,而合理分组可以针对性地帮助学生解决问题[2].例如,对于二次函数的作业,教师可以依据不同的知识点将练习题进行分组,如:A组重点是二次函数的定义及性质;B组重点是一元二次方程与二次函数的关系;C组重点是生活中的二次函数.同时,学生根据自己的学习状况自由选择其中一组或多组作业进行练习,这样就加强了数学作业的针对性.教师也可以依据难度将题目进行分组,基础较差的同学选择难度较小的题目,基础较好的同学选择难度较大的题目.总之教师可以依据自己班级的实际情况,对题目或者学生进行合理的分组.这样在一定程度上保证了学生作业的个性化,增强了作业的针对性,有助于提高学生的学习成绩,同时教师的任务也不会过于繁琐.
作业3A组:已知函数y=(m+3)xm2+4m-3+5是关于x的二次函数.
(1)若该函数的图象开口向上,求m的值;
(2)若该函数有最大值,求m的值.
B组:如图3,函数y=ax2+bx+c(a≠0)的对称轴为直线x=2,若x1,x2是一元二次方程ax2+bx+c=0的两个根,且x1 图3 A.x1+x2<0 B.4 C.b2-4ac<0 D.ab>0 C组:A,B两地生产同一品种的苹果,共100箱.A地生产苹果的总成本y(单位:元)与苹果数量x(单位:箱)之间存在函数关系y=ax2+bx,当x=10时,y=400;当x=20时,y=1 000.B地生产苹果的每箱成本为70元.从A地把该苹果运往C,D两地的费用分别为m元/箱和3元/箱;从B地把该苹果运往C,D两地的费用分别为1元/箱和2元/箱.C地需要90箱,D地需要10箱,当A,B两地生产这批苹果的总成本的和最少时,写出A,B两地总运费的和的最小值. 分析:以上三题是依据知识点将题目进行分组,其中A组题目较为基础,学生只要充分理解二次函数的定义即可解题.B组题目难度有所增加,需要学生对二元一次方程与二次函数的关系有深刻认识,并能与图象相结合进行解题.C组题目难度更大一些,与现实生活相联系,需要学生具有一定的数学阅读能力,能从语言文字中抽象出数学问题,再通过相关知识进行解题.A,B,C三组题目难度是依次上升的,学生可以依据自己的能力自由选择,这样就增强了作业的针对性,有利于巩固学生相对薄弱的知识点,增强学生自信心. 对于数学的学习,及时总结与复习是相当重要的.经过一阶段的学习后,教师应有计划地设置专题性数学作业.这里的专题作业主要指两类,一是根据题目涉及的数学思想方法分为不同的专题,二是将每一阶段所学的知识进行汇总形成不同的专题[3].对于第一类,教师可以根据每道题涉及的数学思想方法进行分类,例如,数形结合思想专题性作业、化归思想专题性作业等等.对于第二类,教师可以将该段时间所学的知识进行梳理,总结出重难点、高频考点等,再通过这些知识点,筛选一些与之匹配的典型的、重点的习题组成一份专题性的数学作业.专题性作业不应该局限于一个单元,只要是有所关联的知识点,甚至是一些探究活动都可以组成专题,例如函数专题作业、平面几何专题作业等等.专题性数学作业也不局限于以上两类,教师可以根据学生的实际情况设置多样化的数学专题性作业.以二次函数为例,可设置如下数形结合思想专题性作业. 作业4已知抛物线y=ax2+bx+c经过A(2,0),B(3n-4,y1),C(5n+6,y2)三点,对称轴是x=1,关于x的方程ax2+bx+c=x有两个相等的实数根. (1)若n<-5,试比较y1与y2的大小; (2)若B,C两点在直线x=1的两侧,且y1>y2,求n的取值范围. 作业5平面直角坐标系xOy中,O为坐标原点,点C在y轴正半轴上运动,二次函数y=x2与过点C的直线交于A,B两点,且CB=3AC,P为CB的中点,设点P的坐标为(x,y)(x>0),写出y关于x的函数表达式. 分析:作业4和作业5解题过程中都要画图,利用数形结合思想解题.作业4中未知数较多,学生在画图过程中可能有些吃力,但只要充分理解题意,解题过程并不复杂.作业5作图相对简单,但需要学生具有一定的几何基础,将代数知识与几何知识相结合才能解题,在此过程中,学生将体会到代数与几何的密切联系,感受到数学严谨的美. 教师应该充分认识到作业对于发展学生数学能力的重要作用.运用恰当的策略布置作业,以保证作业的科学性、题型的多样性.设计出内涵丰富、具有个性的作业.切实地锻炼学生数学思维,提升数学素养.让学生在完成作业的过程中感受到数学逻辑的严谨性,数学的美,从而发展学生的数学才能.同时,教师布置作业一定要以学生为本,关注学生的成长,关注学生数学思维的培养和数学能力的提升;布置作业要遵循循序渐进的原则,扎扎实实地帮助学生巩固课堂所学的知识,让每个学生都能从作业中体会到学习数学的成就感,培养数学学习的信心.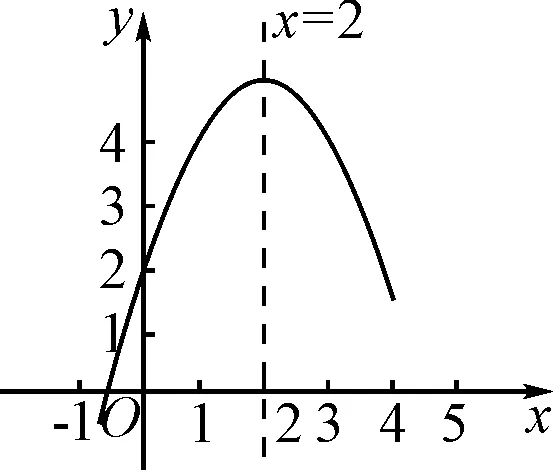
4 及时总结,设置专题性作业
5 结论

