践行深度学习 提高核心素养

苏州高新区实验初级中学 康 聪

1 引言

数学教育家波利亚指出：“教学生思考”意味着数学教师不只是传授知识，还应该努力发展学生运用所学知识的能力.数学教育从关注“基础知识”“基本技能”和“基本思想方法”的“三基”，转向了“四基”，开始重视学生学习数学的“基本活动经验”，这无疑对教师的课堂教学水平提出更高的要求.

提高学生的核心素养是一个长期的过程.在教学中，教师需要精心设计课程，研讨具有研究价值的问题供学生参与互动.本文采用苏教版教材，对教学内容的设计与改进提一点笔者的想法，以教学片断呈现，供读者参考.

2 “衔”——整合知识脉络，顺应思维发展

教学片段1：线段、射线、直线.

数学内容的学习是连续的，教师教学要注意学习内容的衔接，不能在初中阶段故步自封.线段和角是最简单的几何图形，是组成复杂图形的基本元素.学生在小学时已经学习过线段、射线、直线的相关内容，以旧知为立足点，抓住知识的来龙去脉，本节以苏教版七年级上册第6章“平面图形的认识(一)”的第一节“线段、射线、直线”为例.

师：相信同学们对这个课题并不陌生，在小学里，你学习过相关的哪些内容呢？

生1：线段有两个端点，有固定长度，可以测量；射线有一个端点，可以向一边无限延长；直线没有端点，可以向两边无限延长.

师：(在黑板上板书)延长与延伸.直线向两边具有无限延长的特点，直线无限延长是直线的特性，称之为直线的无限延伸性.也就是说，直线能够向两边无限延伸，射线向一边无限延伸.

刚才同学们讲，线段有两个端点，射线有一个端点，直线没有端点.(图1展示小学教材对应的内容.)

好，同学们说线段是可以测量的，说明线段有什么性质？

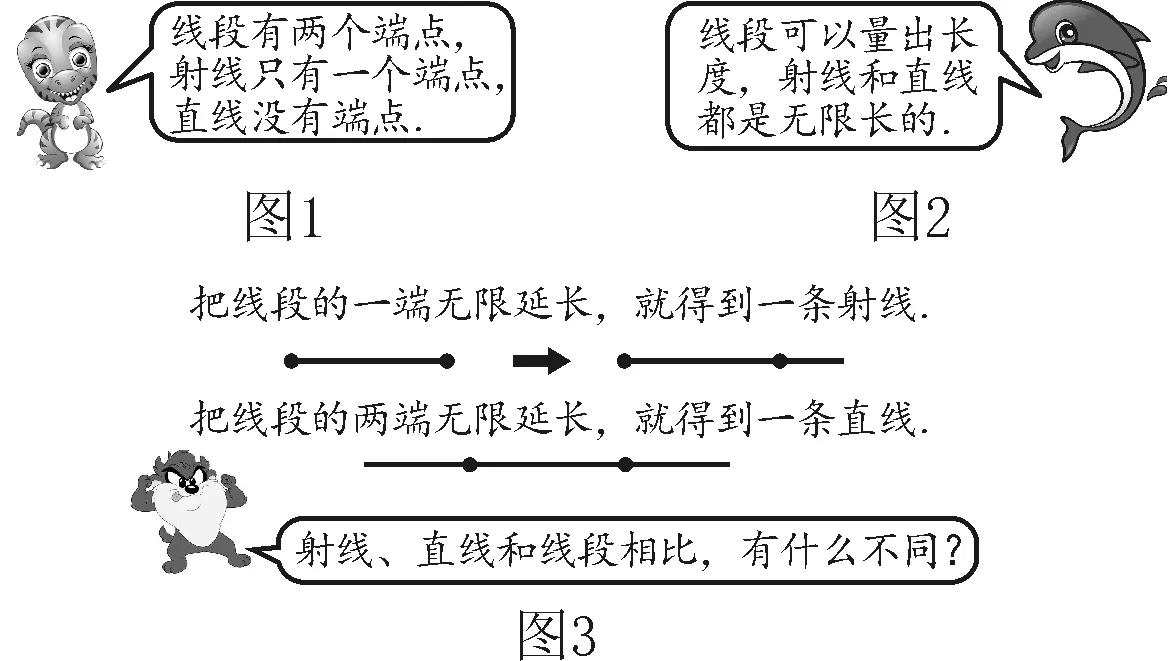
生2：可度量性.

生3：线段具有度量性，直线和射线没有可度量性.

师：很好！(教师展示小学教材对应内容，如图2.)

师：请同学们说明，线段、射线、直线有什么联系呢？

生4：把线段AB延着AB方向无限延长，得到射线AB；同样地，延长线段BA，得到射线BA；线段AB两端都延长，得到直线AB.(图3展示小学教材对应的内容.)

师：追本溯源，这是我们小学四年级的内容(PPT展示图4).

图4

教学说明：通过对小学中零散知识点的整合规范，师生互动，把“线”的区别与联系的内容整理出来，实现教学活动有效性的提升.在“问题”的提出中，教师直接进入课程重点，本章是苏教版七年级上册“基本平面图形”的起始课，是几何入门的第一节课，同时让学生领会几何内容学习要经历的“定义—表示—大小—线段和差”的抽象过程，体现整个知识发生、发展过程的完整性.

3 “探”——从式到形，拓展思维的局限

教学片段2：反比例函数的图象与性质(1).

在整个初高中学习系统中，解析几何始终是学生学习的难点.“以形看数”和“以数解形”等数与形的结合思想，需要教师教学设置层层递进的教学难度，也是教学目标中基本思想与基本活动经验积累的重要任务.下面以八年级下册第11章第二节“反比例函数的图象和性质(1)”的教学片段为例.

生1：图象上的点的横纵坐标的符号相同.

师追问：说说你是怎样分析的呢？

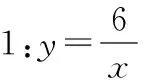
生2：x≠0，因为分母不能为0.

师：如果x，y不能取到0，说明函数图象会有什么特点呢？

生3：x≠0，图象与y轴没有交点；同样地，y≠0，图象与x轴没有交点.如果都取不到0，说明图象与坐标轴没有交点.

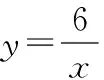
生4：增减性.y随x的增大而减小.

具体地说，当x>0时，x越大，y越小；当x<0时，x越大，y越小.

师追问：你是怎样抽象得到的呢？现在我们要具体化，例如当x>0时，举例子说明.

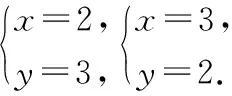
教师引导(操作画图)：当x>0时，y随x的增大而减小.

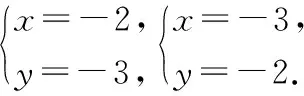
师：如果不讨论x的范围，从整体看，可不可以这样描述呢？

师：非常好，请同学总结下增减性的生成过程.

生6：要具体强调在哪个象限，当x>0时，y随x的增大而减小；当x<0时，y随x的增大而减小.

师：很好，增减性一定要强调在哪个象限！

教学说明：教师引导学习函数的一般路径，利用函数表达式分析两个变量之间的符号关系，从“数”想“形”，探究出函数图象的位置，分布在哪一个象限，进而在不同象限内，得到函数图象的性质.在整节课中，学生自主探究，在平面直角坐标系中，对函数图象的结构进行研究，包括取值情况与图象分布；教师适当引导，从“模糊”走向“精确”，带领学生初步感知图象的分布区域和走向，利于学生思维的培养和能力的提升，从而确定函数本身的性质.

4 “归”——巩固知识元之间的联系

教学片段3：直线与圆的位置关系(1).

教学是循序渐进的过程，教师要教的不仅仅是知识，更重要的是要教会学生如何思考以及解决问题的能力.在本节课前，学生已经学习过点与圆的位置关系，用圆心到定点的距离d与半径r的大小来定义，而圆心到点的距离d是点与点之间的最近距离，即“两点之间线段最短”.由此，直线与圆的位置关系可以怎样判定呢，我们如何利用划归的思想解决新的难题？[本节是九年级上册第2章第5节“直线与圆的位置关系(1)”].

师：请同学们用圆规在操作纸上画出一个圆，再将一把直尺在纸上平移.如果把直尺的边缘看作一条直线，那么在直尺平移的过程中，请把直线与圆的位置关系画出来.

(教师通过学生画出的图形，展示出以下三种情况.)

现在，如何来描述直线与圆的位置关系呢？

生1：通过直线与圆公共点的个数来描述，图5没有公共点，图6有一个公共点，图7有两个公共点.

图5

图6

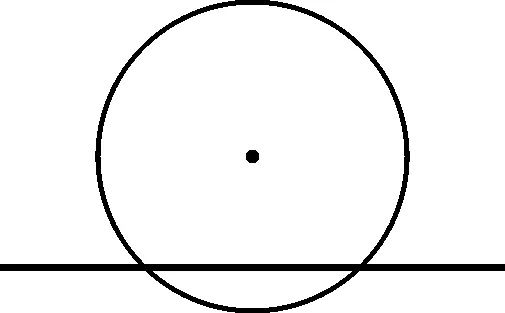
图7

师：很好，观察图形，我们发现，图5中直线与圆没有公共点，也就是直线上所有的点都在圆外；图6是直线上有一个点在圆上，其他点在圆外；图7是直线上有两个点在圆上，其余的点在圆外.我们按照直线与圆的公共点个数，来定义直线与圆的位置关系：

直线与圆有两个公共点时，叫做直线与圆相交；(如图7)

直线与圆有唯一公共点时，叫做直线与圆相切；(如图6)

直线与圆没有公共点时，叫做直线与圆相离.(如图5)

我们知道，点与圆的位置关系，可以用d与r的大小关系进行衡量，那么，同学们是否可以用类比的思想，在直线与圆的位置关系中，也用一组对应的量来进行比较呢？

生2：可以找到直线上的点到圆心的距离与半径r进行比较.

师：好的，请举一个实例.

生2：例如图8，直线上的所有点与圆心的距离都大于r.

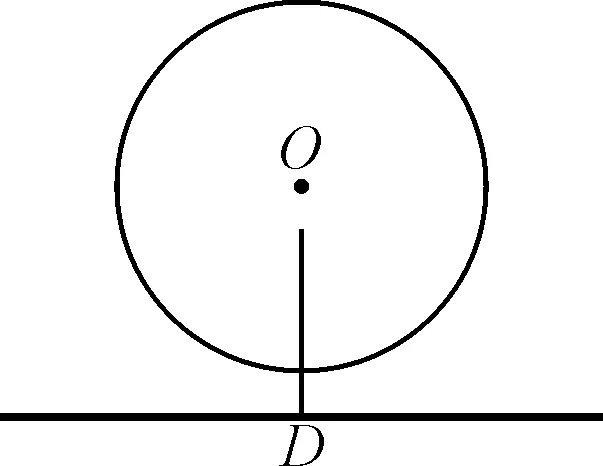
图8

追问：直线上有多少个点？

生(齐说)：无数个点.

师：既然有无数个点，你是否能找出一个有代表性的点刻画与圆心距离大小的情况.关键是要找到什么呢？

生3：要找到圆心到直线的最近距离.

师追问：何时最短呢？

生4：垂线段最短.也就是，直线外一点到直线的最近距离，是过圆心向直线作垂线段(如图8).

师：如图8，也就是与哪个量之间的比较？

生5：也就是圆心O到直线的垂线段OD与r的大小比较.

师：这样类比，我们找到了直线与圆的位置关系的数对，圆心到直线的距离d与r的大小比较.请同学们依次说出相离、相切、相交三种位置关系中，d与r的大小情况.

生6：相离⟺d>r；相切⟺d=r；相交⟺d

教学说明：这一环节具有思维的挑战性，难点是引出圆心到直线的距离d.直接教学生作出图形并不难，而学生对点与圆的位置关系认识并不深刻.点与圆位置关系的拓展，使得学生对直线与圆的位置关系的认识越来越深刻，课与课、节与节的连贯性，让学生进入深度思考，促进数学核心素养的落实.

5 结束语

深度学习的目标是希望学生在基本数学知识学习的过程中，自主挖掘相关知识的联系，深度理解数学本质，最终由“学会”变成“会学”.教师在课程设计中，要基于学生的学习和思维，重视对数学必备知识与关键能力的深度理解，立足教材，活用教材，多方位多角度思考，构建知识间的联系与转化，促进知识的融合，给学生实现深度学习创造良好的条件.在教学过程中，引导学生用数学的眼光观察、分析问题，并学会用数学语言表达问题，是我们数学核心素养贯穿成功的最主要的标志.