透析本质 巧构解题——例谈通过解题深化学生数学素养

■ 武汉第三寄宿中学 陈曼玲

在几何图形中设置动点，探究动点的轨迹，从而研究某些几何量之间的关系，这类因动点而产生的最值问题是初中数学教学的热点和难点。通过对这类问题的分析解决，可以帮助学生夯实基础知识和基本方法，培养学生推理论证等逻辑思维能力，透过表象认清数学本质，巧妙建构模型解决问题。

一、典例呈现，提出问题

（2021年武汉市中考16题）如图（1），在△ABC中，AB＝AC，∠BAC＝90°，边AB上的点D从顶点A出发，向顶点B运动，同时，边BC上的点E从顶点B出发，向顶点C运动，D，E两点运动速度的大小相等，设x＝AD，y＝AE+CD，y关于x的函数图象如图（2），图象过点（0，2），则图象最低点的横坐标是__________.

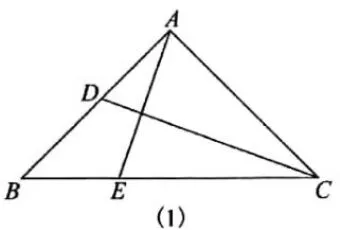
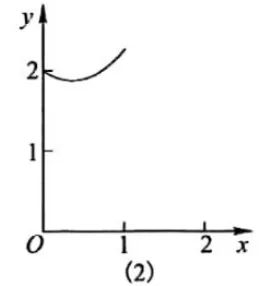
此题从题面上看，将几何中常见的的三角形图形与函数图象有机的结合在一起，构思新颖，让学生觉得似曾相识，一点也不陌生，很愿意去做，但真正做的时候却有点棘手，是又爱又怕喜忧参半!

二、数学建模，转化问题

通过阅读题目，知道在ΔABC中，D,E两动点在运动过程中满足AD=BE，由图象过点（0，2），可得出AB=AC=1，问题转化为当AD为何值时，AE+CD最小，即a+b型最值问题。在这类问题中，我们通常可以转化为“将军饮马”或者“三角形中三边的关系”来解决，从而找到问题的根本，剩下的就需要借助全等来进行线段的转化了。

三、透析本质，巧构解题

思路一：如图1，过点A做AF∥BC（或做∠FAB=450），且AF=AB,连FD,CF，即以AD为边补了一个角一条边，则可证ΔFAD≅ΔABE（SAS），得FD=AE，于是AE+CD就转化为CD+FD,当C,D,F三点共线时CD+DF最小，此时D点运动到G点，即求AG的长，只要解ΔAFG就可以了。在ΔAFG中，已知∠FAB=450，AF=1,可求 ∠AFG=22.50,ΔAFG可解，从而可得。

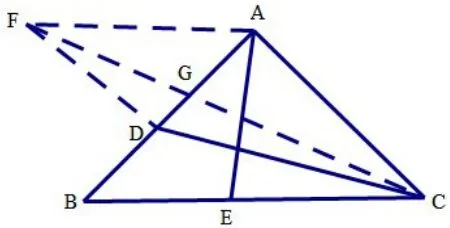
图1

思路小结：CD不动，将AE与CD转化到同一个三角形中，从而利用三角形三边之间的关系顺利找到最值。

思路二：如图2，过点B作BF⊥BE（或做∠EBF=900），且BF=AC,连EF,AF，即以BE为边补了一个角一条边，则可证ΔADC≅ΔBEF（SAS），得EF=DC，于是AE+CD就转化为AE+EF,当A,E,F三点共线时AE+EF最小，此时E点运动到G点，即求BG的长，只要解ΔBFG就可以了。在ΔBFG中，已知 ∠EBF=900，BF=1,可求 ∠AFB=22.50,ΔBFG可解，从而可得。

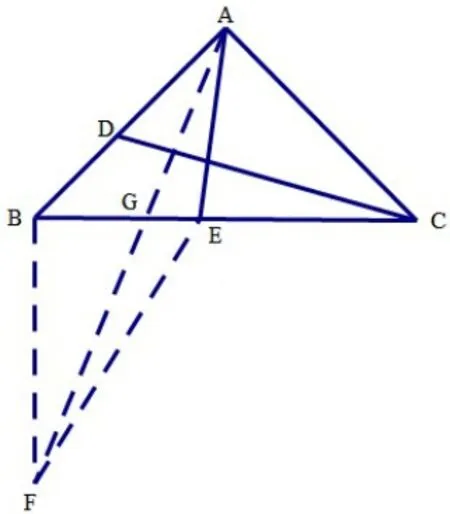
图2

思路小结：AE不动，将AE与CD转化到同一个三角形中，从而利用三角形三边之间的关系顺利找到最值。

思路三：如图3，过点A做∠DAF=450（或AF⊥BC，或取BC中点均可），且AF=AB，连DF，则可证ΔADF≅ΔBEA（SAS），得DF=AE，于是AE+CD就转化为DF+CD,问题转化为在AB上找一点D，使点D到两定点C,F的距离和最小，即学生熟悉的“将军饮马”问题，我们只需做点C（或点F）以直线AB对称轴的对称点H，连FH交AB于点G，则点D运动到点G时，求AG的长即可。做C,H关于直线AB对称，可得H,A,C三点共线，AB=AC=HA=AF=1，可证∠H=22.50，解RtΔHAG，可求。

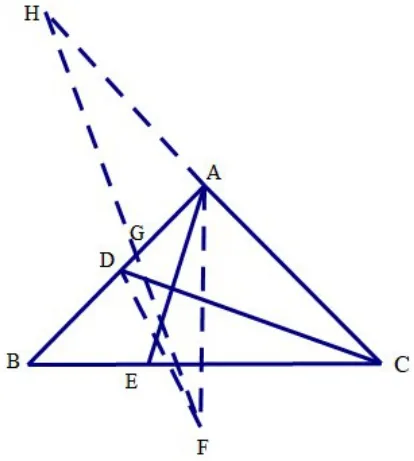
图3

思路四：如图4，过点B做∠EBH=900（或BH⊥BC），且BH=AC，连EH，则可证ΔDAC≅ΔEBH（SAS），得EH=DC，于是AE+CD就转化为AE+EH,问题转化为在BC上找一点E，使点E到两定点A,H的距离和最小，即学生熟悉的“将军饮马”问题，我们只需做点H（或点A）以直线BC对称轴的对称点F，连FA交BC于点G，则点E运动到点G时，求BG的长即可。做F,H关于直线BC对称，可得H,B,F三点共线，AB=AC=HB=BF=1，可证 ∠F=22.50，解RtΔBGF，可求。

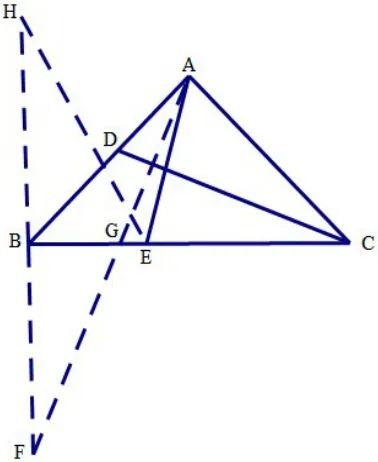
图4

思路小结：利用全等，将问题转化为将军饮马问题。

对于以上解法，我们在平时教学中对学生需多加引导和练习，找到技巧，学生自然会理解并熟能生巧，而此题的设计巧妙之极，不用繁琐的计算，只需静下心来思考，顿悟后犹如醍醐灌顶，豁然开朗，问题得到解决，学生能力显著提升。

四、深化拓展，提升素养

求a+b型最值方法：等线段全等转化对称法

1.以相等线段中的一条构造等角等边制造全等；

2.由全等把其中一条动线段a转移到b的另一侧；

3.当两定点在某一直线异侧时利用三角形三边之间的关系连接两定点得到一条线段该线段的长度即为a+b的最小值，当两定点在某一直线同侧时应用“将军饮马”模型解决a+b的最小值_________。

下面我们通过阶梯式的题目设计来实施模型的应用。

例1：AD为等边ΔABC的高，AB=6,E在AD上，F在AC上，且AE=CF，当BF+BE最小时，最小值为__________。

分析：此题比较简单，等线段条件分明，等线段所在的三角形直观明了，可直接运用模型构造求解。

在图5中，以AE为边作∠EAG=600,且AG=BC,则 ΔAEG≅ΔCFB(SAS),则EG=BF,求BE+BF的最值转化为BE+EG的最值即可，当B,E,G三点共线时，即E点运动到H点时BE+EG=BG最小。在RtΔBAG中，AB=AG=6，则即为BE+BF的最小值。

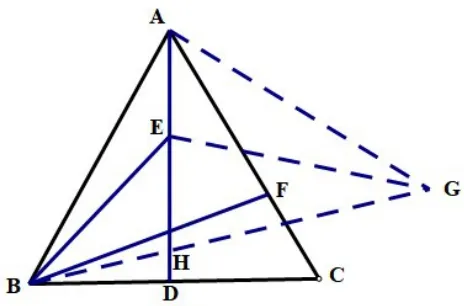
图5

在图6中，以CF为边作∠FCG=300,且CG=AB,则 ΔAEB≅ΔCFG(SAS),则FG=BE,求BE+BF的最值转化为FG+BF的最值即可，当B,F,G三点共线时，即F点运动到H点时FG+BF=BG最小。在RtΔBCG中，CB=CG=6，则即为BE+BF的最小值。

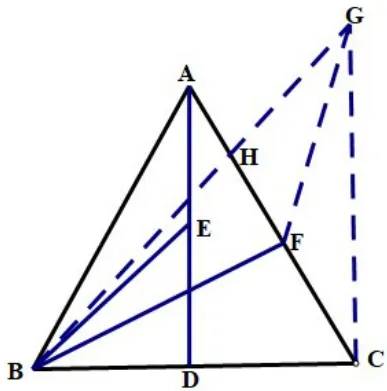
图6

在图7中，以AE为边作∠EAG=600,且AG=BC,则 ΔAEG≅ΔCFB(SAS),则EG=BF,求BE+BF的最值转化为BE+EG的最值即可，问题转化为在AD上找一点到两定点B,G的距离和最小，因为B,C关于直线AD对称，连接GC交AD于点H，即E点运动到H点时BE+EG=CG最小。在RtΔCAG中，AC=AG=6，则即为BE+BF的最小值。

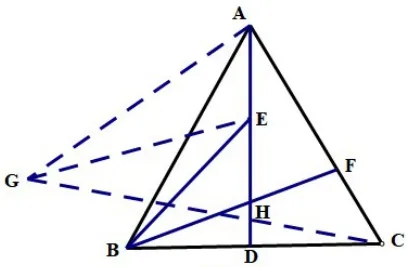
图7

在图8中，以CF为边作∠FCG=300,且CG=AB,则 ΔAEB≅ΔCFG(SAS),则FG=BE,求BE+BF的最值转化为FG+BF的最值即可，问题转化为在AC上找一点到两定点B,G的距离和最小，作B,P关于直线AC对称，连接GP交AC于点H，即F点运动到H点时BE+EG=GP最小。可求BE+BF的最小值为。,D是BC的中点，则四边形DMNC周长最小值为_______。（答案为）

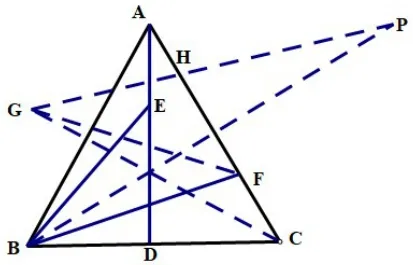
图8

上述四种方法中，图8所采取的方法在计算GP时较为复杂，建议采用另外三种方法。

本题还可以求CE+BF的最小值，方法不变。

例2：如图9,ΔABC中AC=BC=4,∠ACB=900,线段MN在边AB上运动，

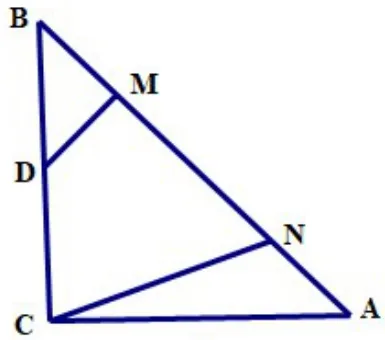
图9

分析：我们不难发现要运用上述模型，就需要找到等线段，可过点C作CE⊥AB（或取AB中点，或作∠ACB的角平分线）,得到，于是BM=EN，就可以运用模型构造了，下面画出四种构造的图形，分别见图10，图11，图12，图13，就不一一赘述了。

图10

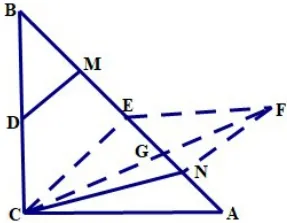
图11

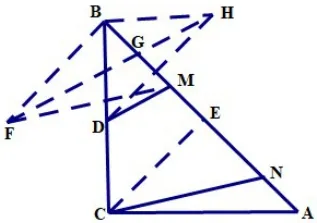
图12

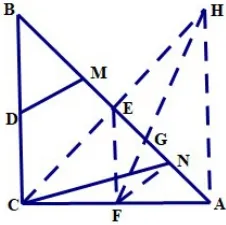
图13

五、总结反思，优化教学

1.基本知识点是解决几何问题的理论依据

书本上的基本知识点很多，根据问题有效的正确的运用相对应的基本知识，需要我们在平时的教学中不断的引导学生一方面熟悉基本知识，另一方面要在实际的练习中多加运用，举一反三，从而提高学生的数学素养。

2.找准关键条件是解决几何问题的突破口

题目中的显性条件运用很重要，但隐含条件推出的结论，才是突破几何题目的关键点，一道几何题的方法往往并不唯一，要善于捕捉题中的信息，找准关键便可做到一题多解，甚至多题一法。教师在日常的教学中要有目的地引领学生逐步学会，提高学生的能力。

3.进行常规思维训练是解决几何问题的基本

在上述问题中，注重常规思维训练，注重基本图形，常见辅助线的添加等常规经验积累尤为重要。课堂上，教师要让学生自己进行充分的探索，可能学生解决不了问题的全部，但当面对一道题时，常规的思维需要会很快达到，日复一日的坚持，相信学生能有效提高数学思维品质。

4.注重知识的生成过程是解决几何问题的核心

学生自己能做的，应当让学生自己去想，把教学重心转移到引导学生探索知识的产生，发展和形成上来，学生的发展实际上就是思维的发展，要提高学生解决问题的能力，教师就必须让学生经历问题解决的全部思维过程，才能使学生数学知识的掌握不仅仅知其然，而且知其所以然，因此，教师转变思想，给学生自由思考的空间，梳理知识系统，这才是符合学生长远发展的真正高效率的教学措施。

总之，初中数学可运用的模型很多，教师在平时的教学中要引领学生知晓方法，辨明变化，由知一理到通一片，积累解题经验，提升数学素养。