变速器齿轮微观修形对振动响应的影响研究
雷 刚,王虎银,刘子谦,姜艳军,陈超超,秦 凌
(1.重庆理工大学 车辆工程学院, 重庆 400054;2.重庆青山工业有限责任公司, 重庆 402761)
随着人们对汽车乘坐舒适性的提高,变速器的NVH(noise、vibration、harshness)性能表现越来越重要。汽车变速器作为动力传递的主要装置,其变速器齿轮系统的振动噪声主要由内部激励和外部激励共同引起,其中外部激励主要由发动机曲轴旋转的不平衡力及力矩、路面随机激励、齿轮系统转子不平衡、几何偏心、滚动轴承等引起;内部激励主要由齿轮系统时变啮合刚度激励、误差激励、啮入啮出冲击激励等引起。对于齿轮系统而言,纵使没有受到外部激励,变速器齿轮系统亦会受到内部激励从而引起振动噪声,针对齿轮内部激励引起的振动噪声问题,可以采用合理的齿轮微观修形以降低齿轮的传递误差,提高齿轮的承载能力,从而降低变速器的振动噪声。葛敏等[1]对于修形采用的是工程经验,彭卓凯等[2-3]通过接触斑点并采用正交试验设计得到齿轮的微观修形参数,结果显示通过合理的修形可以改善齿轮啸叫噪声。石怀瑞等[4]针对某DCT变速器的啸叫噪声,采用台架NVH试验和阶次分析,使用仿真分析手段确定齿轮微观修形参数,以此来降低齿轮的传递误差。岳会军等[5]采用有限元法进行内部激励分析,并且考虑在齿轮温度场的影响前提下,以传递误差波动量小,齿面接触状态良好为优选目标,经大量仿真结果对比,确定微观修形方案。王梦琪等[6]以单对齿轮为研究对象,设计单项不同的齿形和齿向的修行方案,通过对比单项修形的优化结果,制定6种综合修形方案,进行接触斑点云图的对比分析,证明采用合理修形可以有效的降低振动噪声。范孝良等[7]结合ISO的经验公式对齿轮进行微观修形参数的求解,以微观修形来降低传递误差,且通过测试壳体表面的响应节点来表明壳体表面响应降低,从而间接反应出NVH性能改善。石鹏飞[8]在Romax Designer中建立2 MW风电齿轮箱的刚柔耦合模型,结合微观修形理论通过多次实验调试,得出最优修形参数,分析了齿轮微观修形对传递误差、接触强度以及承载能力的影响。苏成云等[9]由于自动变速的单对齿轮参与多挡位动力传动,所以对齿轮进行了多目标多工况的设计研究,为变速器的多工况研究提供参考。苏成云等[10]采用Romax软件建立自动变速器模型,以传递误差为优化目标,研究齿向修形和齿形修形对变速器壳体的振动响应影响,并且进行灵敏度分析,便于加工制造。潘文华[11]针对齿轮啸叫问题,提出通过源头控制齿轮的宏观参数和微观参数,除此之外通过传递路径来进行控制;其中对于微观修行部分主要研究了齿形修形、齿向修形,即通过齿轮源头和传递路径很好的改善了变速器的啸叫问题。扈建龙[12]针对纯电汽车减速器的振动噪声,基于粒子群算法对齿轮修形参数进行多目标优化,获得帕累托最优解。可以看出以上的齿轮微观修形研究结果多数都是采用工程经验和经验公式进行修形,对于采用优化算法计算修形参数的研究较少。
本文在上述研究结果基础之上,采用2种修行方式,第一种是采用ISO经验公式和工程经验确定微观修形参数;第二种是基于遗传优化算法,将遗传算法应用到齿轮的微观修形的寻优中,同时考虑多个优化因素。将2种修形结果与未修形前的传递误差、承载能力进行对比研究,结果表明:2种修形均可以降低齿轮的传递误差,提高齿轮的承载能力,从而抑制齿轮的振动噪声发生。
1 基于Romax模型的建立
使用齿轮专业分析软件Romax建立该DCT变速器模型,为了减少仿真结果的误差,建立整个变速器的挡位模型,主要包括齿轮、轴、概念离合器、差速器、变速器总成壳体。使用Hypermesh对变速器箱体进行划分网格,再在Abaqus中进行有限元求解,将得到的有限元导入到Romax进行缩聚,完成刚柔耦合模型的建立,即箱体的刚度矩阵全部缩聚到各个轴承的中心位置,建立的仿真分析模型如图1所示。全文主要对3挡齿轮进行研究分析,3挡齿轮副相关参数如表1所示。分析中的负载扭矩为80 N·m,输入转速为3 000 r/min,计算得到的功率为45.23 kW。
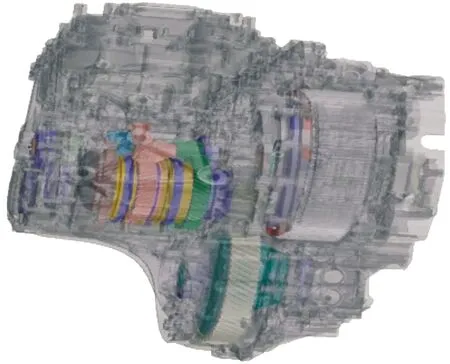
图1 变速器系统仿真分析模型示意图
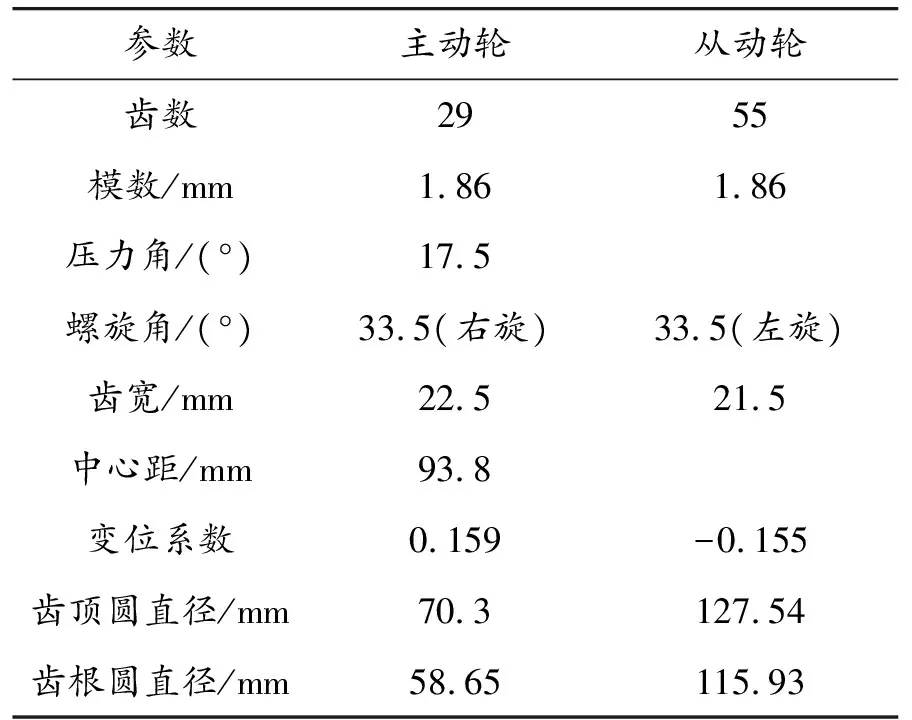
表1 3挡齿轮参数
2 微观修形介绍
2.1 齿形修形理论
齿形修形主要包括齿形鼓形量修形、齿形斜度修形、齿顶(齿根)修缘等,如图2所示。齿形修形主要是为了减少啮合冲击和载荷,改善基节误差和载荷分布[13-14]。其中,ISO 6336齿轮标准对于齿形修形量的推荐公式为:
(1)
式中:KA为某工况下的系数;Ft为齿轮切向力;B为齿宽;εα为齿轮端面重合度;Cγ为齿轮啮合综合刚度。
文献[9]给出的齿廓修形曲线为:
e=ek(x/l)b
(2)
式中:ek为最大修行量;x为啮合点坐标;b为齿廓修形曲线;l为界点至啮合起始点或者下界点至啮合终止点的距离。
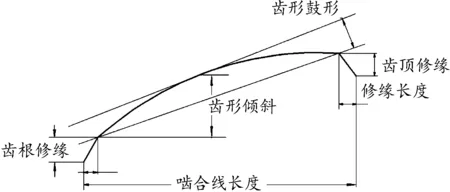
图2 齿形修形示意图
2.2 齿向修形理论
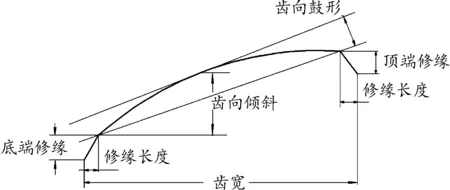
齿向修形包括齿向鼓形量修形、齿向斜度修形等,如图3所示,轮齿承受载荷后会发生弯曲、扭转变形,引起齿轮载荷分布不均,降低齿轮的承载能力。齿向鼓形量即沿齿宽方向的鼓形量,它的设计是保证齿轮发生变形后能够补偿轮齿齿向啮合的弹性变形。若考虑发生接触后的变形和齿向啮合误差,参照ISO 6336公式,则齿向鼓形量的计算公式为:
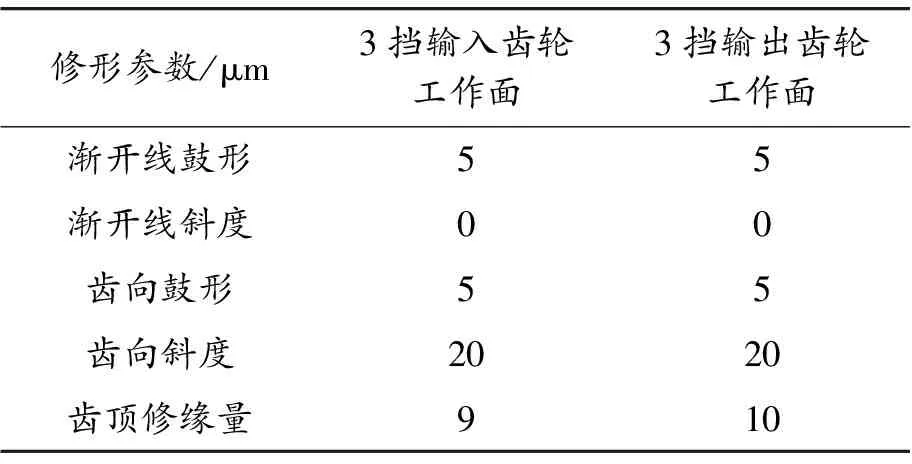
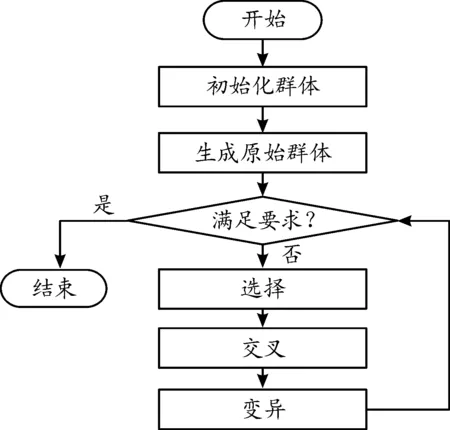
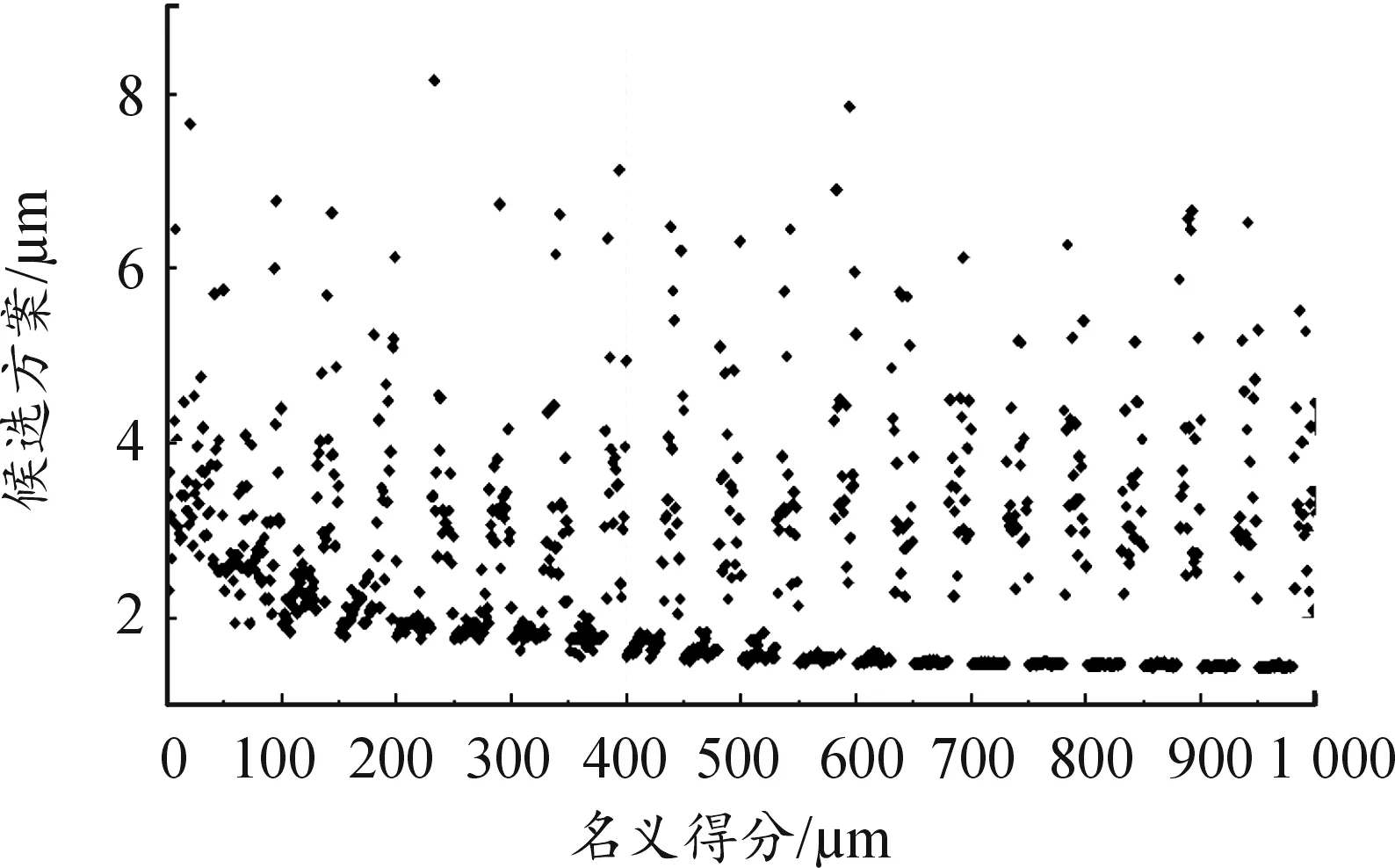
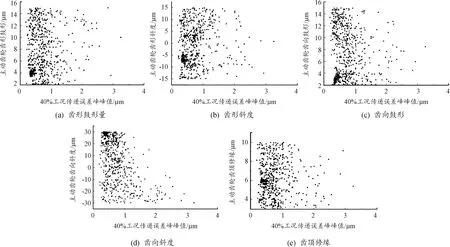
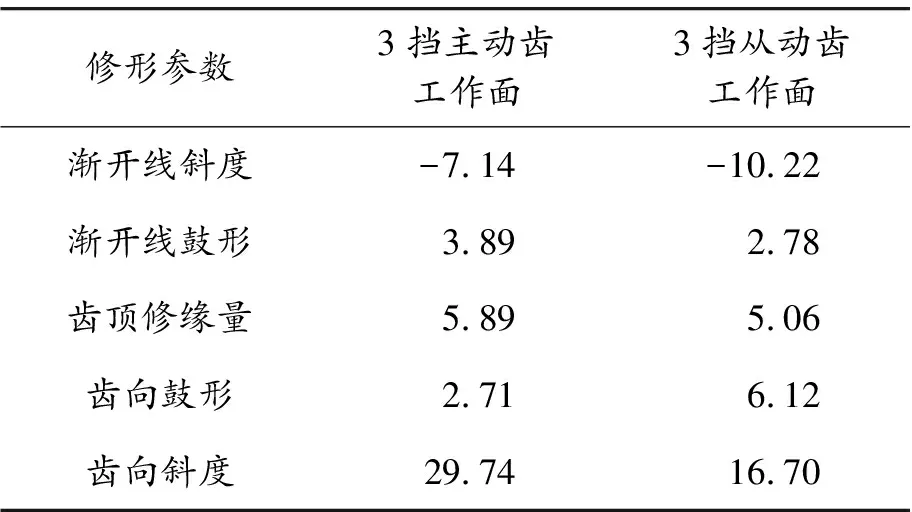
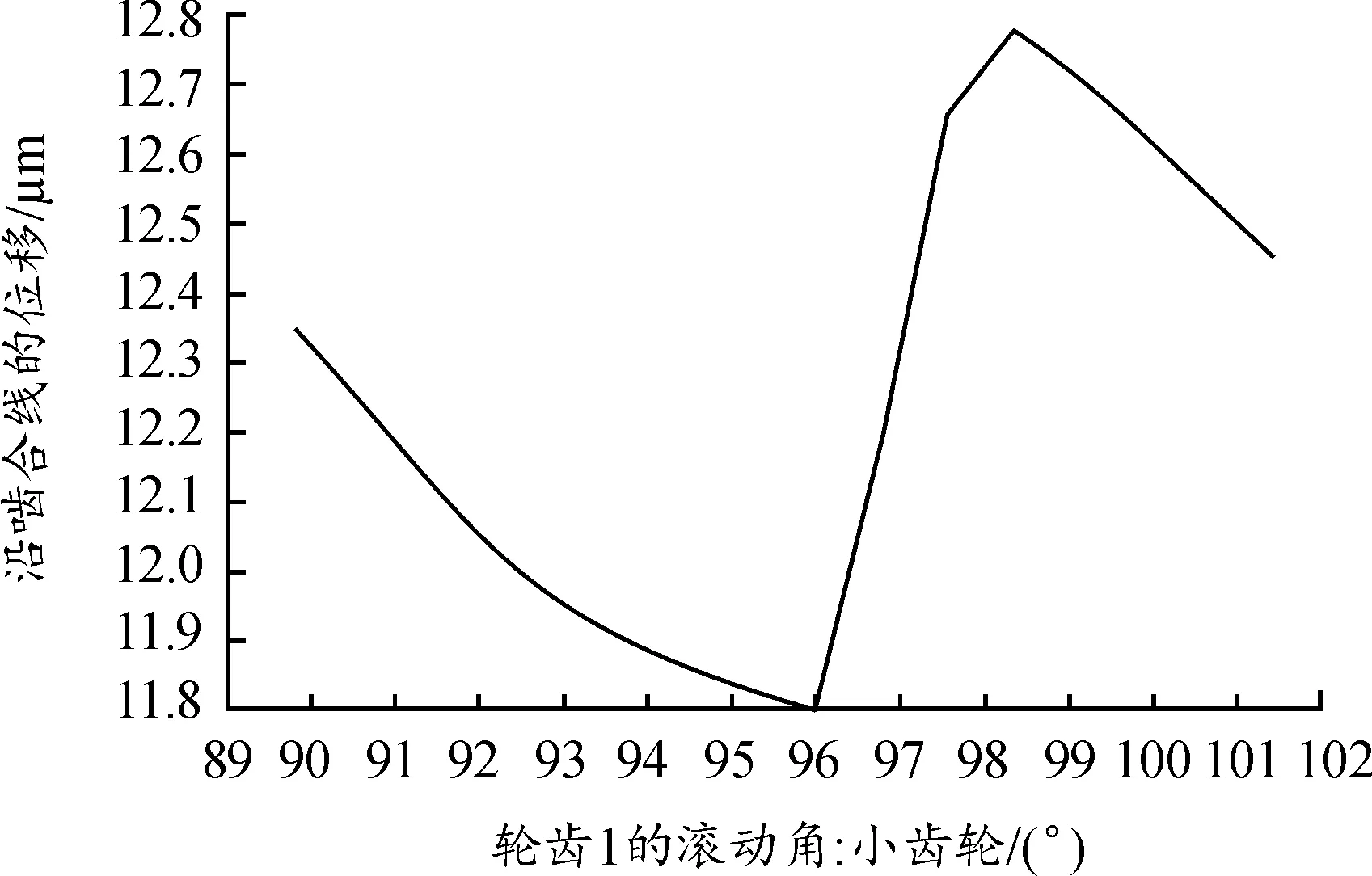
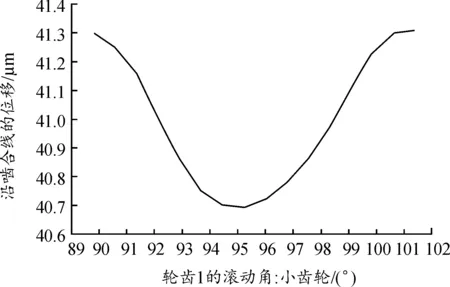
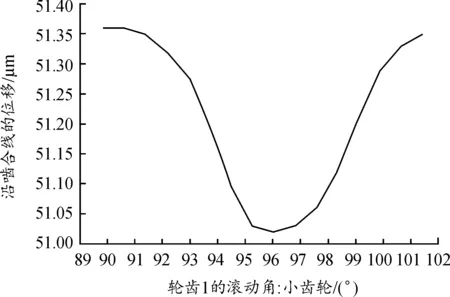
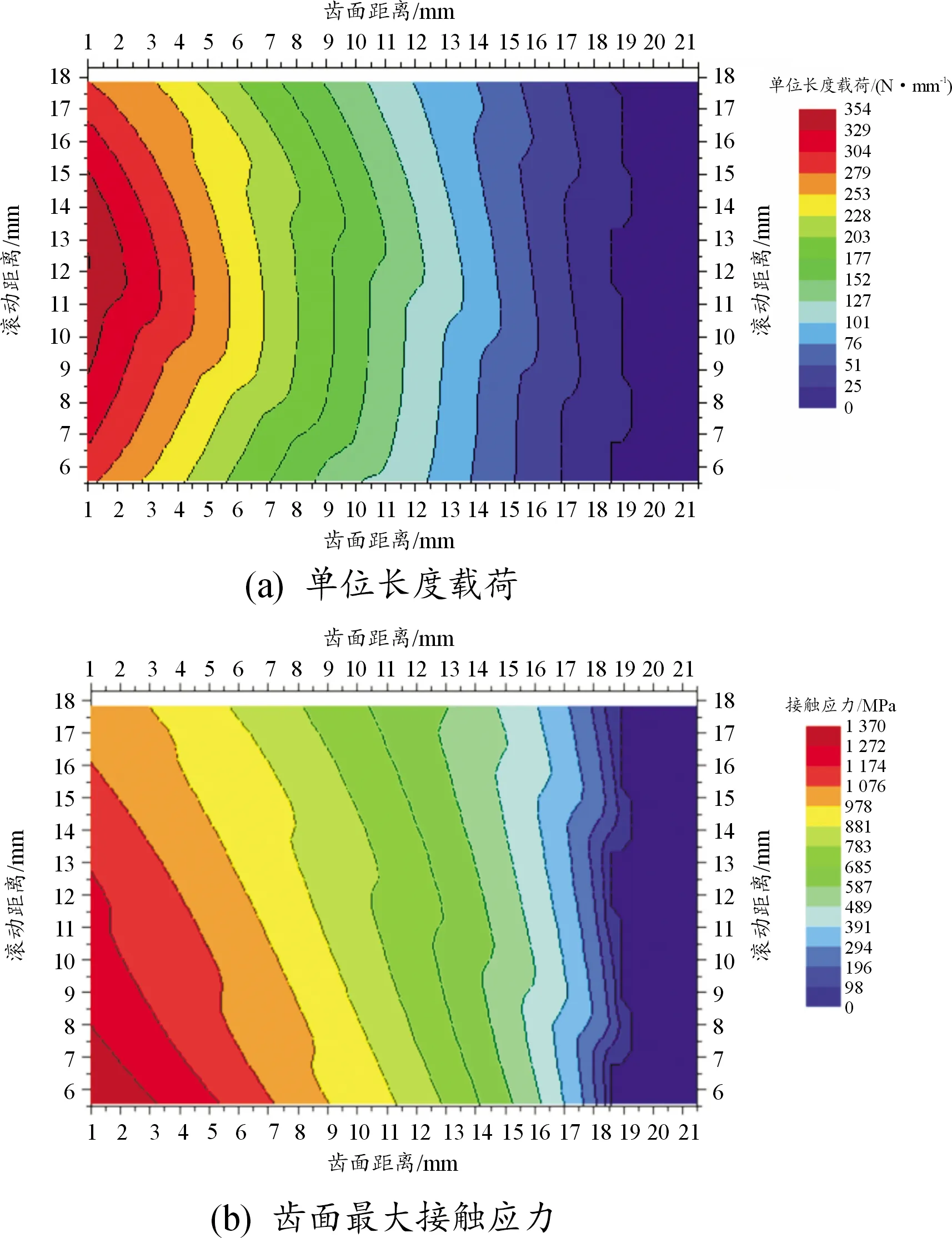
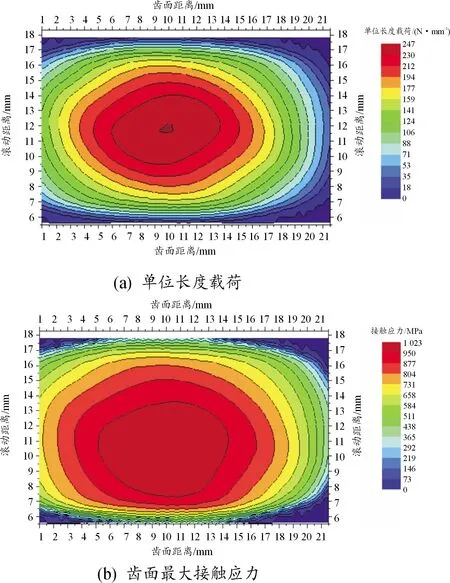
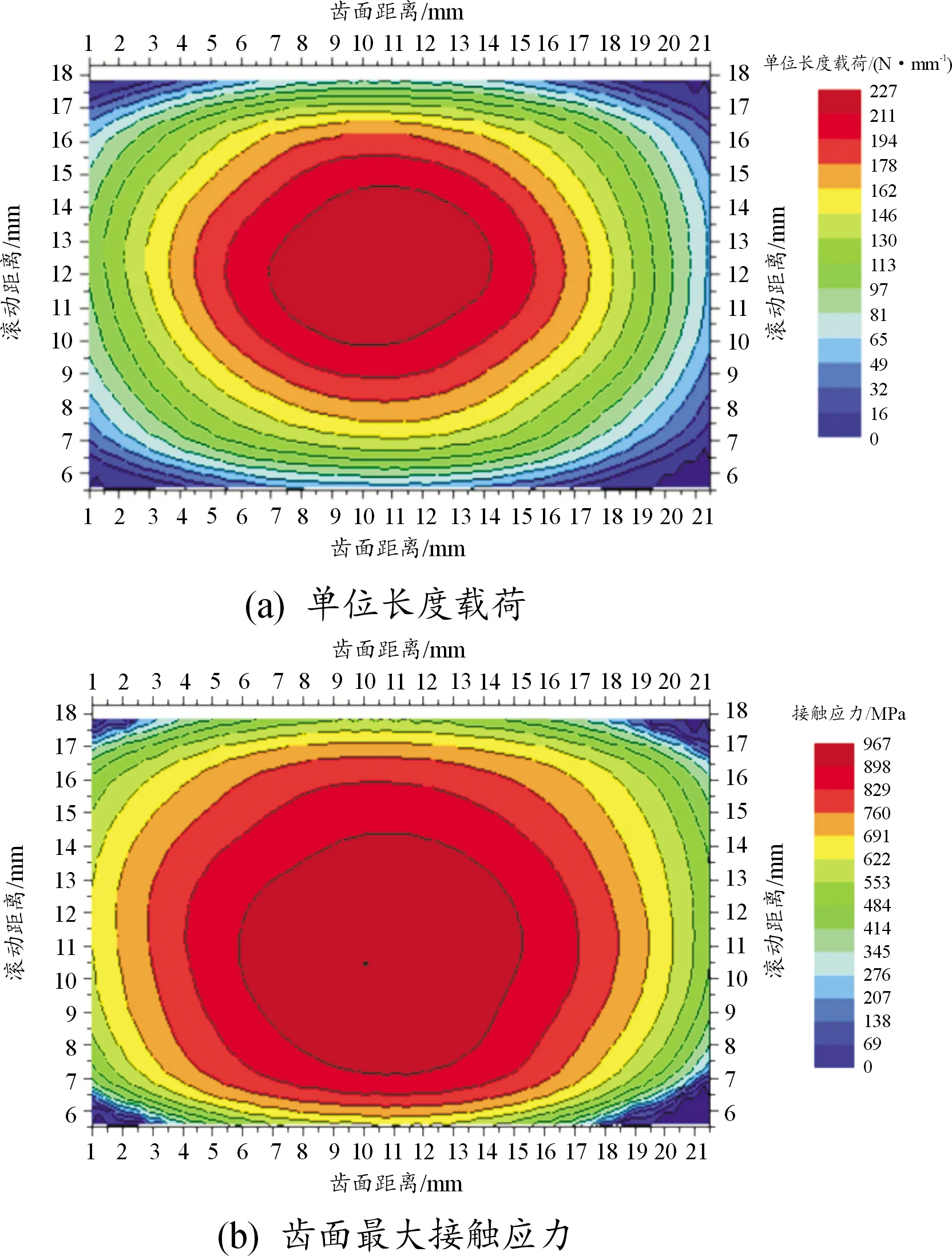
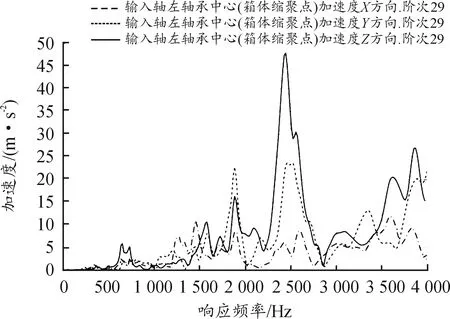
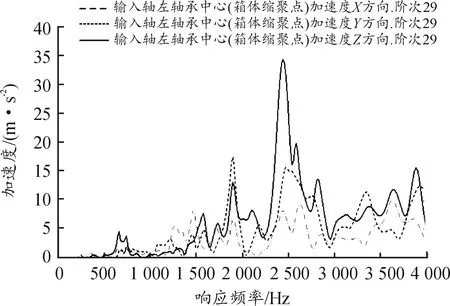
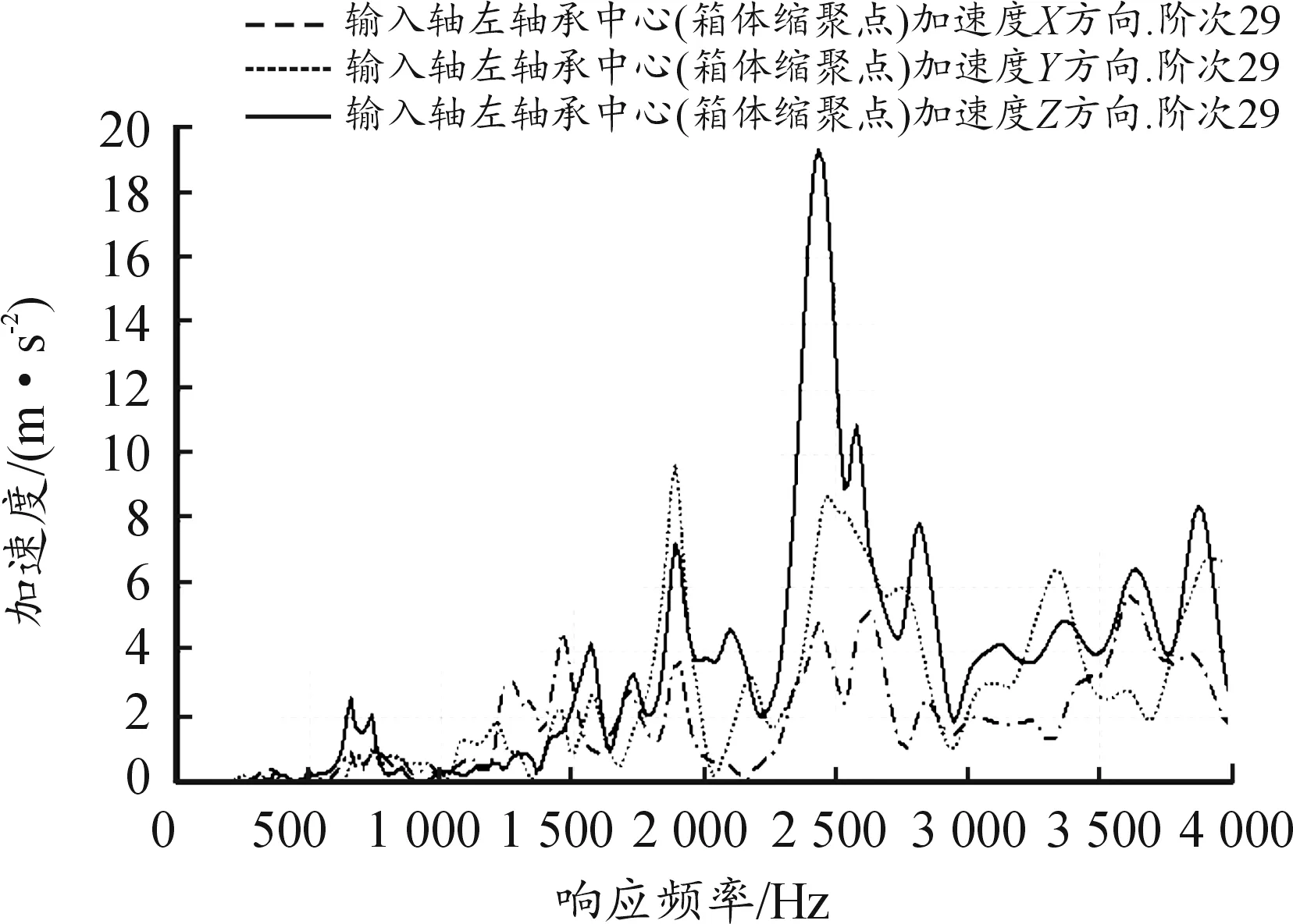
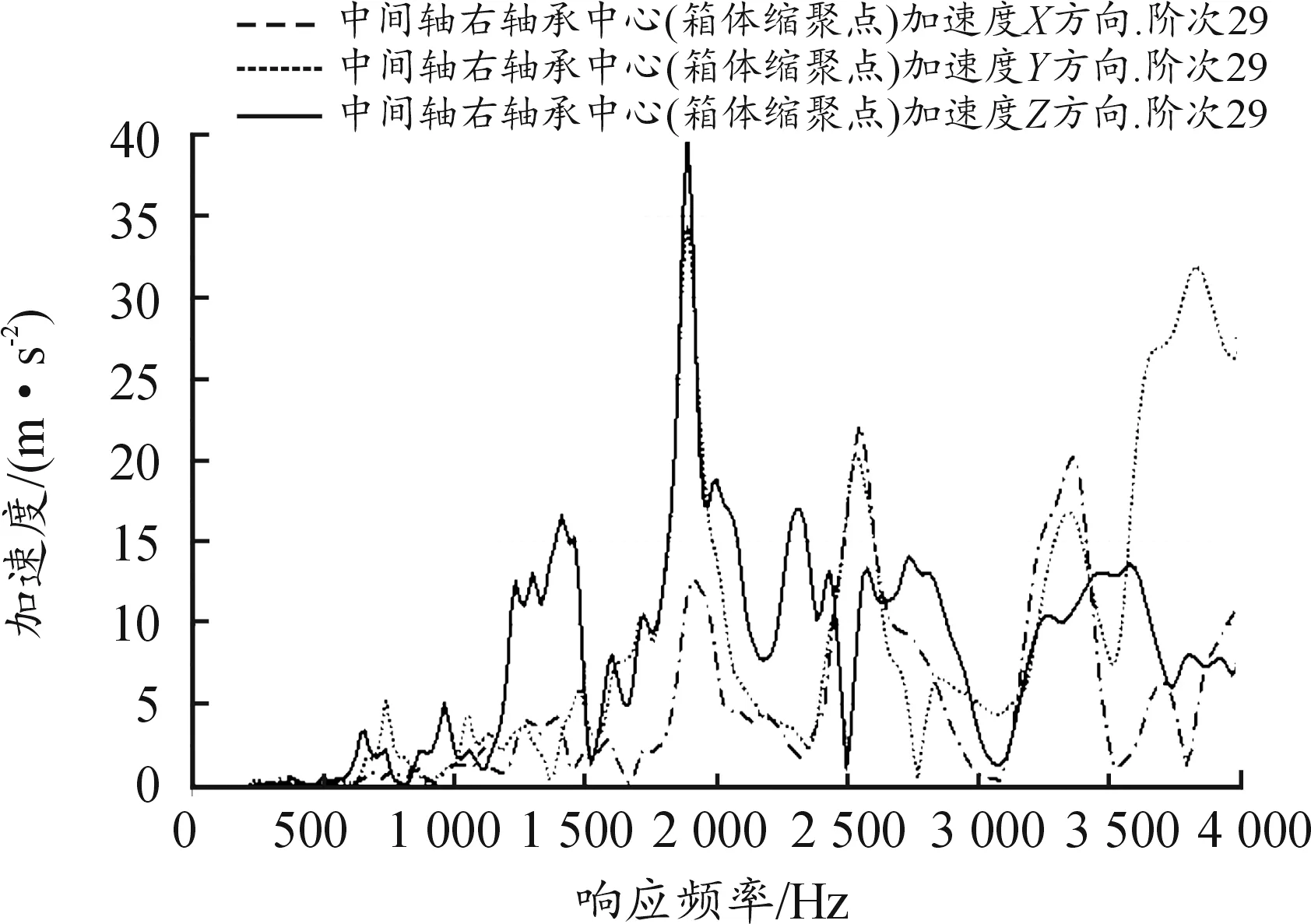
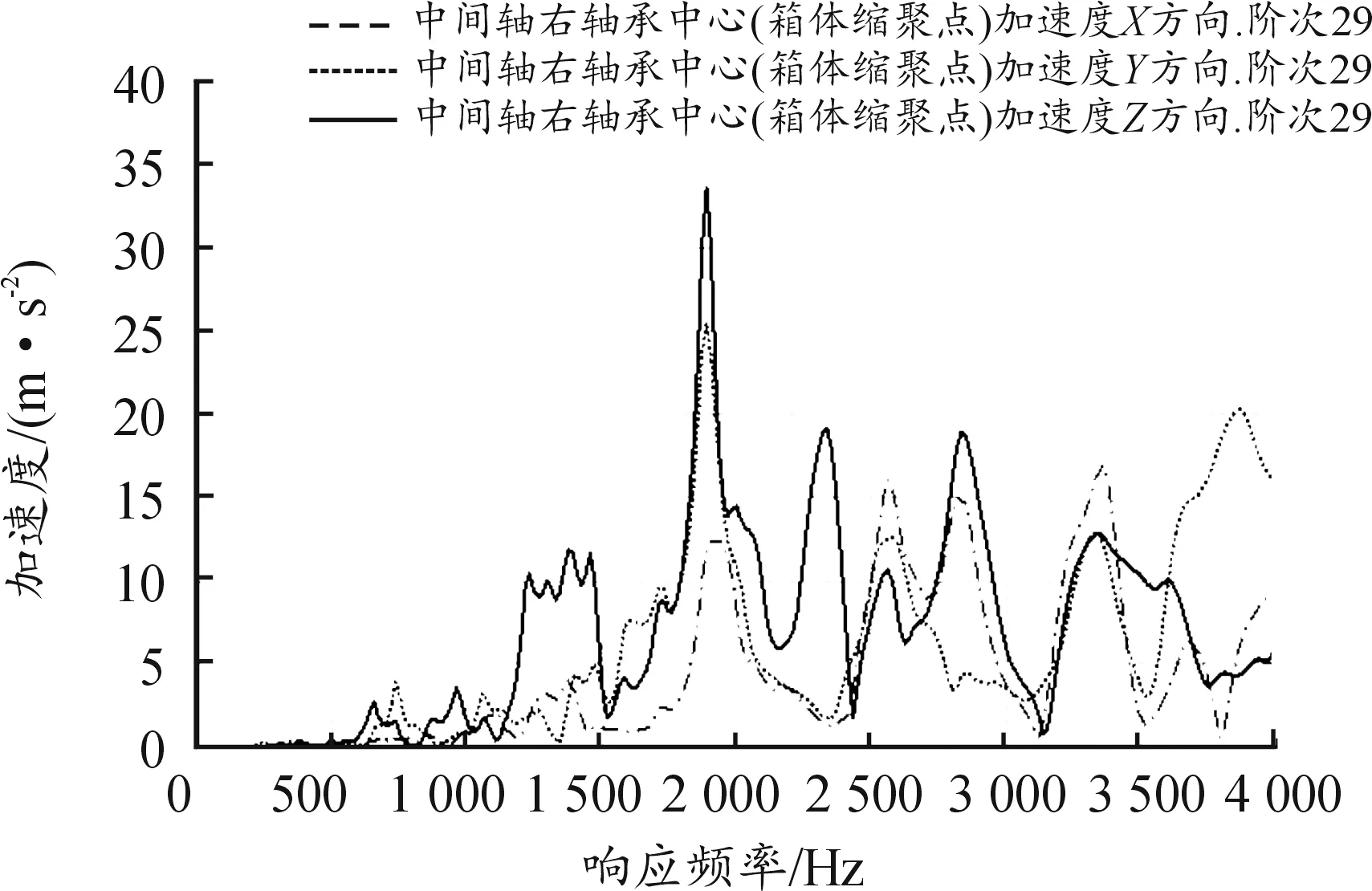
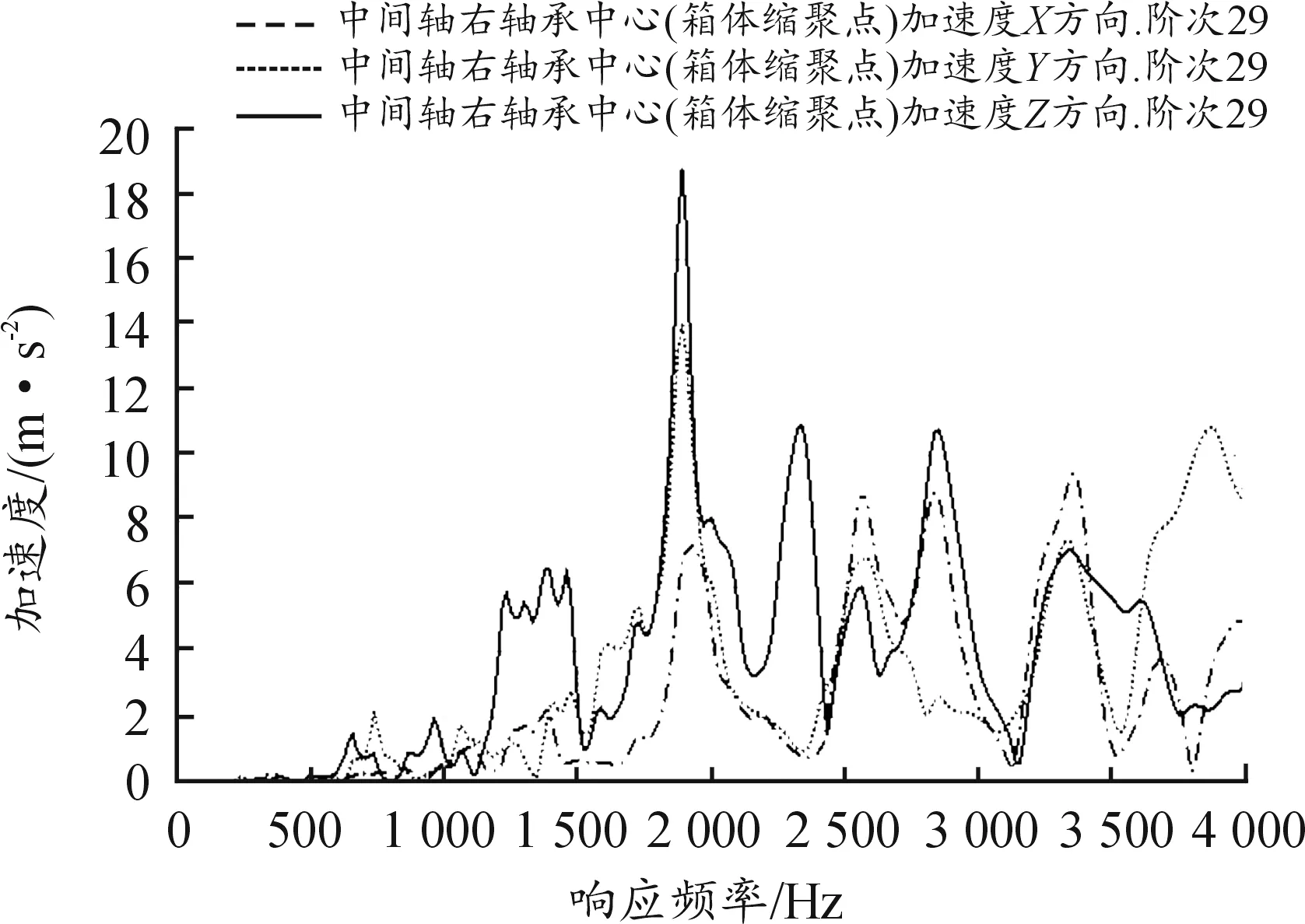
当bca1 (3) 当bca1≥B时: (4) 式中:C为啮合刚度;bca1为有效接触齿宽;Fm为圆周力;Fβy为啮合齿向误差。 齿向斜度的设计是为了补偿实际齿轮啮合过程中螺旋角的变化。齿向斜度的计算公式为: (5) 图3 齿向修形示意图 经验修形的数据根据微观修形ISO公式和工程经验,经过多次的反复仿真分析对比,得到3挡齿轮微观修形的数据如表2所示。 表2 3挡齿轮副经验修形参数 遗传算法是采用达尔文遗传学机理来求解非线性、多目标、多约束的复杂全局优化计算方法,是一种采用自适应全局优化概率搜索来模拟自然进化过程最优解的方法[15]。标准流程如图4所示。 图4 标准遗传算法流程框图 对于初始个体(祖先)采用函数生成随机数进行建立。根据工程经验确定3挡齿轮副的修形参数如表3所示。将其作为方案设计的约束条件。选择的初始种群规模(N)过少则会导致优化结果没有解的问题,初始种群规模过大,则计算的时间过长,影响效率,所以选择合适的种群规模将会决定遗传算法的实用性。此处取N=50。 表3 3挡齿轮修形参数范围 基于研究的目标之一是降低3挡40%工况下的传递误差的峰峰值,理论设计的齿轮传递误差是可以为零的,故所有工况的优化目标TE=0,(其中TE为传递误差)。在考虑降低传递误差的同时,能够降低齿面的单位长度载荷和最大接触应力,但若要降低齿轮的噪声,传递误差才是考虑的重点,因为单位长度载荷和最大接触应力是无法直接降低齿轮噪声,所以在设计传递误差时需要设定较大的权重,对于单位长度载荷和最大接触应力设置较小的权重。这样的设计目的是即使单位长度载荷和最大接触应力较大,但由于单位长度载荷和最大接触应力乘以权重系数,最后的得分也较小,所以设置不同的传递误差、单位长度载荷权重及最大接触应力系数对最终结果产生不同的影响。单位长度载荷和最大接触应力的经验设计原则是:对于目标的单位长度载荷和最大接触应力设定为对应未修形工况的一半,权重系数分别为目标单位长度载荷分之一和最大接触应力分之一,表4为设定目标的参数表。 遗传算法提供了3种遗传算子:选择算子、变异算子、交叉算子,3种算子各有所差异却又相辅相成,选择算子可以复制优秀“前辈”的基因;变异算子、交叉算子相对于选择算子能够扩大搜索空间,确保大概率找到最优方案。所以本文对于微观修形优化设计同时采用3种算子进行寻优。其中设定交叉算子Pc=0.2,变异算子Pm=0.3。 表4 设定目标参数 若遗传算法达到了预定设定的步长,且在搜寻的过程中找到了优秀的染色体,则结束整个搜寻过程,若未找到最优解则返回3.1节继续操作。 Romax V2遗传算法加入了更加复杂的变异算子。采用V1遗传算法的局限主要有2点:① 当其计算发生突变因素时,在某些区域存在无法搜寻的可能性,因此无法遍历所有可能的参数优化方案;② V1遗传算法以寻求最优解为优化目标,基本能够得到合适的目标函数,然而每次都不能保证原始数据的纯洁性,即容易偏离原始数据,引发发散,但Romax V2遗传算法在整个遗传的过程中可以保持原始数据的纯洁性,数据越大,越能得到最优解。因此,选择采用Romax V2遗传算法,设定20代遗传,设定求解方案时应满足3挡微观修形分析。图5为名义得分与候选点数显示结果,可以看出在1 000组候选方案中大多方案都集中在得分3~7分,且趋于收敛,说明该优化设置的参数合理。 图5 遗传算法寻优结果图 以40%工况为例来说明寻优得到的传递误差峰峰值与主动齿轮渐开线鼓形、渐开线斜度、齿顶修缘、齿向鼓形、齿向斜度5个参数的关系,如图6所示。要满足传递误差的减小,根据工程经验,传递误差在1 μm以下,综合3挡驱动工况,以传递误差、单位长度载荷、最大接触应力为优化目标,得出最优的修形优化参数如表5所示。 图6 主动齿修形参数与传递误差关系图 表5 遗传算法寻优结果 μm 分别将2组修形参数带入模型的微观修形模块,对修形前后的传递误差进行对比,结果如图7~9所示。由图可知,采用的2种修形方式均可降低传递误差峰峰值,未修形传递误差为0.98,采用经验修形得到传递误差为0.62,相较于未修行降低36.73%,采用基于遗传算法修形得到的传递误差为0.34,相较于未修形降低65.3%。 图7 修形前3挡齿轮传递误差曲线 图8 采用经验修形3挡齿轮传递误差曲线 图9 采用遗传算法3挡齿轮传递误差曲线 将2种修形得到的齿轮承载能力与修行前的齿轮承载能力进行对比分析,如图10~12所示。结果发现,2种修形方式都改善了齿面的接触情况。基于经验修形的单位长度载荷为236 N·m,相较于未修行降低34.99%;基于经验修形的最大接触应力为1 023 MPa,相较于未修形降低25.33%。基于遗传算法的单位长度载荷为221 N·m,相较于未修行降低39.39%;基于遗传算法的最大接触应力为967 MPa,相较于未修形降低29.42%。 图10 修形前3挡齿轮承载能力示意图 图11 基于经验修形后3挡齿轮的承载能力示意图 图12 基于遗传算法修形后3挡齿轮的承载能力示意图 在建立该变速器齿轮系统模型时,将输入轴的右端定义为坐标原点,所以输入轴右端为输入轴左轴承,具体模型标识如图13所示。齿轮动态的啮合力通过轴承传递到箱体,再间接的传到车身,从而产生噪声,所以本文通过对比修形前后轴承处的加速度大小来间接的反应变速器NVH性能。箱体完成缩聚后响应节点为轴承的中心位置,所以测试轴承中心位置的响应,完全可以反应箱体的表面振动响应。在3挡齿轮传递误差的一阶谐波和齿轮啮合刚度激励下对输入轴的左轴承和中间轴的右轴承进行修形前后的振动加速度进行对比,结果如图14~19所示。 图13 齿轮传动系统轴承位置示意图 图14 未修形输入轴左轴承处响应结果曲线 图15 经验修形输入轴左轴承处响应结果曲线 图16 遗传算法修形输入轴左轴承处响应结果曲线 图17 未修形中间轴右轴承处响应结果曲线 图18 经验修形中间轴右轴承处响应结果曲线 图19 遗传算法修形中间轴右轴承处响应结果曲线 采用2种方法修形后在传递误差激励下轴承中心位置的加速度相较于未修形的都明显降低,尤其是Z轴方向的加速度。其中输入轴左轴承在响应频率为2 448.4 Hz处,采用经验修形后响应节点处Z方向的振动加速度为34.55 m/s2,相较于未修形的Z向加速度47.86 m/s2降低了27.81%;采用基于遗传算法修形后响应节点处Z方向的振动加速度为19.32 m/s2,相较于未修形降低了59.63%。中间轴右轴承在响应频率为1 888.5 Hz处,响应节点的Y向和Z向均出现了峰值,采用经验修形后响应节点处Y和Z方向的振动加速度分别为25.52、33.61 m/s2,相较于未修形的Y、Z向加速度34.42、39.76 m/s2分别降低了25.86%、18.3%;采用基于遗传算法修形后响应节点处Y、Z方向的振动加速度分别为14.11、18.81 m/s2,相较于未修形分别降低了59.1%、52.7%。从上述结果的分析可知:采用合理的微观修形设计,尤其是齿形修形和齿向修形组合的修行方式可以改善变速器的NVH性能,说明齿轮的微观修形设计对于指导变速器的设计具有深远的意义,其中采用遗传算法得到的振动响应值较经验修形更优,也可以较好地预防变速器啸叫噪声的产生。 针对某款DCT变速器,采用Romax建立变速箱刚柔耦合模型,以3挡的齿轮为研究对象,对齿轮采用经验修形和基于遗传算法修形2种修形方式,结果表明:采用合理的修形均可以降低传递误差,提高齿轮的承载能力。基于遗传算法的齿轮修形相较于经验修形,虽最后计算得到的单位长度载荷和最大接触应力相差不大,但考虑到采用经验公式计算的微观修形参数的难点在于有部分参数难于求解,所以采用全局优化遗传算法具有明显的优势。最后通过测试轴承中心处(箱体缩聚响应节点)的动态响应,发现2种修形方法均可以改善齿轮系统的NVH性能,且采用遗传算法修形得到的振动响应结果更优。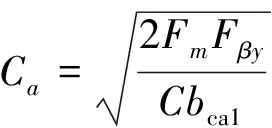
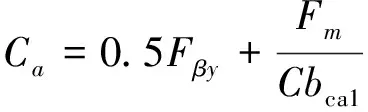
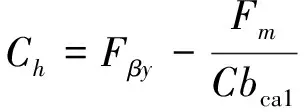
2.3 基于经验修形得到的微观修形数据
3 遗传算法简介
3.1 随机产生初始个体及初始种群规模确定

3.2 优化目标的确定
3.3 应用算子的选择

3.4 遗传算法的终止确定
3.5 基于遗传算法得到的修形数据
4 2种修形方法与修行前的对比分析
5 变速器NVH性能分析

6 结论

