一种研究死区非线性对系统频率特性影响的图解方法
刘 鹏,李怀兵,杨超凡,陈 婷,刘 凯
(北京精密机电控制设备研究所, 北京 100076)
死区非线性广泛存在于控制系统[1-3],在电动伺服系统中也经常用死区非线性来描述传动间隙。死区非线性会影响控制系统动态性能和稳态精度,并且会产生极限环振荡,影响系统稳定性[4-7]。目前已有较多文献研究死区非线性对系统稳定性的影响[8-11],但研究系统性能的影响因素的文献较少。综合运用描述函数法,等M圆、等N圆,以电动舵机为研究对象,通过一种图解方法分析了死区非线性对控制系统闭环频率特性的影响。
1 电动伺服系统
1.1 电动伺服系统传动机构
图1为典型的驱动飞行器舵片的电动舵机结构示意图。其运动传递过程为:电机转动通过齿轮副传递给滚珠丝杠副,丝杠螺母上安装有线位移传感器,将位置信号反馈给控制器,形成闭环控制。此外,丝杠螺母通过销轴与摇臂和连杆连接,通过舵轴最终驱动舵片偏转,丝杠螺母到舵片的传递过程没有进入闭环回路,属于开环控制,但是可以通过负载效应影响到闭环性能。
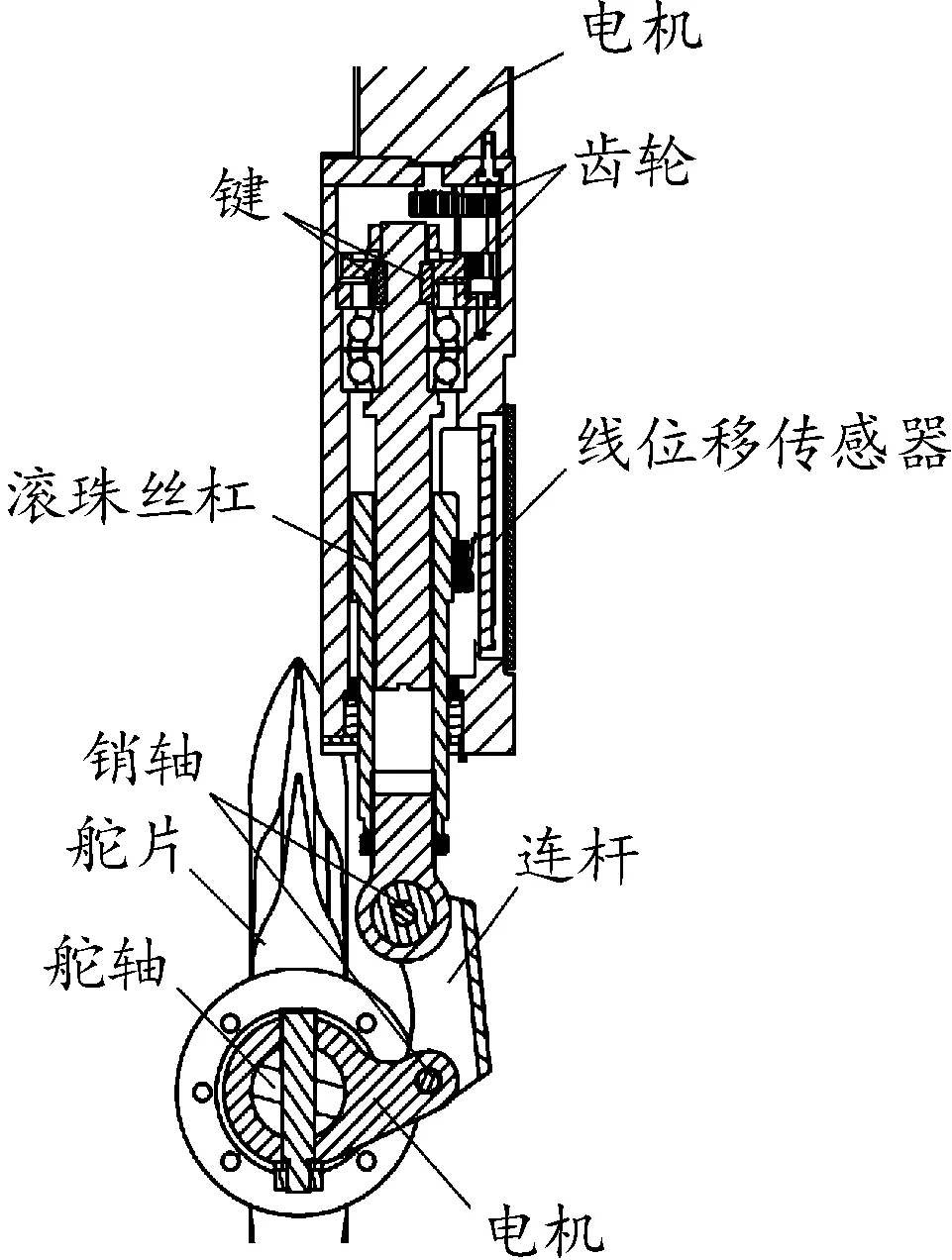
图1 电动舵机结构示意图
在闭环回路中,电机一般通过圆柱销或平键与主动齿轮连接,从动齿轮一般通过平键与滚珠丝杠连接,圆柱销一般为过盈配合,平键一般采用双键,可有效消除间隙。滚珠丝杠副一般通过增大钢球消除间隙。所以在闭环回路内部,传动间隙主要存在于齿轮副中。
在闭环回路外部,由于摇臂和连杆必须要相对转动,因此,销轴与销轴孔的配合需要有一定间隙,此传动间隙属于闭环外间隙,在本文中称为负载间隙。
1.2 电动伺服系统中传动间隙的数学模型
图2为用死区模型模拟间隙的齿轮传动数学模型,在该模型中,死区宽度代表齿轮间隙值,模型中各参数含义如下:K刚度为齿轮啮合刚度;i齿轮为齿轮减速比;JT为从动部分转动惯量;fT为从动部分粘性阻尼系数;KT为负载力矩系数。

图2 齿轮传动数学模型示意图
图3为用死区模型模拟间隙的连杆摇臂机构数学模型,在该模型中,输入为电动舵机中丝杠螺母的伸缩量,输出为舵片转动角度,死区宽度代表销轴与销孔的间隙值,模型中各参数含义如下:KW为负载等效刚度;L力臂为摇臂力臂长度;JW为负载转动惯量;fW为负载粘性力矩系数;K弧角为弧度角度转化系数;K角线=L力臂/K弧角,将舵片转角折合为丝杠螺母伸缩量系数;i为负载到电机的总减速比;KT为负载力矩系数。
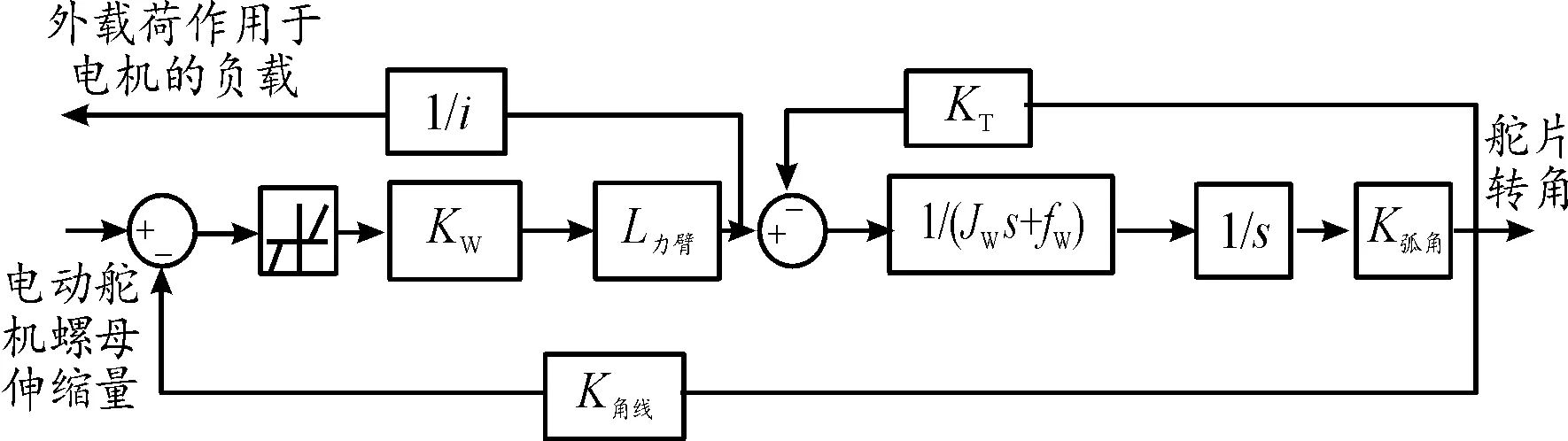
图3 连杆摇臂机构数学模型示意图
将上述模型放到系统中,可得到考虑间隙的电动舵机伺服系统数学模型。
2 负载间隙对伺服系统闭环频率特性的影响
只考虑负载间隙,不考虑闭环回路内的齿轮间隙,可得伺服系统模型,如图4所示。模型中参数定义如下:P为比例系数;U为供电电压;L为电机等效电感;R为电机等效电阻;Cm为电机力矩系数;Ce为反电动势系数;fd为电机粘性力矩系数;Jd为电机的转动惯量;i齿轮为齿轮的减速比;i丝杠为丝杠的减速比;K线角为作动杆伸出长度转化为舵轴转角的转化关系。
按图4模型进行仿真,以控制角度为输入,输入信号为r=1°sin(ωt),舵片转角为输出,负载间隙值分别取0、0.05、0.1 mm,求解不同频率响应的幅值和相位[12],系统的幅频特性及相频特性如图5所示。典型频率下的幅频数值见表1,相频数值见表2。

图4 考虑负载间隙的伺服系统模型示意图

表1 幅频特性

表2 相频特性
从仿真结果看,随着间隙的增大,在低频处,幅值会衰减,但随着频率的升高,幅值反而会增加;随着间隙的增大,相位变化不大。为何会出现这种情况,传动间隙是如何对系统频率特性造成影响的,可用图5中的图解方法进行探究。

图5 不同负载间隙下系统闭环bode图
按描述函数的理论[13-15],非线性环节可以看成一个变增益的环节,其增益值与输入幅值有关。按如下思路分析负载间隙对频率特性的影响:① 对系统等效变换以便于分析,为能通过开环频率特性得出闭环频率特性,需将研究对象转化为单位负反馈系统;② 计算系统在不同频率下非线性环节等效的增益值N(A);③ 将不同的N(A)代入单位负反馈系统的开环传递函数,得到含间隙的开环传递函数;④ 通过等M圆可以在单位负反馈系统开环幅相曲线上直观地读出间隙对系统闭环幅值特性的影响,通过等N圆可以直观地读出间隙对系统闭环相位特性的影响。
按上述理论进行分析,先对模型进行等效变换,将死区环节替换为一个变增益环节N(A),由于负载部分与舵机部分通过力的传递而产生耦合关系,通过移动比较点和引出点,将负载部分和舵机部分解除耦合关系,如图6所示。从图中可以看出,对于舵机部分而言,N(A)只会影响其内部回路的反馈系数,因此,认为N(A)对舵机部分频率特性影响较小。
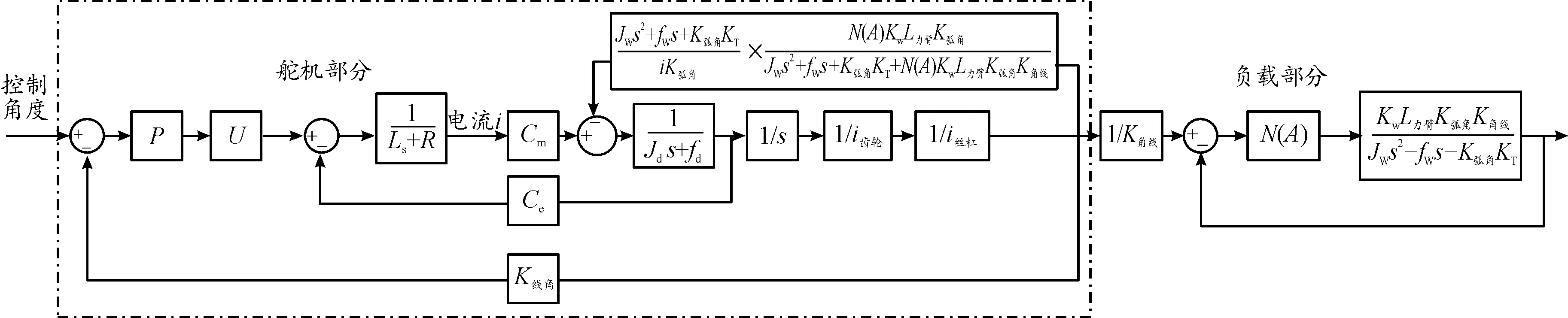
图6 模型等效变换结果
图6模型等效变换结果用图4所示模型进行仿真,以控制角度为输入,线位移传感器作为输出,分别计算不同间隙的线位移输出。从图7中可以看出,不同间隙值下,线位移幅频和相频曲线基本重合。因此,可以只研究负载部分。
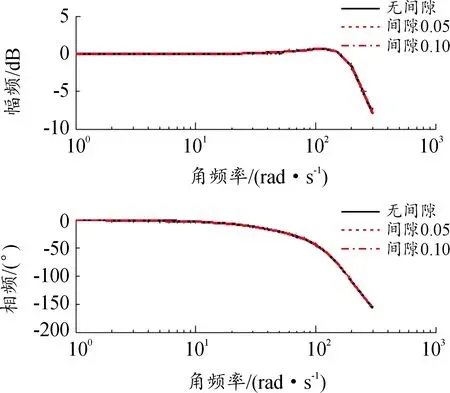
图7 不同负载间隙下系统线位移传感器输出bode曲线
为使用等M圆、等N圆进行研究,将负载部分等效变换为单位负反馈系统,如图6所示。由于单位负反馈回路与其他回路是串联关系,间隙环节只对单位负反馈回路有影响,所以,间隙对系统的影响可以简化为间隙对单位负反馈回路的影响。
2.1 单位负反馈回路开环幅相曲线
如图6所示,单位负反馈回路的开环传递函数为
(1)
死区环节的描述函数为:
A≥Δ
式中:A为输入信号幅值;2Δ为死区宽度。从公式中可以看出,N(A)不含虚部且值恒小于1。
计算死区环节的等效增益N(A)的取值有2种方法:① 计算处死区环节的输入值,然后代入描述函数公式得到N(A);② 分别对死区输出和输入信号进行数字傅立叶变换,幅值相除,即可得N(A)值。现采用第2种方法。表3为不同间隙、不同频率下,计算出的N(A)值。

表3 不同频率、不同间隙下的N(A)值
当N(A)=1时,得到无间隙时的开环幅相特性及开环幅相特性曲线。将不同间隙之下,不同频率处的N(A)值代入式(1),得到其开环幅相特性,画在复平面上就可以得到不同间隙下的开环幅相曲线,如图8所示。
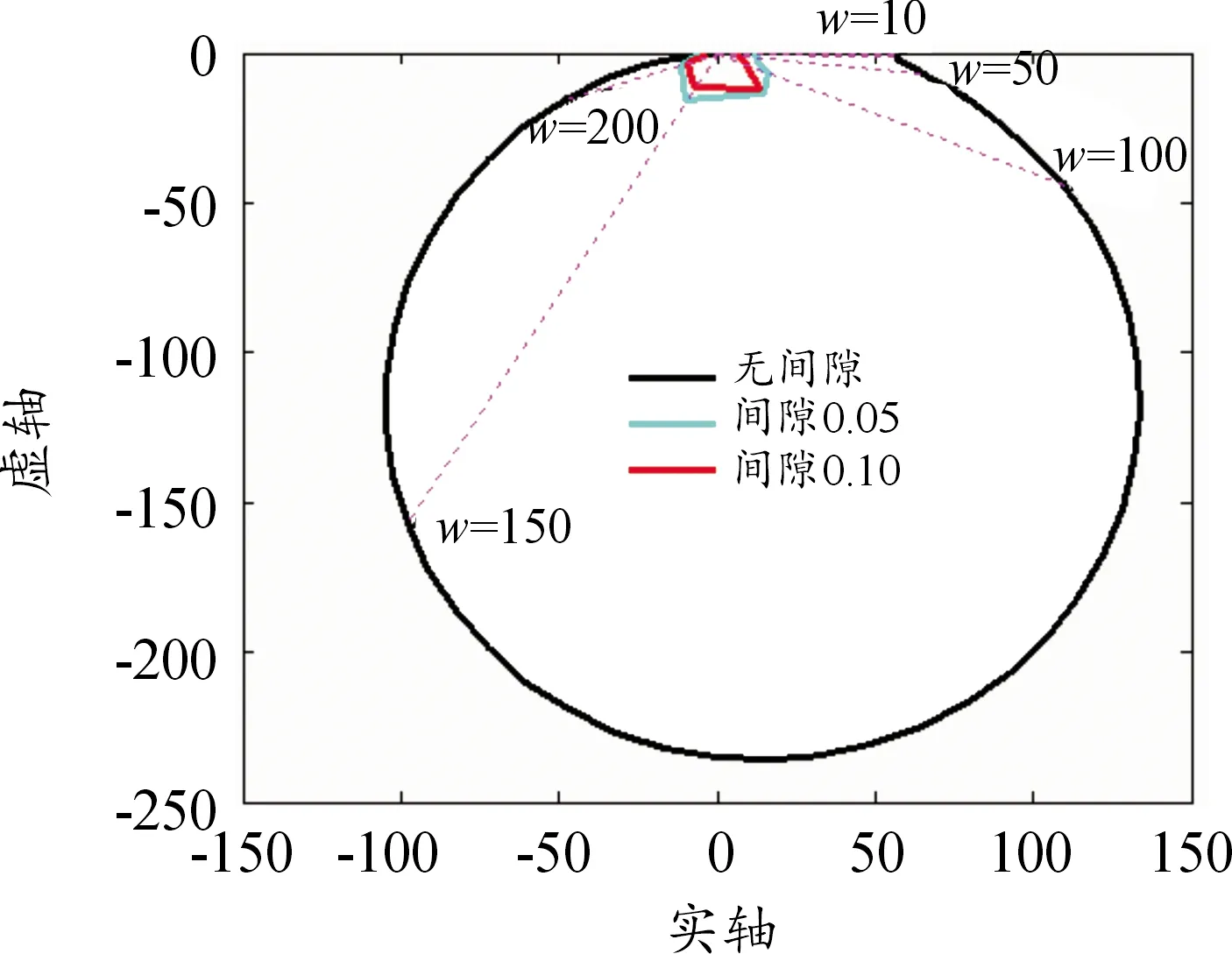
图8 不同间隙值下的开环幅相曲线
由于将N(A)视为一个小于1的纯比例环节,不影响相位,因此将各频率下幅相特性在复平面上的点与原点连接起来形成一条直线,当N(A)变化时,同一频率的幅相特性将在该直线上移动,死区环节的效果是使各频率对应的点在复平面上沿直线向原点移动。
2.2 系统闭环幅值特性
对于单位负反馈系统,通过等M圆可以直接在开环幅相曲线上读出闭环幅值特性。等M圆轨迹是一簇圆公式:
(2)
式中,M为系统闭环幅值特性。当M=1(0 dB)时,它是通过(-1/2,0j)点、平行于虚轴的一条直线。
当M>1(0 dB)时,随着M值的增大,等M圆半径越来越小,最后收敛于(-1,0j)点,且这些圆均在M=1(0 dB)直线的左侧;
当M<1(0 dB)时,随着M值的减小,等M圆的直径越来越小,最后收敛于原点,且这些圆均在M=1(0 dB)直线的右侧。
将等M圆画在上一节的开环幅相曲线中,如图9所示,从图中可以直接读出不同间隙下,单位负反馈环节各频点的闭环幅值。由于w=1~100 rad/s开环幅相曲线位于等M圆0 dB线右侧,因此随着N(A)值的变小,闭环幅值也变小;w=150~200 rad/s开环幅相曲线位于等M圆0 dB线左侧,随着N(A)值的变小,闭环幅值增大,这与图5及表1所示的仿真结果是一致的。

图9 等M圆与开环幅相曲线
由于系统闭环幅值还需叠加其他部分,通过前文分析,其他部分不受间隙影响,因此,从图中读出单位负反馈的闭环幅值的相对变化量与整个系统的闭环幅值的相对变化量是一致的。以w=50 rad/s的频点为例,如图10所示,直虚线为系统在w=50 rad/s频率下对应的直线,虚线圆即为等M圆,等M圆有无数个,每个等M圆对应一个闭环幅值。开环幅相曲线与频率直线的交点会位于某个等M圆上,从该等M圆可直接读出系统的闭环幅值。
在w=50 rad/s处,无间隙时,开环幅相曲线与-0.130 dB的等M圆相交,间隙为0.05 mm时,与-0.657 dB的等M圆相交,间隙为0.1 mm时,与-1.155 dB的等M圆相交。在不同间隙下,图解法与仿真结果比较如表4所示。
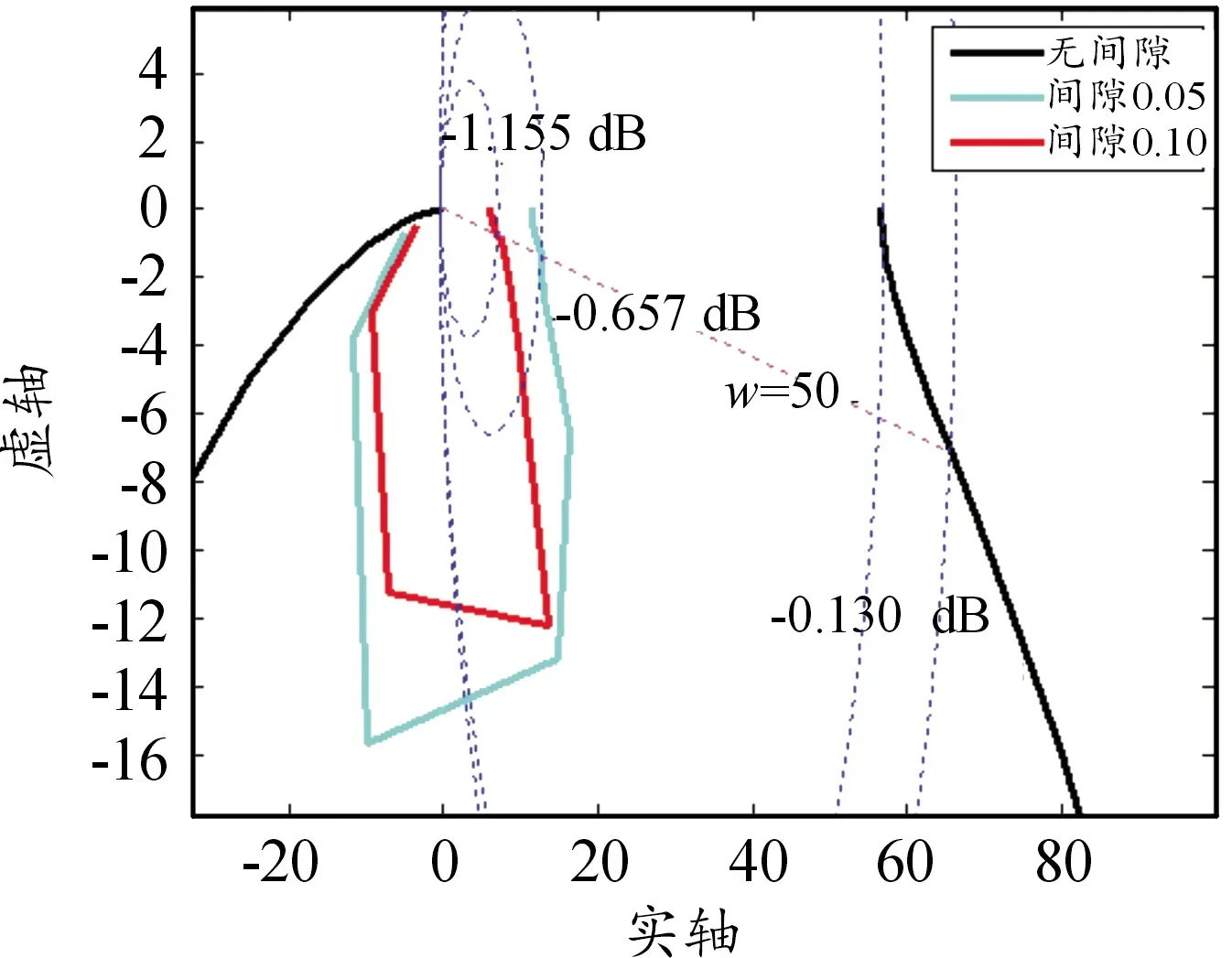
图10 等M圆与开环幅相曲线相交情况

表4 w=50 rad/s幅值相对变化量比较
从表4可以看出,图解法与仿真结果趋势一致,具体数值稍有差异。这是由于描述函数是一种近似方法,忽略了高次谐波的影响,在实际系统中,死区环节的输入并非理想的正弦函数。若只需快速估计出死区非线性对系统影响,图解法的精度是足够的。
在等M圆上读数时有以下特点:
1)N(A)为纯比例时,不同间隙,同样频率时,系统幅相特性在复平面上都在一条直线上。当该直线穿过较多的圆,即等M圆越密集时,幅值变化较为剧烈,由于等M圆在无穷远处比较稀疏,在圆心处及靠近0 dB线处比较密集,因此当直线靠近圆心和0 dB线时,幅值变化较大,即开环幅值大时,闭环幅值变化小,开环幅值小时,闭环幅值变化大。
2) 当频率对应的直线趋近于等M圆的法线时,幅值变化较大。
3) 当频率对应的直线趋近于等M圆的切线时,幅值变化较小。
上述特点对用等N圆读取闭环相位时同样适用。
2.3 系统闭环相位特性
对于单位负反馈系统,通过等N圆可以直接在开环幅相曲线上读出闭环相位特性。
等N圆也为一簇圆。其方程为
(3)
式中,N=tanφ,φ为闭环频率特性的相角。
将等N圆叠加到开环幅相曲线上,可以直接读出闭环相位,如图11所示。由于频率对应的直线趋于等N圆的切线方向,因此闭环相位特性变化不大,从图5和表3的仿真结果也可以印证。
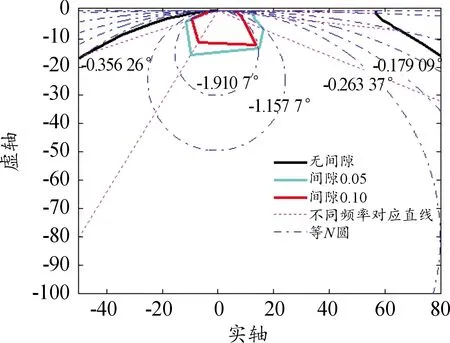
图11 等N圆与开环幅相曲线
3 闭环内间隙对伺服系统闭环频率特性的影响
作为图解法的应用,分析闭环内齿轮传动间隙对伺服系统闭环频率特性的影响。图12为考虑内部间隙的伺服系统模型,化简为单位负反馈系统,如图13所示。
取N(A)=1时,得到无间隙时开环幅相特性曲线,同时可得到每个频率对应的直线,如图14。与图7相比,每个频率的开环幅值均大10倍以上,根据前文总结的图解法读图特点,可知当闭环内间隙变化时,系统闭环频率特性变化不会很大。用图12所示模型进行仿真,仿真结果如图15所示,不同间隙下系统闭环幅值和相位特性基本重合。

图12 考虑内部间隙的伺服系统模型示意图

图13 伺服系统模型等效化简结果
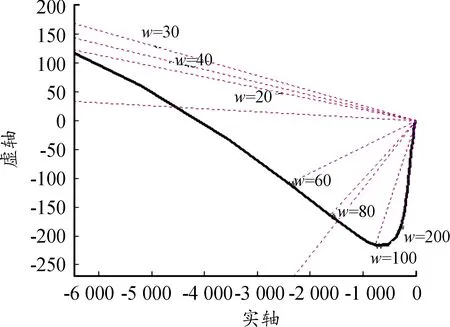
图14 系统开环幅相曲线

图15 系统仿真结果曲线
4 试验验证
为了验证仿真及分析结果,进行了电动伺服系统频率测试试验。加工尺寸不同的销轴,使配合间隙分别为0.05、0.1 mm,将伺服机构安装在负载台上,试验结果如图16所示,其幅值和相位变化趋势与图5的仿真结果一致。由于仿真模型中只考虑了负载间隙带来的死区非线性而未考虑其他非线性环节,因而仿真结果与试验结果存在一定差异。

图16 试验结果曲线
5 结论
1) 通过等效变换将系统变换为单位负反馈系统,通过等M圆、等N圆及线性部分的开环幅相曲线直观地观测到间隙对系统频率特性的影响。
2) 死区非线性对系统闭环频率特性的影响取决于不考虑死区环节时的线性部分,将各频率下幅相特性在复平面上的点与原点连接起来形成一条直线,死区环节的效果是使各频率对应的点在复平面上沿直线向原点移动。
3) 从图解法及仿真结果都可得出负载间隙比闭环内的间隙对系统闭环频率的影响更大。

