时变流体中悬臂梁的振动特性分析

邵明玉，李 涛，马驰骋，张忠伟，邵素娟

(山东理工大学 交通与车辆工程学院， 山东 淄博 255000)

流固耦合系统广泛存在于海洋石油管道、水下设备、船舶、潜艇和潜射弹道导弹等应用中，周围的流体会对结构的频率和阻尼产生不同程度的影响。在某些情况下，结构会在流动或变深度的流体中振动，流体的流动速度及浸没深度会对结构的振动产生额外的附加效应。为了对结构的振动进行抑制或主动控制，保证结构安全工作，必须对结构在时变流体中的振动特性进行详细分析。

在流固耦合特性研究中，大都忽略流体黏性和时变特性的影响，将流体对结构的作用简化为附加质量[1]，以分析其对结构频率的影响，而流体本身的运动则基于速度势理论求解[2-3]。对于尺寸较大的结构，雷诺数较大，不计黏性引起的误差很小，可以忽略。而对于微尺度结构，雷诺数较小，黏性对结构的频率和阻尼均会产生较大的影响。针对悬臂梁在黏性流体中的振动问题，Blom等[4-5]将梁简化为串珠模型，求解了作用在梁上的流体力，分析了梁在黏性流体中的频率和阻尼。Kirstein等[6]基于N-S方程求解了无限长圆柱体在流体中振动时的流体动力学函数，并分析了悬臂梁在黏性流体中的振动问题。Sader等[7-10]对圆柱梁的流体动力学函数进行了修正，导出了矩形截面梁的流体动力学函数，并研究了矩形截面悬臂梁在不同流体环境中的振动特性。随着计算流体动力学的发展，Liu等[11-13]对梁在流体中的振动稳态进行了数值分析，并通过双向流固耦合方法研究了梁和运动流体间的相互作用[14]。

目前，悬臂梁流固耦合振动研究大都针对流体所引起的附加质量，以及微尺度机械中黏性的效应，而针对悬臂梁在流动或变深度液体中的流固耦合问题则研究较少。

本文基于N-S方程的近似解，导出了悬臂梁在时变流体中的运动方程，分析了流体浸没深度、流动速度、黏性及梁几何尺寸对流固耦合系统频率和阻尼的影响，并通过纽马克-β法求解了悬臂梁在下降流体中的瞬态响应。

1 数学模型

1.1 几何模型

悬臂梁在时变流体中振动的流固耦合系统如图1所示。悬臂梁的下端固定，上端自由，梁的总长度L=180 mm，厚度δ=1 mm，宽度b=10 mm，材料为铝。流体从容器底部流入或流出，速度为v(t)，沿着梁长度方向(x方向)为正，流体浸没梁的深度为h(t)。流体的种类为水或重油。

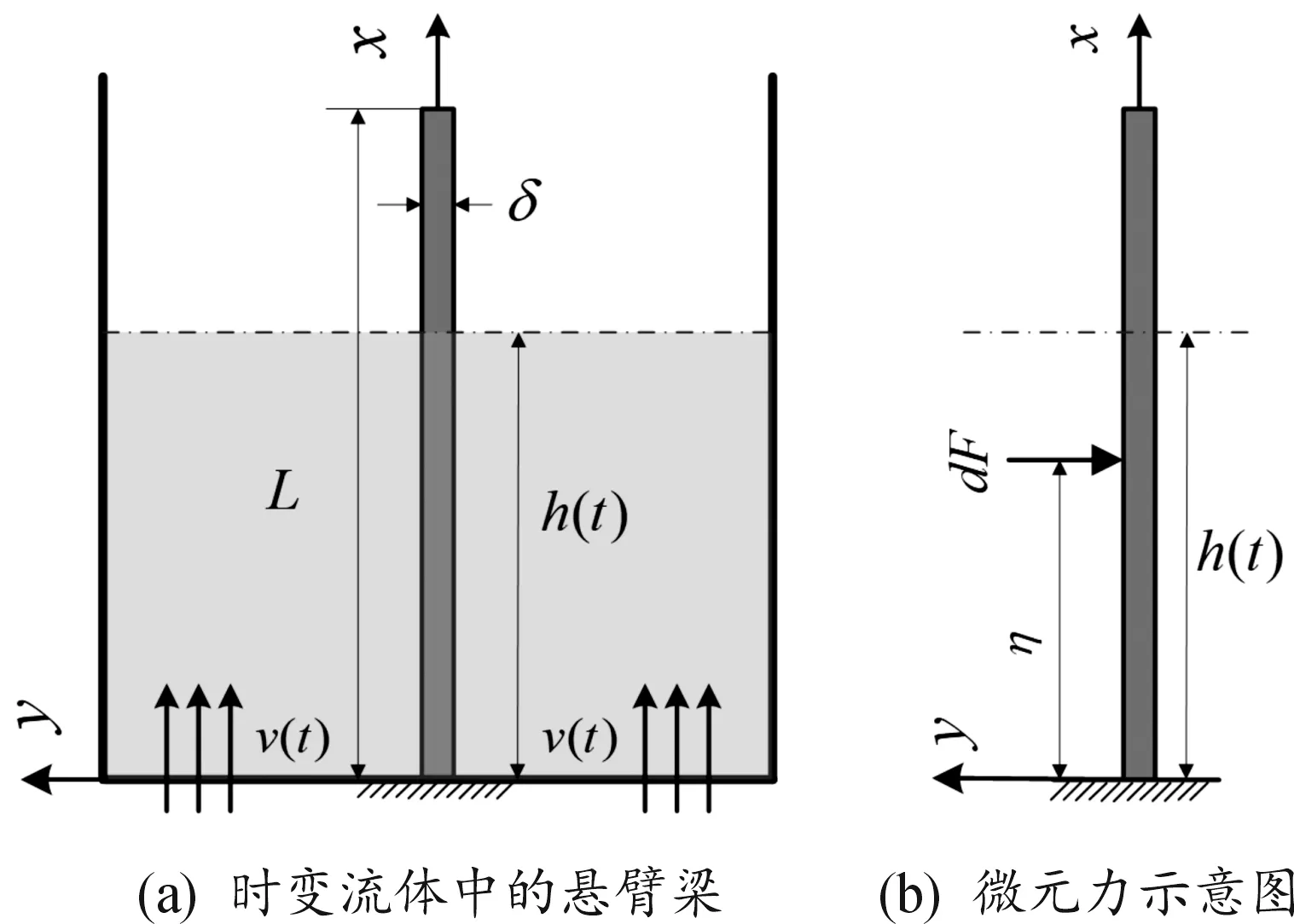
图1 流图耦合系统示意图

1.2 流动动力学函数

悬臂梁在流体中做横向振动时，梁上作用的流体力可通过周围流体的N-S方程而求得。忽略质量力，不可压流体的N-S方程和连续方程可以表示为：

(1)

▽·u=0

(2)

式中：ρf为流体密度；u为流体速度矢量；p表示压强；μ表示动力黏度，假设为常数。矩形梁做简谐振动时，上述方程的理论解难以求得，可通过对圆柱梁的解修正得到。假设直径为b的无限长圆柱在流体中以频率ω做简谐振动，其位移为：

u(t)=u0eiωt

(3)

单位长度圆柱体上的流体力可表示为[15]：

(4)

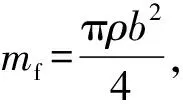
F(t)=mfω2Re(H)u0eiωt+imfω2Im(H)u0eiωt

(5)

将上式写为圆柱的速度和加速度的函数，即：

(6)

式中：βa=mfRe(H)，表示流体引起的附加质量；βv=-ωmfIm(H)，表示流体阻尼。

流体动力学函数H的完整表达式是一个复杂的贝塞尔类函数[6]，对于无限大的黏性流体区域，H可表示为：

(7)

式中：α=iRe，Re=ρfωb2/4μ表示雷诺数；K0和K1分别是零阶和一阶的第二类修订贝塞尔函数。对于雷诺数足够大的无限黏性流体区域，流体动力学函数H可以简化为：

(8)

图2(a)中给出了不同雷诺数下流体动力学函数的精确解和近似解。从图中可以看出，当雷诺数Re>102时，近似解和精确解吻合良好。

矩形梁在流体中做简谐振动时，周围流体的运动与圆柱体对应的流场类似，其流体动力学函数可通过圆柱体的流体动力学函数修正而得到[6]，即：

H′(ω)=F(ω)H(ω)

(9)

式中：F(ω)是与频率有关的修正函数[6]。

图2(b)中给出了圆柱体和矩形梁在流体中简谐振动时流体动力学函数的对比曲线，可以看出，当Re>102时，两者相差很小。

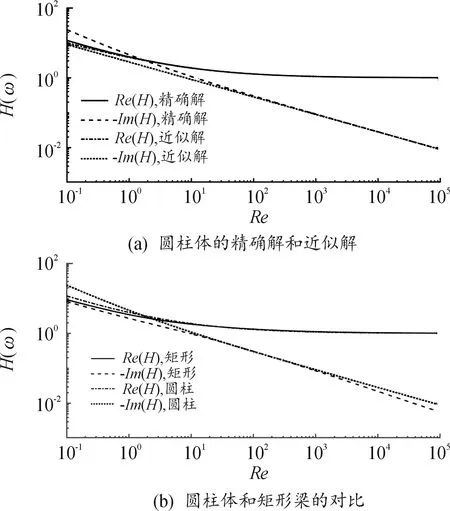
图2 不同雷诺数的流体动力学函数曲线

1.3 悬臂梁运动方程

假设梁在时变流体中横向简谐振动时，流体沿着梁长度方向的流动与流体随梁的横向振动互不干涉，即忽略长度方向的切应力，仅考虑梁横向振动的流体阻力，单位长度梁上的分布载荷可表示为：

(10)

在图1(b)中，坐标η表示流体沿着梁长度方向的坐标，取长度为dη的微元，并将微元上的载荷视为作用在η处的可移动集中载荷，则有：

(11)

根据欧拉-伯努利梁理论和牛顿运动定律，可得在微元集中载荷作用下悬臂梁的运动方程为[16]：

(12)

式中：EI为梁的抗弯刚度；ρb为梁的密度；A为梁的横截面积；δ(x)为Dirac函数。

采用模态叠加法对梁的运动进行坐标变化：

w(x,t)=∑jφj(x)qj(t)

(13)

式中：φj(x)表示第j阶模态振型；qj(x)表示第j阶振型对应的广义坐标。

研究表明，采用梁在真空中的振型可获得足够的精度[2]，即：

(14)

将式(13)代入梁的运动方程(12)可得：

(15)

求导后可得：

(16)

式中：v表示流体沿着梁长度方向的流动速度；a表示加速度。

将上式两端同乘以φi(x)，并在(0，L)范围内积分，可得：

(17)

假设运动流体微元对梁横向振动的影响可以线性叠加，流体浸没梁的高度为h(t)，忽略空气对梁的作用力，将上式在(0，h)范围内积分可得：

(18)

上式中，各矩阵元素的表达式为：

(19)

悬臂梁在时变流体中的运动方程可写为：

(20)

式中：M0表示梁的广义质量矩阵；K0表示梁的广义刚度矩阵；Ma,Ca,Kaa,Kav表示由梁的加速度引起的附加广义质量矩阵、广义阻尼矩阵和广义刚度矩阵；Cv,Kv表示由梁的速度所引起的附加广义阻尼矩阵和广义刚度矩阵。

从上式中可以看出，悬臂梁在时变流体中振动时，除流体本身的固有阻尼外，还有与流体运动相关的附加阻尼和附加刚度。值得注意的是，附加阻尼与流体速度成正比，当流体沿着梁长度方向下降时，将会引起负的附加阻尼，产生不利影响。

2 频率特性分析

2.1 方法验证

悬臂梁在流体中振动的固有频率可通过求解下述特征方程的根而得到：

(21)

式中：ωf表示流体中梁的无阻尼自振频率。

流体流动速度不大，或者梁的厚度较大时，流体所引起的附加广义刚度远小于梁自身的广义刚度，梁在流体和真空中的固有频率之间的关系可表示为：

(22)

式中：κn为无量纲附加质量因子。对于悬臂梁的一阶振动，单位长度上的无量纲质量因子可表示为：

(23)

(24)

可见，对于真空中固有频率一定的梁，其附加质量因子与流体的密度、黏性以及梁的宽度有关。文献[3]中采用速度势理论求解了梁简谐振动时周围无黏流体的运动，以及梁上作用的流体载荷，根据其方法得到的梁一阶振动附加质量因子为：

(25)

式中：a1,a2表示梁到容器两侧的距离。

根据文献[1]得到的梁一阶振动时单位长度上的附加质量因子为：

(26)

对比式(24)可以发现，文献[1]的方法没有考虑黏性的影响。采用本文方法及文献方法得到的悬臂梁完全浸没在流体(水和重油)中的一阶固有频率见表1。结果表明，对于水和高温时的重油，黏性的影响可以忽略，2种方法得到的结果吻合较好。而对于低温时的重油，黏性引起的附加质量较大，不考虑黏性会引起较大的误差。

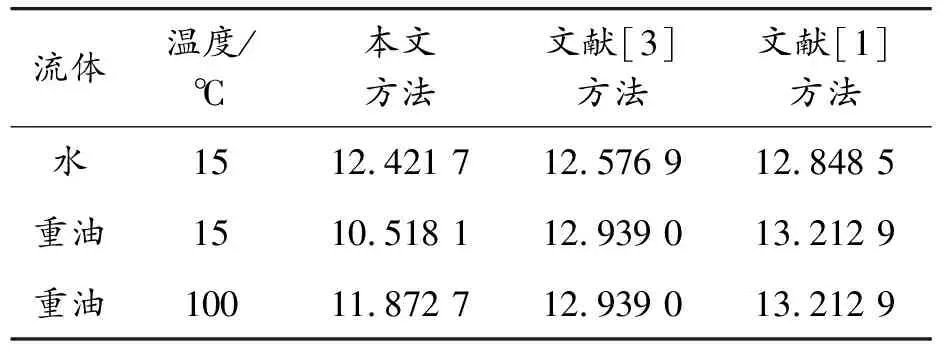
表1 不同方法得到的悬臂梁一阶固有频率

2.2 参数分析

式(19)(21)(24)表明，对于真空中固有频率一定的悬臂梁，其在流体中的固有频率与流体的浸没深度、黏性、流速及梁的宽度有关。

梁在水和重油中的一阶固有频率随浸没深度的变化如图3所示。可以看出，当流体的浸没深度较小时，梁的一阶固有频率基本不受影响，而当流体的浸没深度超过梁长度的一半时，梁的一阶固有频率随浸没深度的增加而迅速降低，即对于梁的一阶振动，其固有频率主要受到自由端流体的影响。

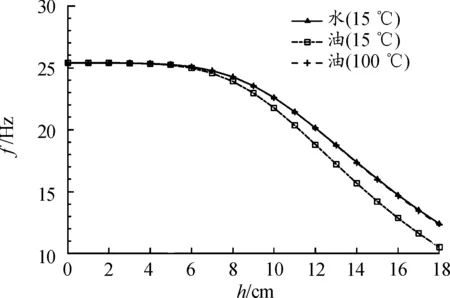
图3 不同浸没深度的一阶固有频率变化曲线

雷诺数较小时，流体引起的附加质量会受到黏性的影响，而对于有些流体，黏性会随温度的升高而迅速下降，如重油。高温时梁的弹性模量也会随温度升高而减小，但在本文研究的温度范围内几乎不变，其影响可以忽略；此外，由于梁和流体具有相同的温度，温度应力的影响也忽略不计。

图4给出了水和重油的黏性，以及完全浸没的悬臂梁的一阶固有频率随温度的变化曲线。从图中可以看出，水的动力黏度较小且随温度变化不大，梁的固有频率基本不变，接近无黏解。而重油低温时重力黏度较大，黏性使得附加质量较大，频率较低；随着温度升高，动力黏性迅速下降，频率逐渐增大，并趋向无黏解。

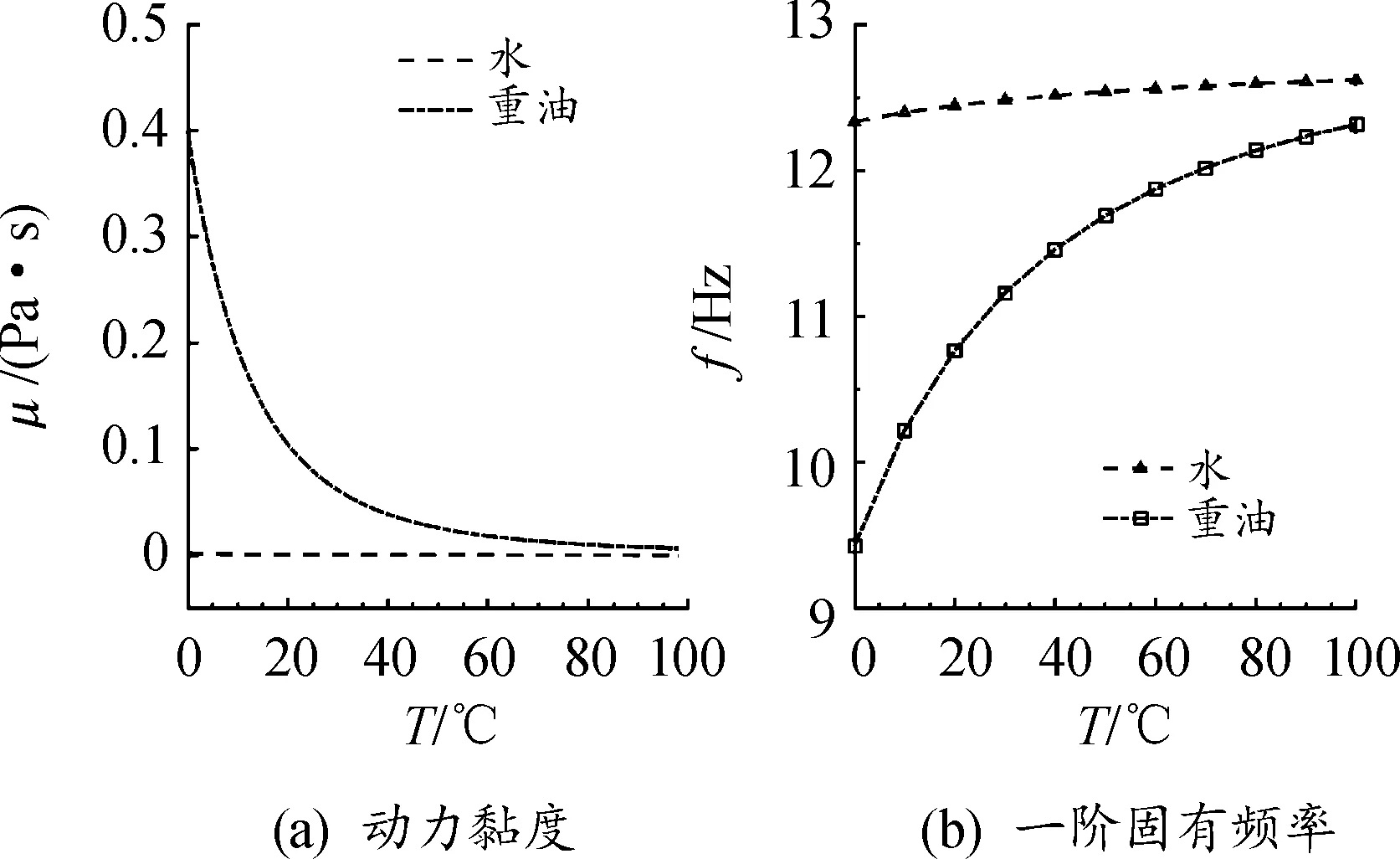
图4 不同温度的动力黏度和一阶固有频率变化曲线

当梁自身的刚度较小或流体的流动速度较大时，流体流动所引起的附加刚度对频率的影响不可忽略。不同流体中，完全浸没的梁的一阶固有频率随流动速度的变化规律如图5所示。可以发现，对于水和重油，梁的固有频率均随流动速度的增加而增大。从式(19)中可以发现，对于确定的梁，附加刚度还与流体的密度和黏性有关。对比15、100 ℃重油中的频率，低温时，重油的雷诺数较小，黏性影响更大，固有频率随速度的变化更加明显。

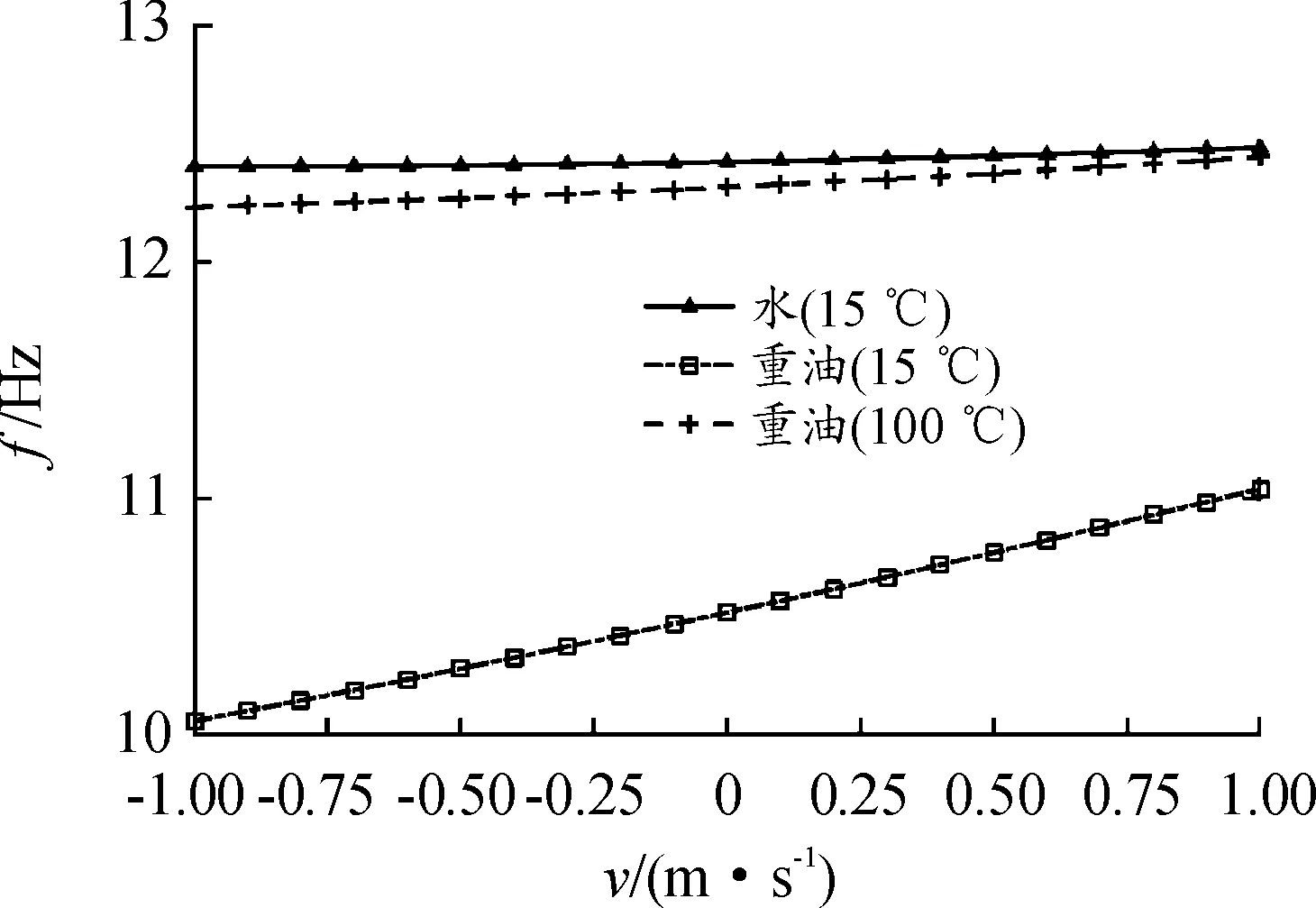
图5 不同流动速度的一阶固有频率变化曲线

除流体参数外，梁的宽度也会对其在流体中的固有频率产生重要影响。图6中给出了悬臂梁在不同流体中的一阶固有频率随梁宽度的变化。结合式(24)可以看出，梁的宽度增加时，流体引起的附加质量逐渐增大，梁的一阶固有频率逐渐减小。

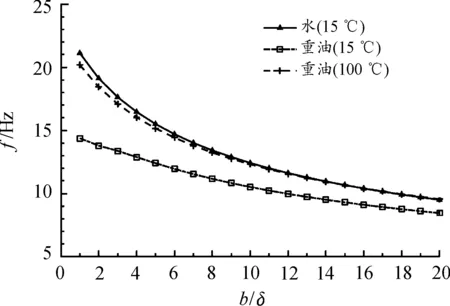
图6 不同宽度的一阶固有频率变化曲线

3 阻尼特性分析

忽略悬臂梁本身的结构阻尼，梁在时变流体中一阶振动的阻尼比可以表示为：

(27)

上式表明，系统的阻尼由2部分组成：一是流体黏性产生的固有阻尼，二是流体沿着长度方向移动引起的附加阻尼。可以看出，系统阻尼比同样受到流体运动参数和梁尺寸参数的影响。

完全浸没的悬臂梁一阶振动的阻尼比随流体流动速度的变化如图7所示。

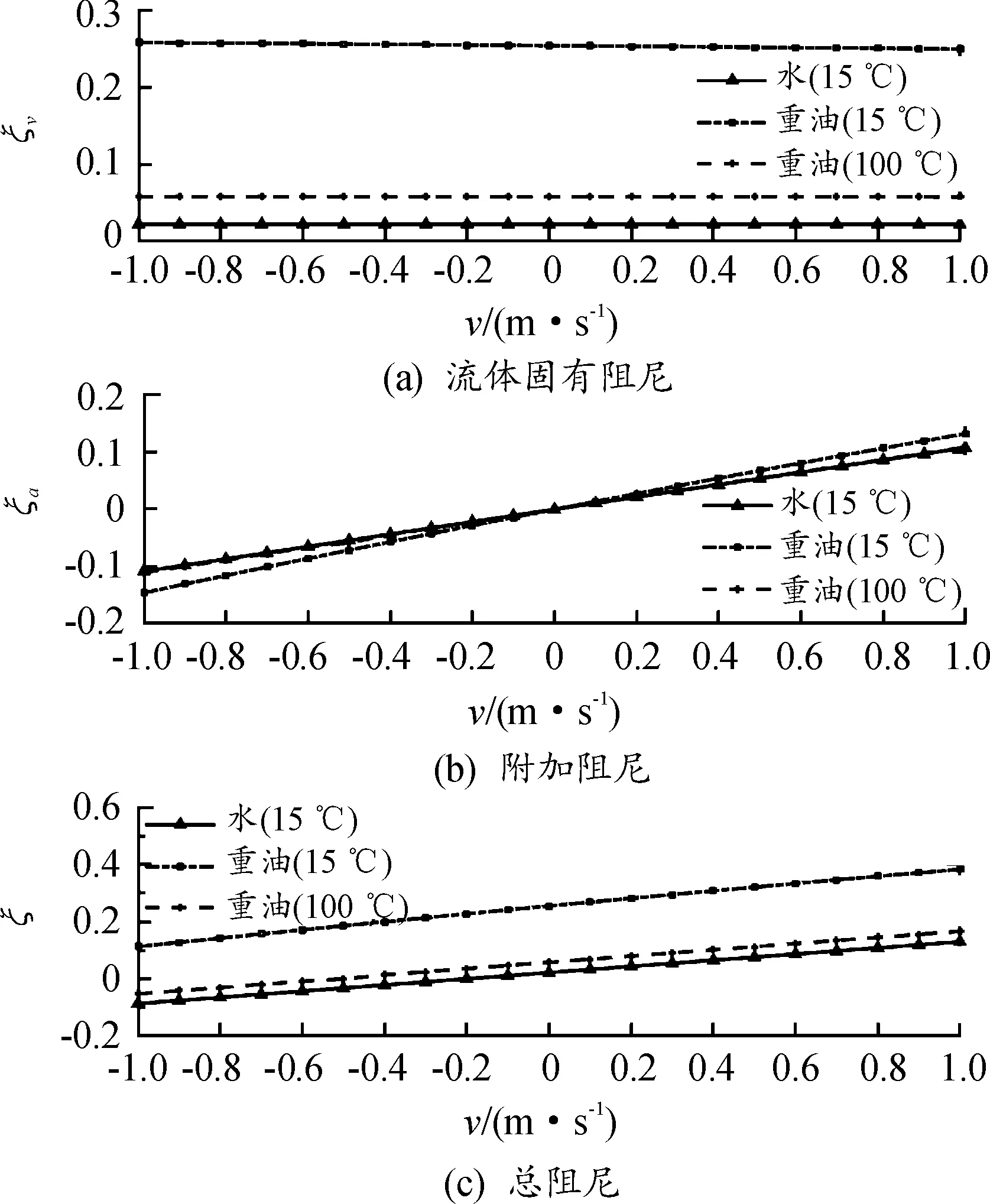
图7 不同流动速度的阻尼比曲线

由图7可以看出，流体的固有阻尼不随速度发生变化，而附加阻尼随流动速度的增加而迅速增大，总阻尼也随流动速度的增加而增大。对于黏性较小的情况，随着速度逐渐增大，附加阻尼成为系统阻尼的主导因素。

此外，还可以发现，当流体沿着梁长度方向下降时，将会引起负的附加阻尼，会对系统产生不利影响，甚至引发结构破坏。

完全浸没悬臂梁的一阶振动阻尼比随温度的变化如图8所示。当温度升高时，重油的动力黏性迅速减小，导致固有阻尼下降。重油中的附加阻尼也随温度升高而逐渐下降，但变化不大，系统总阻尼减小。而水的动力黏性随温度变化不大，系统阻尼基本不受温度的影响。

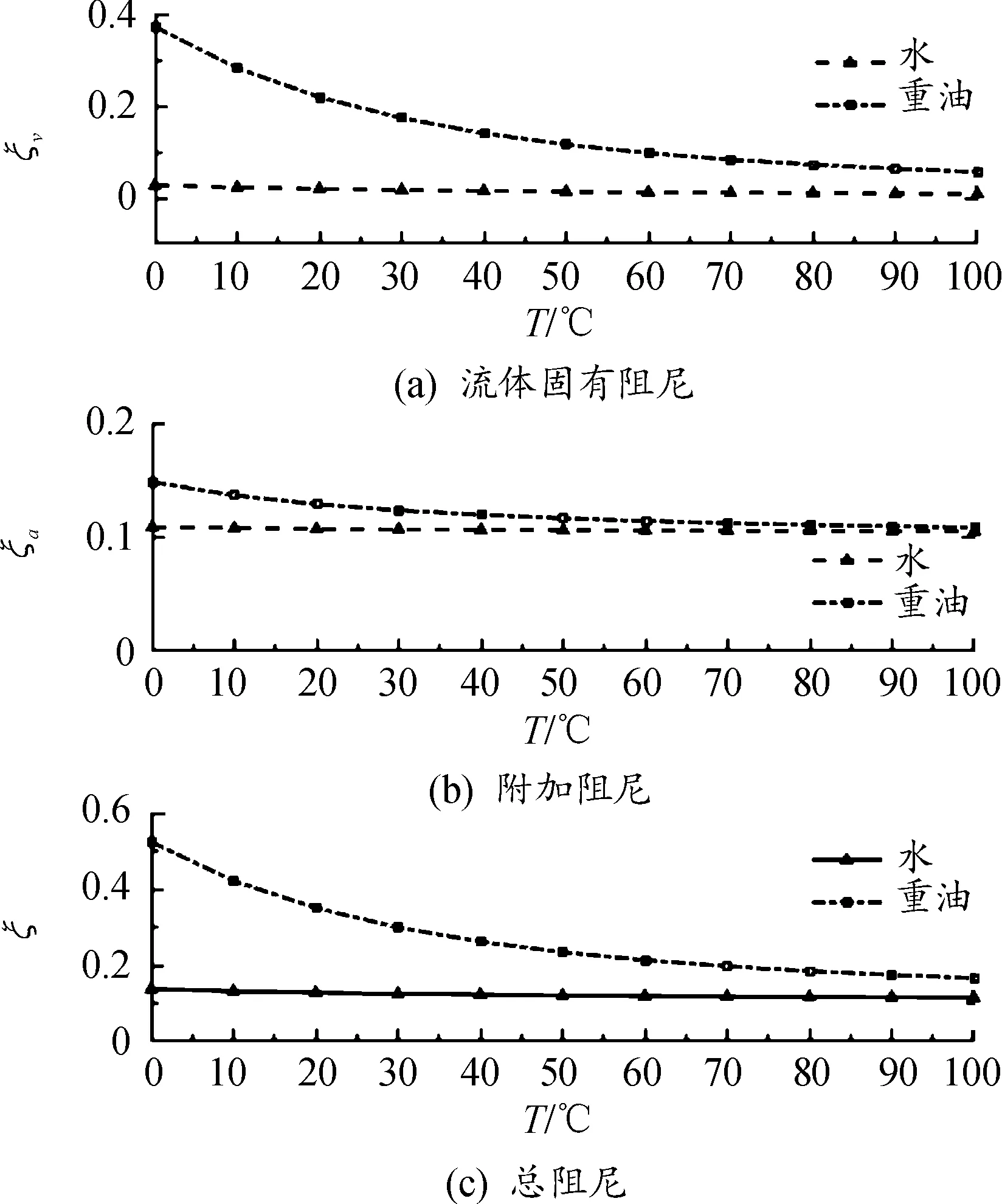
图8 不同温度的阻尼比(v=1 m/s)曲线

梁的宽度也会对梁一阶振动的阻尼比产生重要影响，如图9所示。从图中可以看出，随着梁宽度的增加，雷诺数逐渐增大，黏性效应减弱，流体本身的固有阻尼减小，而附加阻尼则随着梁宽度的增加而逐渐增大。因此，系统总阻尼随梁宽度的变化规律较为复杂，需考虑流体黏性和流动速度综合分析。如流体为100 ℃的重油时，系统总阻尼随宽度先减小后增大，最小值出现在b/δ=5时。

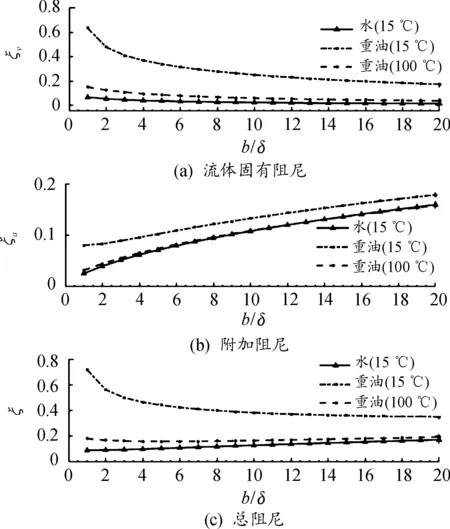
图9 不同梁宽度的阻尼比曲线(v=1 m/s)

梁的一阶振动阻尼同样随浸没深度而发生变化，如图10所示。随着流体浸没深度的增加，流体的固有阻尼和附加阻尼均逐渐增大。从图中可以看出，浸没深度对阻尼的影响规律与其对一阶固有频率的影响规律是相同的，即主要在梁的自由端产生作用。

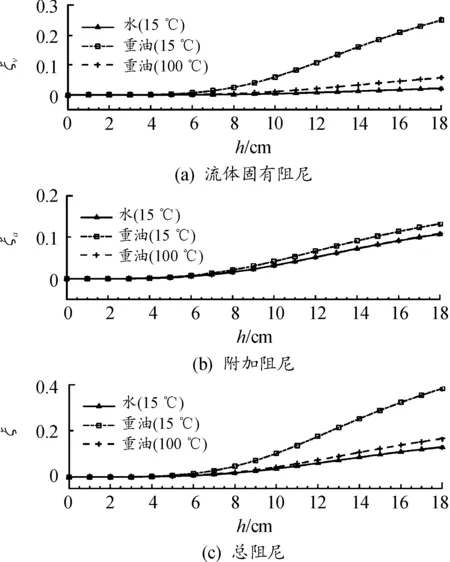
图10 不同浸没深度的阻尼比曲线(v=1 m/s)

4 瞬态响应分析

流体沿着梁长度方向上升或下降时，其频率和阻尼均随流体浸没深度发生变化，且与流体流动速度有关。尤其是流体下降时，会引发负的流体附加阻尼，产生不利影响。因此，需要对梁的瞬态域响应特性进行分析。

采用纽马克-β法求解流体下降时梁的瞬态响应。初始时刻，流体的深度h0=L。不同下降速度下，梁的位移响应和振幅时间历程如图11～13所示。

从图11、12中可以看出，当流体黏性较小时，梁的一阶固有频率随液面的下降逐渐增大，并逐渐接近或达到真空中的固有频率，且频率变化速率随流体下降速度逐渐增大。

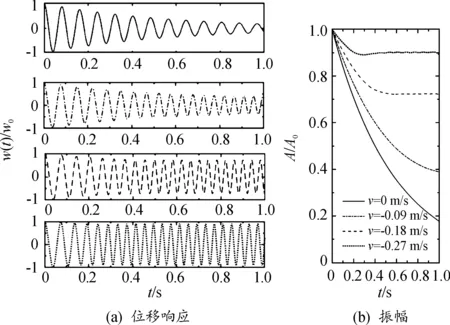
图11 不同下降速度的瞬态响应 (水,15 ℃)

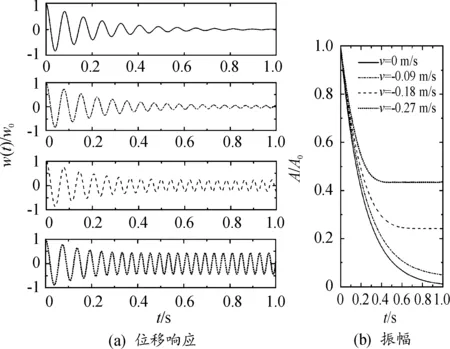
图12 不同下降速度的瞬态响应 (重油,100 ℃)

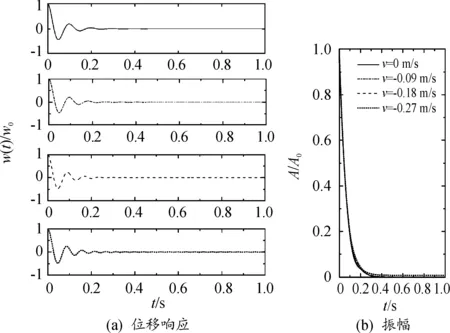
图13 不同下降速度的瞬态响应曲线 (重油,15 ℃)

随着流体的下降，流体引起的阻尼逐渐减小，振幅随时间的减小逐渐减弱。此外，流体的下降会引起负的附加阻尼，流体为水(图11)和100 ℃重油(图12)时，梁的振幅随着流体下降速度的增大而逐渐增加。从图11中可以看出，若流体下降速度继续增大，系统的阻尼将会小于零，导致梁的振动发散，危害结构安全。而对于低温时的重油，由于流体本身的固有阻尼较大，梁的振动迅速衰减，液体下降速度不大时，对梁的频率和阻尼造成的影响很小，可以忽略，梁的瞬态响应特性变化不大。

5 结论

1) 流体流动会引起附加质量、附加阻尼和附加刚度，影响系统固有频率和阻尼比。

2) 悬臂梁在时变流体中的一阶固有频率随流体流动速度增大而增大，随流体浸没深度、流体黏性和梁宽度的增大而减小;而流体运动引起的附加阻尼则随上述参数的增大而增大。

3) 悬臂梁在下降的流体中做简谐振动时，频率逐渐增大，阻尼减小，且变化率随流体下降速度的增大而增大，当流体黏性较小时，下降流体引起的负阻尼会导致梁的振动发散，对结构产生不利影响。