海底水气突涌运移规律与麻坑半径定量评价

程章，赵俞成，洪义，王立忠

(浙江大学建筑工程学院，浙江杭州，310058)

在海底大陆架斜坡环境中，天然气水合物会分解形成游离状态的水气向上突涌迁移，在海床表面形成与天然气(自由态或者溶解态)和天然气水合物有关的麻坑[1]。麻坑不仅会危害到海洋基础设施的安全，而且给海洋基础设施的选址带来困难。通过海底原位观测、声学探测和钻孔取芯等方法，RIBOULOT等[2]将海底深部流体运移形成的麻坑分为I 型麻坑和II 型麻坑这2 种。海底浅埋高压水气突涌通常形成II型麻坑[2-3]。

前人对I型麻坑的形成机制及模型预测的研究相对完善，而对于II 型麻坑的形态演变的理解不足[4-6]。RIBOULOT等[2]根据沉积物原位样本和地震反射剖面数据，提出V 形区域假说，认为在超孔压作用下聚集区前端会形成局部初始裂缝，并在压力作用下扩展，最终突涌至海床表面形成V 形麻坑。SULTAN 等[7]针对尼日尔三角洲的麻坑及水合物聚集区的地质数据，提出V 形区域内存在有大量天然气水合物和游离天然气，并认为水合物的快速生长和水合物缓慢溶解是导致II型麻坑发展的主要机制。杨志鹏等[8]认为海底陆坡上发育的一部分麻坑是地层小规模断层所致，并将其归结为断裂成因[9]。为了模拟II型麻坑的形成过程，有关学者利用等效模拟法，使用有限元软件分别模拟了麻坑的半径和水气迁移路径[2,10]。

尽管上述研究为理解II型麻坑的形态发展提供了一条重要的途径，但是它们忽略了斜坡海床中原生主应力偏转对于水气迁移路径的影响，无法准确预测现场麻坑的位置及半径，且采用传统有限元法等效模拟裂缝扩展会高估突涌路径的宽度。裂缝在土中沿裂尖的最大主应力方向扩展，而海床坡角和静止土压力系数等因素会对原生主应力偏转产生显著影响，进而影响水气突涌路径以及麻坑半径。因此，在预测浅埋高压水气突涌形成II型麻坑的扩展路径时，必须要考虑应力主轴旋转这个重要因素。

本文作者基于RIBOULOT等[2]提出的V形区域假说，首先，利用扩展有限元和Cohesive 黏聚力单元相结合的数值模拟方法，建立二维平面应变应力-渗流耦合的水气突涌模型，模拟II型麻坑的形成过程；然后，根据数值模拟结果，探究海床坡角和静止土压力系数对裂缝周围应力场、孔压场以及裂缝扩展路径的影响；最后，综合考虑海床坡角和静止土压力系数的影响，给出麻坑半径的评价方法，为海洋基础选址提供一定参考。

1 数值原理

1.1 应力-渗流耦合基本理论

饱和软黏土中的高压劈裂过程会影响土体的应力场，因此，数值模拟方法采用基于有效应力原理的应力-渗流耦合分析方法[11-12]。完全饱和的土层应力平衡方程可用虚功原理表达：一定时间内土体上的虚功等于作用在土体上的体力和面力所产生的虚功，土体的平衡方程为

式中：符号“:”为张量运算中的双点积运算；V为土体体积；σ'为土体的有效应力张量；pw为孔隙流体压力；I为二阶单位张量；δε˙虚应变率张量；S为土体表面积；t为单位面积上的外力矢量；δv为虚速度矢量；f为单位体积上的体力矢量。

对于不可压缩流体渗透通过饱和土体单元，根据连续性条件和质量守恒定律可知，单位时间内某一土体单元内流体质量的变化量与该单元流进与流出的流体质量之差相等，连续性方程可以写成

式中：t为时间；ρw为孔隙流体的密度；nw为土体的孔隙率；vw为孔隙流体的渗透速度矢量；n为面S上外法线方向的单位矢量。

1.2 扩展有限元方法

扩展有限元法(XFEM)由MOËS 等[13]提出，扩展有限元法将裂缝视为完全分离的实体，该实体独立于网格，且无需在裂缝扩展过程中进行裂尖范围的网格重划分，大幅减少了计算量。扩展有限元方法通过引入富集函数来表示不连续位移场[14]：位移不连续函数表征裂缝面所引起的位移不连续；裂尖渐进函数描述裂尖附近应力奇异场。

1.3 黏聚力单元区本构行为：裂纹萌生与扩展

模拟饱和软黏土的劈裂破坏时，Cohesive单元往往会受到3个方向的应力，采用B-K断裂准则来计算复合型裂缝的总临界应变能释放率Gc，表达式如下：

式中：Gc为复合型裂缝总临界断裂能释放率；GIc，GIIc和GIIIc分别为法向、剪切方向和扭转方向的临界断裂能释放率；η为与材料本身特性相关的参数。

B-K断裂准则和黏聚力牵引分离损伤模型描述了复合型材料的断裂行为[15-16]。图1所示为黏聚力单元损伤模型。图中δ0为单元初始损伤时对应的张开位移，δf为裂缝起裂时对应的张开位移。由图1可见：黏聚力牵引分离损伤模型主要由2个参数组成，即最大拉应力Tmax和总断裂能释放率Gc。针对各向同性的岩土材料，一般可假设3个方向的断裂能释放率相等[17]，由式(3)可得总临界断裂能释放率Gc等于I 型临界断裂能释放率GIc。基于线弹性断裂力学可得到I型临界断裂能释放率GIc与断裂韧度KIc之间的关系为

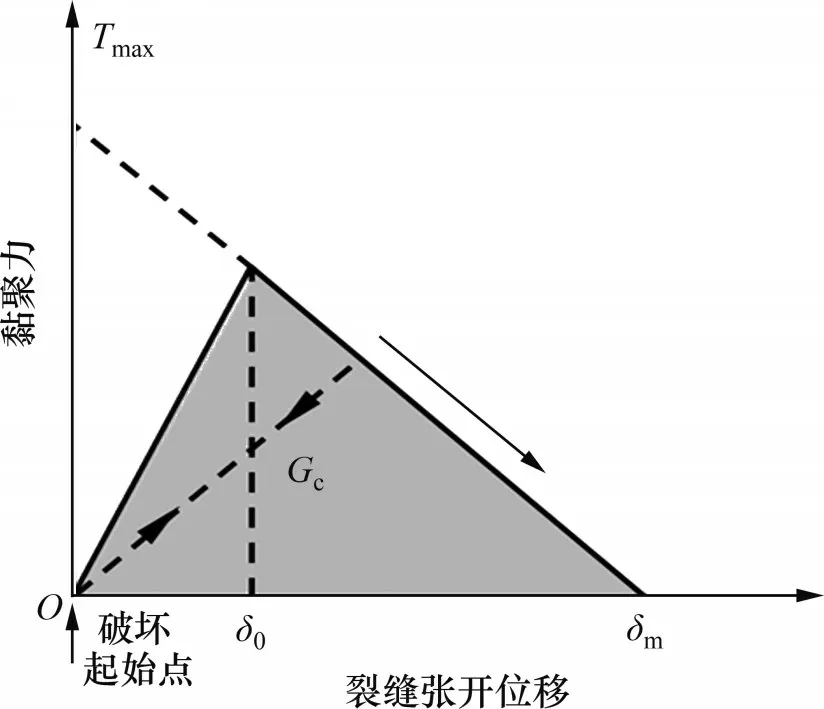
图1 黏聚力单元损伤模型[16]Fig.1 Cohesive element damage model[16]

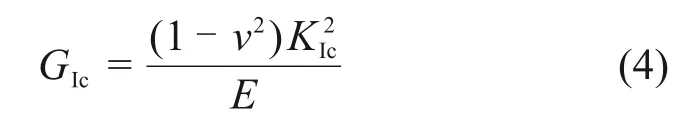
式中：GIc为I 型临界断裂能释放率；v为泊松比；KIc为I型断裂韧度；E为弹性模量。

JOHNSON 等[18]基于加拿大新斯科舍省3 个场地的现场探头测量结果，得到饱和细粒沉积物的拉伸断裂韧度KIc与强度su近似呈线性关系：

式中：su为土体不排水抗剪强度。

本研究中使用式(5)计算饱和软黏土的I型断裂韧度，并代入式(4)得到相应的断裂能释放率。

根据线弹性断裂力学(LEFM)，裂缝起裂受最大主应力控制，当最大主应力超过预定义的最大阈时，就会形成裂缝。新形成的裂缝方向垂直于裂纹尖端附近的局部最大拉应力方向。

1.4 裂缝面流体流动模型

假设Cohesive 单元内的流体是连续不可压缩的牛顿流体，流体流动可以当成顺裂缝面方向的切向流和垂直于裂缝面的法向流[19-20]。

WANG 等[21]针对不同压缩系数的裂隙流体，开展了在岩土体中的平面应变裂缝扩展模拟试验，发现流体的压缩性对岩土体中裂缝的扩展影响很小。故本研究中不考虑高压渗流破坏模拟中裂缝内流体的压缩系数，统一按不可压缩的水进行模拟。

2 海底浅埋高压水气突涌形成麻坑的扩展有限元模型

2.1 XFEM网格与边界条件

图2所示为平面应变数值模型及网格。取单位厚度的海床建立二维轴对称平面应变模型。由于麻坑是环形的，因此用轴对称的几何模型来进行数值模拟。根据现场地质数据，点划线为对称轴，模型长×宽为100 m×150 m，整体水头为500 m(以D点计)，并沿深度线性增加。其中边界AB与CD为竖向滑动边界，AD为自由边界，均分布线性孔压；边界BC竖向位移约束，边界上的孔压均匀分布。土体单元采用四节点孔压单元CPE4P 模拟。单元网格宽度为5 m，下部为规则的长方形网格。裂缝不需要划分网格。

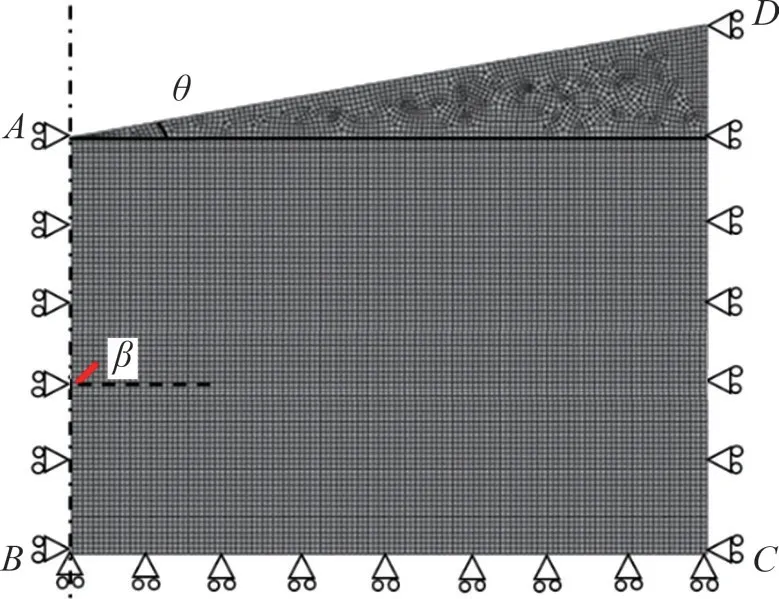
图2 平面应变数值模型及网格Fig.2 Plane strain numerical model and grid

2.2 土体本构模型与参数

初始裂缝与水平方向的夹角β在0°～45°范围内[3,22]，本研究β取45°。初始裂缝长度取10 m。天然气水合物聚集区(concentrated hydrate zone，CHZ)的埋深范围在10～800 m[22]。为了减少计算量，本研究中V 形裂缝的埋深取60 m。根据CHILLARIGE等[23]统计结果，海床坡角在0°～10°之间。故参数分析中取坡角θ为0°，2.5°，5.0°，7.5°和10.0°。

表1所示为数值模拟基本参数[17,24]。模型采用理想线弹性本构，根据弹性力学可知，静止土压力系数K0与泊松比v的关系式如下：

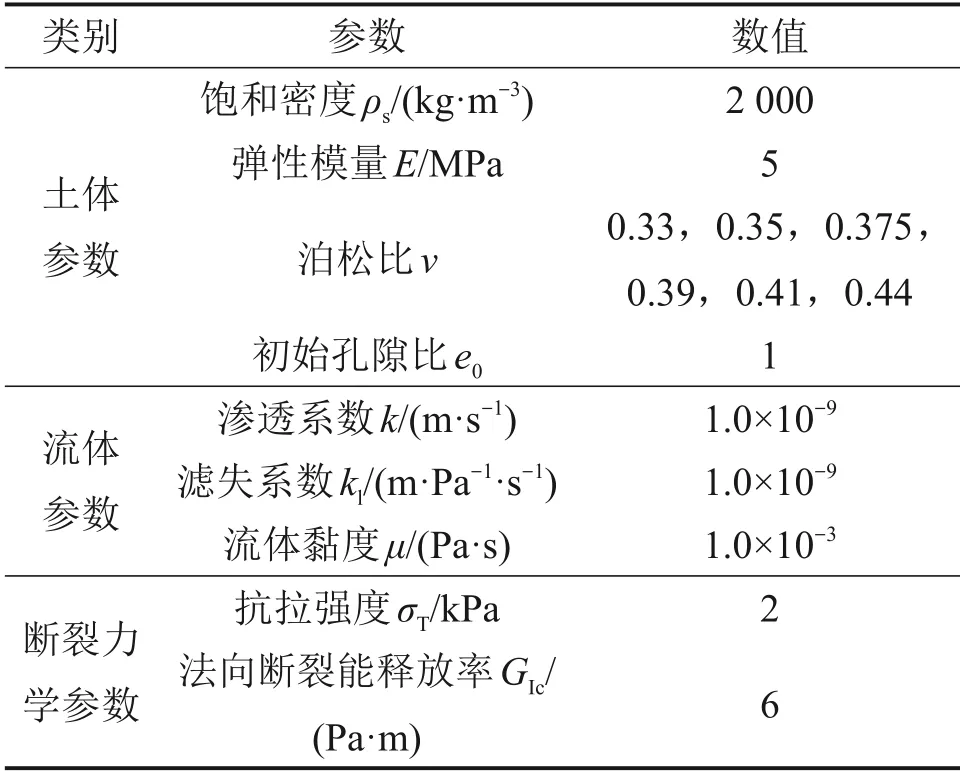
表1 数值模拟基本参数表Table 1 Basic parameters of numerical simulation

根据饱和软黏土的泊松比取值范围，参数分析中静止土压力系数K0取0.50，0.55，0.60，0.65，0.70和0.80。数值模型中土体是均质分布的，扩展有限元模型使用摩尔-库仑破坏准则和理想线弹性本构来描述每个土层的应力-应变行为。假设注入流体在裂隙内的滤失系数很小，取1×10-9。饱和软黏土的抗拉强度一般很小，可忽略不计，但为了保证数值模型的收敛性，本研究中将抗拉强度取2 kPa。由于缺少对海底饱和软黏土断裂韧度的测量，海底浅埋高压水气突涌数值模型的土体临界断裂能释放率采用半经验公式进行推算。

2.3 数值模拟步骤

在给定边界条件情况下，通过应力迭代法完成斜坡海床模型的初始地应力平衡，进而设置高压流体注入，开展扩展有限元的应力-渗流耦合分析，模拟深海浅埋高压水气突涌运移。

3 浅埋高压水气突涌过程中的裂缝扩展规律

3.1 起裂和扩展规律

图3所示为海床中不同坡角和静止土压力系数K0条件下对应的突涌起裂压力。由图3可见：在初始裂缝埋深相同的情况下，海床坡角越大，静止土压力系数越大，突涌发生所需要的压力则更大。起裂压力几乎随着静止土压力系数增大而线性增加。当坡角等于0°，静止土压力系数K0从0.5增加到0.8 时，起裂压力从510 kPa 增加到740 kPa；而当静止土压力系数等于0.5 时，坡角从0°增加到10°，起裂压力从510 kPa 增加到620 kPa。对比坡角为0°和10°工况下的初始裂缝处侧向压力可知，软黏土中的突涌起裂压力主要取决于初始裂缝所受到的侧向压力，约60%的起裂压力需用于克服侧向压力，使裂缝张开。

图3 不同工况对应的突涌起裂压力Fig.3 Initation pressure of water and gas surge under different conditions

以坡角θ为0°、静止土压力系数K0为0.55的平坡海床中浅埋高压水气突涌为例，重点分析海床中浅埋高压水气迁移过程中的应力场和孔压场分布规律。图4所示为高压水气突涌过程中土体的主应力和超孔压场分布图。由图4可见：对于平坡海床，初始地应力场沿深度递增，且最大主应力方向均为竖直方向。由于裂缝内存在流体驱动，因此，裂缝的起裂和扩展会引起周围土体的应力重新分布，最大主应力方向发生旋转。裂缝扩展沿着裂尖单元的最大主应力方向，裂缝两侧的土体受到流体挤压的作用，产生正超孔压，裂尖附近的土体由于受拉作用会产生负超孔压。同时，最大主应力方向逐渐变为水平方向，但离裂缝较远处的土体应力并未发生改变，最大主应力方向仍为竖直方向。由于裂缝扩展过程中土体应力主轴旋转，最终浅埋高压水气突涌路径和初始地应力场存在夹角。

图4 水气突涌主应力和超孔压分布规律Fig.4 Principal stress and pore pressure distribution of water and gas surge

3.2 静止土压力系数和海床坡角对麻坑半径的影响

图5(a)～(d)所示为坡角为0°，静止土压力系数分别为0.8，0.7，0.6 和0.5 的平坡海床中浅埋高压水气突涌路径和最大主应力矢量图。由图5(a)～(d)可见：静止土压力系数为0.8时，裂缝的扩展方向会更加接近水平，浅埋高压水气突涌路径更长，形成的麻坑半径也更大，半径几乎达到100 m，此时裂缝扩展对周围土体应力的影响范围也更大。

图5(d)～(f)所示为K0为0.5，坡角分别为0°，5°和10°这3 种工况下海床中浅埋高压水气突涌路径和最大主应力矢量图。由图5(d)～(f)可见：坡角为10°时，裂缝整体的扩展方向更趋近于水平，导致水气突涌形成的麻坑半径更大，达到80 m左右。

图5 水气突涌扩展路径及最大主应力矢量图Fig.5 Propagation path and maximum principal stress vector of water gas surge

无论是平坡海床还是斜坡海床，裂缝趋向于沿裂尖的最大主应力方向扩展。由于裂缝内存在流体驱动，裂缝的起裂和扩展会引起周围土体的应力重新分布，最大主应力方向发生旋转，并随着裂缝扩展逐渐趋于水平，但离裂缝较远处的土体应力并未发生改变。由于裂缝扩展过程中土体应力主轴旋转，最终导致浅埋高压水气突涌路径和初始地应力场之间存在夹角。

图6所示为麻坑半径与静止土压力系数、海床坡角的关系图。由图6可见：静止土压力系数越大，海床坡角越大，对应海床的初始最大主应力方向的倾斜程度更大，导致裂缝扩展更加趋近于水平。对比坡角对于麻坑半径的影响，可以发现静止土压力系数对麻坑半径的影响程度更大。

图6 麻坑半径与静止土压力系数和海床坡角的关系图Fig.6 Relationship of pockmarks radius with coefficient of earth pressure and seabed slope angle

3.3 麻坑半径综合评价

图7所示为麻坑半径的综合评价图。由图7可见：麻坑半径与海床坡角、静止土压力系数呈正相关。海床坡角越大，静止土压力系数越大，则形成的麻坑半径越大，浅埋高压水气突涌影响的范围越大。取坡角等于2.5°时，当静止土压力系数K0从0.5 增加到0.8，麻坑半径从72 m 增加到105 m；取K0为0.6，当坡角从0°增加到10°，麻坑半径从72 m增加到96 m。

图7 麻坑半径综合评价图Fig.7 Comprehensive evaluation of pockmark radius

罗敏等[25]调研发现海底绝大多数的麻坑直径落在75～200 m 的区间内。PILCHER 等[26]统计世界各地已观测到的57 个麻坑区，发现大部分麻坑直径处于50～270 m 的区间。数值模拟结果表明，麻坑的直径主要在140～230 m之间，与前人的统计研究结论相一致。

4 结论

1)静止土压力系数与海床坡角影响应力主轴旋转，进而影响突涌路径。海床坡角越大，静止土压力系数越大，土体应力主轴越易发生旋转，则浅埋高压水气突涌形成的麻坑半径也越大，影响范围越大。

2)静止土压力系数对浅埋高压水气突涌路径的影响比坡角的影响更大。当坡角等于0°，静止土压力系数从0.5 增加到0.8 时，麻坑半径从70 m增加到100 m；而当K0为0.5，坡角从0°增加到10°时，麻坑半径从70 m增加到80 m。

3)在初始裂缝埋深相同的情况下，起裂压力随着静止土压力系数和坡角增大而增加，其中静止土压力系数的影响更大。当坡角等于0°，静止土压力系数K0从0.5 增加到0.8 时，起裂压力从510 kPa 增加到740 kPa；而当静止土压力系数等于0.5，坡角从0°增加到10°时，起裂压力从510 kPa增加到620 kPa。

4)应力-渗流耦合分析方法结合了扩展有限元与Cohesive 黏聚力单元，能够考虑地层原生主应力影响，即静土土压力系数和海床坡角的影响，模拟出水气突涌过程中的运移路径以及应力场、孔压场变化，实现水气突涌运移过程的模拟以及对形成的麻坑半径进行综合评价。