地应力对巷道布置的影响——以淮南矿区为例

夏 磊，刘启蒙，柴辉婵，谢志钢，周晓芳

(安徽理工大学 地球与环境学院，安徽 淮南 232001)

1 引言

地应力是一种相对稳定的天然应力场，客观存在于地层中。但同时，地应力场也具有非稳定性，是复杂多变的。地应力由地层的浅层向深层的过程中，呈现出一定的规律性变化，如地应力增大、岩石产生塑性软化且较易破碎的现象等[1]。在煤炭开采中，地应力对于巷道的稳定性的影响，国内外学者对其进行了大量的研究，提出了多种巷道支护的方法[2]，并给出了合理布置巷道与最大水平主应力夹角理论指导[3]，但是对于巷道轴向方向与最大、最小主应力的夹角的规律与选择仍然需要进一步的研究。本文通过对淮南各个矿区的共86组地应力数据的统计与分析，简要得出巷道的最优布置方位与最大主应力夹角的规律。

2 地应力对巷道布置的影响

2.1 地应力数据

通过查阅文献、对矿井资料整理以及现场实测采集，得到淮南煤田各个矿区不同位置处地应力数据共计86组。其中，新集矿区30组，潘一矿6组，顾桥矿20组，望峰岗矿8组，潘三矿3组，潘北矿3组，谢一矿3组，丁集矿2组，张集矿2组，潘二矿4组，新庄孜矿4组，刘庄矿1组。对最大水平主应力、最小水平主应力以及垂直主应力间的相对大小关系进行分析，发现σH>σh>σv类型的数据有12组，埋深范围350.7～820 m，平均埋深556.35 m，占统计数据组数的14.0%；σH>σv>σh类型的数据有55组，埋深范围370～1076 m，平均埋深750.78 m，占统计数据组数的64.0%；σv>σH>σh类型的数据有19组，埋深范围440～1150 m，平均埋深706.25 m，占统计数据组数的22.1%。可以看出，在淮南地区已开采深度范围内构造应力场起主导作用。

2.2 巷道最佳布置角度分析

利用钻井水力压裂法和应力解除法获得地应力数据后，一般采用测压系数λ1、λ2(λ1=σH/σv，λ2=σh/σv)对地应力场进行描述[4]。依据最大水平主应力与垂直应力间的比值关系分类，当λ1<1时，最大水平主应力小于垂向应力，煤层总体以垂向上压应力为主，水平方向则以拉伸应力为主，具有大地静力场特征；当λ1>1时，最大水平主应力大于垂向应力，煤层总体以水平向上压应力为主，具挤压型应力场特征；当λ1≈1时，则地应力场接近静水压力场。

从地应力场的角度考虑巷道布置时，必须考虑巷道轴线方向与最大主应力方向的夹角，最优夹角应使作用在巷道围岩边界上的法向应力和垂直主应力满足：

σn/σv=1

(1)

式(1)中，σn为法向应力，σv为垂直主应力。

由前文分析可知，淮南煤田已开采范围内，σH>σv>σh类型应力场占大多数。在σH>σv>σh类型中，σ1=σH，σ2=σv，σ3=σh，在这种原岩地应力场中，选择合适的巷道方向，巷道围岩边界上的法向应力和垂直主应力可以满足σn/σv=1=1。任意斜面上的法向应力与最大和最小水平主应力的关系为：

(2)

式(2)中，α为巷道轴线与σH方向的夹角[5]。把σn=σv代入式(2)得到：

(3)

求解式(3)，可得到最优夹角α0[6]，即：

(4)

3 数据分析

(1)由式(4)可以看出，在σH>σv>σh类型地应力场中，巷道轴线方向与σH方向的最优夹角的变化范围为0°<α0<90°。根据统计的数据，对淮南煤田σH>σv>σh类型应力场下最优巷道布置方位进行计算，结果见表1，α0与λ1的关系见图1。

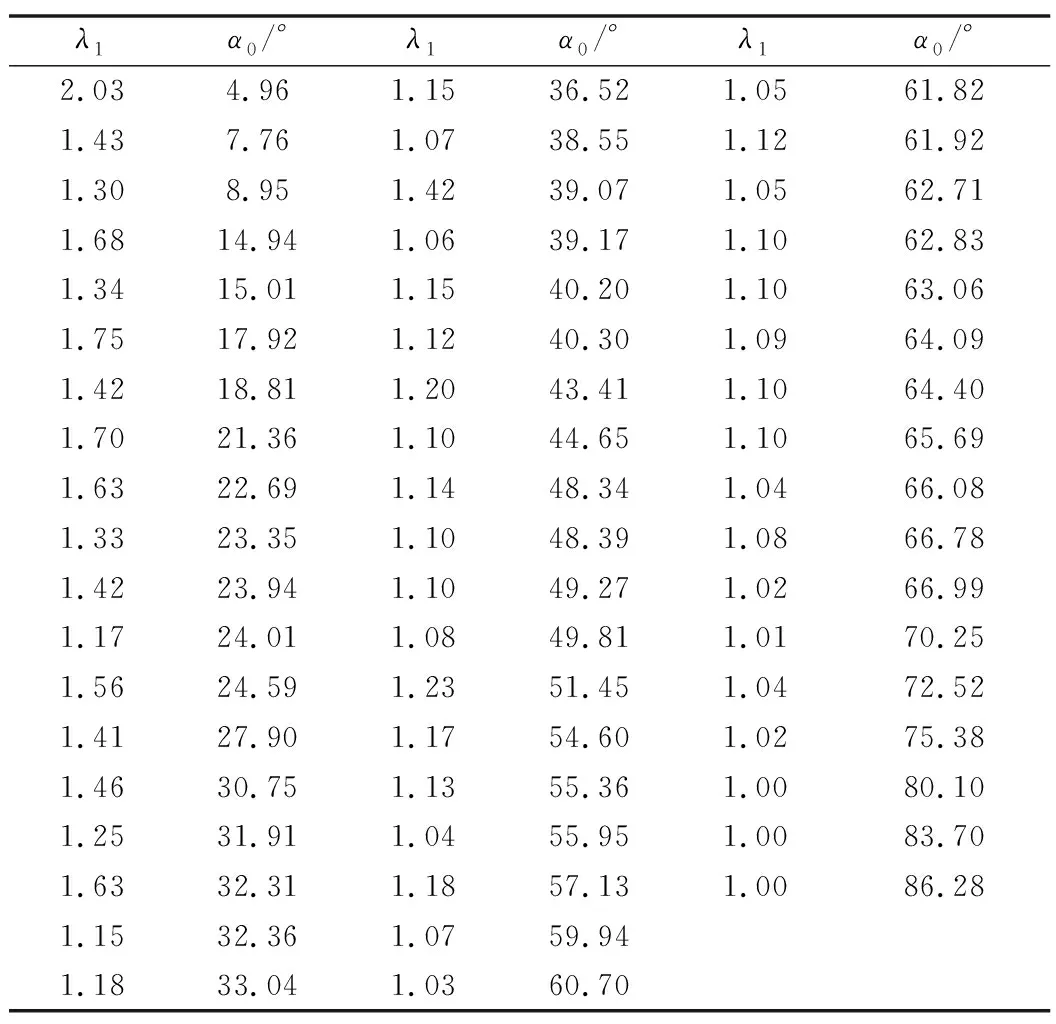
表1 α0与λ1关系

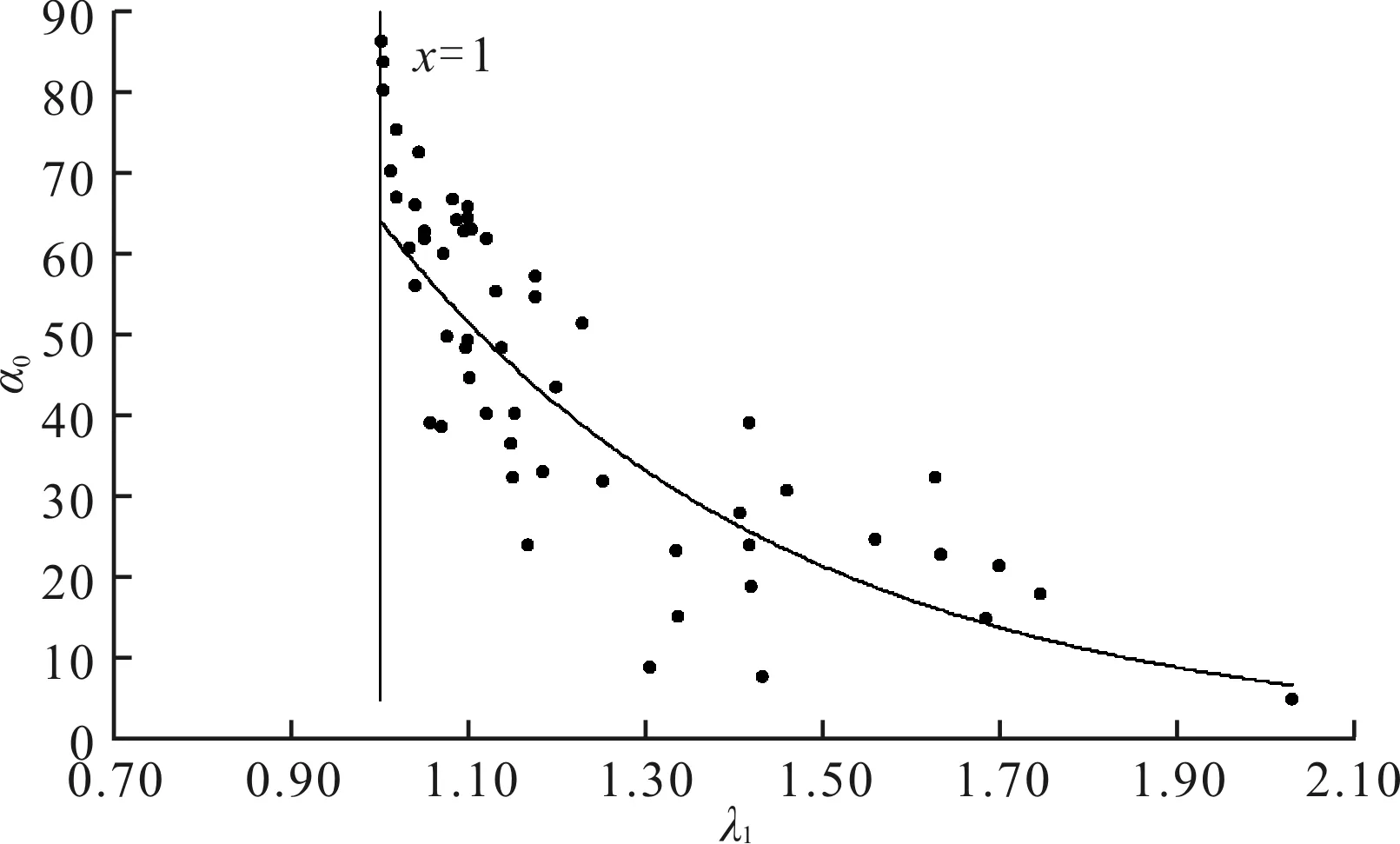
图1 α0与λ1关系

由图1可看出，巷道最优布置方位主轴线与最大水平主应力的夹角α0随最大水平主应力和垂直主应力的比值λ1的增大而发生指数型降低，二者的拟合公式见式(5)。这一现象说明随着最大水平主应力的相对增大，水平方向的应力对巷道布置的影响逐渐超过垂直应力，最优布置巷道的轴线偏向最大水平主应力的方向；当σH≈σv时，巷道的最优布置方位垂直于最大水平主应力。

α0=68.682×λ1-2.994

(5)

式中，确定系数R2=0.6786。

(2)根据式(5)，当σH>σh>σv时，根据统计的数据，对淮南煤田σH>σh>σv类型应力场下最优巷道布置方位进行了计算，α0与λ2的计算结果见表2，两者的关系见图2。

由图2可以看出巷道最优布置方位主轴线与最大水平主应力的夹角α0随着最小水平主应力σh和垂直主应力σv的比值有着线性增长的关系。这一现象说明：随着最小水平应力σh的相对增大，垂直方向的应力对巷道布置的影响超过水平应力，最优布置巷道的轴线偏向垂直主应力的方向，当最小水平主应力σh和垂直主应力σv近似相等时，即σh≈σv，巷道的最优布置方位近似平行于最小水平主应力。

α0= 115.3λ2-103.8

(6)

其中确定系数R2=0.737。

表2 α0与λ2关系

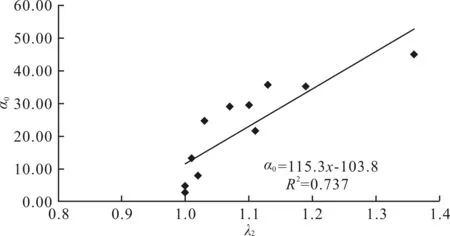
图2 α0-λ2 关系

(3)根据式(4)，当σv>σH>σh时，根据统计的数据，对淮南煤田σv>σH>σh类型应力场下最优巷道布置方位进行计算，去除无效数据之后，α0与λ1的计算结果见表3，两者的关系见图3。

表3 α0与λ1关系表

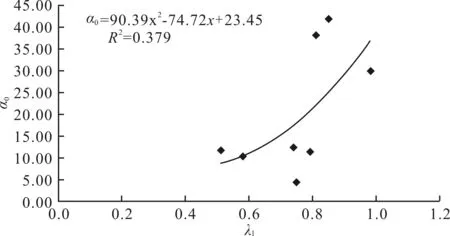
图3 α0与λ1关系

由图3可以看出，巷道最优布置方位主轴线与最大

水平主应力的夹角α0随最大水平主应力和垂直主应力的比值λ1的增大呈现二次增加的趋势。二者的拟合公式见式(7)，这一现象说明：在最大应力为垂直应力的情况下，随着最大水平主应力的相对增大，垂直方向的应力对巷道布置的影响逐渐超过水平应力，最优布置巷道的轴线偏向垂直主应力的方向，当σH≈σv时，巷道的最优布置方位与最大水平应力约成45°夹角。

α0=90.39λ12-74.72λ1+23.45

(7)

其中确定系数R2=0.379。

4 结论

(1)根据有统计的86组地应力数据，64%的地应力数据符合σH>σv>σh的特征，平均埋深约为750.78 m，应力量级以中等和高应力区为主，合计约占91.7%。

(2)在σH>σv>σh类型地应力场中，随着最大水平主应力的相对增大，布置巷道时，巷道的轴线方向应向最大主应力方向靠近，且当最大主应力近与垂直主应力相等时，巷道的布置方向应与最大水平主应力垂直。

(3)在σH>σh>σv类型地应力场中，随着最小水平主应力的相对增大，布置巷道时，巷道的轴线方向应向垂直主应力方向靠近，且当最小水平主应力近似与垂直主应力相等时，巷道的布置方向应与最下水平主应力近似平行。

(4)在σv>σH>σh类型地应力场中，随着最大水平主应力的相对增大，巷道布置时，巷道的轴线方向应向垂直主应力方向靠近，且当最大主应力近似与垂直主应力相等时，巷道的布置方向应与最大水平主应力约成45°夹角。