开挖扰动诱发主应力轴偏转下软岩力学试验研究

张向东，张雪峰，刘家顺，李 军

（辽宁工程技术大学 土木工程学院，辽宁 阜新 123000）

0 引言

深部开采过程中，围岩应力场重新调整将改变岩体原有的应力状态和应力路径，影响围岩力学响应、裂隙扩展方向和扩展深度，甚至产生裂缝贯穿进而引发地下硐室失稳、基坑失效和滑坡等工程灾害.谢和平等[1-2]呼吁发展采动岩体力学，考虑原位应力状态和开采应力路径的影响，创立新的过程行为力学理论，将工程扰动过程与岩体力学响应相结合展开研究.

大量学者对岩石在开采扰动作用下变形特性进行了试验及理论研究，以往的研究一方面是借助三轴仪，开展常规三轴加卸载试验，其核心目的是研究岩石加卸荷过程中的破坏机制[3-4]、力学强度参数损伤劣化效应及其卸荷破坏的强度特性[5-6]，通过加卸载试验提出了新的卸荷力学描述参量[7-8]，为软岩岩体的稳定控制提供了力学强度准则[9-11].另一方面，国内外学者采用数值模拟对地下工程开挖掌子面掘进过程中围岩的复杂应力路径和破坏模式进行探讨[12]，研究了开挖面周围主应力发生旋转引起的围岩应力和变形的变化规律，在地下工程开挖掘进过程中，开挖应力状态及不同应力状态之间的相互转换是围岩发生周期性破断的力学根源，直接影响围岩的稳定性及其破坏过程[13-16].

综上，在地下洞室开挖过程中，开挖卸荷打破了岩体结构系统原有的平衡，致使围岩内部应力场重新分布，开挖扰动产生的应力路径不仅包括应力大小的改变，还包括应力方向的旋转[17-20]，从而影响围岩裂纹发育、变形量及变形速度，甚至引发围岩失稳等工程灾害[21].但前述研究均未考虑地下工程开挖扰动诱发的主应力轴旋转应力路径对软岩强度和变形特性的影响.因此，以西部地区弱胶结软岩为研究对象，利用空心扭剪试验系统，针对地下工程开挖过程中的应力路径进行主应力单调变载试验，研究偏应力大小和应力主轴旋转耦合协调改变过程中弱胶结软岩轴向变形特性和强度特性，为进一步优化地下工程设计提供理论依据.

1 试验方案

1.1 试验岩样基本特征

岩样取自内蒙古红庆梁煤矿主斜井，进行弱胶结软岩试样膨胀性试验、耐崩解试验、单轴抗压强度试验等，得到岩石的物理参数，见表1.

表1 试验岩样物理参数Tab.1 physical parameters of test rock sample

空心圆柱试样外径为100 mm，内径为60 mm，高度h为200 mm.由于原状弱胶结软岩岩样强度低，用切土器和削土刀加工制作即可.试样制作及安装过程见文献[20]，安装后的试件见图1.

图1 安装后试样Fig.1 installed samples

1.2 试验设备

GDS空心圆柱试验硬件主要包括：①轴向、扭转驱动装置和压力室顶盖；②围压控制器、反压控制器、内压控制器；③信号调节装置/数字式传感器接口单元（DTI）；④ GDSDCS 控制板，见图2.

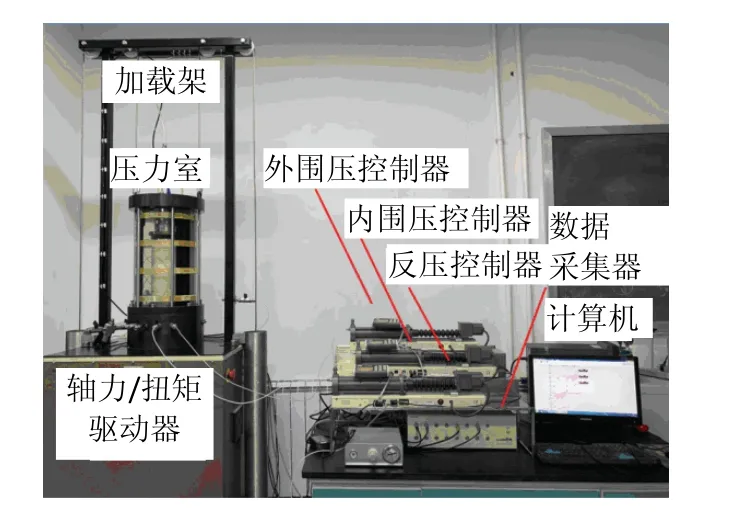
图2 GDS空心圆柱试验系统Fig.2 GDS hollow cylinder test system

GDS空心圆柱试验系统是直接通过数字伺服独立控制空心圆柱试样的轴向力W、扭矩MT，以及土样的外压P0，这3个力学加载参数控制试样中土体单元受到的轴向应力、切向应力、径向应力、剪应力.基本应力状态及对应的应变状态见图3.

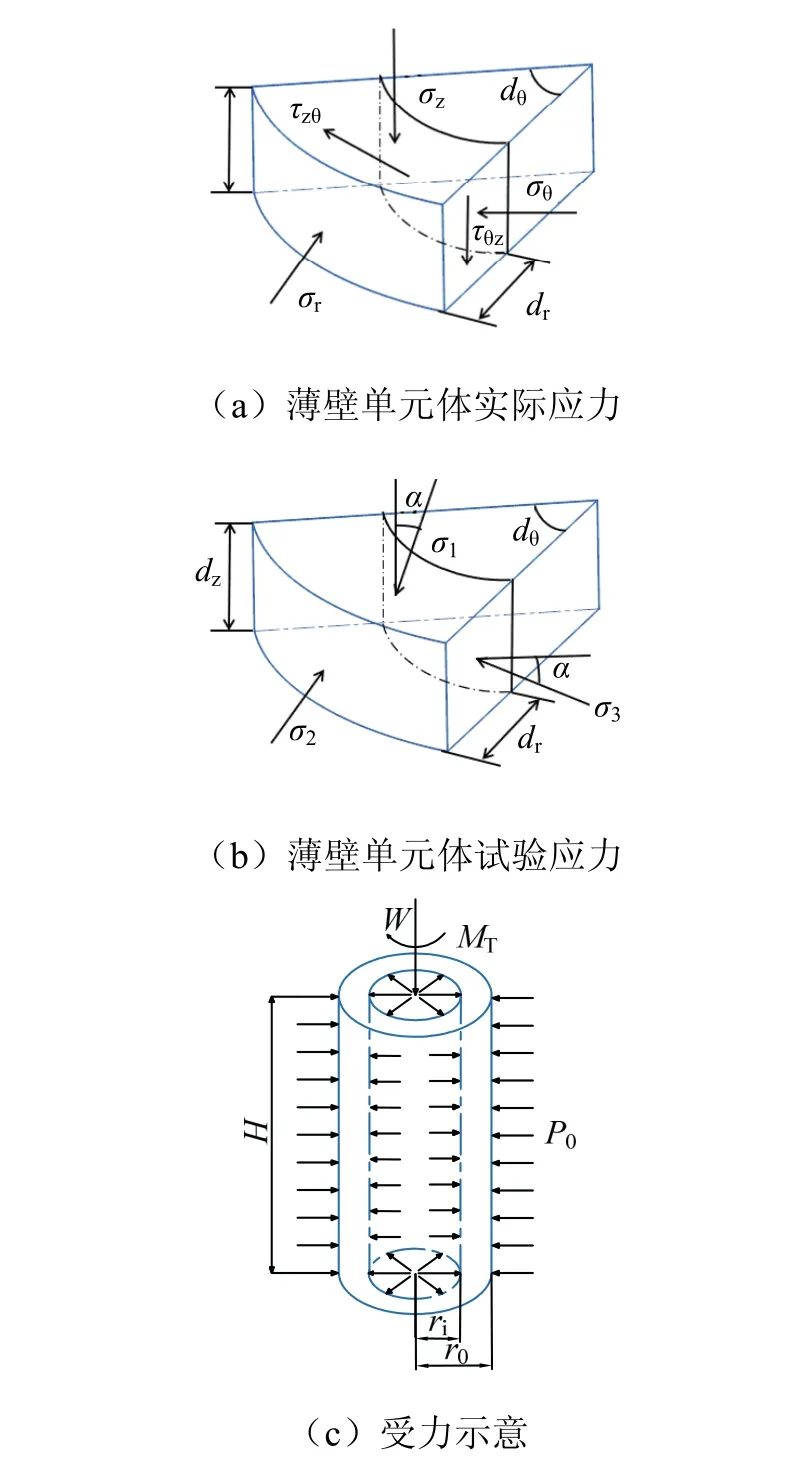
图3 空心圆柱试样示意Fig.3 schematic of hollow cylindrical specimen

主应力轴旋转试验过程通过独立控制平均主应力、偏应力、主应力旋转角实现，各参数定义为

式中，p为平均主应力，MPa；q为偏应力，MPa；σ1、σ2、σ3分别为大主应力、中主应力、小主应力，MPa；σz、σr、σθ、τzθ分别为轴向应力、径向应力、环向应力、剪应力，MPa；α为主应力旋转角，°.

通过对空心试件施加独立控制的轴力、扭矩和内外压力来实现对应力参数p、q和α的控制.

1.3 试验加载方案

工作面掘进过程中围岩监测点主应力[12]见图4.

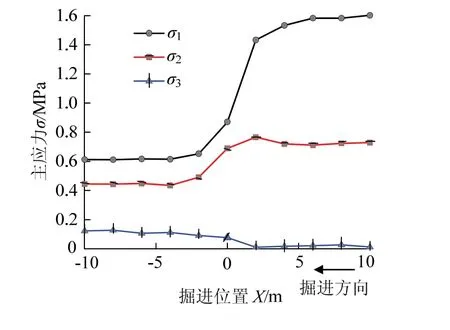
图4 掌子面掘进过程监测点主应力Fig.4 monitoring point main stress of palm surface excavation process

由图4可知，在掌子面掘进过程中，σ1、σ2逐渐减小，σ3逐渐增大.通过σ1、σ2和σ3计算出平均总主应力和偏应力.掌子面附近最大旋转角度仅为3.8°，大主应力的方向几乎没有旋转；而中主应力有一定程度的旋转，最大旋转角度为35°，表明应力旋转主要位于掌子面前方，所以试验中将主应力轴旋转角设置为35°.

为研究在主应力轴旋转条件下软岩的应力应变变化规律，将平均总主应力设置为1 MPa，偏应力分别设置为0.15 MPa、0.3 MPa、0.45 MPa、 0.6 MPa、0.75 MPa、0.9 MPa，试验加载过程中主应力轴旋转速率为1 °/min，主应力轴旋转角变化范围为0°～35°，试验方案见表2.

表2 主应力轴旋转试验方案Tab.2 test scheme of principal stress axis rotation

根据表2主应力轴旋转试验方案，绘制不同试验的应力路径，见图5.

由图5可知，不同偏应力下，主应力轴旋转应力路径图是以坐标原点(0，0)为圆心，偏应力的一半为半径的同心圆，随着偏应力的增大，试验应力路径图曲线半径逐渐增大，且主应力轴旋转的应力路径的实现与平均主应力无关.

图5 不同偏应力q下的应力路径Fig.5 stress paths under different deviator stresses q

2 试验结果分析

2.1 主应力旋转角与应变关系

图6为不同偏应力作用下弱胶结软岩试件各向应变分量随主应力轴旋转角变化.由图6可知，弱胶结软岩试件在纯主应力旋转条件下，轴向和环向均产生了不可恢复的塑性变形，主应力方向从0°～35°旋转期间，轴向应变主要表现为压应变，环向应变主要表现为拉应变.

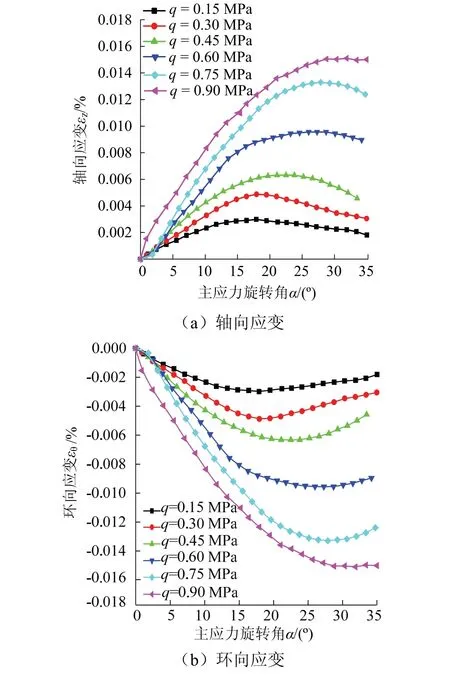
图6 弱胶结软岩不同偏应力q下的各应变分量随α变化Fig.6 variation of strain components with α in weakly cemented soft rock under different deviator stresses q

由图6（a）可知，主应力轴旋转角相同时，偏应力水平越高，轴向形变量越大.主应力轴从0°～35°旋转过程中，不同偏应力作用下的轴向应变均表现为先增大后减小的趋势.其中，偏应力水平越高，轴向应变由增大到减小时转折点处对应的主应力轴旋转角越大，即在不同偏应力作用下，轴向应变的变化趋势随主应力轴的旋转有一定的滞后性.轴向应变始终为正值，主应力轴旋转全过程轴向应变表现为压应变.

由图6（b）可知，不同偏应力条件下，试样的环向应变与轴向应变大小相同，方向相反，因为主应力轴旋转平面为轴向力与环向力所在平面（垂直于径向力方向），主应力轴旋转初期，大主应力与轴向力方向一致，使得试样轴向受压，环向相对受拉，随着主应力轴不断旋转，大主应力与环向力方向逐渐一致，试样轴向产生受拉趋势，环向产生受压趋势，但是旋转全过程环向应变表现为拉应变.q为0.15 MPa时，应变为-0.002%，q为0.9 MPa时，应变为-0.015%，随着偏应力q的不断增加，试样环向受拉也会增大.

由图6（c）可知，偏应力较小时，剪应变受主应力轴旋转角的影响相对较小，剪应变最终趋于稳定，产生不可恢复的塑形变形；偏应力较大时，剪应变随主应力轴旋转角的增大，基本呈线性增加.试验初始阶段，不同q值下剪应变都为0，且q值越大，剪应变速率发展越快.

由图6（d）可知，试件的体应变εv基本随着大主应力旋转角α的增大而增加（试件的体应变直接由GDS空心圆柱试验系统测出）.主应力轴旋转全过程，体应变剪缩为正，剪胀为负.因此试件处于剪缩状态，未发生剪胀变形.可以看出主应力轴旋转角度α在0°～5°旋转时，偏应力对体应变的影响很小；α为5°～25°时，体应变随着主应力轴旋转角不断增大而增加，且增长速率最快；α为25°～35°时，试样体变逐渐趋于稳定.体应变同样受应力的影响明显，在高应力水平下，体应变最大可达0.035%.

综上所述，主应力轴旋转过程中，弱胶结软岩会有应变累积.试件累积塑性应变的增长是不可忽略的，在地下开挖支护设计与施工过程中，必需重视各应变分量.

2.2 剪应力-剪应变关系

图7为应力路径模拟试验中剪应力与剪应变的关系，不同偏应力作用下，弱胶结软岩的剪应力-剪应变曲线表现为较好的一致性，随着剪应变增加，剪应力增大.在初始加载阶段，偏应力较小，剪应力随变形的增长相对缓慢，弱胶结软岩中原生的孔隙结构被压密，孔隙被压缩变小.试件剪应力-剪应变曲线呈线弹性变化，试件进入线弹性阶段，剪应力-变形为线性增长.如图7所示，低应力下试样的应力-应变曲线不再变化，高应力试件应力-应变曲线呈非线弹性变化，试件进入屈服阶段，此时试件变形包括弹性变形和塑性变形，直至应力达到峰值.主应力轴在0°～35°旋转的过程中，偏应力p为0.15 MPa时，剪应变可达到0.06%，p为0.9 MPa时，剪应变为0.78%.

图7 应力路径模拟试验中不同偏应力q的剪应力-剪应变Fig.7 shear stress-strain with different deviator stresses q in stress path simulation test

2.3 剪应变数学公式

由图7可知，主应力轴旋转角α是影响弱胶结软岩剪应变γzθ大小和发展规律的主要因素.当偏应力q相同时，α越大，γzθ越大；当α相同时，q越大，γzθ越大.在岩土塑形理论中，γzθ可表示为

式中，Gp为压缩模量，GPa；Gs为弹塑性剪切模量，GPa.

由于在弹性状态下当Gp趋于∞，Gs与G相等，所以剪应变只与剪应力τzθ有关.定义纯剪应力为τs，也称剪应力强度，纯剪时σ1=τzθ＞0，σ2=0，σ3=-τzθ.偏应力q用第二分量的第二不变量 2J表示.由此得

Monismith提出的幂函数模型[22]为

式中，γzθ为剪应变；2J为偏应力，MPa；A、B为拟合系数.

在不同主应力旋转角下弱胶结软岩剪应变γzθ与偏应力 2J关系曲线仍符合Monismith幂次函数模型.经过对7组试验结果的数据处理，得到拟合系数A和B与主应力旋转角的函数关系式为

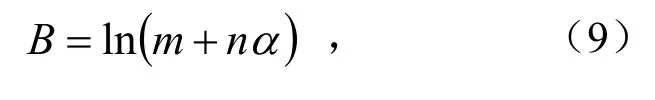
式中，a、b、m、n、k为拟合系数.

为建立考虑主应力旋转条件下弱胶结软岩剪应变与偏应力数学公式，在式（8）和式（9）中引入表征主应力轴旋转的旋转角，经对试验数据处理后得

将式（10）和式（11）代入式（7），可得到同时考虑主应力轴旋转角和偏应变的弱胶结软岩剪应变为

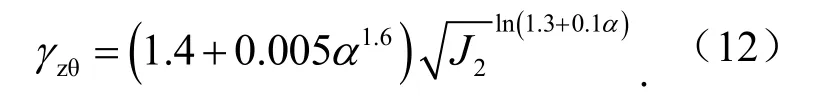
由式（12）求主应力轴旋转下弱胶结软岩的剪应变，将计算结果与试验值对比，结果见图8.

图8 不同主应力轴旋转角α下剪应变计算值与试验值对比Fig.8 comparison of calculated and experimental shear strains under different rotation angles of principal stress axes α

由图8中可知，式（12）计算的剪应变与主应力轴旋转试验的剪应变，在主应力轴旋转角较小时，结果较为接近.在α取30°～35°时，试验结果与计算值产生偏差，这是因为随着主应力轴的旋转，弱胶结软岩试件产生脆性变形，试样不再是连续介质，造成计算值与试验值有所偏差.

3 结论

（1）利用现场采集的岩样以及掌子面掘进过程中的主应力量值及方向，简化应力路径，结合主应力轴旋转试验，绘制不同偏应力下的应力路径. 随着偏应力的增大，试验应力路径图曲线半径随着 增大，且与平均总主应力无关.

（2）在主应力轴旋转的过程中，偏应力和主应力轴旋转角对岩样的轴向应变、环向应变、剪切应变、体变形发展有一定的影响；其中偏应力对各应变分量的影响较大.主应力轴旋转过程中，即使应力水平保持不变，弱胶结软岩变形依旧随着主应力轴角度的增加逐步累加.

（3）不同偏应力的6组试验所表现的应力-应变关系较类似，随着主应力轴旋转角不断增大，剪应力和剪应变越来越大.当偏应力为0.90 MPa时，剪应力最大可达到0.58 MPa.试件发生塑形破坏，应力应变曲线呈下降趋势.

（4）建立了考虑主应力轴旋转角影响的弱胶结软岩的剪应变数学方程，并对模型的可靠性进行了分析和验证.模型可以准确地确定不同旋转角和偏应力对弱胶结软岩剪应变的影响，从而确定出软岩的应变变化规律.