倾斜海床对水平电偶极子水下电场分布的影响*

焦达文 齐嘉慧 陈思迪 吴云超 陈 醒

（大连测控技术研究所 大连 116013）

1 引言［1～4］

海床是海水覆盖下的固态地球表面形态的总成，倾斜海床是指海床平面有一定倾角的海床。从地理学家的测量可知几乎绝大多数海床并不是完全平坦的，很多区域存在复杂的地形起伏，在浅海海洋环境中，水深一般在200m以内，坡度一般不超过10°。对于海床倾斜度非常小的大区域的水下电场分布，采用简化的平面海床模型是合适的；但对于海床倾斜度大的水下电场分布问题，海床地形会对电场的分布产生较大影响，需要考虑海床地形的影响。因此，本文利用COMSOL Multiphysics有限元软件对空气-海水-倾斜海床三层电场模型进行仿真计算，研究倾斜海床三层导电媒质环境中场源水下电场分布特性。

2 基本理论［5～13］

在传统的理论模型中，我们通常将浅海海洋环境简化为空气-海水-海床三层模型。浅海环境三层模型中以偶极子为典型场源，构建了三层均匀分层模型中电磁场在海水、空气以及空气-海水、海水-海床界面的分布数学模型，如图1所示。

图1 三层模型示意图

2.1 基本方程

在运用节点有限元求解电磁场边值问题时，存在界面法向不连续的问题，如果忽略这一问题去求解电磁场，往往得到不正确的解。本文运用间接方法求解电磁场，即通过求解电场场源在三维介质中的电磁场的位势，进而得到电磁场值。由电流源引入矢量位A是这样引入的：∇·B=0，利用恒等式∇·∇×A≡0，可令：

电流源区域麦克斯韦方程为

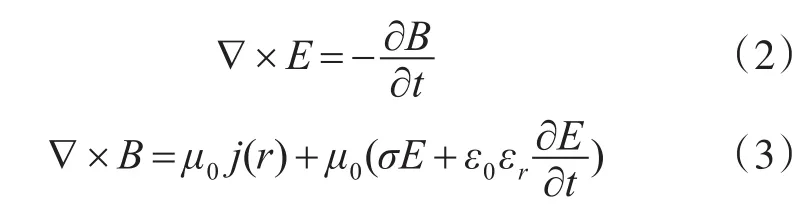
其中j(r)是电偶极子的电流密度，当Δs→ds时，j(r)=Idsδ(r)，其中δ(r)为单位阶跃函数，其意义是长度为Δs的小电流元表示无穷小电偶极子。

根据上式（2），引入标量函数V，有

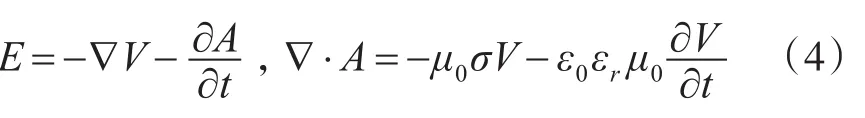
利用式（4），可得

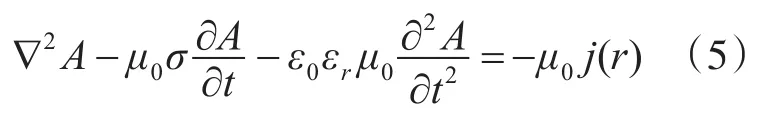
谐变场的复数表达式为B=B0eiwt，E=E0eiwt，A=A0eiwt，把这些关系式带入麦克斯韦方程中，则得电流源频率域麦克斯韦方程为

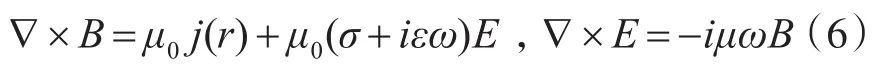
式（6）可以化简为

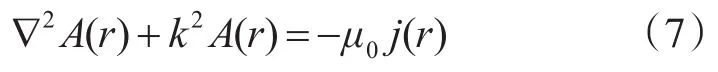
将源在边界条件处进行单独处理，源之外的区域麦克斯韦方程满足齐次赫姆霍兹方程：

2.2 边界条件

水下介质分布在半无限空间中，现在用一个足够大的区域代替半无限空间，需要考虑边界条件，用计算区域人工边界S1上的第一类边界条件来表达源j（r）的作用，即

其中Ap为源在均匀半空间的解，空气及海水中的电导率为σ1和σ2，对于X方向偶极距为I0ds的电场场源，假设电偶极子位于( )x0,y0,z0，对于任意一点，可以得到均匀半空间电磁场位势解的分量形式。

空气层方程的解（z＜0）：

海水中方程的解（z＞0）：

在海水和海床分界面处边界条件满足：

其中，n为垂直分界面的法向分量。

3 仿真计算

3.1 模型建立

本文采用三维模型进行倾斜海床环境三层水下场源电场特性仿真计算，根据图3所示的示意图建立三维模型，如图2所示。

图2 倾斜海床三层仿真模型

该模型为具有有限元域的模型，有限元域的主要作用是对辐射波的吸收。其中内部主要计算域尺寸为100m×100m×200m，有限元域厚度为10m。海水深约为100m，电场场源位于水下70m，偶极矩为10A·m，方向沿X负方向。测线选在海床表面沿X方向中线处。

3.2 材料参数设置

本文需要设置材料的物质是三层介质：空气、海水及海床。具体参数如表1所示。

表1 材料参数

3.3 网格划分

本文基于媒介物质及所研究的区域对模型进行网格划分。为了保证计算结果的收敛性和特性曲线的平滑性，本文对求解域及无限元域进行了网格扫掠，特别对场源附近区域进行了网格的加密处理，网格划分结果如图3所示。

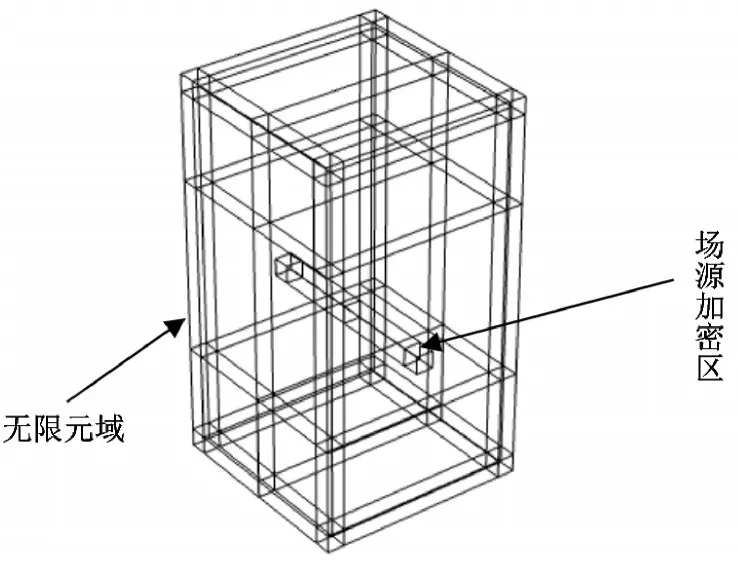
图3 倾斜海床三层模型网格划分

4 仿真结果分析比较

本文采用稳态求解，对比不同海床倾斜角、不同海水电导率及不同海床电导率情况下水下电场源在测线处所产生的电场分布特性。由于场源偶极矩方向为X方向，所以下面列出各情况下测线处总电位、Ex、Ez的分布特性，如下所示。

图4 不同海床倾角情况下总电位、Ex分量及Ez分量对比

5 结语

本文根据媒介电导率的不同将海洋环境分为空气-海水-倾斜海床三层模型，利用COMSOL Multiphysics有限元仿真软件计算得出倾斜海床环境中电偶极子水下电场分布特性，并对比不同海床倾斜角度、不同海水电导率、不同海床电导率下电场分布特性。

经仿真计算对比得到以下结论。

1）随着海床倾角的逐渐增大，水下场源电场总电位、Ex分量、Ez分量分布特性曲线形态基本不变，但幅值随角度的增大有所偏移。

图5 当倾角为5°时不同海水电导率情况下总电位对比

2）当海床倾角一定时，水下场源电场总电位、Ex分量、Ez分量分布特性曲线形态基本不变，幅值随海水电导率的增大而减小。

图6 当倾角为5°时不同海床电导率情况下总电位对比

3）当海床倾角一定时，水下场源电场总电位、Ex分量、Ez分量分布特性曲线形态基本不变；对于Ez分量而言，海床电导率几乎无影响；对于总电位和Ex分量而言，当海床电导率为1S/m时电场特性曲线幅值减小。