基于高阶组合能量算子的滚动轴承故障诊断*

陈霁恒 朱丹宸 谭经松

（海军士官学校 蚌埠 233000）

1 引言

滚动轴承作为旋转机械的关键零部件得到了广泛的使用，然而，由于其常工作在高温、高速和重载等恶劣环境中，导致故障时有发生，极大地影响着整个设备的使用性能和安全运行，因此，开展针对滚动轴承的状态监测和故障诊断就显得尤为重要。而目前，受到测量手段的限制，在结构较为复杂的设备中，滚动轴承和信号测量所用传感器之间常存在较为复杂的传递路径，导致较强的信号能量衰减，致使测得的信号中故障特征微弱，且伴随着强背景噪声，给准确的滚动轴承故障特征提取带来较大的困难。就运行状况来看，滚动轴承常工作在时变转速工况下，导致故障产生的冲击信号失去了周期性特征，故障特征频率随着时间不断变化，信号存在强烈的非平稳特性，此外，许多经典的信号处理方法无法直接应用于变转速工况下的滚动轴承故障特征提取。

近年来，变转速工况下的滚动轴承故障诊断得到了广泛的研究，且取得了不少成果，其中，阶次跟踪作为最常见的方法之一［1～2］，被用于消除转速波动带来的影响。阶次跟踪的核心是通过角域重采样将非平稳的时域信号转换成平稳的角域信号，然而经典的阶次跟踪方法依赖于编码器或者转速计以提供轴承的瞬时转频、相位作为参考，易受到测试条件的限制。因此，许多学者研究利用短时傅立叶变换（Short Time Fourier Transform，STFT）等时频分析方法，提取出信号中的瞬时转频信息，实现了无转速信号的阶次跟踪［3～6］。然而，该方法计算结果的准确性和有效性受到计算过程的制约，如Vold-Kalman滤波常被用于提取时频图中的某一阶瞬时频率，然而，求解过程中包含大型稀疏矩阵求逆，极大地增加了计算的复杂度，降低了计算效率。除此以外，为了避免重采样过程产生的误差，也可以通过提取时频图中瞬时故障特征频率和瞬时转频曲线，利用两者间的瞬时比值确定轴承的故障类型。考虑到轴承故障信号中的强背景噪声干扰，一些常见的信号分析方法也被用于提高信号的信噪比，如 EWT［7］、EMD［8］、AR 模型［9］等，进一步提高了故障特征提取的有效性。

在实际测量过程中，系统中的齿轮啮合，不平衡、不对中故障，转频调制等现象均会导致振动信号中存在明显的转频成分，且不易受高频噪声的干扰；然而，复杂传递路径会导致微弱的故障特征被背景噪声所淹没，不利于瞬时故障特征频率曲线的准确提取。基于此，为了方便实际使用，本文提出了一种无需转速信号的变转速工况下滚动轴承故障特征提取方法，首先，利用STFT和短时Chirplet-Fourier变换对滚动轴承故障信号进行时频表示，为了减小计算误差，提取出时频图中多阶明显的转频分量，通过算术平均的方法得到最终的瞬时转频曲线，并基于此实现时域非平稳信号的角域重采样；为了提高重采样信号的信噪比，提出基于改进高阶组合能量算子的冲击特征增强方法；最后，通过FFT得到的阶次谱实现了滚动轴承故障特征的有效提取。

2 改进高阶组合能量算子的基本原理

2.1 高阶能量算子的原理

高阶能量算子在计算过程中，只需要知道信号的幅值和导数，计算的复杂性较低，效率较高，对信号的瞬态变化较为敏感，能够准确估计信号的瞬时幅值包络和瞬时频率。

对于连续信号x（t），其高阶能量算子表示为［10］

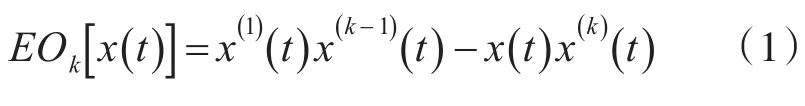
式（1）中，k为能量算子的阶数，x（k-1）和 x（k）分别表示信号的k-1阶和k阶导数。

对于离散时间信号x（n），其高阶能量算子可以表示为［11］

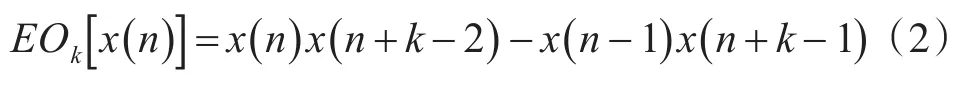
分析式（1）和式（2）可知，当阶数k=2时，高阶能量算子即为最常用的Teager能量算子。相比于Teager能量算子，高阶能量算子进一步增强信号中的瞬态成分，因此，可将高阶能量算子用于提取滚动轴承故障冲击特征。但由于高阶能量算子在计算时使用了差分算子，在增强冲击成分的同时，也会增强信号中的高频噪声成分，由此，选取合适的阶数就显得尤为重要。

2.2 高阶组合能量算子的构造方法

为了充分发挥高阶能量算子的解调能力，最大限度的提取原始振动信号的冲击成分并减小噪声成分的干扰，考虑到2～j阶能量算子的结果中，可能存在噪声干扰较为严重，特征提取效果不佳的分量。基于此，本文提出了一种新的高阶组合高阶能量算子，具体的构造方法如下。

1）确定能量算子的最大阶数K，为了提高计算效率，K值不宜取过大，本文将K设定为20；

2）为了提高分析效果，对2～K阶能量算子进行预先筛选，去除其中冲击特征不明显的阶数，本文提出利用高阶能量谱峭度作为指标。首先，设离散时间信号x（n），其长度范围为1～N，采样频率为fs，对第k阶能量算子进行快速傅里叶变换得：

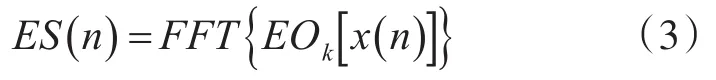
式（3）中，ES（n）表示频率范围为0～fs/2范围内的高阶能量谱值。其次，峭度可以衡量信号中明显的峰值和冲击成分，假设ES（n）的均值为μES，则高阶能量谱峭度可以定义为

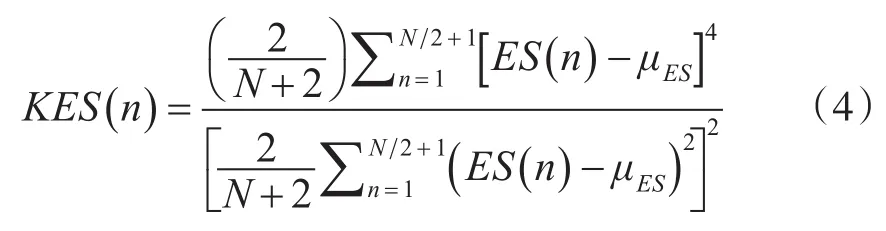
对于高阶能量谱来说，如果高阶能量算子的结果中包含明显的故障冲击成分，则在能量谱中，故障特征频率处表现为明显的峰值，会导致峭度值的增加，因此，以高阶能量谱峭度为指标可以选取出高阶能量算子中故障特征较为明显的阶数，本文将选取的数量设定为6；

3）假设选取出的6阶能量算子的阶数分别为k1、k2、k3、k4、k5和 k6，则信号 x（n）的高阶组合能量算子可以表示为

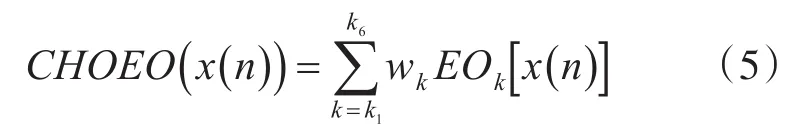
式（5）中，wk表示第k阶能量算子对应的加权系数，本文设定其取值范围确定为0～1。

2.3 加权系数的优化选取策略

从式（5）可以看出，需要对加权系数wk进行优化选取以保证高阶组合能量算子的分析结果。粒子群算法（PSO）作为一种常见的优化算法由于其较好的寻优能力得到了广泛使用。假设PSO的种群数量为N，搜索空间的维度为D，则对于空间中的任意一个粒子i，其位置和速度向量可分别表示为为粒子 i的最佳位置可以利用一个向量进行表示，Pbest=，整个种群的最佳位置可以表示为粒子i的位置和速度需要进行随机初始化，且按照一定公式的进行调整更新：

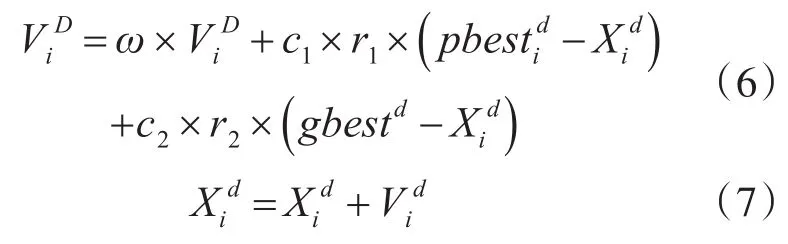
由于在经典的粒子群优化中，寻优过程缺乏多样性，导致搜索结果容易出现局部最优解，并提前收敛。为了解决这些问题，本文选取了一种改进的粒子群算法［12］。

由于信息熵可以衡量信号中的不确定度，表征信号中随机噪声的含量，对于轴承故障信号而言，越小的信息熵值表示信号中的随机噪声干扰越小，故障特征越明显，因此，本文将熵作为优化过程中的适应度值，且最小熵所对应的粒子位置即是所需的最优解。对于离散时间信号x（n），假设其fourier变换结果为X（ω），则其能量谱可以定义为

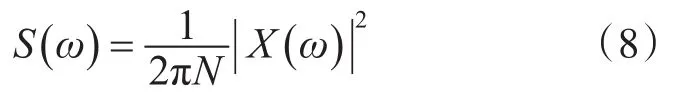
那么，归一化的信息熵可以定义为［13］

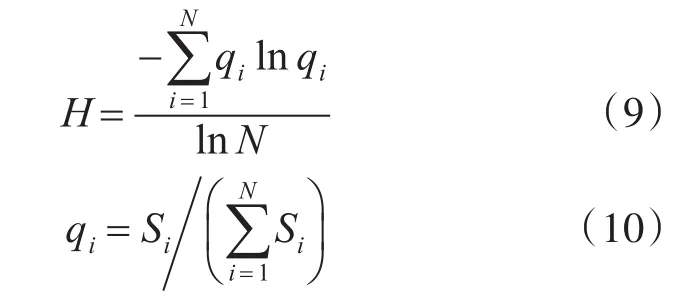
式（10）中，Si表示能量谱中的第i个值。

3 瞬时转速估计方法

短时Chirp-Fourier变换作为一种类似于STFT的时频表示方法，具有时频聚焦特性，可以使分析得到的时频图中瞬时转频的脊线更加清晰，其数学表达式为［3］

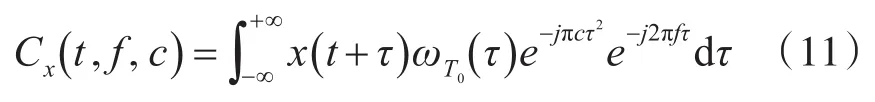
式（11）中，ωT0表示中心时刻为τ=0长度为T0的窗。短时Chirp-Fourier变换不再受到信号需要局部平稳的条件限制，而是通过中心频率为fτ，调制频率为c的基函数对任意时刻信号的时频特征进行匹配，从而实现信号的分段逼近，STFT是c=0的特殊情况。

由此，更为清晰的瞬时转频曲线可通过在局部范围内取最大值的方式获得［14］：

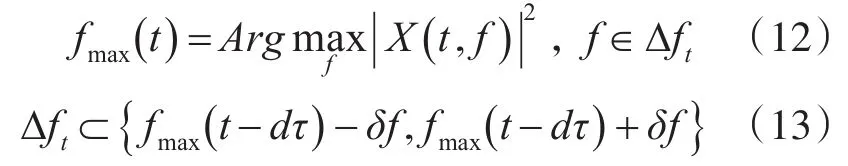
由此，本文提取瞬时转速的过程可以总结为如下。

1）基于STFT、式（12）和（13）对转频进行初步估计，选取了N个明显的谐波分量，记为Fkn(t)；

2）依据中心差分法，分别对各阶谐波分量的瞬时调频值进行计算［3］：

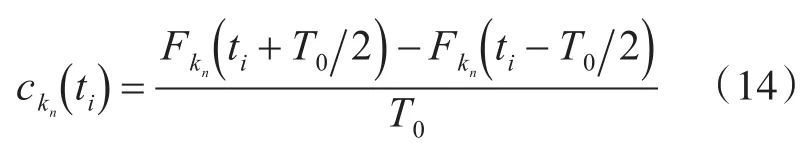
3）式（14）中，ti为第i个窗的中心时刻，ckn(ti)表示第i个窗内第kn阶谐波分量的调频估计值；

4）将ckn(ti)带入式（11），对原始信号进行短时Chirp-Fourier变换，分别得到N个脊线更为清晰的时频表示图；

5）提取出第kn阶谐波表示的瞬时频率值，记为fkn(t)，则最终提取得到的瞬时转频为

问卷调查尽量以随机抽样为主，所以调查时采用简单随机抽样来计算大学生群体的样本量，其计算公式为，其中：为总体总量；为一定置信水平下对应的标准正态临界值；为抽样概率；为抽样极限误差.

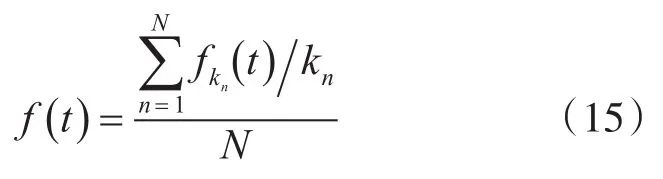
4 故障特征提取流程

本文考虑到滚动轴承工作在变转速工况下的特点，结合强背景噪声干扰的实际，提出基于改进高阶组合能量算子的变转速工况下滚动轴承弱故障特征提取方法。算法的流程如图1所示，具体过程如下。

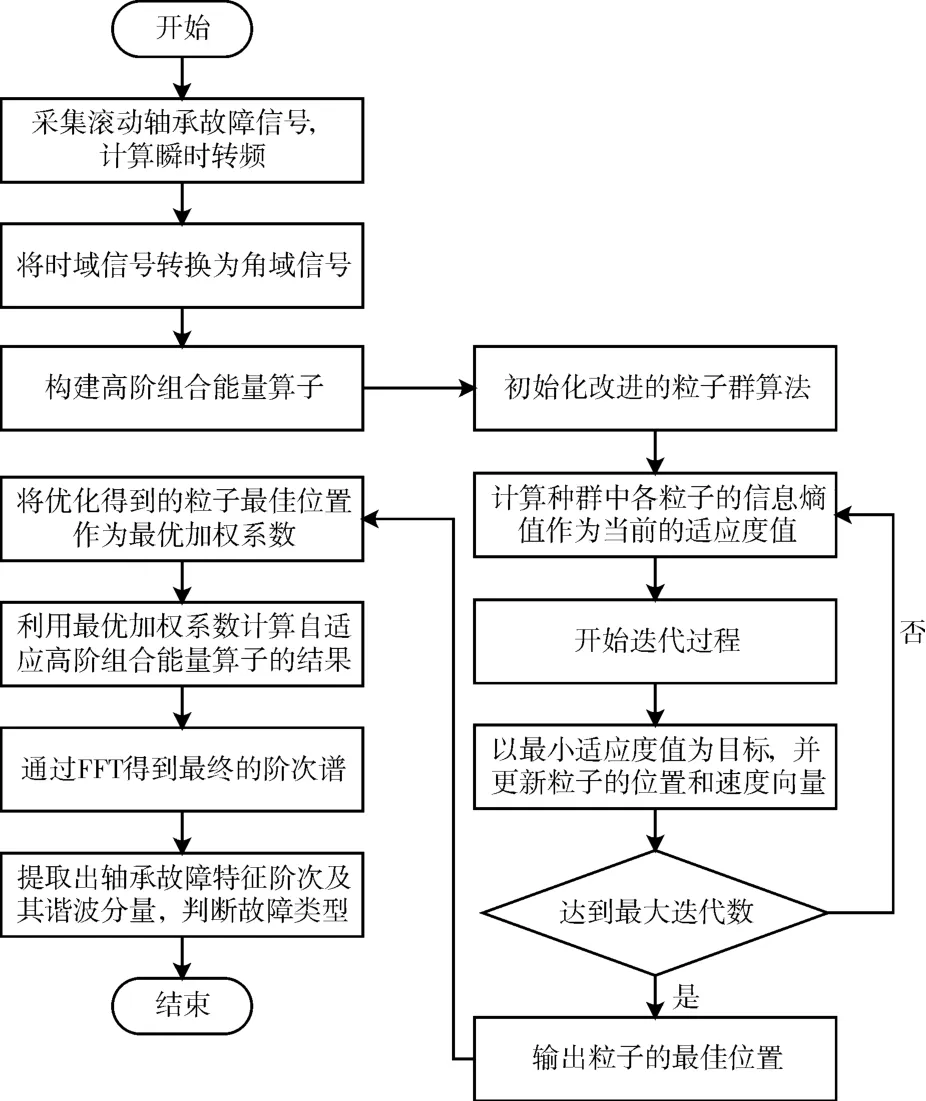
图1 本文算法流程

1）采集滚动轴承在变转速工况下的振动信号，基于短时Chirp-Fourier变换计算瞬时转频曲线；

2）基于步骤1）得到的转频曲线，将时域信号转换成角域信号；

3）基于角域信号，构造高阶组合能量算子，利用改进的粒子群算法对加权系数进行优化选取并得到改进组合高阶能量算子的结果；

4）利用FFT处理步骤4）的结果，获得最终的阶次谱。

5）在变转速工况下，需要通过提取故障特征阶次来判断滚动轴承故障类型。滚动轴承内圈、外圈故障特征阶次Oi和Oo可分别表示为

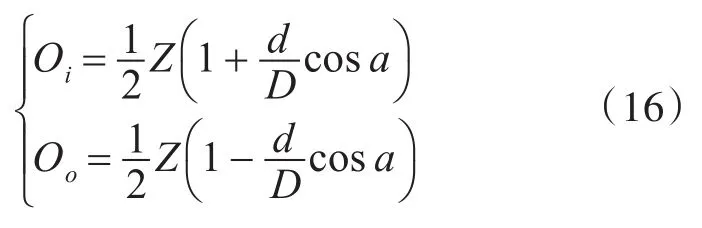
式（16）中，d为滚动体的直径，D为节径，Z为滚动体的个数，α为接触角。由此，通过观察步骤5）得到的阶次谱中幅值对应的阶次，并与理论故障特征阶次相比较，就可以判断滚动轴承故障类型。

5 仿真信号分析

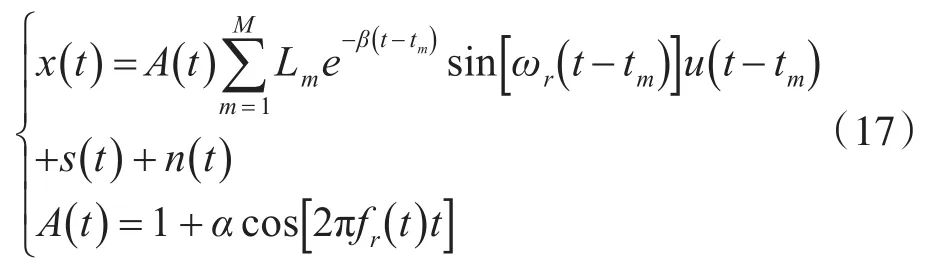
式（17）中，A（t）表示与转频fr（t）相关的幅值调制，α＞0为一个常数；u（t-tm）表示阶跃函数，当t＞tm时，u=1，当t＜tm时，u=0；Lm=L0+ηfr（tm）表示与fr（t）相关的幅值，L0和η均为常数，tm为第m个故障冲击的时间；s（t）和n（t）分别表示信号 x（t）中的正弦谐波分量和噪声干扰成分。每个故障冲击的时间tm可以通过下式进行计算［15］：

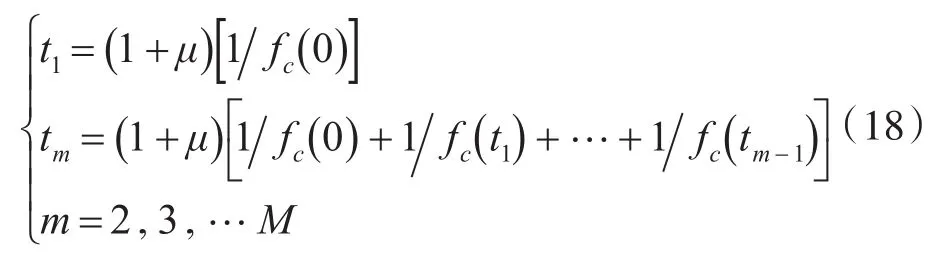
式（18）中，μ表示滚动体的滑移率，fc（t）表示瞬时故障特征频率。谐波分量s（t）可以表示为

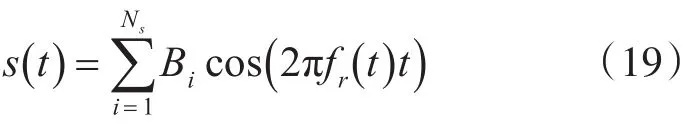
式（19）中，Ns为谐波数量，Bi为第i个谐波成分的幅值。仿真信号的具体参数见表1。将随机噪声的大小确定为-10db，假设fc（t）=5.5fr（t），即故障特征阶次为5.5。仿真信号的采样频率为20000Hz，仿真时长为2.5s。

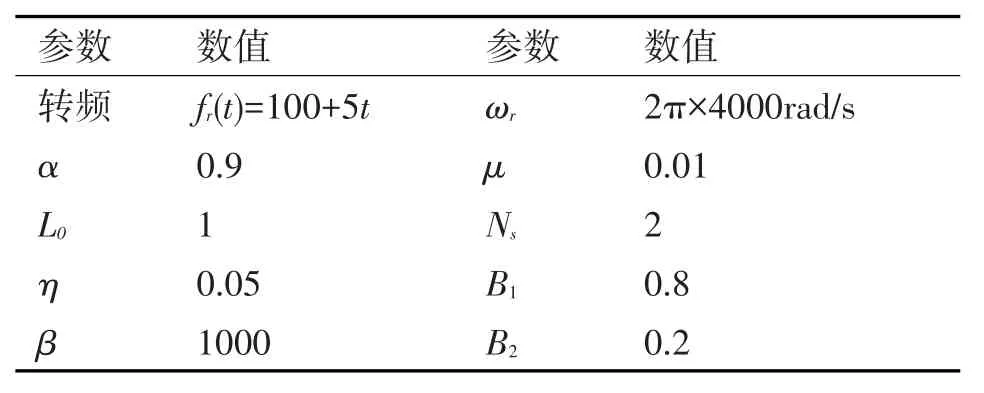
表1 仿真信号参数

利用本文提出的算法分析该仿真信号，首先，基于短时Chirp-Fourier变换对原始仿真信号进行时频表示，结果如图2（a）所示，图中仅能识别出一阶转频曲线，所以瞬时转速计算过程中仅利用该阶分量。提取得到的瞬时转速如图2（b）所示，图中蓝色实线表示计算得到的瞬时转频，红色实线表示理论上的真实转频，通过对比可知，两者之间的差距较小，说明对于该仿真模型，瞬时转频分量得到了有效提取。

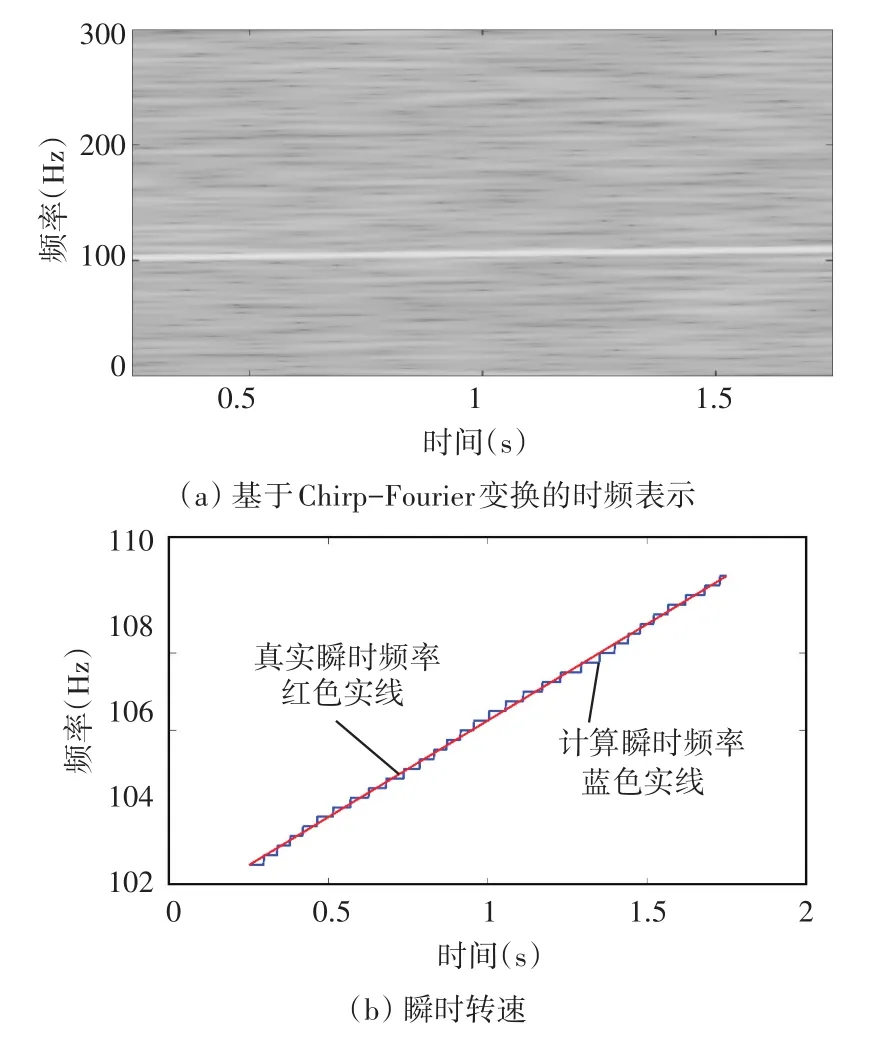
图2 瞬时转速计算

接下来，以计算得到的瞬时转速为基础，通过三次样条插值，对原始仿真信号进行角域重采样，原始时域信号和重采样得到的角域信号分别如图3（a）和（b）所示。

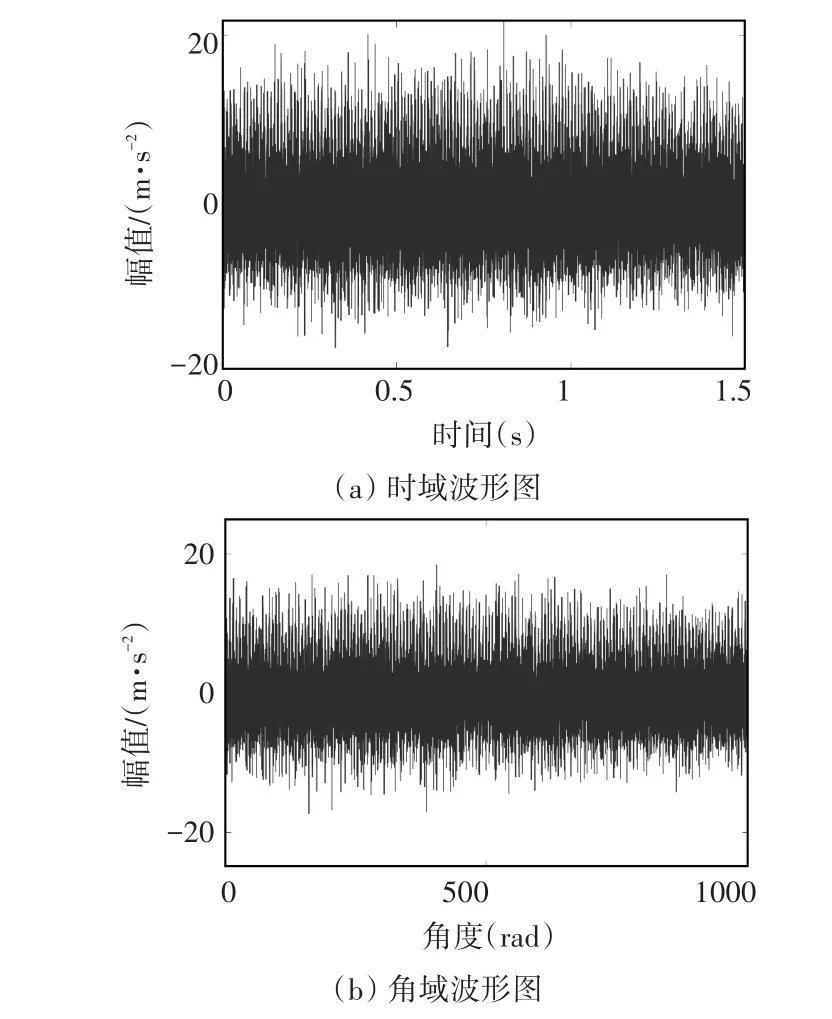
图3 仿真信号的波形图

利用2～20阶能量算子处理图2（b）所示的角域信号，通过比较各阶能量算子的能量谱峭度值，选取第7、5、2、17、12、10阶能量算子（以能量谱峭度值从大到小进行排序）构造改进高阶组合高阶能量算子，使用优化算法时的种群个数和最大迭代数分别设定为100和300，结果如图4所示。图4（a）为优化时的收敛曲线，从图中能够看出，当迭代次数为222时，适应度函数取到最小值0.6238，此时对应的粒子位置为［0.5115，0.0112，0.9903，0.4436，0.3986，0.0236］，将此时的粒子位置作为高阶组合能量算子的最优加权系数，得到的最优组合能量算子结果如图4（b）所示，通过FFT可以得到最终的阶次谱如图4（c）所示，图中展示的最大阶数为30。阶次谱中1阶及2阶转频较为明显，在阶次5.45（与理论值故障特征阶次5.5接近，滑移率的存在导致了两者间的误差）及其谐波成分10.9和16.35处出现明显的峰值，围绕故障特征阶次及其谐波成分，间隔为转频的调制边频带也能够得到识别，以上特征符合仿真模型的设置，可以判断该滚动轴承存在内圈故障。

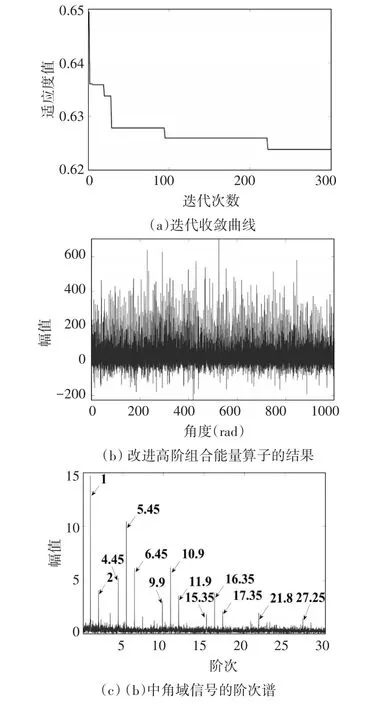
图4 本文算法处理仿真信号的结果

作为对比，本文利用EMD［8］处理图3（b）所示角域信号，分别计算分解得到的14个IMF的峭度值及其与原始信号的相关系数ρ，作为选取有效IMF的依据。将有效分量ρ的阈值设定为0.1。图5（a）展示了分解得到的前4阶IMF，通过计算，第1、2、3、4、5和7阶IMF的相关系数大于0.1，值分别为0.77、0.46、0.24、0.17、0.14、0.18，这6阶IMF的峭度值分别为 3.26、3.08、2.84、2.81、2.93、2.32。由于IMF1的峭度值最大，所以对IMF1进行包络分析，结果如图5（b）所示。包络谱中仅能明显识别出转频成分，故障特征阶次5.45及其调制边频带，且各特征的幅值明显小于图4（c）中的幅值，通过比较，本文提出的方法可以在噪声的干扰下，提取出更为丰富和明显的故障信息，体现出方法的有效性。

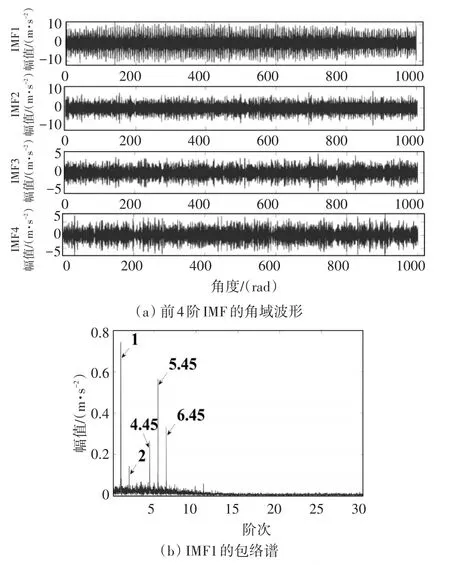
图5 EMD方法处理角域信号的结果

6 实验数据验证

本节使用试验台测得的滚动轴承故障信号进行进一步分析，试验台的具体结构如图6所示。实验过程中将测点选在靠近支撑结构的基座上，测量垂直于台面方向的振动。由于测点远离故障点，复杂的传递路径使实测信号包含了更多的干扰成分，增大了故障特征提取的难度。为了模拟滚动轴承在变转速工况下运行，实验时的平均转速为3000r/min并以300r/min上下做正弦波动，受到转速波动的影响，进一步加大了实测振动信号的复杂性，增大了故障特征提取的难度。

图6 试验台

实验所用轴承为NSK7010c，其结构参数见表2，信号采集时的采样频率设定为32768Hz，采集时长为2s，通过计算可知该轴承的外圈故障特征阶次为8.27。实测信号的时域波形如图7（a）所示，受到转速波动以及背景噪声的干扰，时域图中无法识别轴承故障导致的冲击成分。理论上，轴承外圈故障信号中不应该包含转频信息，然而，由于该故障模拟平台同时存在不平衡故障，导致采集得到的振动信号中包含转频信息，由此，依旧可以使用本文提出的算法分析实测信号。

表2 测试轴承参数

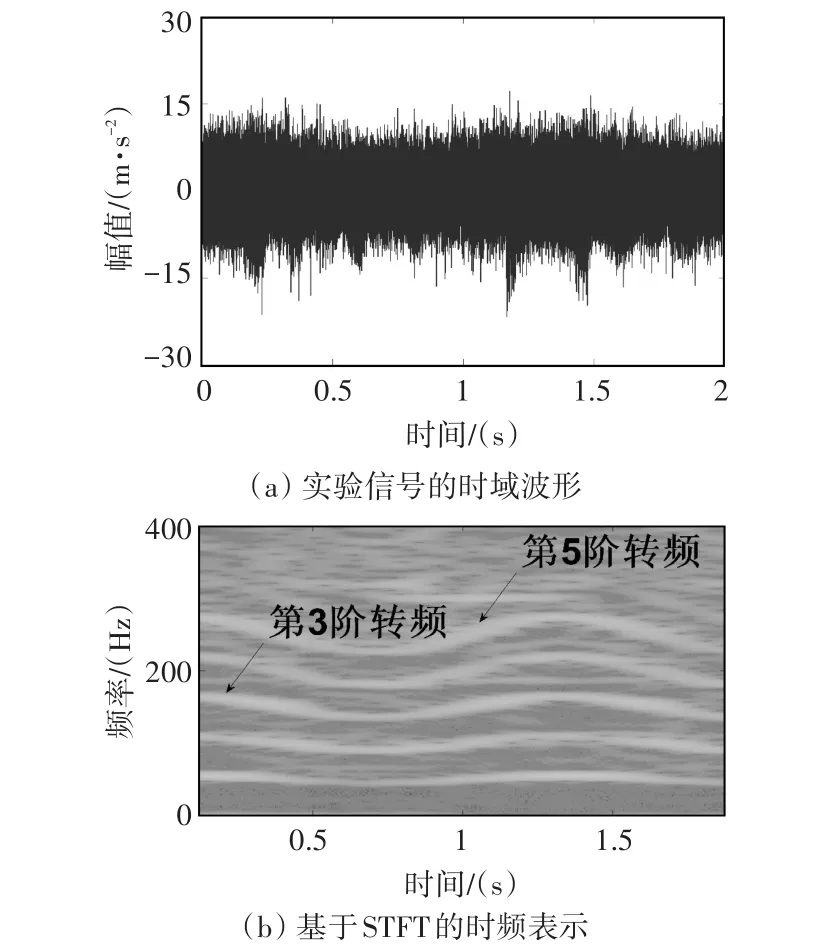
图7 实验信号及其时频表示

图7（b）为利用STFT分析原始振动信号的结果，时频图中可以识别出1至5阶转频分量，通过计算可知，利用时频图中第3阶和第5阶转频曲线，可以有效提取瞬时转频，结果如图8所示。图8（a）为提取第3阶转频成分时，通过短时Chirp-Fourier变换得到的时频图，对比图7（b）中的第3阶转频，图8（a）中的第3阶转频曲线更为明显和聚集，有利于转频的提取，提取结果如图8（b）所示。同理，图8（c）为提取第5阶转频成分的时频图，提取得到的瞬时转频如图8（d）所示。

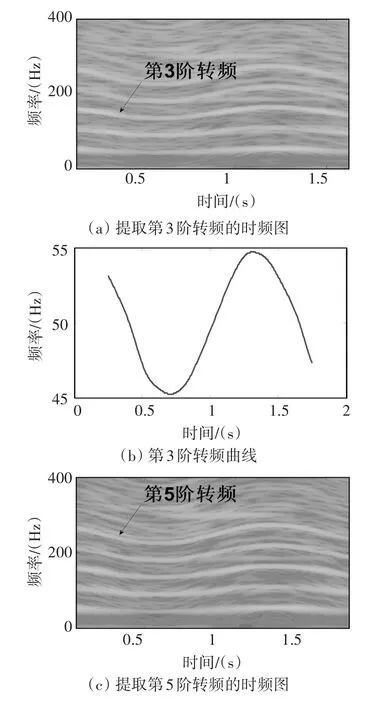
图8 瞬时转速计算结果

为了减小随机误差，对提取得到的两阶转频曲线进行平均，图9的平均转频曲线大致在45Hz和55Hz之间做正弦波动，这与设定的转频波动方式是一致的。下面利用该平均转频曲线进行角域重采样，得到的结果如图10（a）所示。通过计算2～20阶能量算子的能量谱峭度值，选取17、15、19、14、4和16阶能量算子构造高阶组合能量算子进行后续分析。

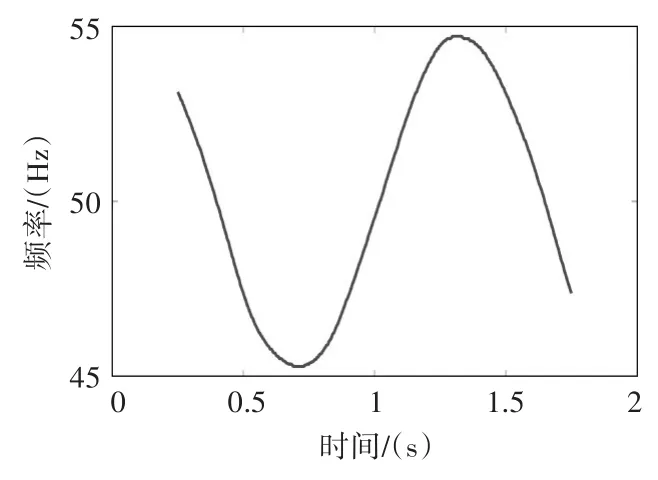
图9 3阶和5阶转频曲线的平均值

通过优化算法对构造的高阶能量算子的加权系数进行优化选取，优化过程的收敛曲线如图10（b）所示。根据收敛曲线，当迭代次数为117次时，可以取到最小适应度值0.7911，此时对应的粒子位置为［0.053，0.539，0.867，0.668，0.353，0.001］，将该粒子位置作为最优加权系数进行高阶组合能量算子的计算，结果如图10（c），利用FFT分析该高阶组合能量算子，最终的阶次谱如图10（d）所示，图中阶次为8.3处的谱线幅值较为突出（与外圈故障特征阶次的理论值相接近），同时其2～6阶谐波成分阶处的幅值也较为明显，背景噪声虽然存在但干扰较小，滚动轴承的外圈故障特征得到了准确提取，证明了本文提出方法的有效性。

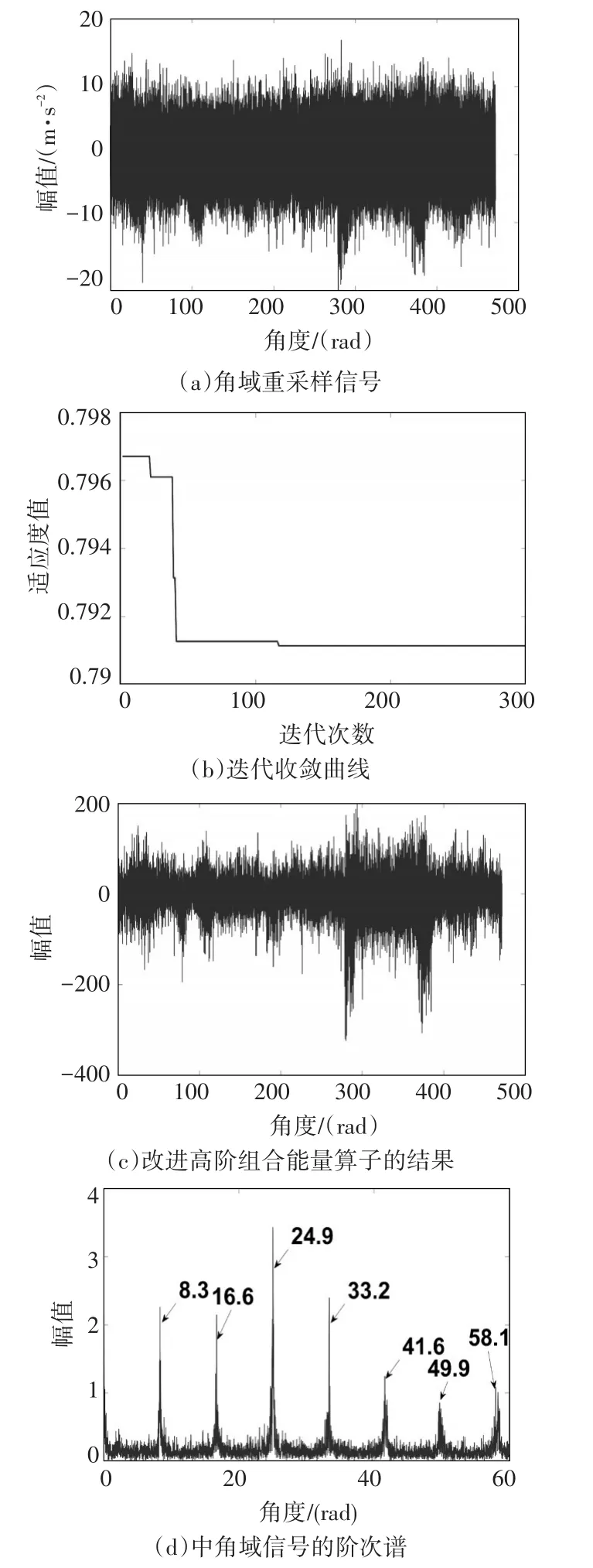
图10 本文算法分析实验信号的结果

与仿真分析类似，利用EMD处理重采样得到的角域信号，减小噪声的干扰，提取故障特征成分，结果如图11所示。EMD分解共得到了16个IMF，图11（a）展示了其中的前4阶，分别计算各阶IMF与原始信号的相关系数，仅有前4阶IMF的ρ＞0.1，分别为0.783、0.526、0.291和0.134。前4阶IMF的峭度值分别为2.446、2.641、2.73和2.851，选取峭度值最大的IMF4进行包络分析，得到的包络谱如图11（b）。包络谱中仅有8.3阶处的幅值较为突出，与外圈故障特征阶次相对应，然而其谐波成分未得到有效提取，分析效果欠佳。通过对比，进一步验证了本文算法在变转速工况下，从强背景噪声干扰中提取弱故障冲击特征的能力。

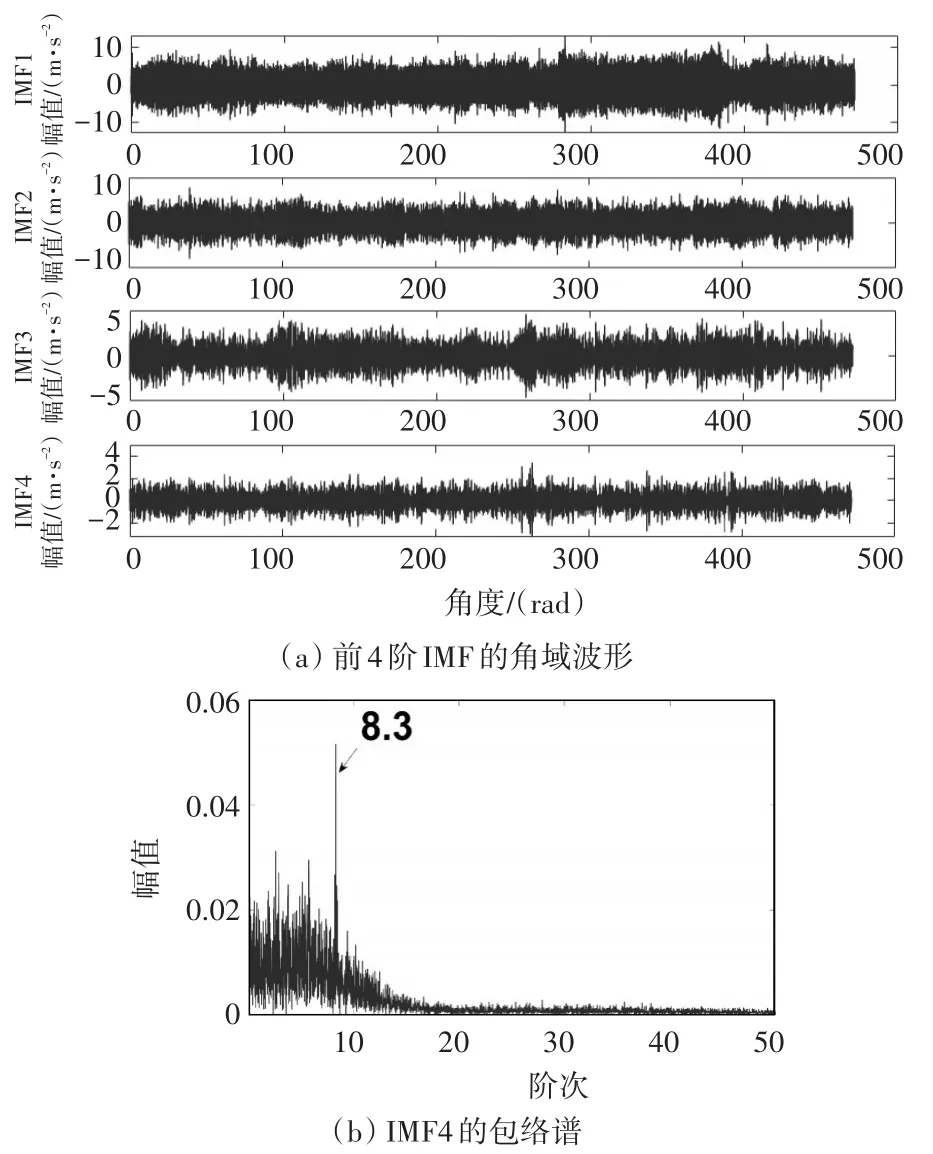
图11 EMD分析实验信号的结果

7 结语

滚动轴承在实际工作过程中常处于转速波动或是升、降速的工况下，从而导致许多经典的故障诊断方法失效，结合复杂传递路径影响下，故障产生的冲击成分较为微弱常被背景噪声所淹没的特点，提出基于改进高阶组合能量算子的变转速工况下滚动轴承弱故障特征提取方法，本文的研究结果表明。

1）利用原始振动信号的时频图进行瞬时频率的估计，并基于此实现时域信号的角域重采样，可以消除转速波动的影响，避免了对于转速信号的依赖，计算过程较为简便，具有良好的适用性。

2）基于高阶能量算子能够增强信号中冲击成分的特点，提出了改进高阶组合能量算子的构造方法，并将其运用于增强滚动轴承的故障特征，能够实现比单一阶数能量算子更好的效果；

3）仿真和实测信号的分析结果表明，本文提出的方法能够在转速波动和强背景噪声的影响下，准确提取出滚动轴承故障特征，且与基于EMD的包络阶次方法相比，本文方法提取出的故障信号更为丰富，诊断效果更佳，具有更强的工程实践应用价值。