柔性边界三轴压缩条件下胶结型水合物沉积物力学特性的离散元模拟

周世琛，霍文星，周博，薛世峰

(中国石油大学(华东) 储运与建筑工程学院，山东青岛，266580)

水合物沉积物是一种由天然气、水合物、砂土和气相等组成的特殊的混合颗粒材料。天然气水合物资源具有储量大、能量密度高和燃烧清洁等优点[1]，被公认为是一种极具开采潜能的能源。日本和中国开展了海域天然气水合物资源的试采作业[2]。勘探与开采会影响天然气水合物沉积层所处的地质环境，甚至可能破坏水合物赖以稳定存在的相平衡条件，进而引起水合物的分解，并可能带来一系列的工程地质灾害[3-4]。因此，全面深入地研究天然气水合物沉积物的力学特性对于其安全开采具有重要的意义。

针对天然气水合物沉积物的力学特性，国内外学者开展了卓有成效的试验研究[5-7]，部分学者基于连续介质理论提出了宏观本构模型[8-10]。试验和连续介质理论方法多关注于宏观尺度方面，重点研究了水合物的赋存模式、含量及其边界条件等对天然气水合物沉积物强度和变形特性的影响。而作为一种颗粒材料，天然气水合物沉积物在宏观尺度上表现出类似于连续介质的力学特性，而在微细观尺度上具有非连续和非均匀的基本特性，形成了“颗粒(微观尺度)-力链(细观尺度)-体系(宏观尺度)”的多尺度结构[11]。随着离散元法[12](DEM)的发展，微细观力学机理的研究已经成为颗粒材料研究的热点话题。

近年来已有不少学者采用离散法研究了天然气水合物沉积物的力学特性。BRUGADA等[13]模拟了孔隙填充型水合物沉积物的宏观力学行为，并讨论了水合物含量、围压等因素对强度和变形参数的影响；JIANG等[14-15]提出了微观胶结模型，考虑了不同的水合物赋存模式，研究了水合物含量、温度和应力路径等因素对水合物沉积物宏观力学特性的影响。JUNG等[16]对水合物呈分散和颗粒簇形式的天然气水合物沉积物的力学行为进行了模拟，分析了初始孔隙率、水合物含量等对刚度、强度和剪胀性等特性的影响。JIANG等[17]分析了水合物的含量、加载速率对胶结型水合物沉积物的强度和变形特性的影响，并讨论了力链、孔隙率以及颗粒转动角的演化过程。WANG 等[18]研究了胶结型水合物沉积物在循环荷载条件下的宏观力学特性，并重点分析了细观组构特性的演化特征。周博等[19]针对孔隙填充型水合物沉积物，重点研究了主应力系数对宏观力学行为和组构各向异性的影响。周世琛等[20-21]研究了胶结型水合物沉积物在不排水和排水条件下的多尺度力学特性。DING等[22]研究了水合物赋存状态对水合物沉积物的应力-应变-剪胀特性的影响，并解释了水合物影响峰值强度和割线模量的微细观力学机理。

在上述研究中，水合物沉积物离散元试样的侧向边界均采用刚性边界，而室内三轴试验的侧向边界是柔性橡胶膜。橡胶膜不仅能够施加和维持一定的目标围压，而且允许试样发生自由变形。橡胶膜的弹性行为对试样的强度特性和变形破坏形式有较大影响。此外，对于水合物是如何影响天然气水合物沉积物的宏观力学特性仍然缺乏微细观尺度的解释。

基于此，采用离散元法并引入Wall-Zone 耦合方法模拟侧向柔性边界，对不同水合物饱和度的胶结型天然气水合物沉积物试样进行了离散元三轴数值试验，从宏观角度研究了试样的强度和变形特征，并从微细观角度探究了水合物在对外部荷载的响应中的作用。

1 离散元数值试验

1.1 试样制备

水合物沉积物的骨架由砂土和水合物2种固相组成。对于三维情况，这2种材料均采用球形颗粒单元来模拟。图1所示为胶结型水合物沉积物离散元模型的主要创建流程，创建模型的详细步骤如下：

1)根据Toyoura砂的颗粒粒径级配生成初始孔隙率为0.40的砂土骨架(见图1(a))；

2)根据水合物的饱和度及其粒径计算出水合物颗粒数量，在墙体内部随机生成特定数量的水合物颗粒，然后将所有接触赋予线性接触模型并平衡模型(见图1(b))；

3)给所有的水合物颗粒施加随机方向的力(图1(c))，同时固定砂土颗粒的位置，绝大水合物颗粒会运动至砂土颗粒接触处并在达到平衡状态后逐步累积，部分水合物颗粒运动至砂土颗粒与墙体边界接触处达到平衡状态，如图1(d)所示；

4)将配位数少于3的水合物颗粒判定为悬浮颗粒(实际上这些悬浮的水合物颗粒几乎全部位于墙体边界位置)，给它们施加朝向模型几何中心的力(图1(e))，同时固定其他颗粒的位置，大部分悬浮的水合物颗粒将运动至砂土颗粒接触处并达到平衡状态，如图1(f)所示；

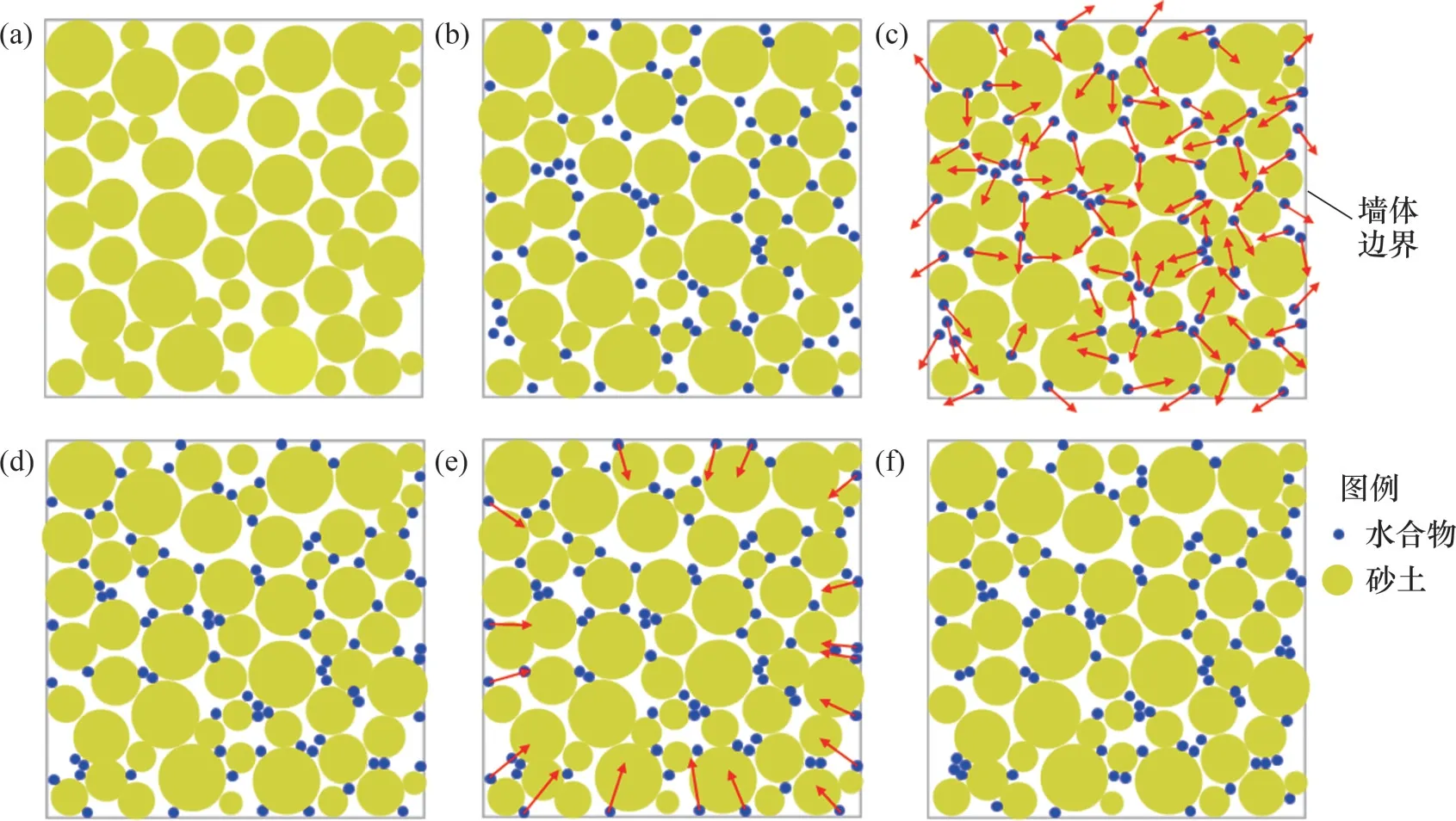
图1 胶结型水合物沉积物离散元模型主要创建流程Fig.1 Main process of generating DEM model of cementing type GHBS

5)统计剩余的悬浮的水合物颗粒数目，如果该数目占水合物颗粒总数量的比例小于1%，那么完成初始模型的创建，否则，将剩余的悬浮的水合物颗粒施加其他方向的力，重复步骤4)和5)；

6)给不同接触设置合适的接触模型并赋值接触模型参数，然后施加目标围压。

水合物沉积物圆柱体模型的直径为5 mm，高度为10 mm。其中，砂土颗粒粒径范围为0.10～0.40 mm，中值粒径约为0.23 mm，密度为2 650 kg/m3，水合物颗粒则采用单一小粒径，粒径为0.06 mm，密度为925 kg/m3。试样的上下边界采用刚性墙作为加载板，而侧面边界采用柔性边界。利用颗粒流软件PFC3D 与有限差分软件FLAC3D实现Wall-Zone界面耦合生成侧面柔性边界(具体原理将在1.2节中介绍)。其中，FLAC3D中壳单元的弹性模量为1.0 MPa，单元厚度为0.05 mm，密度为930 kg/m3。根据初始孔隙率和水合物饱和度确定孔隙中水合物的体积，并计算出试样中水合物颗粒的数量，由此生成了水合物饱和度分别为26%，40%和55%的试样。图2所示为不同水合物饱和度的水合物沉积物试样。

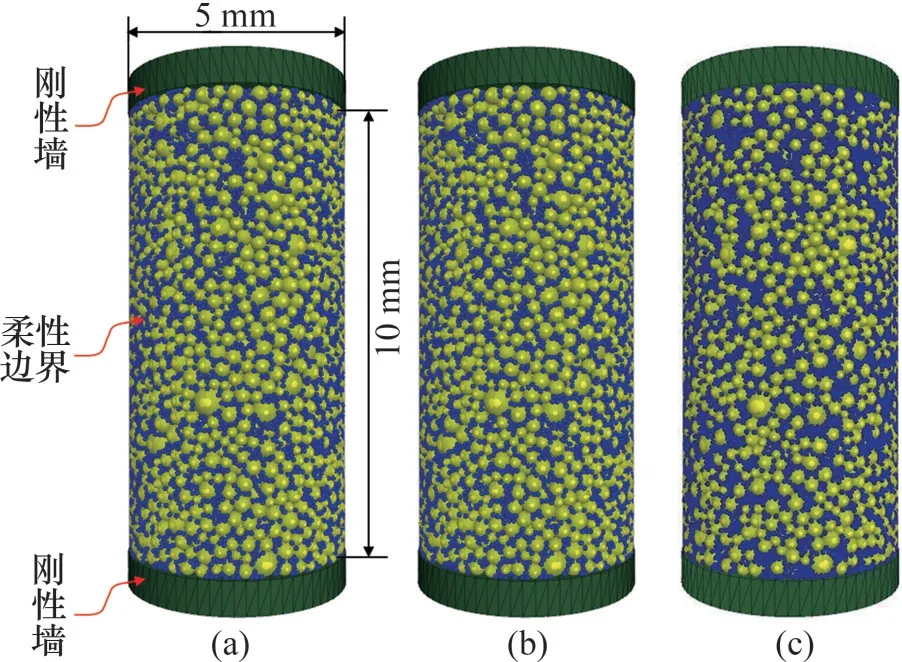
图2 不同水合物饱和度的水合物沉积物离散元模型Fig.2 DEM specimens of gas hydrate bearing sediment with different hydrate saturations

1.2 柔性边界

在标准三轴物理试验中，试样的侧面用橡胶膜包裹以承受围压，底面和顶面采用刚性加载板来实现外力加载。在离散元数值试验中，墙体提供刚性边界，可以模拟上下的刚性加载板，而无法模拟橡胶膜的弹性变形行为，这会限制试样的侧向变形，从而不能有效模拟试样的非均匀局部化变形行为。FLAC3D 中的壳单元可以实现大变形，因此，采用PFC3D和FLAC3D实现Wall-Zone界面耦合以此创建侧向柔性边界。

Wall-Zone界面耦合的原理[23]概述如下：

1)同时创建FLAC壳单元结构与PFC墙体；

2)颗粒与墙体单元作用产生的接触力和力矩根据力系等效定理等效到墙体单元顶点位置，这些墙体顶点上的等效力转移到壳单元节点位置并参与壳单元的运动计算；

3)壳单元节点新的位置和速度传递给墙体单元顶点。

图3所示为Wall-Zone 耦合方法。由图3可见：墙体由三角形单元组成，壳单元结构由三角形单元组成，墙体单元顶点与壳单元节点一一对应(比如墙体单元顶点x1，x2和x3分别对应于壳单元节点x′1，x′2和x′3)。假定某个颗粒与墙体单元x1，x2和x3接触于点P，在墙体单元上与点P最近的点为Q。

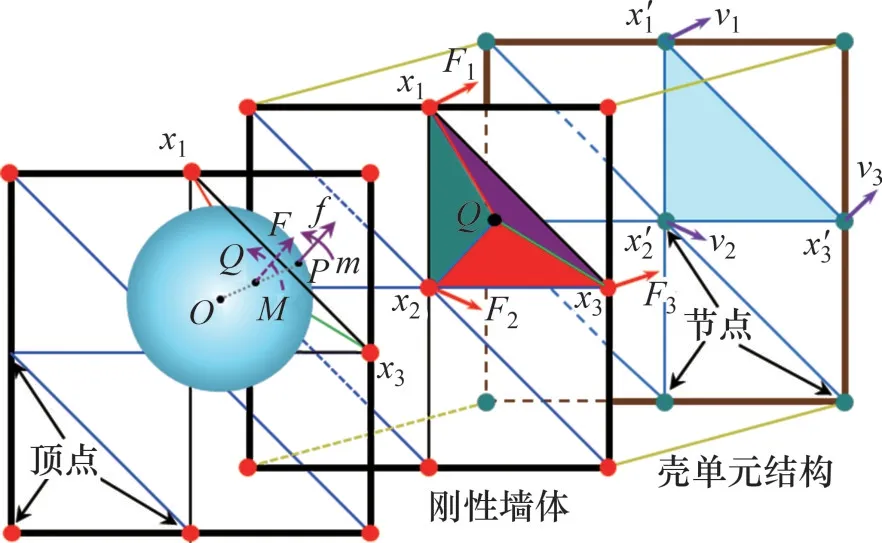
图3 Wall-Zone耦合方法Fig.3 Wall-Zone coupling scheme

首先，将接触点P处的力f和力矩m在点Q处等效为力F和力矩M，并将点Q处的力F和力矩M采用静力等效原则分配到墙体单元顶点x1，x2和x3处，由此得到墙体单元顶点处的力Fi(i=1，2，3)；

其次，墙体单元顶点处的力Fi(i=1，2，3)传递到对应的壳单元的节点x′1，x′2和x′3处；

然后，壳单元根据节点处的力和力矩得到节点的新位置和速度vi(i=1，2，3)；

最后，壳单元节点的新位置和速度传递给墙体单元顶点。

由此完成墙体单元顶点与壳单元节点之间的信息传递。

1.3 接触模型

在离散元法中，接触模型是颗粒之间相互作用的物理准则，它决定了整个颗粒介质的宏细观力学特性。根据邻接单元属性，将水合物沉积物试样内部分为4 种接触类型，包括砂土-砂土、砂土-水合物、水合物-水合物以及颗粒-墙体接触，这4种接触需要选取合适的接触模型来描述单元间的相互作用。YONEDA 等[24-25]发现水合物对相邻的颗粒具有胶结效应。基于这种考虑，将水合物-砂土和水合物-水合物接触赋予线性平行胶结接触模型，而砂土-砂土和颗粒-墙体接触赋予线性接触模型。

因为线性平行胶结模型[26]中包含了线性模型，所以仅对线性平行胶结模型进行概述。图4所示为线性平行胶结接触模型。由图4(a)可知：假设颗粒x(1)的速度和角速度分别是v(1)和ω(1)，颗粒x(2)的速度和角速度分别是v(2)和ω(2)，某一瞬时2个颗粒在C点接触并通过线性平行胶结模型胶结在一起，胶结具有一定的半径和厚度，它既能传递力，又能传递力矩。线性平行胶结模型由平行作用的线性部分和胶结部分组成。其中，线性部分与线性接触模型相同，线性部分的元件由刚度分别为kn和ks的法向弹簧和切向弹簧、摩擦因数为μ的滑动元件、阻尼系数分别为βn和βs的法向阻尼器和切向阻尼器以及标识颗粒间重叠量gs的承压元件组成，如图4(b)所示；胶结部分由刚度分别为k*n和k*s的法向弹簧和切向弹簧、拉伸强度为σ*c的抗拉元件、黏聚力和摩擦角分别为c*和φ*的抗剪元件组成，如图4(c)所示。

在接触点C处设定一个局部笛卡尔坐标系(n，s，t)，其中n平行于接触法向，s和t相互垂直并与n满足右手定则，如图4(d)所示。在该坐标系中，线性平行胶结模型的接触力Fc可以分解为法向接触力Fn和切向接触力Fs，如图4(e)所示。类似地，胶结力矩M*可以分解为胶结扭矩M*t和胶结弯矩Mb*，如图4(f)所示。接触力Fc与胶结力矩M*的计算公式为

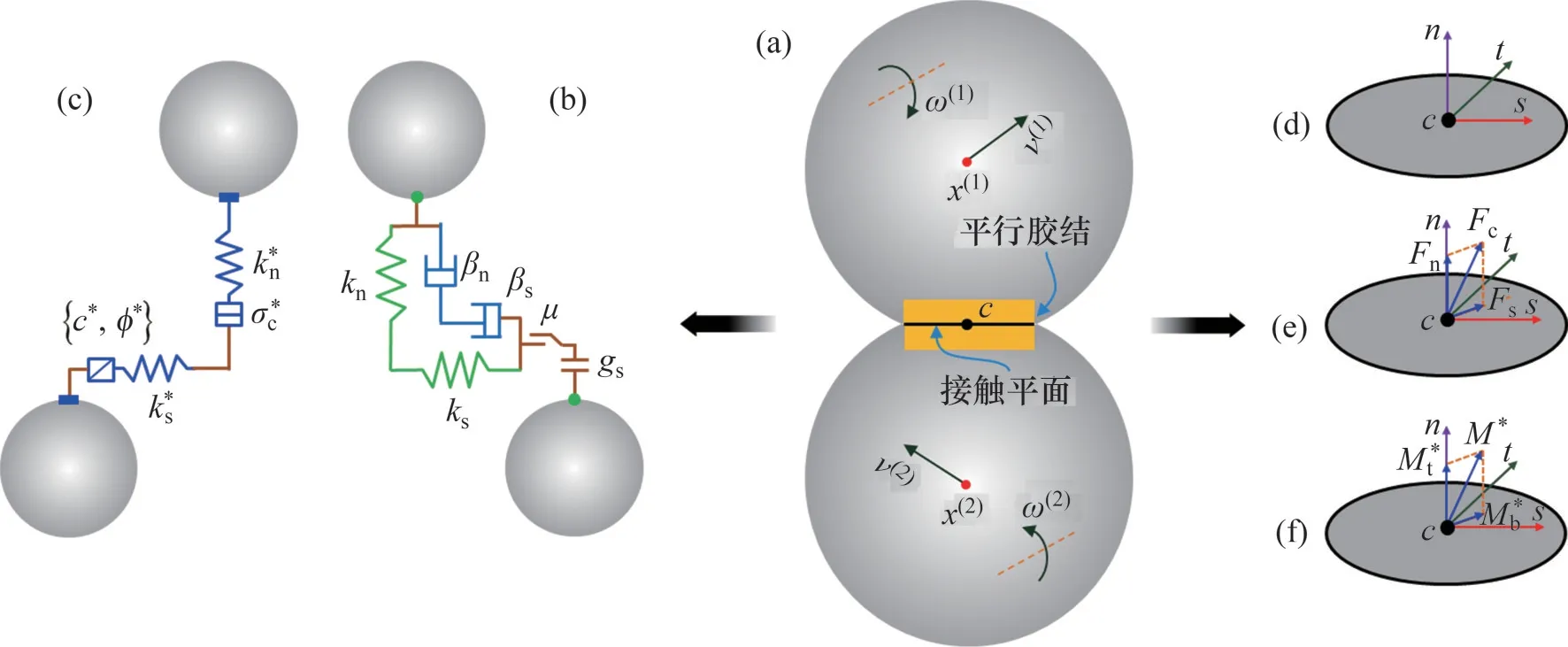
图4 线性平行胶结接触模型[27]Fig.4 Linear parallel bond contact model[27]

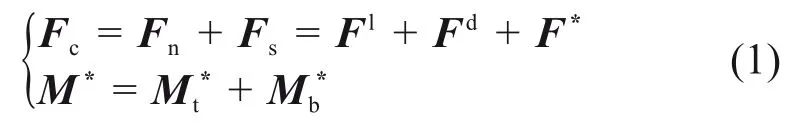
其中：

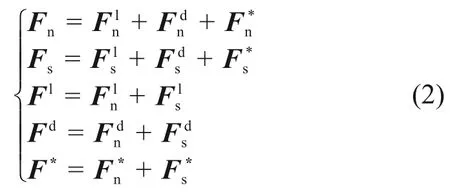
Fl为线性接触力，分解为法向力Fln和切向力Fls；Fd为黏滞阻尼力，分解为法向阻尼力Fdn和切向阻尼力Fds；F*为胶结接触力，分解为法向力F*n和切向力F*s。在每个计算循环内，线性接触力的法向分量Fln和切向分量Fls以增量形式更新的计算公式为：

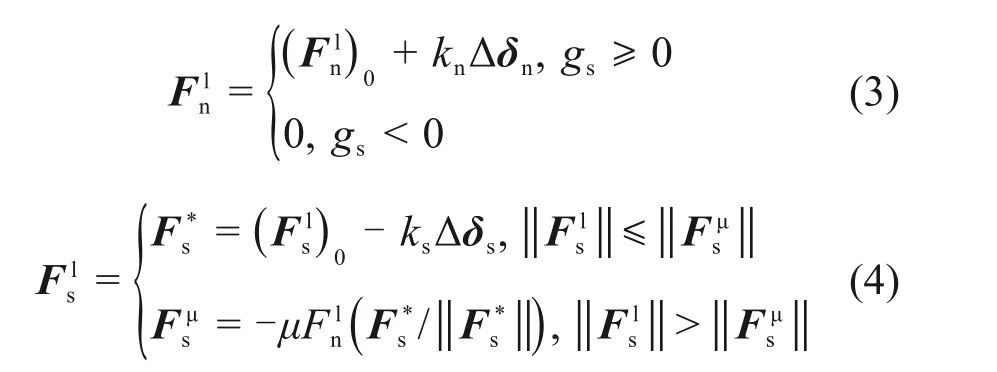
式中：(Fnl)0和(Fsl)0分别为当前计算循环内的初始法向力和初始切向力；Δδn和Δδs分别为法向和切向相对位移；F*s和Fμs分别为当前计算循环内颗粒间未产生滑动和产生滑动时的切向力。在每个计算循环内，胶结接触力的法向分量F*n和切向分量Fs*以增量形式更新的计算公式为：

式中：(Fn*)0和(Fs*)0为当前计算循环内的初始胶结法向力和初始胶结切向力；A*为胶结截面面积。在每个计算循环内，胶结力矩的扭矩分量M*t和弯矩分量M*b以增量形式更新的计算公式为：

式中：(Mb*)0和(Mt*)0为当前计算循环内的初始胶结弯矩和初始胶结扭矩；I*和J*分别为胶结截面的惯性矩和极惯性矩；Δθb和Δθt分别为相对弯曲转角增量和相对扭转角增量。

线性平行胶结模型中的胶结具有一定强度，如果胶结截面上的最大法向或切向应力超过了胶结强度，那么胶结失效，线性平行胶结模型退化为线性接触模型。图5所示为胶结截面上法向和切向应力的分布，用红点标识最大法向和切向应力点。胶结截面上的最大法向应力σ*n和最大切向应力τ*s计算式为

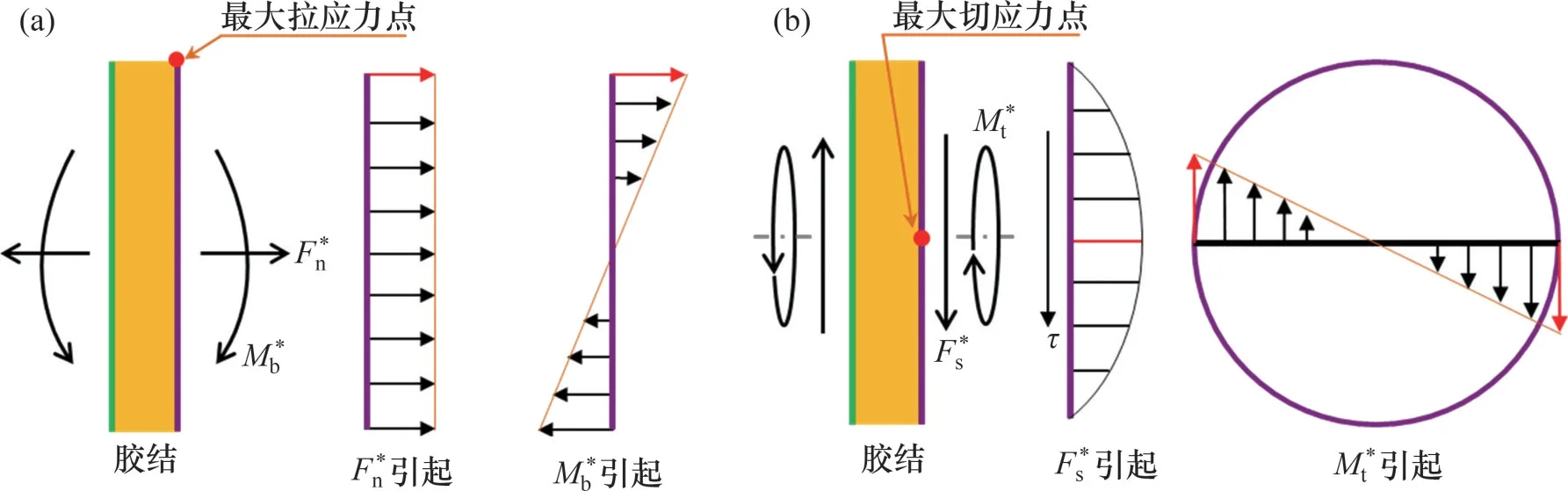
图5 线性平行胶结模型胶结平面上应力分布Fig.5 Stress distribution in bond plane of linear parallel bond model

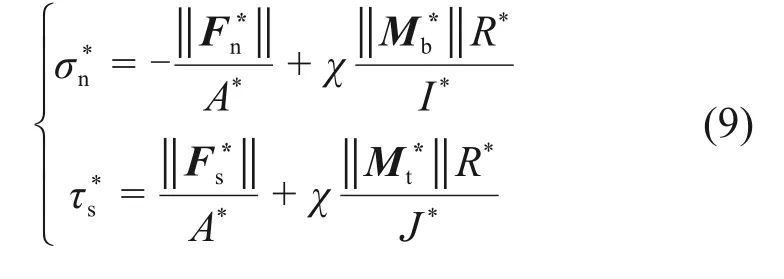
式中：R*为胶结半径；χ为力矩影响系数。如果最大法向应力超过了拉伸强度，那么胶结产生拉伸破坏；如果最大切向应力超过了剪切强度，那么胶结产生剪切破坏。拉伸强度σ*c按经验设定，剪切强度τ*c由黏聚力c*和内摩擦角φ*计算式为

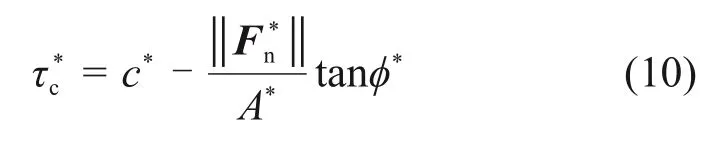
1.4 接触模型参数

在水合物沉积物的离散元模型中，存在线性和线性平行胶结2种接触模型，现将这2种接触模型的参数分为2个部分：

1)一部分是线性接触模型和线性平行胶结模型的线性部分参数，主要包括有效模量E、法向-切向刚度比κ、摩擦因数μ以及法向和切向临界阻尼系数βn和βs。

2)另一部分是线性平行胶结模型的胶结部分参数，主要包括胶结有效模量E*、胶结法向-切向刚度比κ*、胶结拉伸强度σ*c、胶结黏聚力c*以及摩擦角φ*。接触模型参数的标定流程比较繁琐，只将标定的接触模型参数总结在表1中。

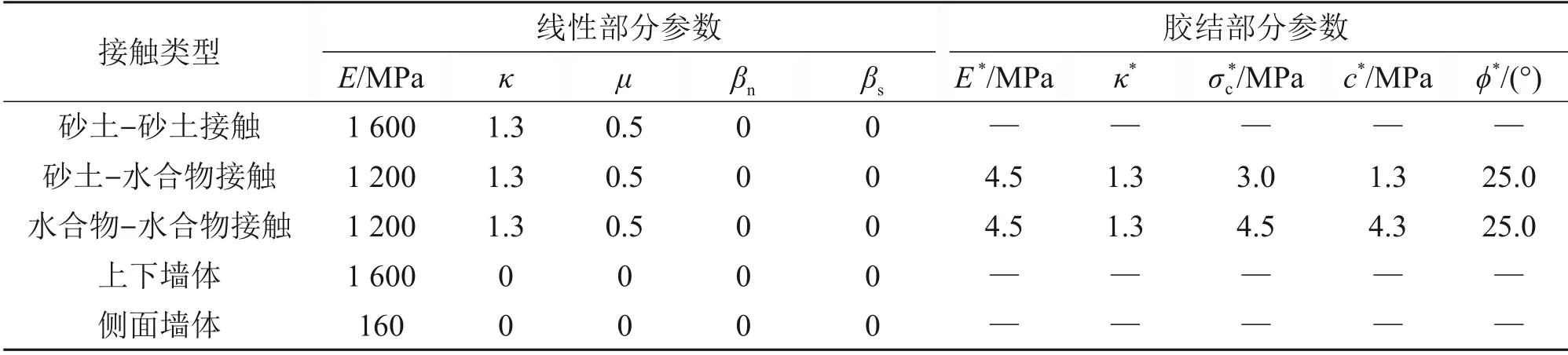
表1 接触模型参数Table 1 Contact model parameters

2 宏观力学特性分析

2.1 应力-应变-剪胀响应

在数值试验中，轴向应力由上下墙体与颗粒之间的相互作用力来计算，轴向应力减去围压得到偏应力；轴向应变由试样轴向变形计算得到；体积应变由试样的体积变化计算得到。偏应力q，轴向应变εa以及体积应变εv分别由下式计算：

式中：σ1为轴向应力；σ3为围压；F1和F2分别为上部墙体和下部墙体受到的接触力；r为上部墙体和下部墙体的截面半径；h0和h分别为试样加载前后的高度；V0和V分别为试样加载前后的体积。

图6所示为试样体积的计算方法。取某个应变状态下的试样举例说明，其中，试样加载前的体心位置取为O点。试样的体积V可以由5个部分体积计算得到，分别是O点与上下部墙体组成的圆锥体V1和V2、上下部墙体轴向运动扫掠过的圆柱体体积V3和V4以及O点与所有墙体三角形单元顶点组成的四面体Vi的总体积。假定四面体Vi的4个顶点分别为O(x0，y0，z0)，A(x1i，y1i，z1i)，B(x2i，y2i，z2i)和C(x3i，y3i，z3i)，那么试样体积的计算公式为

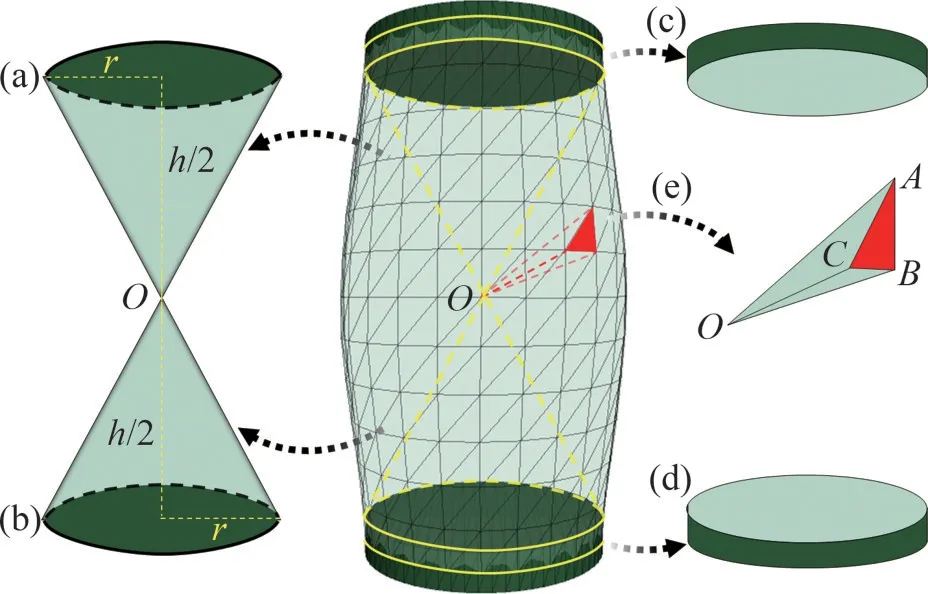
图6 某应变时试样体积计算方法Fig.6 Calculation method of sample volume at a strain

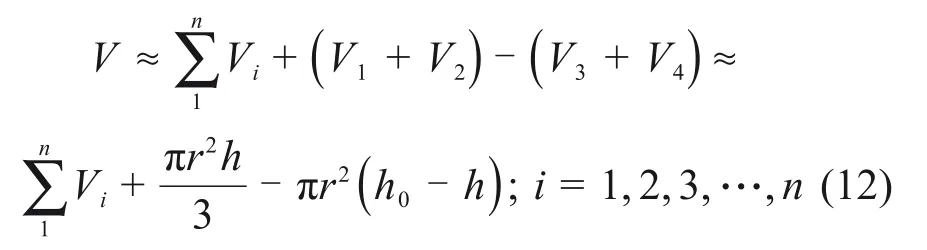
其中：

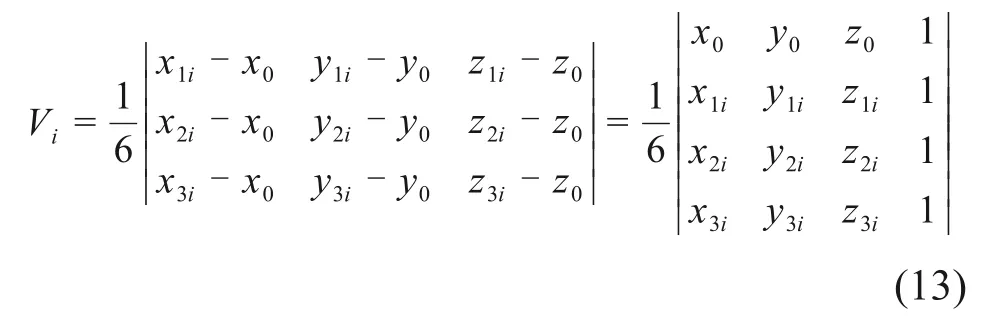
n为墙体三角形单元的数量。由此可以计算出试样体积，进而计算体积应变。该方法也可以用于膜柔性边界条件下的模型体积计算，只不过墙体三角形单元的顶点坐标需要替换为相邻的3个膜颗粒的中心坐标。

图7所示为在1.0 MPa 有效围压下不同水合物饱和度试样的应力-应变-剪胀曲线。由图7可见：数值试验可以模拟天然气水合物沉积物试样的强度和变形特性，主要体现在：

图7 不同水合物饱和度试样的应力-应变-剪胀曲线Fig.7 Stress-strain-dilatancy response of natural gas hydrate bearing samples with different hydrate saturations

1)应力-应变曲线为应变软化型；

2)水合物饱和度对试样的强度影响显著，水合物饱和度越大，刚度和强度越大；

3)试样表现出显著剪胀性，而且水合物饱和度越大，剪胀效应越明显。

2.2 变形破坏特征

颗粒材料产生屈服破坏时，应变往往会集中于某一局部区域，进而形成剪切带。水合物沉积物的应力-应变曲线是应变软化型，而应变软化过程是一种不稳定过程，常伴随着应变局部化(剪切带)的产生。从颗粒尺度来看，剪切带的萌生和发展伴随着颗粒转角的变化，而对于胶结材料而言，同时伴随着胶结的破坏。在物理试验中，难以获取试样内部颗粒层面的信息，而在离散元模拟中，这些信息很容易进行可视化分析。

图8所示为加载结束后的试样柔性边界上壳单元节点在xoz和yoz视图方向上的位移云图。由图8可见：壳单元节点的位移云图展现了试样的整体变形形态，能够体现试样整体的不均匀变形；不同水合物饱和度的试样最大的径向变形大约出现在轴向中间部位，外观上呈现鼓胀破坏形态。此外，水合物饱和度不同，试样的整体变形形态也有所不同。

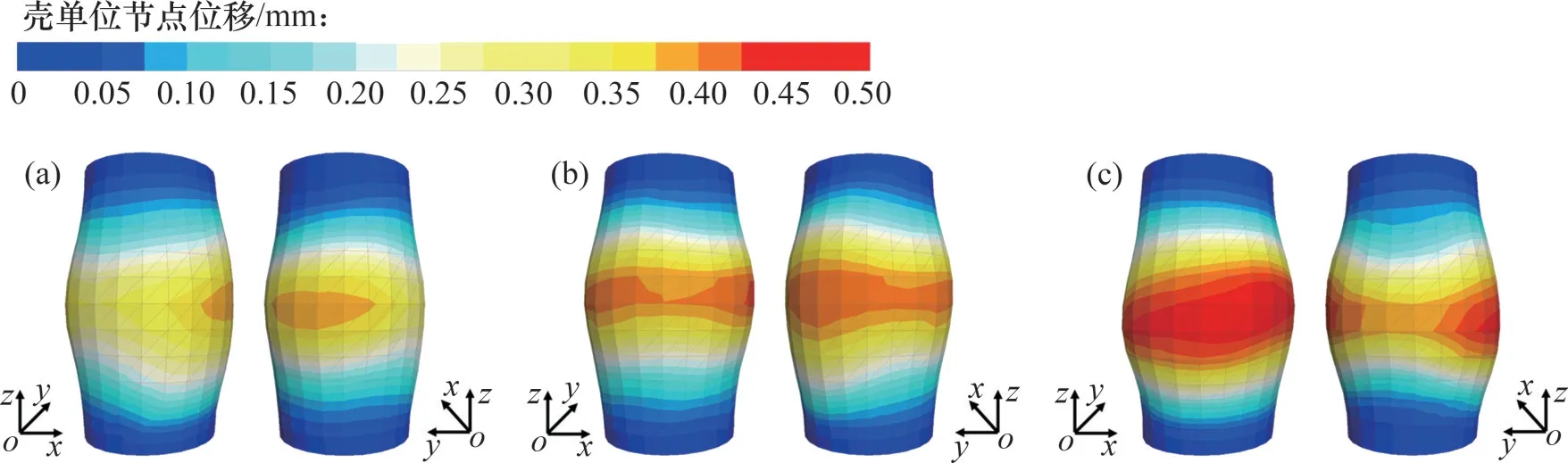
图8 不同水合物饱和度试样柔性边界上壳单元节点位移云图Fig.8 Nodal displacements of shell elements in flexible boundary of GHBS with different hydrate saturations

图9所示为试样内部颗粒的转角分布。由图9可见：水合物饱和度不同，试样内部局部变形破坏的形式不同。对于水合物饱和度为26%的试样，xoz剖面上具有2条交叉形剪切带，而yoz剖面上的剪切带形态不规则；对于水合物饱和度为40%的试样，xoz和yoz剖面上的剪切带均不规则；对于水合物饱和度为55%的试样，xoz剖面上呈现1 条斜向剪切带，而yoz剖面上具有2条交叉形剪切带。此外，剪切带内外颗粒的转角分布特征差异明显，呈现强烈的局部化特征。在剪切带附近位置，颗粒的转角最大，而在剪切带外部区域，颗粒的转角很小。

2.3 黏聚力和内摩擦角

尽管已有学者考虑了应变软化和体积剪胀等因素，在临界状态理论框架内提出了实用的水合物沉积物的本构模型，但是这些本构模型引入了物理意义不尽相同的参数，难以用统一的表达式去衡量水合物沉积物的强度指标。Mohr-Coulomb准则是一种经典的岩土强度准则，可以方便地评价水合物沉积物的强度参数。基于Mohr-Coulomb准则，岩土材料的剪切强度τ由黏聚力c和内摩擦角φ这2个力学指标决定，而且与破坏平面上的正应力σ有关，公式为

黏聚力反映了岩土颗粒间引力与斥力的综合作用，引力主要包括静电引力、范德华力、颗粒间的胶结、颗粒间接触点的化合键等，斥力主要包括静电斥力和双电层相互作用产生的斥力；内摩擦角反映了岩土的摩擦特性，主要包括岩土颗粒表面摩擦力和颗粒间的咬合作用。黏聚力和内摩擦角可以通过不同围压下的摩尔圆的包络线确定。图10所示为水合物饱和度分别为26%，40%和55%情况下，水合物沉积物的莫尔圆及其包络线，并由此可以确定黏聚力与摩擦角及水合物饱和度之间的关系，如图11所示。整体来说，数值模拟得到的内摩擦角和黏聚力在合理范围内。随着水合物饱和度从26%增加到55%，黏聚力从600 kPa 增加至1 000 kPa。相比较来说，水合物对内摩擦角的影响很小，随着水合物饱和度从26%增加到55%，内摩擦角从36°增加到42°。可以看出，水合物主要通过提高沉积物的黏聚力而提高剪切强度，而对内摩擦角的影响较小。该结论与现有的一些物理试验研究[28-32]的结果类似。

图10 不同水合物饱和度试样的莫尔圆和摩尔-库仑失效包络线Fig.10 Mohr's circles and Mohr-Coulomb failure envelop of GHBS with different hydrate saturation

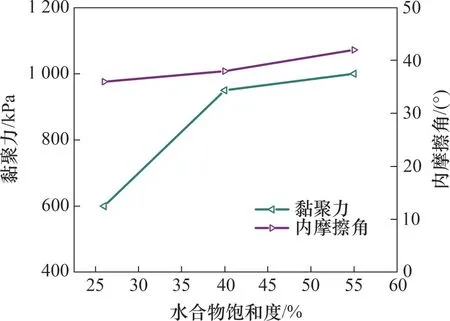
图11 不同水合物饱和度试样的黏聚力和内摩擦角Fig.11 Cohesion and internal friction angle of GHBS with different hydrate saturations

图12所示为物理试验与离散元数值试验得到的黏聚力和内摩擦角。由图12可见：即便是相同或相近的水合物饱和度情况下，黏聚力和内摩擦角也会有差别，这与沉积物的类型、试样制备方法、初始孔隙率以及试验条件等因素关系密切。总体来看，随着水合物饱和度增加，水合物沉积物的黏聚力增大，而内摩擦角变化不明显。

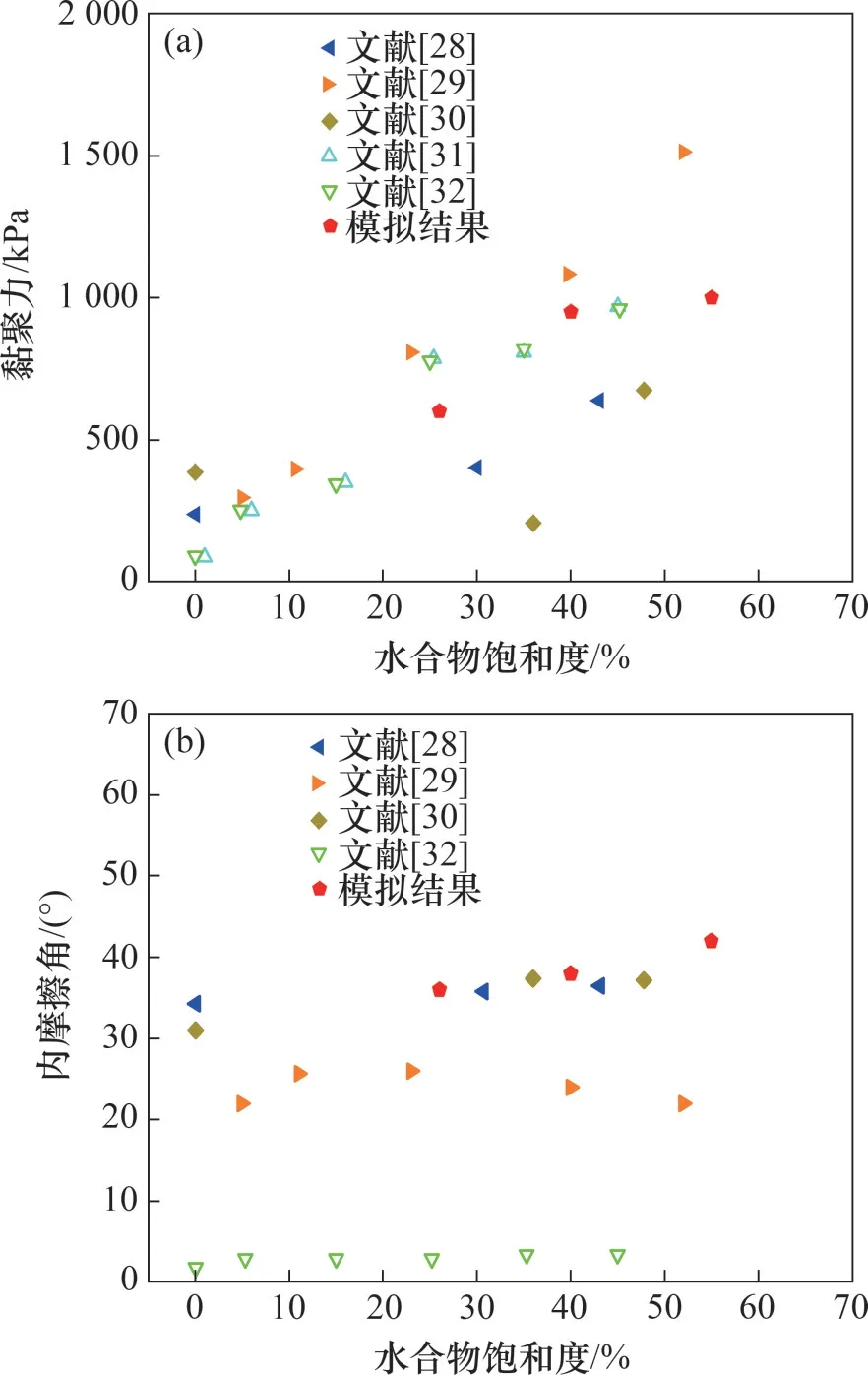
图12 黏聚力、内摩擦角与水合物饱和度的关系Fig.12 Cohesion and internal friction angle with respect to hydrate saturation

3 微细观机制分析

3.1 力链分析

颗粒材料是由众多离散单元组成的非连续介质，相邻颗粒间产生接触，形成了应力传递的路径，该路径通常呈准直线性的链状结构，称为力链。力链在尺度上介于颗粒单元与颗粒体系之间。在自身重力和外部荷载作用下，若干力链会产生分叉、合并和交叉，贯穿于颗粒材料内部，形成了复杂的力链网络，它的空间分布及其复杂的动力学响应主导了颗粒体系的力学性能[33]。

力链的定义没有得到广泛的共识，因此难以定量分析力链的结构及其演化行为。CAMPBELL等[34-35]认为力链是由若干应力集中的颗粒组成的准直线的颗粒串。SUN 等[36]提出了强力链的判别准则，认为强力链上的颗粒必须相邻，颗粒之间枝矢量角度的变化小于某个阈值，同时颗粒受到的接触力要大于所有接触力的平均值。PETERS等[37]提出了力链结构所需要具备的3个必要条件：

1)力链由3个或3个以上颗粒组成；

2)组成力链的颗粒为高应力颗粒，即颗粒的最小主应力的绝对值要大于所有颗粒最小主应力绝对值的平均值；

3)2 个相邻颗粒的枝矢量方向与他们2 个颗粒的最小主应力方向之间的夹角θ小于45°。

由这3个必要条件可以确定颗粒材料内部力链的识别流程。需要注意的是，因为主应力的符号以拉为正，因此，最小主应力为颗粒受到的最大压应力。付龙龙等[38-39]用该定义对二维情况下单一颗粒材料的力链演化行为进行了分析研究。

在外部荷载和重力作用下，颗粒材料内部的颗粒受到相邻若干颗粒的相互作用力，由此可以定义颗粒的应力张量[40]。在三维笛卡尔坐标系中，假如颗粒α和颗粒β相邻且属于同一力链，颗粒α的应力张量为σα，用分量形式可以表示为

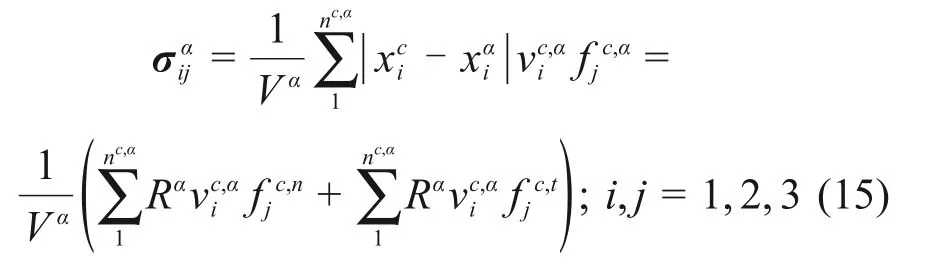
式中：Vα为颗粒α的体积；nc,α为作用在颗粒α上的接触数目；xci为接触矢量xc(定义为颗粒α的中心指向接触点的矢量)的分量；xαi为颗粒α中心坐标xα的分量；vc,αi为颗粒α的几何中心指向接触点的单位矢量vc,α的分量；fc,αi为接触力fc,α的分量；Rα为颗粒α的半径；fc,nj为接触力fc,α的法向分量；fc,tj为接触力fc,α的切向分量。

设应力张量σα的最小主应力为σα3，那么根据条件(2)可以得到

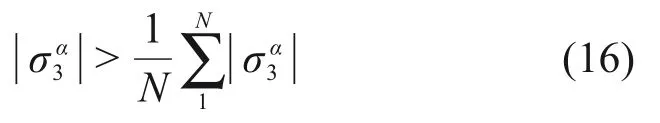
式中：N为颗粒的数量。

设σα3的方向矢量为v3(l3,m3,n3)，它的分量可以由应力张量σα的分量完全确定，由下式计算：

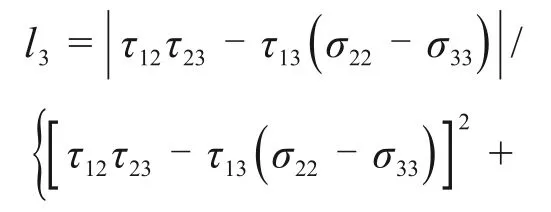
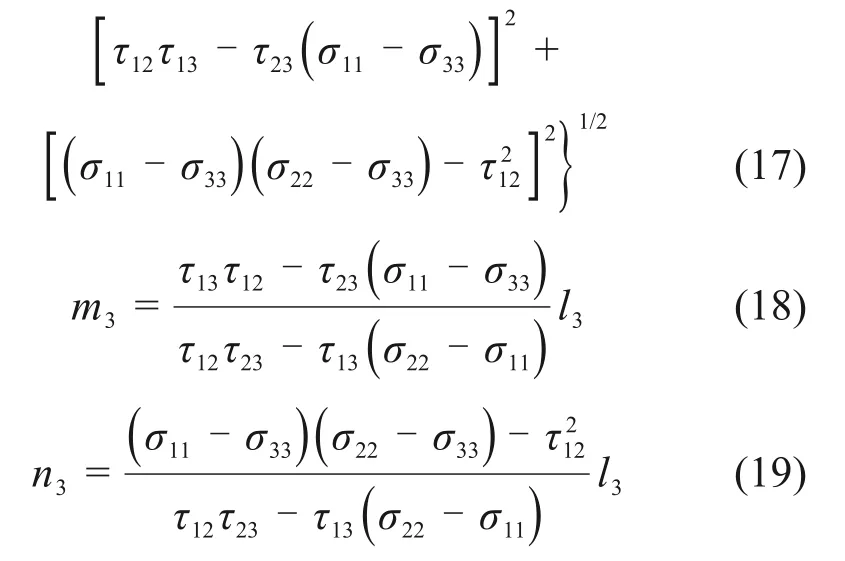
式中：σii(i=1，2，3)是σα主对角线上的分量；τij(i,j=1，2，3)是σα非主对角线上的分量。

按照条件(3)，若以颗粒α为基准，并将枝矢量uβ,α定义为颗粒α的中心指向颗粒β的中心的矢量，那么颗粒α的最小主应力的方向矢量nα3需要满足式(20)，即

反之，以颗粒β为基准，颗粒β的最小主应力的方向矢量与它们的枝矢量-uβ,α仍需满足式(20)。

图13所示为不同水合物饱和度试样内部高应力颗粒数量的演化过程。由图13可见：随着轴向应变增大，高应力颗粒数量和高应力水合物颗粒数量逐渐减小，而高应力砂土颗粒数量变化不大。此外，水合物饱和度越高，高应力颗粒和高应力水合物颗粒的数量越多，而不同水合物饱和度试样内部高应力砂土颗粒的数量差别不大。

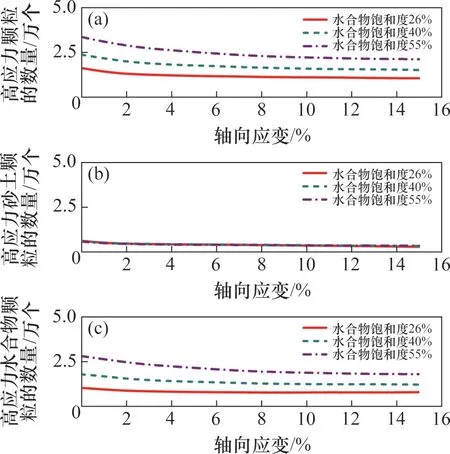
图13 不同水合物饱和度试样内部高应力颗粒的数量Fig.13 Quantity of particles with high stress in GHBS samples with different hydrate saturations

图14所示为不同水合物饱和度试样内部力链颗粒数量的演化过程。由图14可见：只有部分高应力颗粒组成了力链，力链颗粒数目占高应力颗粒数量的50%～60%。随着轴向应变增大，力链颗粒的演化规律与高应力颗粒的演化规律类似。随着轴向应变增大，力链颗粒和力链中水合物颗粒的数量逐渐减小，而力链中的砂土颗粒数量变化不大。此外，水合物饱和度越高，力链颗粒和力链中的水合物颗粒的数量越多，而不同水合物饱和度试样内部力链中的砂土颗粒的数量差别不大。

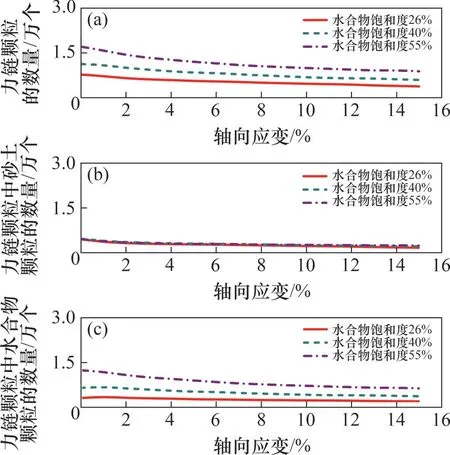
图14 不同水合物饱和度试样内部力链颗粒数量Fig.14 Quantity of particles in force chains of GHBS samples with different hydrate saturations

图15所示为不同水合物饱和度试样内部力链的数量与轴向应变的关系。由图15可见：随着轴向应变增大，力链的数量逐渐减少；水合物饱和度越大，试样内部力链的数量越多。图16所示为不同水合物饱和度试样内部力链数量与力链长度的关系。由图16可见：对于某一水合物饱和度的试样来说，长度在3～6个颗粒的力链约占所有力链数量的90%以上，长度大于等于7个颗粒的力链很少而且它们的数量具有随机性；力链的长度越短，它的数量越多；长度为3～7个颗粒的力链数量随着轴向应变增大而显著减少。此外，水合物饱和度越大时，试样内部长度为3～7个颗粒的力链数量越大，而长度大于7个颗粒的力链数量没有呈现规律性。此外，力链长度最大为20 个颗粒，出现在水合物饱和度为55%的试样内部。因此，水合物颗粒参与了水合物沉积物内部的应力传递过程，水合物饱和度越大，水合物所承担的外部荷载越多。这从力链的角度解释了水合物影响水合物沉积物强度的细观机制。

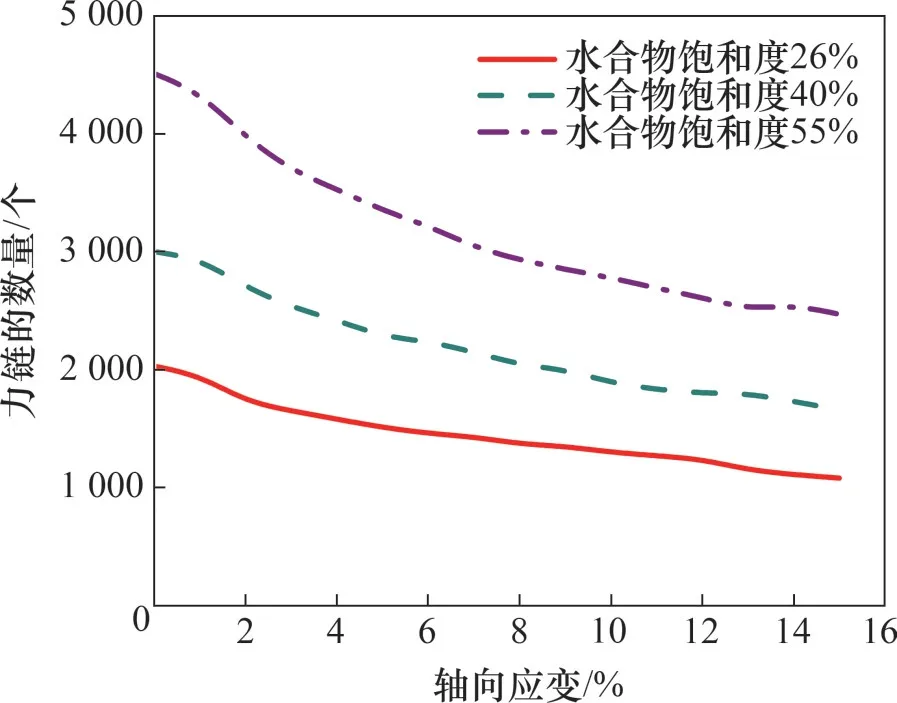
图15 不同水合物饱和度试样内部力链数量与应变的关系Fig.15 Quantity of force chains with respect to axial strain in GHBS samples with different hydrate saturations

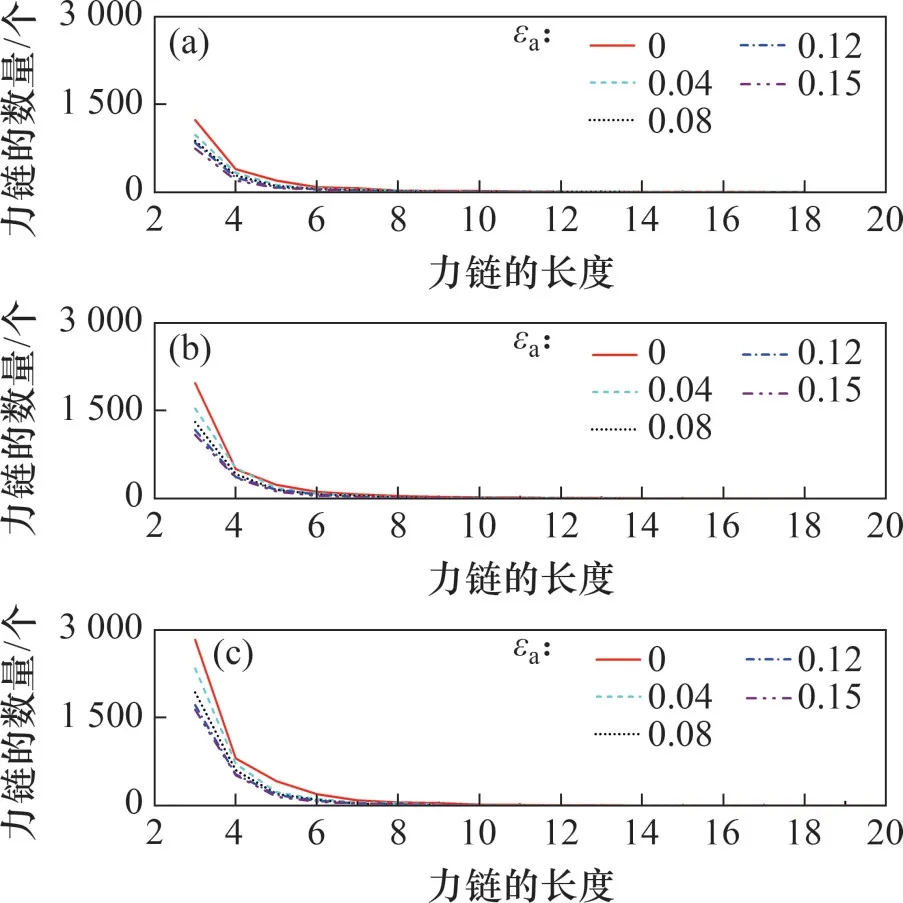
图16 不同轴向应变下力链数量与力链长度的关系Fig.16 Quantity of force chains with length of force chain at different axial strains

3.2 能量耗散机制

从热力学角度来看，水合物沉积物试样受力变形过程可以认为是一种能量的不可逆耗散过程。能量耗散机制是解释颗粒材料微细观力学机制的一种重要方法。根据能量守恒定律，从外界通过墙体输入的边界能量Ew转化为试样内部的体力功Eb、摩擦耗能Ef、弹性应变能Ec、胶结应变能Ep、阻尼能Ed以及颗粒的动能Ek，由式(21)计算

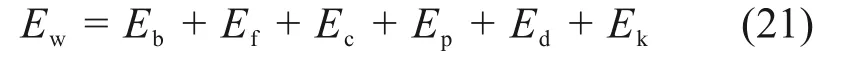
在模拟中不考虑重力，因此忽略体力功Eb。在准静态加载过程中，动能Ek和阻尼能Ed很小，可以忽略。边界能量是系统的输入能量，来源于作用在墙体上的外部的合力和合力矩所做的功，在三轴试验过程中，边界能量来自于偏应力和有效围压做的功，边界能量Ew由式(22)计算

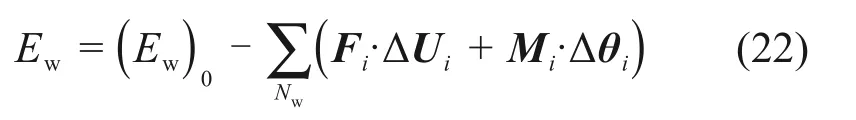
式中：(Ew)0为当前时步开始时的边界能量；Nw为墙体的数量；Fi和Mi分别为作用在墙体上的合力和合力矩；ΔUi和Δθi分别为墙体的位移和转角。

摩擦耗能主要来源于颗粒间的滑动摩擦，弹性应变能主要储存于接触模型的线性部分，而胶结应变能主要储存于接触模型的胶结部分，摩擦耗能Ef、弹性应变能Ec和胶结应变能Ep分别由式(23)～(25)计算[27]

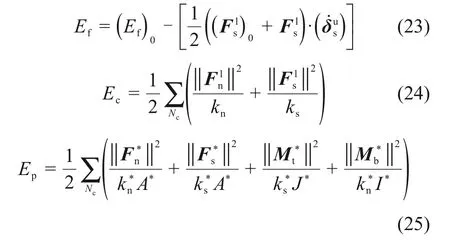
式中：(Ef)0为当前时步开始时的摩擦耗能；Nc为接触数目；为切向相对位移中的滑动部分。

图17所示为不同水合物饱和度试样内部不同类型能量的演化过程。由图17可见：不同水合物饱和度试样内部不同类型能量的演化规律类似。具体来说，随着轴向应变增大，边界能量逐渐增加；在相同的轴向应变下，水合物饱和度越高，边界能量越大，同时，摩擦耗能、弹性应变能和胶结应变能也越大，这说明水合物饱和度越高，试样所需要的能量越大；在准静态过程中，动能和阻尼能可以忽略，因此，边界能量主要转化为摩擦耗能、弹性应变能和胶结应变能。摩擦耗能基本呈线性增长趋势；弹性应变能随着轴向应变增大而增大，当达到最大值后缓慢减小；胶结应变能在加载初期为0，随着轴向应变增大而增大。

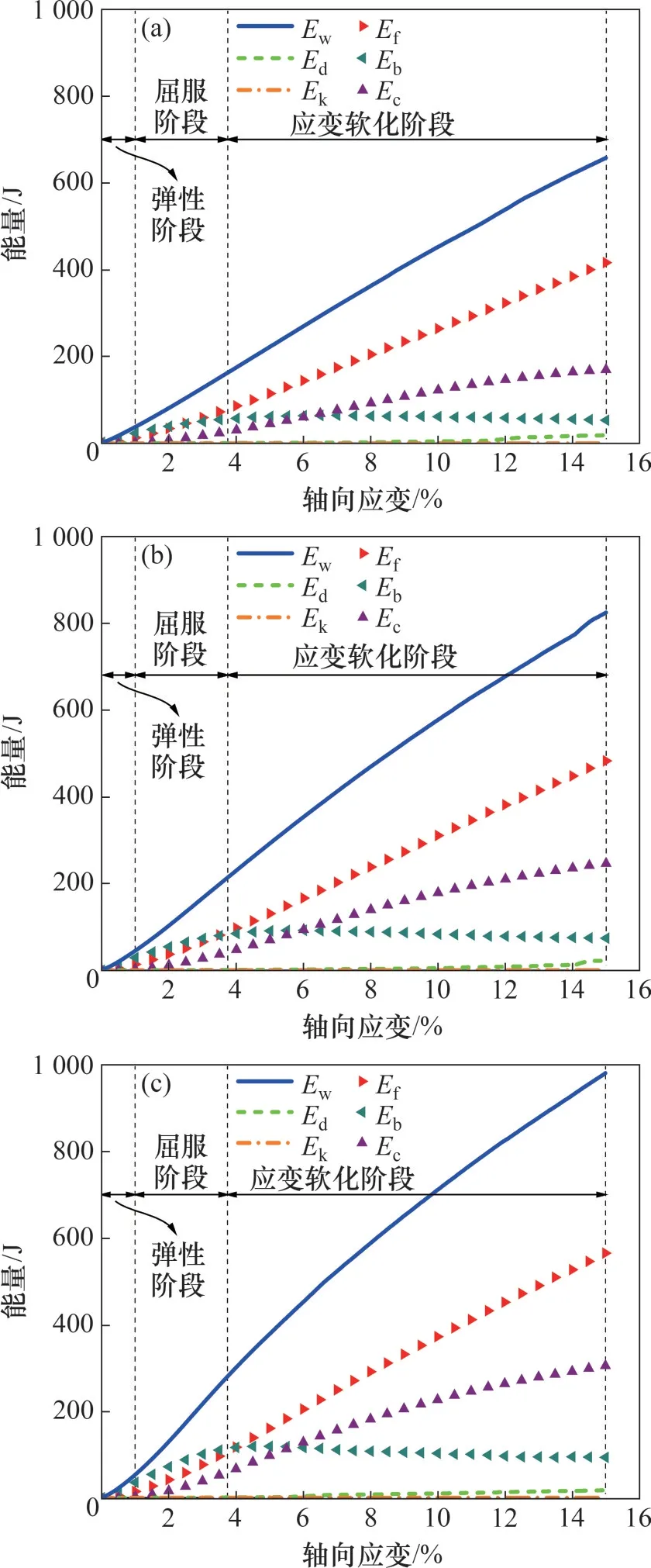
图17 不同水合物饱和度试样内部不同类型能量的演化过程Fig.17 Evolution of different types of energy in GHBS with different hydrate saturations

结合偏应力-轴向应变曲线，可以将试样的变形阶段大体分为弹性阶段、屈服阶段和应变软化3个阶段。

1)在弹性阶段，颗粒间的摩擦滑移很少，胶结也没有破坏，因此，边界能量主要转化为弹性应变能；

2)在屈服阶段，颗粒间产生摩擦滑移，而且胶结开始破坏，此时边界能量主要转化为弹性应变能和摩擦耗能，同时，胶结应变能开始慢慢累积，需要注意的是，弹性应变能在峰值应力附近达到最大值；

3)在应变软化阶段，边界能量主要转化为摩擦耗能，胶结应变能逐渐增加并超过弹性应变能，而弹性应变能缓慢减小，这意味着在该阶段试样的强度主要由压应力作用下的颗粒摩擦的抗剪应力和颗粒的胶结提供。

如前所述，水合物沉积物试样内部存在3种接触集合，包括砂土-砂土、砂土-水合物和水合物-水合物接触集合，不同的接触集合设置了不同接触模型，不同能量由不同的接触集合储存和耗散。图18～20所示分别为不同接触集合的摩擦耗能、弹性应变能和胶结应变能的演化过程。从图18可见：相比于水合物-水合物接触，摩擦耗能主要在砂土-砂土和砂土-水合物接触处产生；水合物饱和度越高，这3种接触处的摩擦耗能也越大，但在数值上差别不大。从图19可见：相比较于水合物-水合物接触集合，弹性应变能主要储存在砂土-砂土接触集合和砂土-水合物接触集合；不同水合物饱和度试样内部砂土-砂土接触集合储存的弹性应变能差别不大；水合物饱和度越大，试样内部砂土-水合物接触集合储存的弹性应变能越大。从图20可见：胶结应变能基本由砂土-水合物接触集合储存，相比来说，水合物-水合物接触集合储存的胶结应变能可以忽略；水合物饱和度越大，试样内部砂土-水合物接触集合储存的胶结应变能越大。

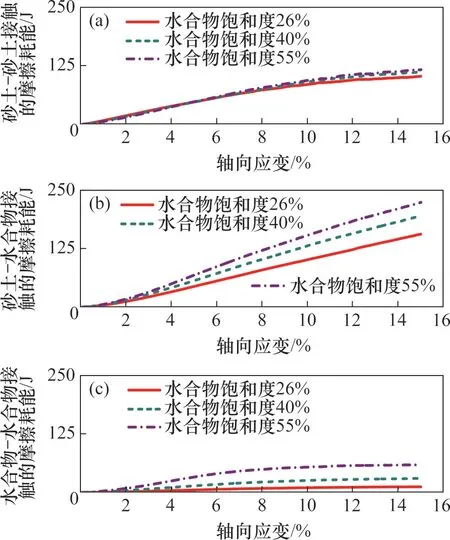
图18 不同接触集合的摩擦耗能的演化过程Fig.18 Evolution of friction energy for different contact subsets in GHBS with different hydrate saturations

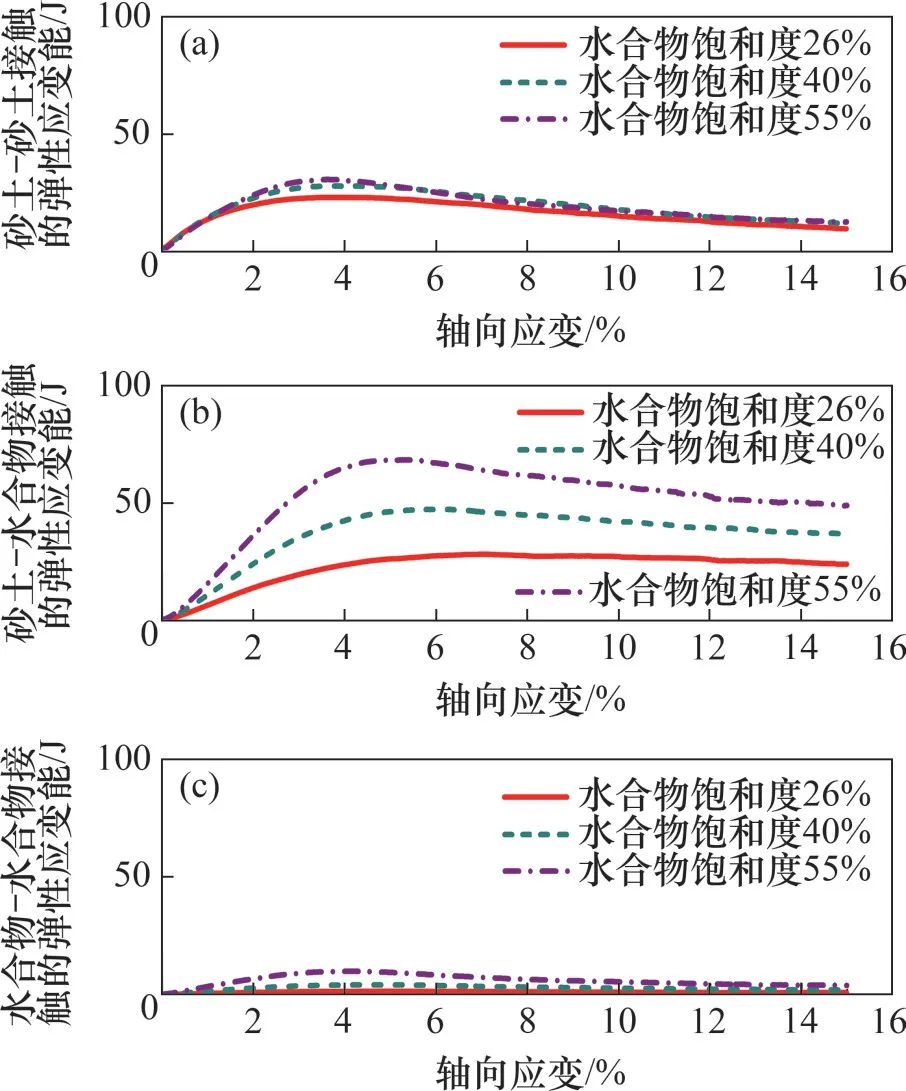
图19 不同接触集合的弹性应变能的演化过程Fig.19 Evolution of strain energy for different contact subsets in GHBS with different hydrate saturations

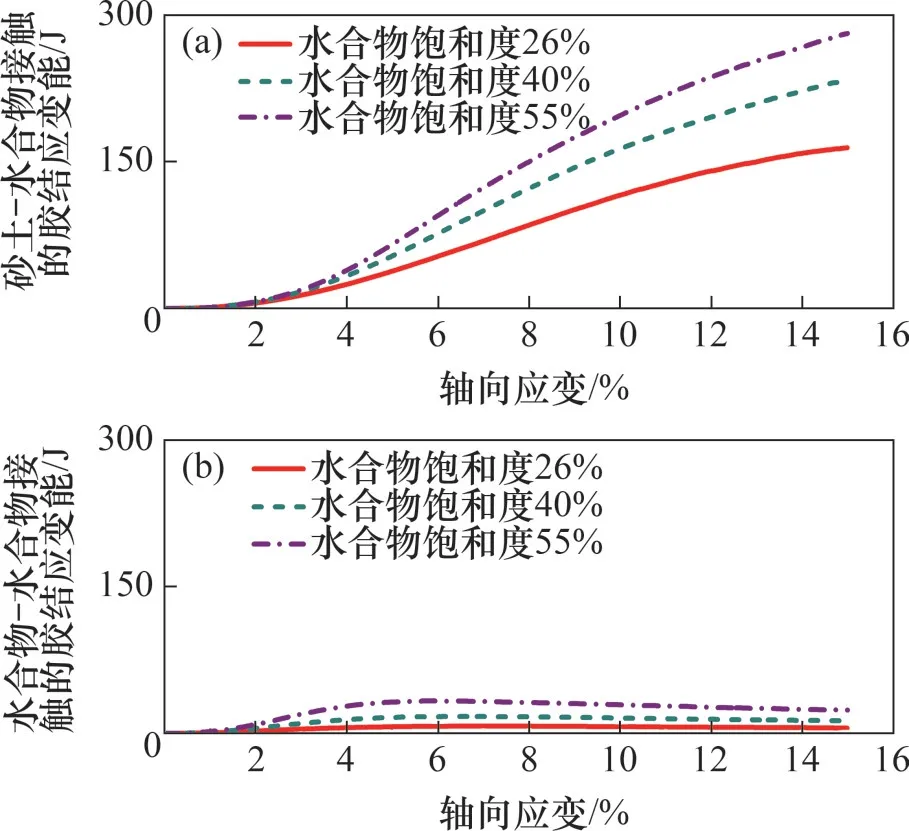
图20 不同接触集合的胶结应变能的演化过程Fig.20 Evolution of bond strain energy for different contact subsets in GHBS with different hydrate saturations

从以上分析可知：水合物饱和度越高，在相同的应变条件下，输入的边界能量越大，摩擦消耗的能量越大，弹性应变能和胶结应变能储存得越多；水合物饱和度越高，在砂土-水合物接触处，因摩擦而消耗的能量越多，弹性应变能和胶结应变能储存得越多，而水合物-水合物接触在能量耗散过程中起到的作用很小。因此，从能量角度来说，水合物主要是通过砂土-水合物接触以摩擦耗能、弹性应变能和胶结应变能的形式对水合物沉积物力学特性产生影响。

4 结论

1)采用线性平行黏结模型考虑水合物的胶结效应，并标定合适的接触模型参数，离散元数值试验能够有效地再现胶结型天然气水合物沉积物应力-应变-剪胀响应。

2)水合物主要通过增大沉积物的黏聚力来提高胶结型水合物沉积物的强度。此外，水合物沉积物的黏聚力和内摩擦角不仅与水合物饱和度相关，而且与砂土的类型、制样方法、初始孔隙率等因素也有关联。

3)采用Wall-Zone界面耦合方法可以创建离散元数值试验中的柔性边界条件，能够捕捉到试样的非均匀变形破坏特征。不同水合物饱和度试样最大的径向变形大约出现在试样的轴向中间位置，而且不同水合物饱和度试样内部局部变形形式不同。此外，提出了一种试样在非均匀变形时计算体积的方法。

4)从力链角度来说，水合物参与了胶结型水合物沉积物试样内部力链的构成，与砂土骨架一起组成力链并承担外部载荷；从能量角度来说，水合物主要通过砂土-水合物接触以摩擦耗能、弹性应变能和胶结应变能的形式对水合物沉积物力学特性产生影响。