致密气井稳产时间预测模型及应用

张磊，王永科，乔向阳，倪军，吴克柳，辛翠平，张涛,3，康宇龙，许阳，冯婷婷

(1.陕西延长石油(集团) 有限责任公司研究院，陕西西安，710065；2.中国石油大学(北京) 油气资源与探测国家重点实验室，北京，102249；3.西南石油大学油气藏地质与开发国家重点实验室，四川成都，610500；4.中国石油集团测井有限公司生产测井中心，陕西西安，710201)

致密气藏开发潜力巨大[1-4]，开发井数量多，通常采用定产降压的方式进行生产，在开发过程中普遍表现出低产气、低产水和低效益等特征。如何经济、准确预测气井稳产时间，进而指导产量优化，是实现致密气藏低成本开发和长期稳产的核心问题。

稳产包括气藏稳产和气井稳产，气藏稳产由气井稳产决定。关于气藏稳产的研究较多，如：NADERI 等[5-7]对水驱气藏的稳产进行了研究；LASDON等[8]对干气藏的稳产进行了研究；IZUWA等[9]对凝析气藏的稳产进行了研究；冀光等[10-11]对致密气藏的稳产进行了研究；贾爱林等[12-14]对碳酸盐岩气藏的稳产进行了研究，这些研究的方向主要集中在稳产对策和开发技术等方面。气井稳产时间预测方法包括矿场经验法和理论计算法。矿场经验法通过拟合油套压的下降趋势进行预测，该方法简单、快速，但预测精度相对较低，无法精准指导气井的产量优化。基于此，一些学者开展了关于理论计算法的研究，如：张宗林等[15-16]采用定产降压试验和数值模拟方法对气井的产量优化进行了研究；洪舒娜等[17]从有限导流垂直裂缝不稳定渗流模型出发，创建了一种预测压裂气井稳产时间的简便方法；李波等[18]通过正交实验评价了水平井的产量影响因素；郭春秋等[19]通过联立气井产能方程和物质平衡方程，推导了采气速度和自然稳产期的计算模型；冯曦等[20]通过耦合产能方程、井筒管流和井控储量，绘制了反应气井稳产能力的关系图；李颖川等[21]采用节点系统分析，建立了产水气井的优化配产模型；史海东等[22]基于物质平衡方程和产能公式，推导了异常高压气藏的自然稳产期预测模型。考虑到致密气藏的开发特征，将上述方法直接用于致密气藏的稳产时间预测和产量优化均存在一定的应用局限性。

基于前人的研究成果，本文作者以气液两相流井筒压力梯度方程和定容气驱产水气藏物质平衡方程为基础，以井口最低外输压力为约束条件，依次建立产水气井的井底流压解析模型、平均地层压力计算模型和稳产时间预测模型，进而采用数值模拟验证模型的准确性，最后通过实际产水气井产量优化论证模型的可靠性。

1 模型建立

气井生产是一个从产层到井底再到井口的协调系统，井口配产量决定气井的稳产时间，故可采用“井口—井底—产层”的逆向推演思路，建立产水气井的稳产时间预测模型。

1.1 井底流压

在致密气藏开发过程中，气井的产水量和产气量均较低，动能压力梯度相比重力压力梯度和摩阻压力梯度很小，可以忽略，故气液两相流井筒压力梯度方程为[23-27]

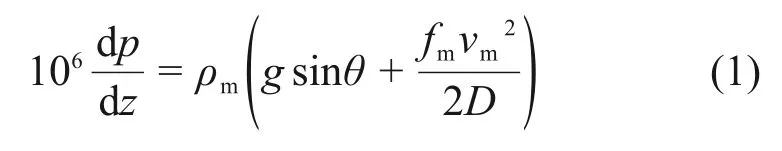
式中：p为井筒压力，MPa；z为任意点的斜深，取井口z=0 m；ρm为气液两相混合物密度，kg/m3；g为重力加速度，9.81 m/s2；θ为管柱的倾斜角，(°)；fm为气液两相混合物摩阻系数；vm为气液两相混合物流速，m/s；D为管柱内径，m。

气液两相混合物密度可表示为

式中：ρL为液体密度，kg/m3；λL为无滑脱持液率；ρg为气相密度，kg/m3。

定义含水修正系数为

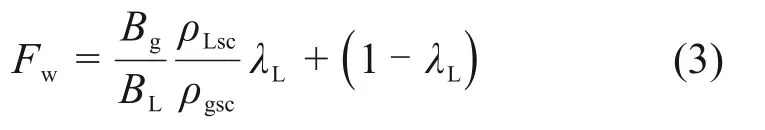
式中：Fw为含水修正系数；BL为液相体积系数；ρLsc为标准状态下的液相密度，对于水，ρLsc=1 000 kg/m3；ρgsc为标准状态下的气相密度，kg/m3。

气相体积系数的表达式为

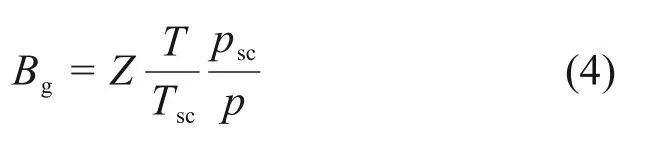
式中：Bg为气相体积系数；Z为气体偏差系数；T为热力学温度，K；Tsc为标准状态的温度，Tsc=293 K；psc为标准状态下的压力，psc=0.101 MPa。

将式(3)和式(4)代入式(2)，得到气液两相混合物密度的表达式：

假设井筒中气液两相之间不存在滑脱效应，得到气液两相混合物流速的表达式：

式中：vgsc为标准状态下的气体流速，m/s；qsc为标准状态下的产气量，104m3/d；A为生产管柱截面积，A=πD2/4，m2。

将式(5)和式(6)代入式(1)，得

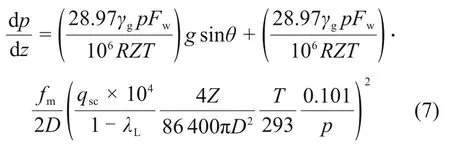
由于T和λL随着z变化，Z和Fw随着p变化，为便于积分，采用井筒管流模型简化思路，对温度和偏差系数取平均值，同时对持液率、气相体积系数和含水修正系数取平均值：

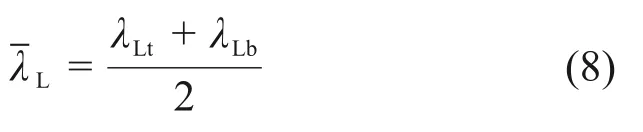
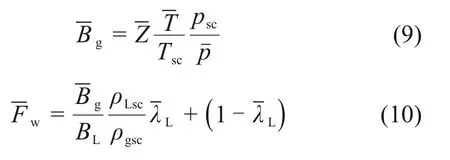
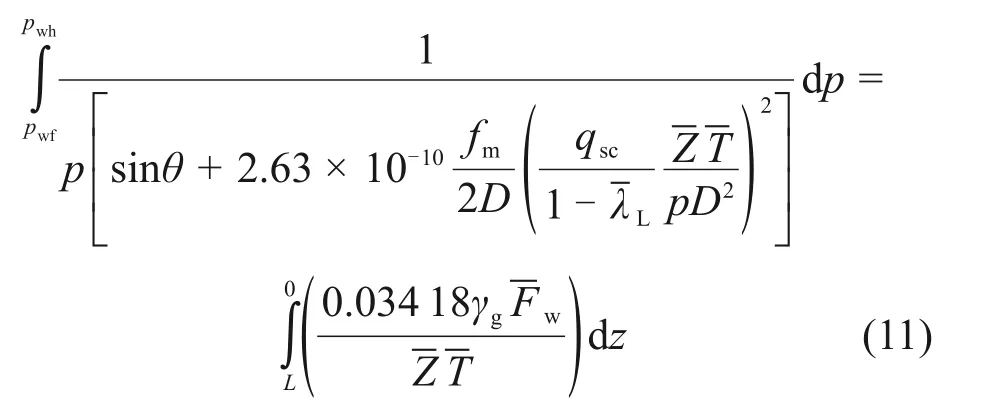
式中：pwf为井底流压，MPa；pwh为井口油压，MPa；L为产层底部斜深，m。

求解式(11)的积分，得到井底流压的表达式：

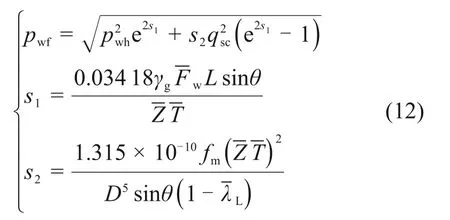
式中：s1和s2为计算指数。根据式(12)，可迭代计算pwh对应的pwf。

1.2 平均地层压力

考虑到致密气藏中普遍存在气水两相，参照定容气驱气藏的物质平衡方程，建立定容气驱产水气藏的物质平衡方程：

式中：G为地面标准条件下的天然气原始地质储量，104m3；Bgi为原始地层条件下的天然气体积系数；W为地面标准条件下的地层水原始地质储量，104m3；Bwi为原始地层条件下的地层水体积系数；Gp为地面标准条件下的天然气累积采出量，104m3；Bgr为目前地层条件下的天然气体积系数；Wp为地面标准条件下的地层水累积采出量，104m3；Bwr为目前地层条件下的地层水体积系数。

对式(13)进行推导，得到

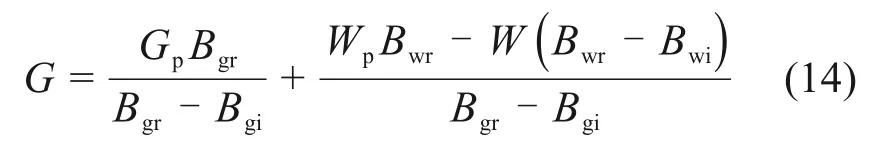
假设气藏在开采过程中温度保持不变，根据气相体积系数的表达式(4)，推导得到

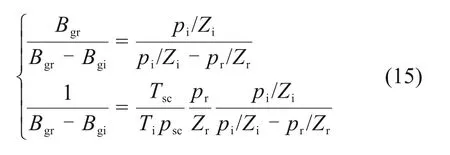
式中：pi为原始地层压力，MPa；Zi为原始地层压力下的偏差系数；pr为目前平均地层压力，MPa；Zr为目前地层压力下的偏差系数。

将式(15)代入到式(14)，推导得到

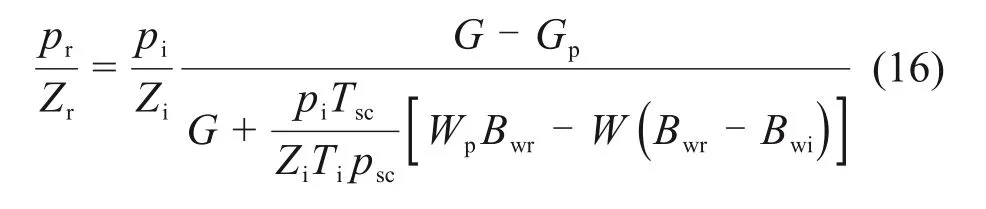
天然气原始地质储量和地层水原始地质储量可表示为：

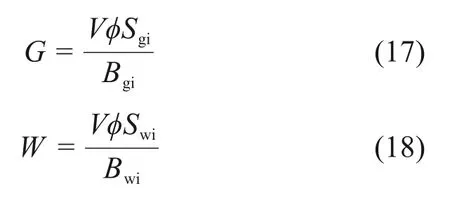
式中：V为储层体积，104m3；φ为孔隙度；Sgi为原始含气饱和度；Swi为原始含水饱和度。

由式(17)和式(18)，推导得到

将式(19)代入式(16)，推导得到定容气驱产水气藏的物质平衡方程：

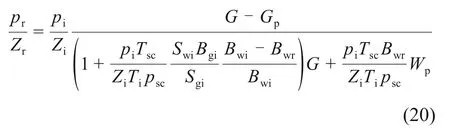
定义

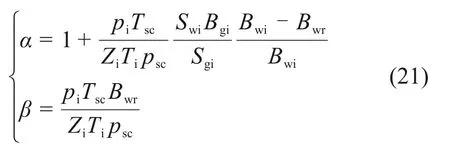
式中：α为天然气原始地质储量的修正系数；β为地层水累积采出量的修正系数。

将式(21)代入式(20)，定容气驱产水气藏的物质平衡方程变为

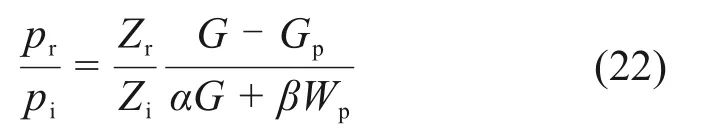
当Wp等于0时，式(22)就变成定容气驱气藏的物质平衡方程，故式(22)适用于定容气驱气藏和定容气驱产水气藏，但并不适用于水驱气藏、凝析气藏和异常高压气藏等其他类型的气藏。

对于时刻j和时刻j+1的物质平衡方程，存在

式中：pr(j+1)为j+1 时刻的平均地层压力，MPa；prj为j时刻的平均地层压力，MPa；Zr(j+1)为j+1时刻平均地层压力下的偏差系数；Zrj为j时刻平均地层压力下的偏差系数；Gp(j+1)为j+1 时刻的累积采出气量，104m3；Gpj为j时刻的累积采出气量，104m3；αj+1为j+1时刻的天然气原始地质储量修正系数；αj为j时刻的天然气原始地质储量修正系数；βj+1为j+1时刻的目前累积采出水量修正系数；βj为j时刻的目前累积采出水量修正系数；Wp(j+1)为j+1时刻的累积采出水量，104m3；Wpj为j时刻的累积采出水量，104m3。

当j和j+1 为相邻时刻时，进行如下简化：1)根据Bwr随p的变化规律，可认为Bw(j+1)≈Bwj，统一采用Bwj，进而得到αj+1≈αj，βj+1≈βj；2)对于定容气驱产水气藏，产出水来自气藏孔喉中的原始地层水和凝析水，日产水量极低，可认为Wp(j+1)≈Wpj，统一采用Wpj；3)根据Z随p的变化规律，可认为Zr(j+1)≈Zrj，统一采用Zrj。

将αj+1≈αj，βj+1≈βj，Wp(j+1)≈Wpj和Zr(j+1)≈Zrj代入式(23)，得到

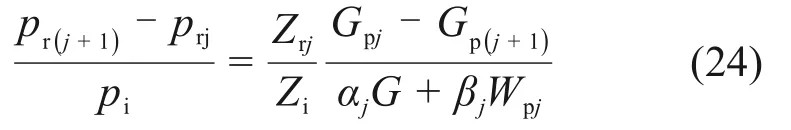
根据渗流力学原理[28]可知：1)定容气驱气藏以定产量生产时，地层压力传播很快进入拟稳态，井底流压与边界压力的下降速率相同；2)边界压力可近似等于平均地层压力。可以得到井底流压与平均地层压力的下降速率相同：

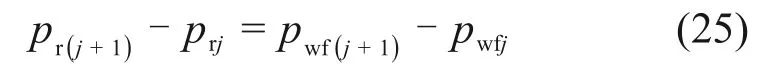
式中：pwf(j+1)为j+1 时刻的井底流压，MPa；pwfj为j时刻的井底流压，MPa。

将式(25)代入式(24)，经过推导，得到

将式(26)代入j时刻的产水气藏的物质平衡方程，经过推导，得到产水气井的平均地层压力：

式中：Zrj，αj和βj均为prj的函数。根据式(12)计算得到pwfj和pwf(j+1)后，代入试气数据和井口生产数据，可采用迭代方式计算pwfj对应的prj：首先赋予prj对应的迭代初值，根据迭代初值依次计算Zrj，αj，βj和prj，进而计算prj与迭代初值之间的相对误差，若相对误差满足计算要求，则迭代终止；若相对误差不满足计算要求，则将计算得到的prj作为迭代初值，继续迭代，直至相对误差满足计算要求。最后根据式(26)计算得到G。

1.3 稳产时间预测

当气井以定产量进行生产时，生产压差和动态控制储量保持不变，因此，可根据生产阶段的生产数据，预测气井未来的生产量。根据式(25)，生产压差为常数，可根据气井生产数据计算得

式中：C(qsc)为气井以qsc定产量生产时的生产压差，MPa。

当井口压力达到最低外输压力时，气井的自然稳产期结束，此时的井底流压达到自然稳产期的最低举升压力，平均地层压力达到自然稳产期的最低产出压力，根据式(12)和式(28)，得到：

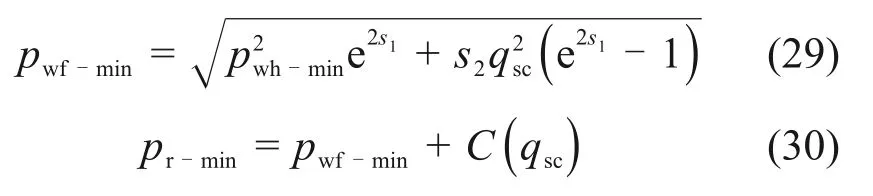
式中：pwf-min为自然稳产期的最低井底流压，MPa；pwh-min为最低外输井口压力，MPa；pr-min为自然稳产期的最低平均地层压力，MPa。

当pr达到pr-min时，物质平衡方程式(22)变为

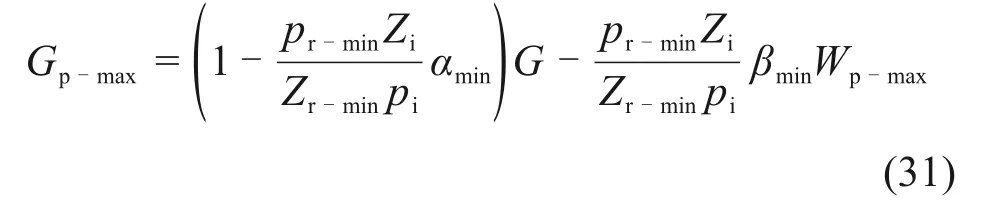
式中：Gp-max为自然稳产期末的累积采出气量，104m3；αmin为自然稳产期末的天然气原始地质储量修正系数；Zr-min为自然稳产期末的最低平均地层压力下的偏差系数；βmin为自然稳产期末的累积采出水量修正系数；Wp-max为自然稳产期末的累积采出水量，104m3。

定义

式中：γ为自然稳产期末的修正系数。

将式(32)代入式(31)，得到自然稳产期末的物质平衡方程：

Gp-max可表示为

式中：Gp为地面标准条件下的累积采出气量，104m3；tF为气井的预测稳产时间，d。

气井产水量的变化规律复杂，准确计算Wp-max较为困难。在致密气井定产量生产过程中，产水量和水气比在工程计算中基本保持稳定，可采用平均产水量进行预测，则Wp-max可近似表示为

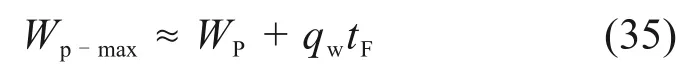
式中：WP为地面标准条件下的累积采出水量，104m3；qw为标准状态下的平均产水量，qw=WP/tP，104m3/d；tP为气井的实际稳产时间，d。

将式(34)和式(35)代入式(33)，经过推导，得到稳产时间预测模型：

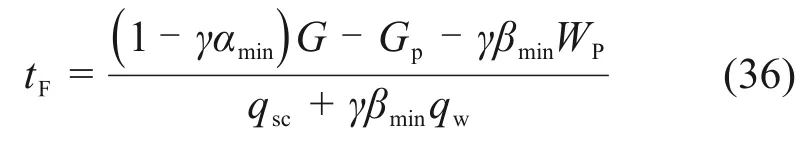
在实际气藏开发过程中，随着气井产量制度改变，单井动态控制储量随之发生变化。对于已经形成一定井网规模的致密气藏，可近似认为单井动态控制储量保持不变，根据当前产量制度下的生产数据，采用稳产时间预测模型计算气井在未来不同产量制度下的预测稳产时间。根据气田开发方案的设计自然稳产期，计算气井在不同配产量下的GpD(即自然稳产期末的稳产气量)，取GpD最大时的配产量作为目标配产量，从而实现产水气井的产量优化。

1.4 计算流程

对于致密气藏产水气井，首先根据井口生产数据，依次计算pwf，pr，G和C(qsc)，同时结合pwh-min计算pwf-min，进而计算pr-min，最后计算得到tF。计算流程见图1。其中，采用式(12)计算pwf，采用式(27)计算pr，采用式(26)计算G，采用式(28)计算C(qsc)，采用式(29)计算pwf-min，采用式(30)计算pr-min，采用式(36)计算tF。

图1 计算流程图Fig.1 Flow chart for calculation

2 模型验证

为验证模型的准确性，分别采用CMG 和Eclipse 建立数模案例。案例中，地层和流体的物性参数见表1，采用的相渗曲线见图2。CMG案例以3×104m3/d 的配产量进行生产，从2020-01-01稳产到2024-02-10，稳产时间为1 502 d；Eclipse案例以1.5×104m3/d 的配产量进行生产，从2020-01-01 稳产到2026-02-21，稳产时间为2 244 d；数模计算得到的井底流压和产水量分布见图3。

图2 气水相对渗透率曲线Fig.2 Relative permeability curves of gas and water

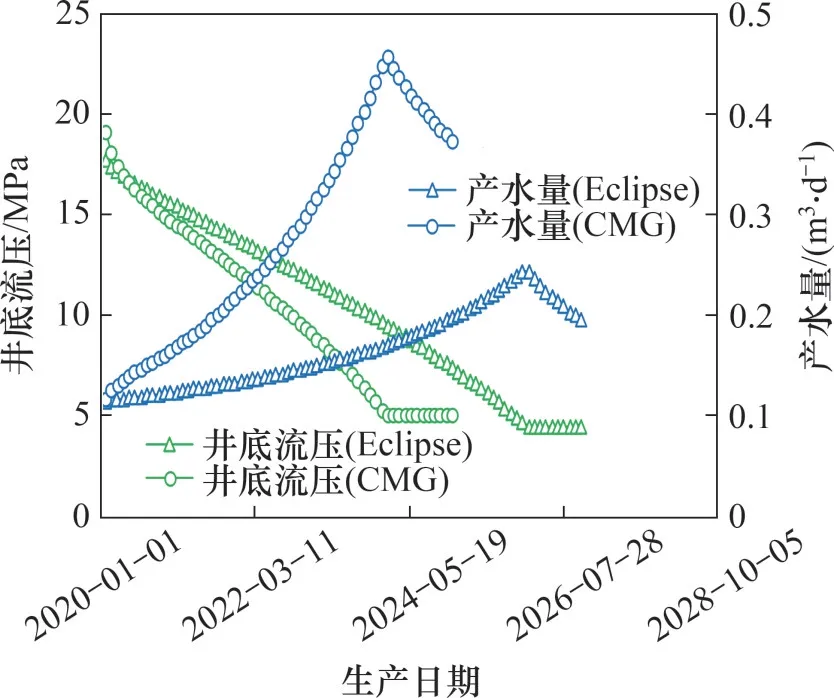
图3 井底流压和产水量变化特征Fig.3 Variation characteristics of bottomhole flowing pressure and water production

表1 地层和流体物性参数Table 1 Physical parameters of formation and fluid

选取2020-01-01到2020-12-31作为实际稳产时间，即tP=366 d，得到CMG案例的剩余稳产时间为1 135 d，Eclipse案例的剩余稳产时间为1 877 d。采用稳产时间预测模型，计算不同案例的预测稳产时间，其中Bwr采用经验公式[29]进行计算，得到tF(CMG)=1 197 d和tF(Eclipse)=1 953 d。

数值模拟结果显示，随着生产时间增加，自然稳产期内的产水量呈非线性增大，而本文模型在建立过程中，采用WP/tP的处理方式。为分析不同产水量处理方式对计算结果的影响，用自然稳产期内的实际平均产水量替换WP/tP，计算得到CMG 案例和Eclipse 案例中tF与实际稳产时间tP的相对误差分别为5.33%和3.98%，表明采用WP/tP的处理方式是可行的。

为进一步分析产水量对计算结果的影响以及模型的整体适用性，需选取不同的实际稳产时间进行计算，对不同案例进行对比，采用实际稳产时间占比作为分析指标，计算结果见图4。从图4可以看出：1)稳产初期，当实际稳产时间占比为10%时，CMG 案例和Eclipse 案例中tF与实际稳产时间tP的相对误差分别为12.57%和4.49%。2)随着实际稳产时间占比增大，相对误差随之减小；当实际稳产时间占比为50%时，CMG案例和Eclipse案例的稳产时间相对误差分别降至0.15% 和0.25%；当实际稳产时间占比继续增大时，稳产时间相对误差由正值转变为负值。3)稳产末期，当实际稳产时间占比为90%时，CMG案例和Eclipse案例中的tF与实际稳产时间tP相对误差分别为-10.30%和-5.22%。

图4 预测稳产时间tF与实际稳产时间tP的相对误差Fig.4 Relative error between tF and actual stable production time tP

随着实际稳产时间增加，模型的相对误差绝对值发生先减小后增大的变化，稳产初期和稳产末期的相对误差绝对值均较大，但产生原因却不相同。本文模型的建立基于气井已经进入拟稳态，且拟稳态阶段的生产压差为常数，而实际上，气井进入拟稳态需要时间，且数模的生产压差随着稳产时间增加而增大，并不严格遵循生产压差为常数这一近似条件。稳产初期，tF(CMG)=15 d，tF(Eclipse)=22 d，由于定产量生产时间较短，井底流压的下降速率还未趋于稳定，气井尚未真正进入拟稳态，导致相对误差绝对值较大。稳产末期，生产压差达到最大值，模型的相对误差绝对值亦达到拟稳态阶段的最大值。

CMG 案例在稳产末期的相对误差绝对值虽然达到10.30%，但此时的绝对误差仅为-16 d，仅占CMG 案例稳产时间的1.04%，从工程计算角度计算结果满足气藏开发实际需求。Eclipse 案例从稳产初期到稳产末期受到实际稳产时间的影响较小，其最大相对误差绝对值仅为5.22%，满足气藏开发实际需求。CMG和Eclipse的数模验证结果共同证明了本文模型的可靠性。

3 现场应用

鄂尔多斯盆地东南部某区块为典型的致密气藏，于2017年投入开发，随着生产进行，在现行产量制度下，部分气井无法满足设计自然稳产期要求，或者无法实现GpD最大的目标。A 井和B 井为该区块的两口典型产水气井，根据气田开发方案，A井和B井的设计自然稳产期均为8 a。A井自2017-04-11开始，以配产量4.0×104m3/d进行定产量生产，初期油压超过20 MPa，截至2019-04-30，油压下降到不足10 MPa，根据油压下降速率，初步估算A 井的剩余稳产时间仅剩1 a，无法达到开发方案的设计自然稳产期要求，亟需对A 井的产量制度进行优化。B 井自2017-04-10 开始，以配产量1.0×104m3/d 进行定产量生产，初期油压接近15 MPa，截至2019-03-30，油压仍超过13 MPa，根据油压下降速率，初步估算B 井的剩余稳产时间超过10 a，表明当前配产量未实现GpD最大这一目标，同时造成单井内部收益率较低，也应对B井的产量制度进行优化。

采用产水气井稳产时间预测模型，分别对A井和B井进行产量优化。相关计算参数如下：A井为直井，管柱内径为0.121 36 m，天然气相对密度为0.592，临界压力为4.73 MPa，临界温度为194.90 K，生产层位为本溪组，原始地层压力为26.22 MPa，原始偏差系数为0.959 6，地层温度为364.79 K，原始含水饱和度为0.3，井口最低外输压力为5.2 MPa；B 井为直井，管柱内径为0.121 36 m，天然气相对密度为0.585，临界压力为4.68 MPa，临界温度为192.74 K，生产层位为本溪组，原始地层压力为25.81 MPa，原始偏差系数为0.957 6，地层温度为361.98 K，原始含水饱和度为0.4，井口最低外输压力为5.2 MPa。

采取图1所示的计算流程，分别对A井和B井进行计算，得到不同配产量下设计自然稳产期末的稳产气量GpD见图5。从图5可知：随着配产量升高，GpD发生先增大后减小的变化。对于A 井，若以当前配产量4.0×104m3/d 继续生产，GpD仅为3 796.46×104m3；随着配产量降低，GpD增大，当配产量降低到1.5×104m3/d 时，GpD达到最大值5 547.02×104m3，故取1.5×104m3/d作为A井的目标配产量。对于B 井，若以当前配产量1.0×104m3/d继续生产，GpD仅为2 575.94×104m3；随着配产量升高，GpD增大，当配产量升高到2.0×104m3/d 时，GpD达到最大值4 495.94×104m3；故取2.0×104m3/d作为A井的目标配产量。

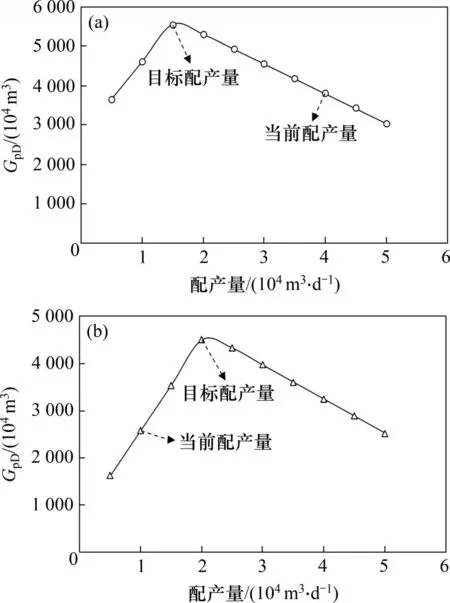
图5 配产量与设计自然稳产期末的稳产气量GpDFig.5 Production allocation and stable gas production at the end of designed natural stable production period

确定各自的目标配产量后，A井和B井分别于2019-05-01 和2019-03-31 对产量制度进行调整，然后继续生产，优化前后的产气量和产水量见图6，优化前后的油压见图7。优化后，截至2020-04-30，A 井的油压下降速率明显变小，根据油压下降速率，估算A 井的剩余稳产时间接近5 a，满足开发方案的设计自然稳产期要求；B井的油压下降速率加快，根据油压下降速率，估算B 井以2.0×104m3/d的配产量还能稳产5 a，在满足设计自然稳产期的同时，获得了更高的内部收益率。2口气井的产量优化效果显著，表明本文模型对于致密气井具有较强的实用性。

图6 优化前后的产气量和产水量Fig.6 Gas and water production before and after optimization

图7 优化前后的油压Fig.7 Wellhead tubing pressure before and after optimization

4 结论

1)采用逆向推演思路，从气液两相流井筒压力梯度方程出发，通过引入含水修正系数，推导了产水气井的井底流压解析模型；利用定容气驱产水气藏的物质平衡方程，结合拟稳态阶段地层压力的变化规律，建立了产水气井的平均地层压力计算模型；最后以井口最低外输压力为约束条件，建立了产水气井的稳产时间预测模型，实现了“井口—井底—产层”的一体化计算，丰富了致密气藏有效开发关键技术体系。

2)随着实际稳产时间增加，模型的预测稳产时间与实际稳产时间之间的相对误差绝对值先减小后增大；CMG 案例在稳产末期的稳产时间相对误差绝对值较大，但绝对误差很小；Eclipse 案例的稳产时间最大相对误差绝对值仅为5.22%；CMG案例和Eclipse案例的预测稳产时间与实际验证结果，证明了稳产时间预测模型的准确性和适用性。

3)将稳产时间预测模型应用于产水气井的产量优化，优化后的气井生产动态显示，A井能够满足开发方案的设计要求，B井能够获得更高的内部收益率，优化效果显著，表明本文模型对于致密气井具有较强的实用性，能够有效提升气田开发管理水平。