不同地应力状态下各向异性地层斜井井壁破裂规律

马天寿，王浩男，杨赟，彭念，刘阳

(1.西南石油大学油气藏地质及开发工程国家重点实验室，四川成都，610500；2.中国石油川庆钻探工程有限公司钻采工程技术研究院，陕西西安，710021)

井壁破裂压力是石油与天然气钻井与水力压裂的关键参数[1-2]。在钻井过程中，井壁破裂压力与井漏密切相关，井漏的主要原因是井壁被压裂；为了避免发生井漏，井壁破裂压力通常被当作井筒压力的上限值，因此，井壁破裂压力是进行钻井工程设计、钻井液密度优化与钻井施工措施制定的重要依据。准确预测井壁破裂压力并优化钻井措施，可以有效避免由于地层破裂而诱发产生的井漏、井喷、井壁垮塌、卡钻等井下复杂和事故[3-5]。而水力压裂过程中，为了在井眼周围形成裂缝、提高储层有效渗透率，必须压裂井壁形成裂缝，这就要求井筒压力达到甚至超过井壁破裂压力，因此，井壁破裂压力是进行水力压裂设计、压裂设备选型与压裂施工措施制定的重要依据[6-8]。由此可见，井壁破裂压力在不同作业环节中具有不同的作用和意义。

井壁破裂压力的预测是井壁稳定分析的重要方面，是比较经典的岩石力学问题。对于任意斜井情况下井壁破裂压力的预测，国内外开展了大量的研究。1979年，BRADLEY[9]建立了斜井井周应力分布模型，研究了斜井井壁稳定性，实现了对任意斜井井壁起裂压力的计算。黄荣樽等[10-13]采用类似方法预测了任意斜井井壁破裂压力，并研究了井壁裂缝起裂位置及其走向。这类方法假设井壁岩石是各向同性连续介质，这对于浅部地层井壁稳定研究来说是合理的[14-17]，多年的实践也证实该方法具有较高的精度，但是，对于埋藏较深、地质构造作用强烈的沉积岩地层，均存在一定程度的各向异性，各向同性假设已经不能满足实际工程需求[18-19]。为此，国内外学者研究了各向异性对井壁稳定的影响。在国外，AADNOY 等[20-21]基于各向异性介质平面孔口问题解法，建立了各向异性介质井壁稳定力学模型，并研究了井壁应力分布和井壁稳定性，结果显示各向异性对破裂压力影响显著，对坍塌压力影响相对较低。ONG等[22-23]采用类似方法分析了任意斜井各向异性地层井壁稳定性，重点分析了各向异性程度、地应力及井眼轨迹的影响。ONG 等[24]还专门研究了各向异性、井眼轨迹和典型产状下井壁破裂压力变化规律。在国内，崔杰等[25-26]研究了特定产状下横观各向同性地层任意斜井井壁应力分布规律及井壁稳定性，主要研究了井壁坍塌压力变化规律；马天寿等[27-28]研究了弹性各向异性地层中，各向异性对直井破裂压力的影响规律，并进一步考虑了抗张强度各向异性的影响；MA等[29]综合弹性和强度各向异性影响，建立了水平井的井壁破裂压力预测模型。

由此可见，国内外针对各向异性介质中斜井井壁稳定性开展了大量研究，大多数研究主要集中于各向异性对井壁应力的影响[20-26]，部分学者对特定产状下直井、水平井等典型井破裂压力进行了研究[20-24,27-29]，也证实了地层各向异性对井壁破裂压力的显著影响，但对于不同地应力状态、地层产状、井眼轨迹的综合影响研究并不充分，尤其是各向异性地层中多种因素影响的井壁裂缝起裂机制和规律尚不完全明确。为此，本文作者在分析岩石各向异性弹性力学特性的基础上，建立考虑各向异性的斜井井壁破裂压力预测模型，分析典型地应力状态下不同井眼轨迹、产状和各向异性对井壁破裂压力的影响规律，以揭示各向异性地层中斜井井壁破裂的力学机制，以便为各向异性地层斜井钻井、压裂设计与施工提供理论依据。

1 各向异性地层斜井破裂压力模型

1.1 各向异性岩石弹性特征

各向异性地层岩石通常发育有大量层理等软弱结构面，导致其表现出显著的各向异性特征[30]。图1所示为典型岩石的弹性各向异性特征实测结果[31]，其中，图1(a)所示为平行和垂直于层理方向弹性模量交会图，图1(b)所示为平行和垂直于层理方向泊松比交会图。图1中彩色色标标示的数字1～10代表不同类型的岩石，其中，1为Baxter页岩实测静态弹性参数，2为Baxter页岩实测动态弹性参数，3 为多种非常规页岩实测静态弹性参数，4 为Devonian页岩实测动态弹性参数，5为卤水饱和页岩的实测动态弹性参数，6 为Jurassic 页岩的实测动态弹性参数，7为Kimmeridge页岩的实测动态弹性参数，8为Cretaceous页岩的实测动态弹性参数，9 为Bakken 页岩的实测动态弹性参数，10 为Woodford 页岩的实测动态弹性参数。由图1可知：垂直于层理方向的弹性模量明显低于平行层理方向的弹性模量，垂直与平行方向弹性模量的比值(E'/E)介于0.2～1.5，且主要分布在0.5～1.0之间；垂直与平行层理方向的泊松比无显著规律，垂直与平行方向泊松比的比值(v'/v)介于0.2～6.7，且主要分布在0.5～2.0 之间。无论是弹性模量还是泊松比均存在较为显著的各向异性，弹性各向异性将显著影响井周应力分布，因此，在井壁破裂压力预测时，有必要考虑弹性各向异性的影响。

图1 典型岩石垂直和平行方向弹性参数交会图(修改自文献[31])Fig.1 Cross-plot of elastic parameters between parallel and perpendicular direction for typical rocks(modified from Ref.[31])

1.2 斜井井周应力分布

对于各向异性地层介质中的任意倾斜井眼(如图2所示)，井周应力分布模型涉及5 个坐标及其转换[32]：

图2 各向异性地层斜井坐标转换关系[32]Fig.2 Coordinate transformation of inclined well in the anisotropic formation[32]

1)整体坐标(x，y，z)，也称大地坐标(NEZ)；

2)地应力局部坐标(xs，ys，zs)，最大水平地应力与北坐标夹角为βs；

3)井眼局部坐标(xb，yb，zb)，井眼轴线的井斜角为αb，方位角为βb；

4)圆柱坐标(rb，θb，zb)；

5)地层局部坐标(xw，yw，zw)，地层中层理面的倾角为αw，倾向为βw。

为了建立模型，进行如下假设条件：将岩石视为均匀连续的横观各向同性介质，岩石变形满足弹性变形及小变形假设，井周应力应变满足广义平面应变假设，并忽略渗流、温度和钻井液化学作用的影响。

对于横观各向同性弹性介质，地层局部坐标(xw，yw，zw)下的岩石本构方程表示为

其中：

[A]为地层局部坐标(xw，yw，zw)下的岩石柔度矩阵；G'为横观各向同性地层岩石的剪切模量；{σw} 和{εw}(xw，yw，zw)的应力和应变，{ε}w={εxx，εyy，εzz，2γxy，2γxz，2γyz}T，{σ}w={σxx，σyy，σzz，τxy，τxz，τyz}T。

结合图2中的坐标转换关系，利用BOND变换关系，可得井眼局部坐标(xb，yb，zb)下地层的柔度矩阵：

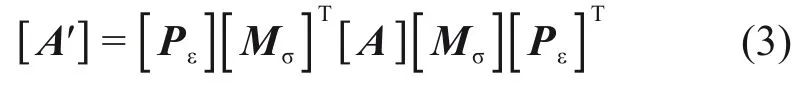
式中：[A′]为井眼局部坐标(xb，yb，zb)下岩石的柔度矩阵；[Pε]为井眼局部坐标(xb，yb，zb)与整体坐标(x，y，z)之间的应变转换BOND 矩阵；[Mσ]为地层局部坐标(xw，yw，zw)与整体坐标(x，y，z)之间的应力转换BOND矩阵。

井周围岩受原地应力、井筒压力和井眼形成的影响，井周应力分布可分为3个分量：井眼钻开前作用的原地应力分量、井眼形成所引起的应力分量、井壁流体压力引起的应力分量。于是，利用各向异性介质平面孔口问题的应力解法，将上述3种应力分量进行线性叠加后，可得斜井井周应力分布解析解[23-26]：

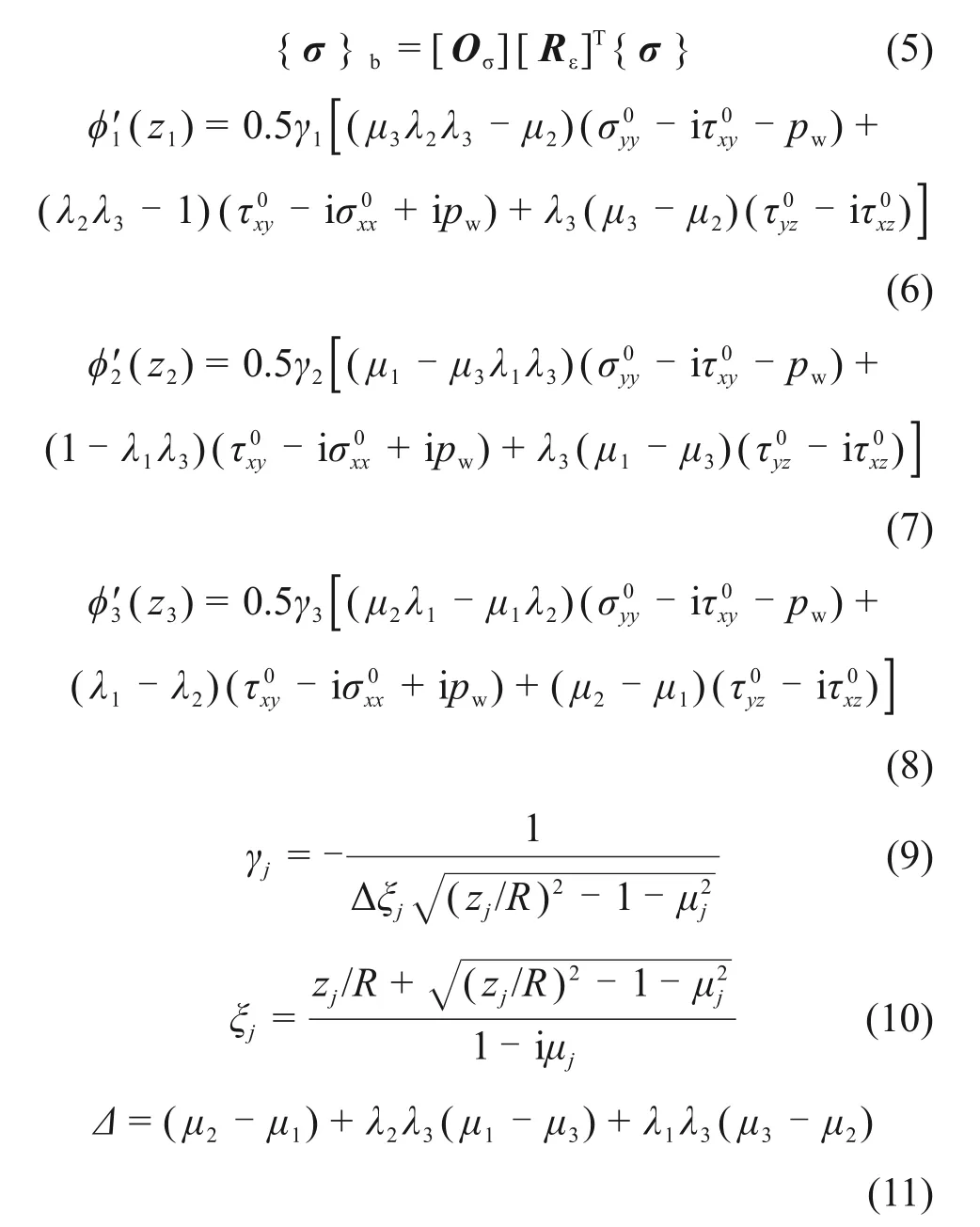
式中：{σ}b为井眼局部坐标(xb，yb，zb)下的应力，{σ}s为地应力局部坐标(xs，ys，zs)下的应力矢量，{σ}s={σv，σH，σh，0，0，0}T；σv，σH和σh分别为垂向应力、水平最大地应力和水平最小地应力；[Rε]为地应力局部坐标(xs，ys，zs)与整体坐标(x，y，z)之间的应力转换BOND 矩阵；[Oσ]为井眼局部坐标(xb，yb，zb)与整体坐标(x，y，z)之间的应力转换BOND矩阵；aij为井眼局部坐标(xb，yb，zb)下地层的柔度矩阵系数；φ′1(z1)，φ′2(z2)和φ′3(z3)为解析函数；μj为与应变协调方程对应的特征方程特征根，根据柔度矩阵系数计算；λj，γj，ξj和Δ为与特征根有关的中间计算量；pw为井筒压力；i 为虚数单位；Re 表示实部；zj为复数；j=1，2，3。

1.3 破裂压力计算模型

井壁破裂是井壁张应力超过岩石强度所致。为了求解斜井井壁破裂压力，必须先求解井壁主应力特别是最小主应力。为此，先计算出井眼圆柱坐标下应力分量，根据图2所示的坐标关系，通过转轴公式变换，可得井眼圆柱坐标下的井壁应力[26]：

井壁岩石单元受力分析如图3所示。井壁径向应力为主应力，因此，与井壁径向应力垂直的井壁θ-zb平面为主应力面，井壁破裂取决于井壁θ-zb平面的最小主应力。

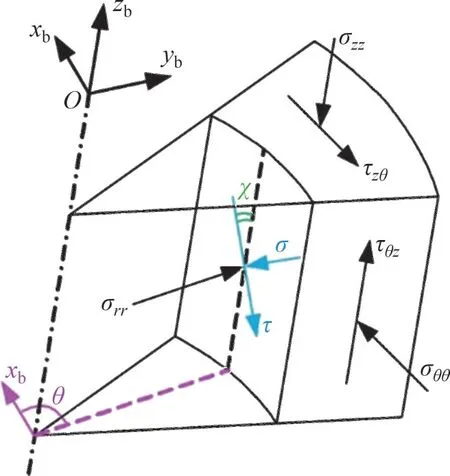
图3 井壁岩石单元的受力分析[14]Fig.3 Stress analysis of rock element on wall of borehole[14]

为了便于进行井壁破裂的判断及其位置的计算，必须先求出θ-zb平面的最小主应力。根据应力分析，与zb轴呈角度χ的斜平面上的正应力σ和剪应力τ与式(12)中各应力分量间的关系为[14]

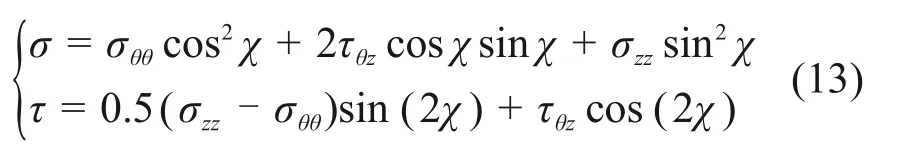
为了求出井壁最小主应力，将式(13)中的正应力对χ进行求导，并令

可得正应力极值所对应的χ：

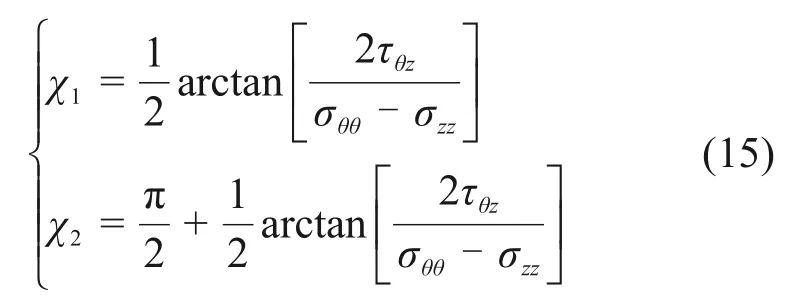
将χ1和χ2代入式(14)，即可求得井壁θ-zb平面的2个主应力：

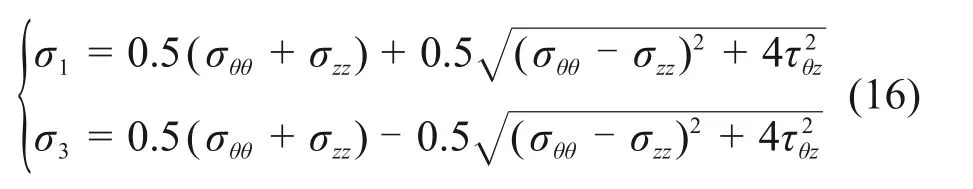
由于井壁破裂是井壁最小主应力(拉应力)超过岩石拉伸强度所致，即拉伸破坏取决于地层岩石的抗张强度St，若同时考虑Biot有效应力，则拉伸破坏准则可写为

式中：σ3为井壁最小主应力；St为岩石抗张强度；α为Biot系数；pp为孔隙压力。

联立式(4)，(12)，(16)和(17)，求解式(17)即可得到井壁起裂时对应的破裂压力临界值。需要注意的是，在弹性参数、地应力、孔隙压力、岩石强度已知条件下，给定井斜和方位的斜井井壁最小主应力与井周角有关，也就是说，不同井周角的破裂压力临界值不同，而实际取值为不同井周角下的最低破裂压力临界值。

2 不同地应力状态下破裂压力预测

为了分析不同地应力状态下各向异性地层斜井井壁破裂压力，准确认识各向异性地层斜井井壁起裂规律和机理，以川南地区深层页岩气区块龙马溪页岩储层为例进行计算和分析。川南地区深层龙马溪页岩储层基础参数如下：垂深为3 800 m，井眼直径为215.9 mm，孔隙压力梯度为1.95 g/cm3，Biot 系数为0.8，平行于层理方向弹性模量为37.8 GPa，垂直于层理方向弹性模量为18.6 GPa，平行于层理方向泊松比为0.20，垂直于层理方向泊松比为0.25，页岩抗张强度为6.0 MPa，层理倾角为10°，层理倾斜方位为105°，典型的地应力状态如表1所示。为便于后续分析各向异性影响，定义弹性各向异性系数：弹性模量各向异性系数nE=E/E'，泊松比各向异性系数nv=v'/v。

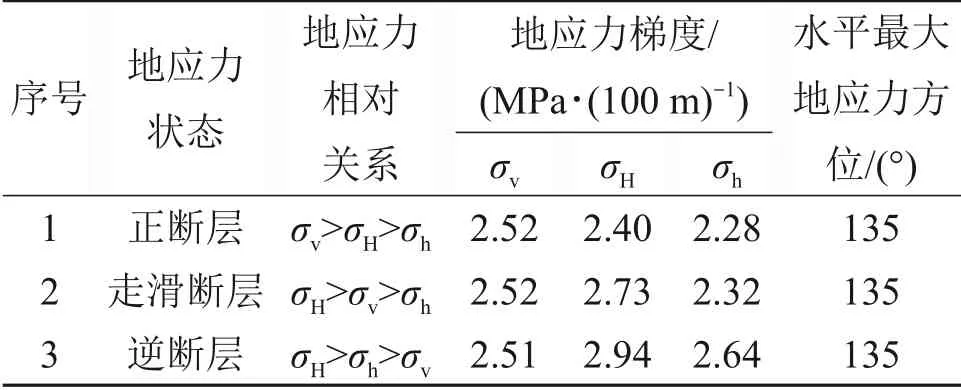
表1 川南深层页岩储层典型地应力状态表Table 1 Typical in-situ stress states of deep shale reservoir in the southern Sichuan

2.1 正断层应力状态

2.1.1 井眼轨迹的影响

井眼轨迹对破裂压力影响显著，为了分析和对比不同井眼轨迹下各向同性与各向异性之间的差异，计算正断层应力状态下各向同性和各向异性井壁破裂压力当量密度分布规律，结果如图4所示。为了直观展示井眼轨迹对井壁破裂压力当量密度的影响，采用下半球投影图表达计算结果。图4中同心圆代表不同倾角，径向射线代表不同倾斜方位，而破裂压力用当量密度的形式以云图显示。图4(a)所示为各向同性模型破裂压力当量密度(ρfISO)计算结果，图4(b)所示为各向异性模型破裂压力当量密度(ρfTVI)计算结果，图4(c)所示为各向同性模型与各向异性模型计算破裂压力当量密度差值(ρfISO-ρfTVI)。由图4可知：1)对于各向同性和各向异性模型计算结果，破裂压力随井斜、方位的变化规律基本一致，即沿最大水平地应力方向的破裂压力当量密度最低，而沿最小水平地应力方向的破裂压力当量密度相对较高，直井的破裂压力当量密度介于二者之间。沿最小水平地应力方向钻进斜井和水平井破裂压力较高，有利于钻井井漏的预防，尽管破裂压力高不利于水力压裂，但有利于形成垂直于井眼轴线的垂直裂缝，有利于提升压裂改造增产效果。因此，推荐沿最小水平地应力方向钻进斜井和水平井，若破裂压力过高，则可适当偏离最小水平地应力方向一定角度。2)各向同性模型计算的破裂压力当量密度介于3.01～3.45 g/cm3，而各向异性模型计算的破裂压力当量密度介于2.91～3.45 g/cm3；与各向同性模型计算结果相比，考虑各向异性影响后，破裂压力当量密度整体上呈下降趋势，其中，井斜小于45°时降幅较小，井斜大于60°时降幅变大，且随井斜角增加而增大，沿最大水平地应力方向的水平井破裂压力当量密度降低最多，其最大降幅及其比例分别为0.10 g/cm3和3.32%。

图4 正断层应力状态下破裂压力当量密度下半球投影图Fig.4 Hemispherical projection of equivalent density of fracture pressure under normal faulting state

2.1.2 层理产状和各向异性的影响

以最小水平地应力方向(45°)水平井为例，计算不同产状和各向异性条件下的破裂压力，结果如图5所示，为了直观展示层理产状对井壁破裂压力的影响，采用下半球投影图表达计算结果，图5中同心圆代表不同层理倾角，径向射线代表不同层理倾斜方位，而破裂压力用当量密度的形式以云图显示。各向同性计算的该井破裂压力当量密度为3.37 g/cm3。图5(a)所示为中等各向异性(nE=2.0，nv=1.25)条件下的破裂压力当量密度计算结果，图5(b)所示为中等各向异性条件下的破裂压力当量密度差值(ρfISO-ρfTVI)，图5(c)所示为强各向异性(nE=4.0，nv=2.5)条件下的破裂压力当量密度计算结果，图5(d)所示为强各向异性条件下的破裂压力当量密度差值(ρfISO-ρfTVI)。从图5可知：1)在各向异性系数相同的情况下，层理产状对破裂压力影响较显著；整体上，低角度层理将导致破裂压力当量密度降低，不利于井漏的预防，却有利于水力压裂；倾向沿着最大水平地应力方向(135°)的高角度层理将导致破裂压力当量密度增加，有利于井漏的预防，却不利于水力压裂；倾向沿着最小水平地应力方向(45°)的中高角度层理影响较小。2)对于破裂压力当量密度降低的情形，在中等各向异性条件下，破裂压力当量密度可降低至3.32 g/cm3，其最大降幅及其比例分别为0.05 g/cm3和1.48%；在强各向异性条件下，破裂压力当量密度可降低至3.25 g/cm3，其最大降幅及其比例分别为0.12 g/cm3和3.56%。3)对于破裂压力当量密度增加的情形，在中等各向异性条件下，破裂压力当量密度可增加至3.40 g/cm3，其最大增幅及其比例分别为0.03 g/cm3和0.89%；在强各向异性条件下，破裂压力当量密度可增加至3.43 g/cm3，其最大增幅及其比例分别为0.06 g/cm3和1.78%。

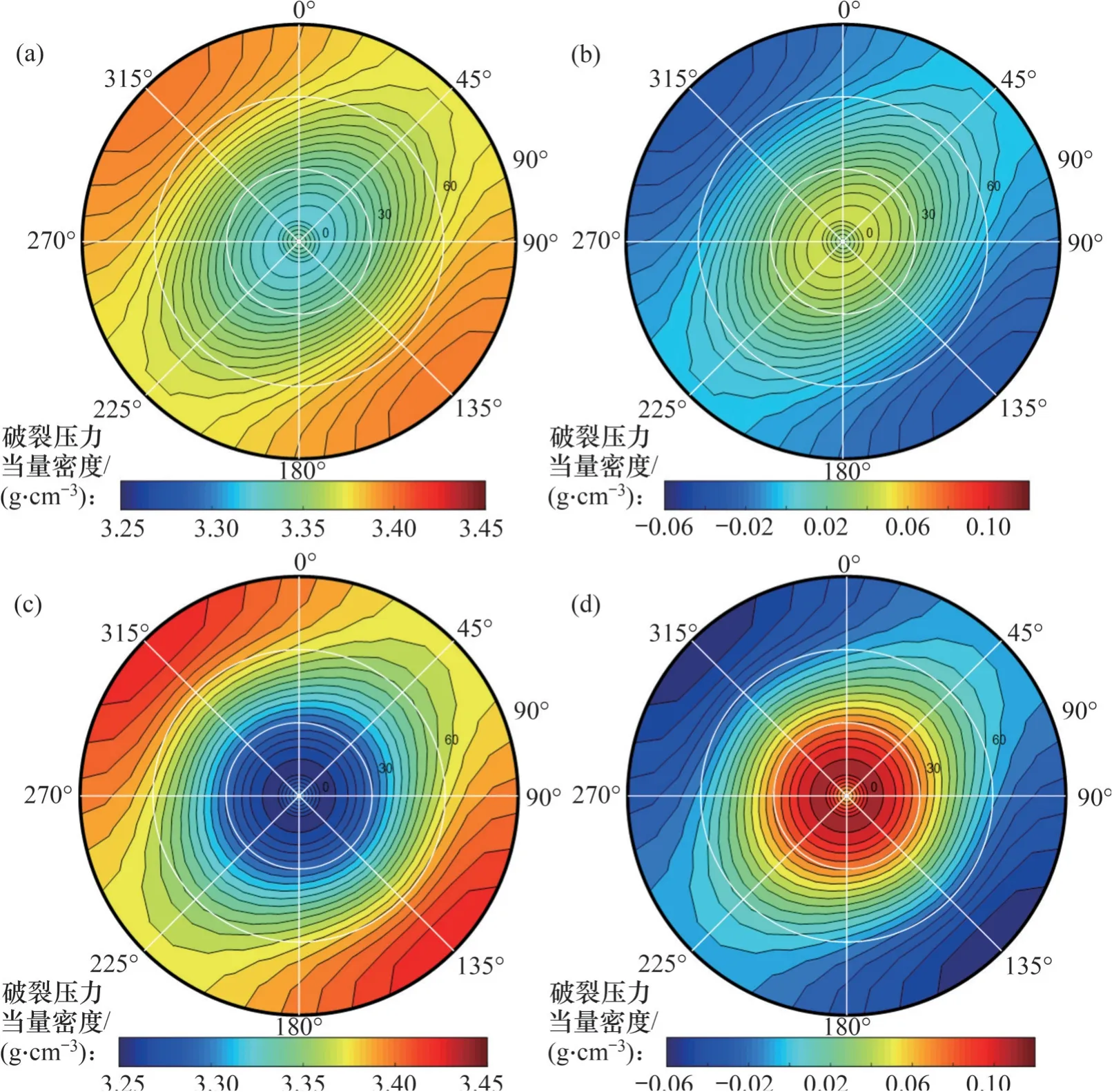
图5 正断层应力状态下层理产状和各向异性对破裂压力当量密度的影响Fig.5 Influence of bedding occurrence and anisotropy on equivalent density of fracture pressure under normal faulting state

2.2 走滑断层应力状态

2.2.1 井眼轨迹的影响

为了分析不同井眼轨迹对井壁破裂的影响，并对比各向同性与各向异性之间的差异，计算走滑断层应力状态下任意斜井井壁破裂压力当量密度分布规律，结果如图6所示，类似地，采用下半球投影图表达计算结果。图6(a)所示为各向同性模型破裂压力当量密度(ρfISO)计算结果，图6(b)所示为各向异性模型破裂压力当量密度(ρfTVI)计算结果，图6(c)所示为各向同性与各向异性模型计算的破裂压力当量密度差值(ρfISO-ρfTVI)。由图6可知：1)对于各向同性和各向异性模型，破裂压力当量密度随井斜、方位的变化规律基本一致，即随着井斜角增加，破裂压力当量密度逐渐增加，沿最大水平地应力方向的破裂压力当量密度较低，沿最小水平地应力方向的破裂压力当量密度相对较高，偏离最小水平地应力约30°方向的破裂压力当量密度最高。沿最小水平地应力方向钻进斜井和水平井破裂压力当量密度较高，有利于钻井井漏的预防。尽管高破裂压力不利于水力压裂，但有利于形成垂直于井眼轴线的垂直裂缝，有利于提升压裂改造增产效果。因此，推荐沿最小水平地应力方向钻进斜井和水平井。2)各向同性模型计算的破裂压力当量密度介于2.93～3.67 g/cm3，而各向异性模型计算的破裂压力当量密度介于2.92～3.67 g/cm3；与各向同性模型计算结果相比，考虑各向异性影响后，破裂压力当量密度整体上呈下降趋势，其中，对偏离最小水平地应力方向45°以内的斜井、水平井以及直井基本没有影响，对偏离最大水平地应力方向45°以内的斜井和水平井具有较明显的影响，破裂压力当量密度最大降幅及其比例分别为0.09 g/cm3和3.00%。

图6 走滑断层应力下破裂压力当量密度下半球投影图Fig.6 Hemispherical projection of equivalent density of fracture pressure under strike-slip faulting state

2.2.2 层理产状和各向异性的影响

类似地，以最小水平地应力方向(45°)水平井为例，计算不同产状和各向异性条件下的破裂压力，结果如图7所示，类似地，采用下半球投影图表达计算结果，其中，各向同性计算的该井破裂压力当量密度为3.52 g/cm3。图7(a)所示为中等各向异性(nE=2.0，nv=1.25)条件下的破裂压力当量密度计算结果，图7(b)所示为中等各向异性条件下的破裂压力当量密度差值(ρfISO-ρfTVI)；图7(c)所示为强各向异性(nE=4.0，nv=2.5)条件下的破裂压力当量密度计算结果，图7(d)所示为强各向异性条件下的破裂压力当量密度差值(ρfISO-ρfTVI)。从图7可知：1)在各向异性系数相同的情况下，层理产状对破裂压力影响也较为显著，整体上变化规律与正断层应力的变化规律相反，低角度层理将导致破裂压力当量密度增加，有利于井漏的预防，却不利于水力压裂；倾向沿着最大水平地应力方向(135°)的高角度层理将导致破裂压力当量密度降低，不利于井漏的预防，却有利于水力压裂；倾向沿着最小水平地应力方向(45°)的中高角度层理影响较小。2)对于破裂压力降低的情形，在中等各向异性条件下，破裂压力当量密度可降低至3.44 g/cm3，其最大降幅及其比例分别为0.08 g/cm3和2.27%；在强各向异性条件下，破裂压力当量密度可降低至3.31 g/cm3，其最大降幅及其比例分别为0.21 g/cm3和5.97%。3)对于破裂压力增加的情形，在中等各向异性条件下，破裂压力当量密度可增加至3.67 g/cm3，其最大增幅及其比例分别为0.15 g/cm3和4.26%；在强各向异性条件下，破裂压力当量密度可增加至3.10 g/cm3，其最大增幅及其比例分别为0.10 g/cm3和2.84%。

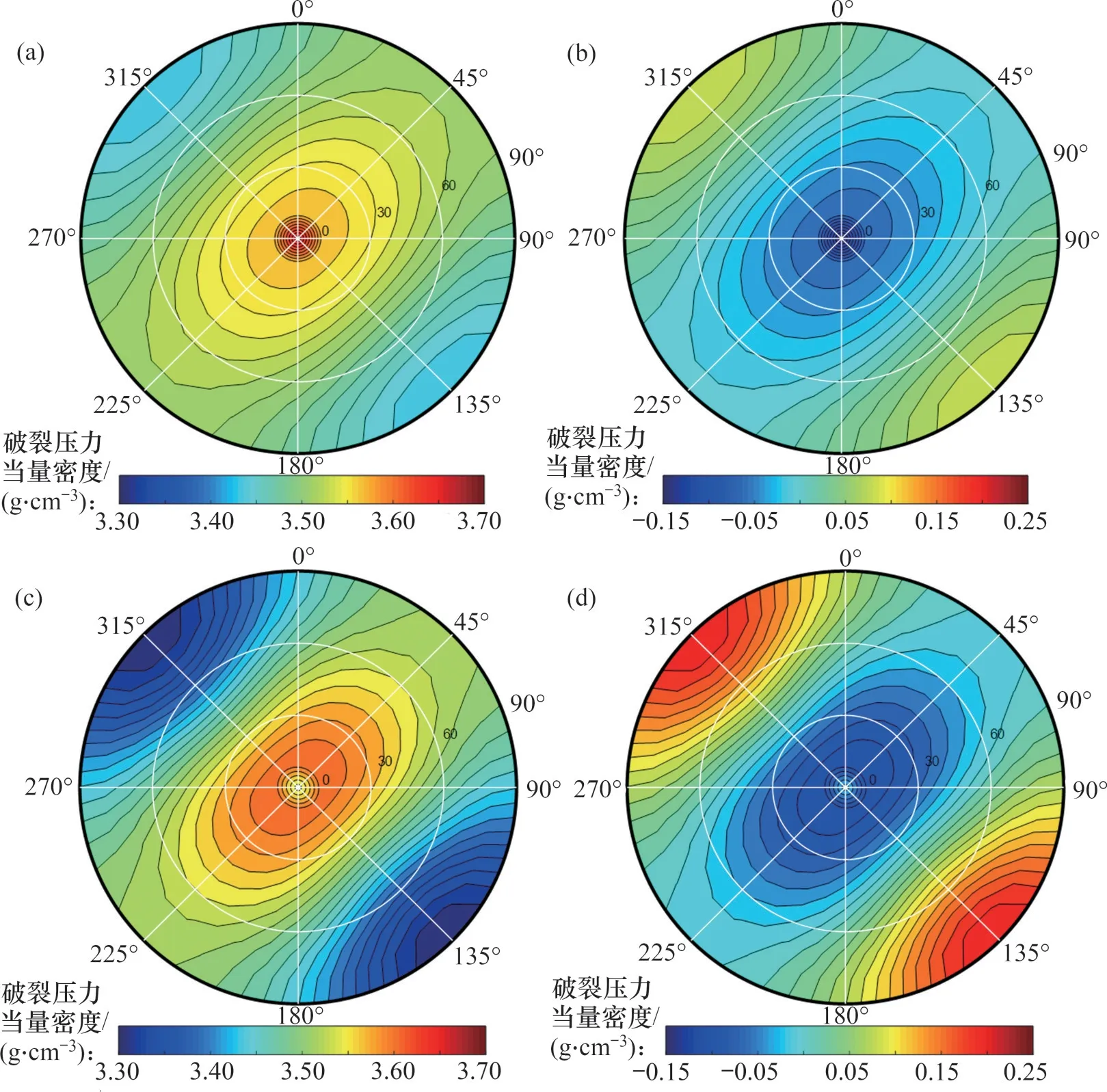
图7 走滑断层应力状态下层理产状和各向异性对破裂压力当量密度的影响Fig.7 Influence of bedding occurrence and anisotropy on equivalent density of fracture pressure under strike-slip faulting state

2.3 逆断层应力状态

2.3.1 井眼轨迹的影响

为了分析不同井眼轨迹对井壁破裂的影响，并对比各向同性与各向异性之间的差异，计算逆断层应力状态下任意斜井井壁破裂压力当量密度分布规律，结果如图8所示，类似地，采用下半球投影图表达计算结果。图8(a)所示为各向同性模型破裂压力当量密度(ρfISO)计算结果，图8(b)所示为各向异性模型破裂压力当量密度(ρfTVI)计算结果，图8(c)所示为各向同性与各向异性模型计算的破裂压力当量密度差值(ρfISO-ρfTVI)。由图8可知：1)对于各向同性和各向异性模型，破裂压力当量密度随井斜、方位的变化规律基本一致，沿最大水平地应力方向的破裂压力当量密度较高，沿最小水平地应力方向的破裂压力当量密度相对较低，直井的破裂压力当量密度介于二者之间，而沿最大水平地应力方向40°～50°的斜井破裂压力当量密度最高。沿最小水平地应力方向钻进斜井和水平井破裂压力当量密度较低，这并不利于钻井井漏的预防，但有利于水力压裂，而且有利于形成垂直于井眼轴线的垂直裂缝，从而提升压裂改造增产效果。因此，推荐沿最小水平地应力方向钻进斜井和水平井。2)各向同性模型计算的破裂压力当量密度介于3.29～3.89 g/cm3，而各向异性模型计算的破裂压力当量密度介于3.39～3.90 g/cm3；与各向同性模型计算结果相比，考虑各向异性影响后，破裂压力当量密度整体上呈上升趋势、中低角度的斜井存在破裂压力当量密度降低的现象，其中，沿最大水平地应力方向且井斜介于10°～50°的斜井破裂压力当量密度略有降低，破裂压力当量密度最大降幅及其比例分别为0.04 g/cm3和1.03%，而直井、沿最小水平地应力方向且井斜大于50°的大斜度井和水平井破裂压力当量密度显著增加，破裂压力当量密度最大增幅及其比例分别为0.11 g/cm3和3.34%。

图8 逆断层应力状态下破裂压力当量密度下半球投影图Fig.8 Hemispherical projection of equivalent density of fracture pressure under reverse faulting state

2.3.2 层理产状和各向异性的影响

以最小水平地应力方向(45°)水平井为例，计算不同产状和各向异性条件下的破裂压力当量密度，结果如图9所示，类似地，采用下半球投影图表达计算结果，其中，各向同性计算的该井破裂压力当量密度为3.27 g/cm3。图9(a)所示为中等各向异性(nE=2.0，nv=1.25)条件下的破裂压力当量密度计算结果，图9(b)所示为中等各向异性条件下的破裂压力当量密度差值(ρfISO-ρfTVI)；图9(c)所示为强各向异性(nE=4.0，nv=2.5)条件下的破裂压力当量密度计算结果，图9(d)所示为强各向异性条件下的破裂压力当量密度差值(ρfISO-ρfTVI)。从图9可知：

图9 逆断层下层理产状和各向异性对破裂压力当量密度的影响Fig.9 Influence of bedding occurrence and anisotropy on equivalent density of fracture pressure under reverse faulting state

1)在各向异性系数相同的情况下，层理产状对破裂压力当量密度影响较大；整体上其变化规律与正断层应力变化规律相反，与走滑断层应力变化规律相似，低角度层理将导致破裂压力当量密度增加，有利于井漏的预防，却不利于水力压裂；倾向沿着最大水平地应力方向(135°)的高角度层理将导致破裂压力当量密度降低，不利于井漏的预防，却有利于水力压裂；倾向沿着最小水平地应力方向(45°)的中高角度层理影响较小。

2)对于破裂压力降低的情形，在中等各向异性条件下，破裂压力当量密度可降低至3.10 g/cm3，其最大降幅及其比例分别为0.17 g/cm3和5.20%；在强各向异性条件下，破裂压力当量密度可降低至2.84 g/cm3，其最大降幅及其比例分别为0.43 g/cm3和13.15%。

3)对于破裂压力增加的情形，在中等各向异性条件下，破裂压力当量密度可增加至3.51 g/cm3，其最大增幅及其比例分别为0.24 g/cm3和7.34%；在强各向异性条件下，破裂压力当量密度可增加至3.55 g/cm3，其最大增幅及其比例分别为0.28 g/cm3和8.56%。

4)与正断层和走滑断层应力状态的计算结果相比，逆断层应力状态下层理产状对破裂压力的影响更大。

3 结论

1)在正断层和走滑断层应力状态下，沿最大水平地应力方向的破裂压力最低，而沿最小水平地应力方向的破裂压力相对较高；在逆断层应力状态下，沿最大水平地应力方向的破裂压力较高，沿最小水平地应力方向的破裂压力相对较低。

2)与各向同性模型计算结果相比，在正断层和走滑断层应力状态下，考虑各向异性影响后，破裂压力当量密度整体上都呈下降趋势。其中，正断层应力状态下破裂压力当量密度降幅及其比例分别可达0.10 g/cm3和3.32%，在走滑断层应力状态下，破裂压力当量密度降幅及其比例分别可达0.09 g/cm3和3.00%。在逆断层应力状态下，与各向同性模型计算结果相比，考虑各向异性影响后破裂压力当量密度整体上呈上升趋势，破裂压力当量密度增幅及其比例分别可达0.11 g/cm3和3.34%。

3)在各向异性系数相同的情况下，层理产状对破裂压力当量密度影响较为显著。在正断层应力状态下，整体上低角度层理将导致破裂压力当量密度降低，而倾向沿着最大水平地应力方向(135°)的高角度层理将导致破裂压力当量密度增加；在走滑断层和逆断层应力状态下，低角度层理都将导致破裂压力当量密度增加，而倾向沿着最大水平地应力方向(135°)的高角度层理将导致破裂压力当量密度降低。

4)随着页岩弹性各向异性程度的增加，水平井破裂压力当量密度变化越大，且逆断层应力状态下破裂压力变化最为显著；在强各向异性条件下，逆断层应力状态破裂压力当量密度降幅及其比例分别可达0.43 g/cm3和13.15%、增幅及其比例分别可达0.28 g/cm3和8.56%。