近海欠密实砂质海床内波致渐进液化特征研究
王良民,叶剑红,朱长歧
(中国科学院武汉岩土力学研究所 岩土力学与工程国家重点实验室,湖北 武汉 430071)
1 引 言
我国拥有300×104km2海域,1.8×104km 的海岸线,是海洋大国。近20 多年来,我国对海洋资源的开发和利用逐渐起步和发展,在近海海域建设了大量的海洋结构物,如军事港口防波堤、近海风力发电机、海底管线、采油平台等。然而,近海海洋结构物由于受到海洋波浪环境荷载的无休止作用,它们的稳定性问题比陆地结构物要复杂很多;尤其是建于第四纪欠密实海床地基上的海洋结构物,在风浪作用下的稳定性非常差。据国土资源部历年发布的海洋灾害公布统计显示,我国每年因热带风暴在东部沿海登陆,造成约40 km 防波堤毁坏;风暴后常有海底输油、气管线断裂事故发生。
通过大量的试验和现场调查发现,海洋结构物的破坏机制大概有3 种类型:①过大的冲击力导致结构物被推倒;②结构物在长时间循环波浪荷载作用下发生渐进式永久水平位移;③结构物海床地基发生波致液化而失去承载力。其中第③种类型是最常发生,但经常被忽视。波浪作用下海床地基发生液化存在两种机制:瞬态液化和累积液化。目前,关于瞬态液化的研究已经比较充分,它一般只能发生在非常密实的弹性海床中,并且只能存在于波谷的下方,随着波浪的作用,短时间出现,又短时间内消失,这种机制的液化深度一般不会很深,这方面的经典成果见文献[1-5]。然而,近海环境中,非常密实的海床土是很少见的,第四纪新近沉积的欠密实的沉积物大范围分布,在波浪的持续作用下,欠密实的海床内超孔隙压力逐渐累积(由于发生了不可恢复到体积塑性变形),使粒间接触有效应力逐渐减小,最终发生累积液化。该类型的液化一旦发生,海床土基本丧失承载能力,建于其上的海洋结构物将发生失稳破坏。
在最近10 多年对于波浪作用下欠密实海床地基的液化问题的研究才受到重视[6-9]。对松砂海床地基内的波浪导致液化的认识还不够深入,尤其缺乏对这种液化的属性和过程定量上的分析。其结果就是对新建的海洋结构物的海床地基的稳定性没有足够地把握,导致结构物倾倒或者垮塌。其中一个典型的例子是我国2013年刚刚建成的南海某军事港口深水防波堤,在超级台风蝴蝶登陆时发生大面积毁坏,造成极大的损失。目前,我国在南海珊瑚岛礁近海存在着大量的防波堤工程建设,这些工程结构物的吹填钙质砂地基在太平洋热带风暴侵袭下的稳定性极为重要;因此,定量研究欠密实海床土在波浪作用下的液化特征具有重要意义。本文采用经广泛验证的数值耦合模型FSSI-CAS 2D为计算工具,定量研究欠密实海床地基在波浪作用下,其内部的液化特征和动态过程,以增强对波导致液化性质的认识。
2 数值计算模型简介
针对波浪、地震荷载作用下海洋结构物及其海床地基的动力反应问题,在前人研究的基础上,Ye[10]发展了一个耦合的数值计算模型FSSI-CAS 2D 及其三维版本。该耦合模型中,波浪及其孔隙流采用RAVANS 方程控制,结构物及其海床地基的动力反应采用Biot 动力方程控制;一个耦合模块将RAVANS和Biot 动力方程耦合成整体。该模型具有以下3 个方面的优点:①几何计算模型可以很复杂,可施加多种化边界条件,如力、位移、加速度、流量、孔隙压力、周期边界、连接边界、吸收边界等。②具有较完备的海床地基土的本构模型,包括各种弹性模型,摩尔-库仑/Mises/Tesca 模型、修正剑桥模型、PZIII 模型等共20 多种本构模型,而且本构模型接口完全开放,拥有很好的适用性和灵活性。③能够用于高度非线性问题的计算。该耦合模型的有效性、适应性和准确性已经被一系列试验数据、解析解所验证[11],并已成功地在近海结构物的固结沉降[12-13]、开采扰动边坡的地震动反应[14]、近海波-结构物-海床相互作用等问题研究上得到应用[15]。
本文基于FSSI-CAS 2D为分析工具,采用砂土的高级本构模型Pastor-Zienkiewicz-Mark III(PZIII)[16]描述海床砂土的动态力学行为,定量研究波浪作用下砂性海床内波致液化的特征和动态过程。
3 计算模型及参数
计算模型如图1 所示,波浪和海流在砂性海床上方通过,给海床表面施加了周期性动态水压力。海床厚度为20 m,计算范围选择为400 m。波浪水动力参数为:周期T=8.0 s,水深d=10 m,波高H=3.0 m。该研究中,由于海流的影响不显著[17],不考虑海流的存在,即海流流速 U0=0.0 m/s。计算域的水平尺度大于波长的5 倍,足够消除侧边界的影响。
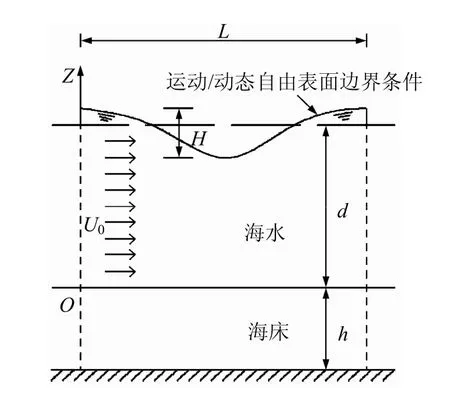
图1 波浪作用下海床发生液化的计算概意图Fig.1 Schematic of wave-induced liquefaction in loose sandy seabed
计算中采用三阶Stokes 波理论确定波浪导致的作用在海床表面的动态水压力[17]为
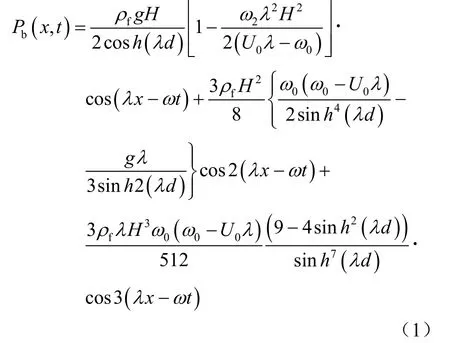
式中:g为重力加速度;ρf为海水密度;λ为波数;ω为波浪角频率;ω0为一阶波浪角频率;ω2为二阶波浪角频率,它们的计算公式分别为
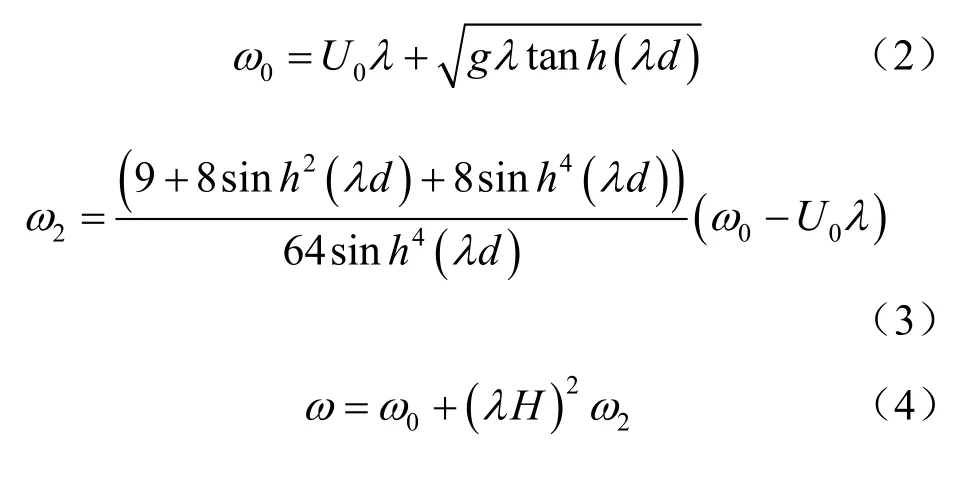
计算中用于描述海床砂土的物理属性的参数见表1。该表中的砂土参数来自内华达标准砂,由新科维奇教授在参加VELACS 项目竞赛时所标定,可信度较高。PZIII 是一个土的高级模型,描述砂土的属性所需的参数较其他简单本构模型要多,而且测试也较复杂。对于近海工程中取得的实际海床土样品,需要认真开展室内试验,才能够准确地确定PZIII 模型所需的参数。表1 中参数的物理意义可参考文献[16]。

表1 计算中采用的砂质海床土的PZIII 参数Table 1 Parameters in PZIII model used in computation for sandy seabed
4 结果分析
计算中首先确定海床在自重和静水压力作用下固结平衡状态。该状态中海床内部没有超孔隙水压力存在,只有静水压力,并符合 ρgh 的分布规律。以此固结平衡状态为初始条件,在海床表面施加静水与动水压力之和,同时保证海床表面的有效应力时刻为0。计算过程中计算域的侧边界水平方向固定,但竖直方向保持自由。分析中以计算域对称线x=200 m 上的结果为典型代表研究波浪作用下海床内的孔隙水压力、有效应力变化过程和液化特征。由于该对称线远离计算域的侧边界(大约3 个波长),水平固定的侧边界对数值计算结果基本没有影响。有限元网格剖分时以海床底部为z=0 m,水平方向网格尺寸为1 m,竖直方向尺寸为0.5 m;计算结果以压应力为负值表示。

图2 砂质海床内孔隙压力上升和有效应力减小过程Fig.2 Pore pressure build-up and effective stress increase in loose seabed
图2 显示的是海洋波浪作用下,海床内对称线上z=18 m和z=10 m 两个典型点上的孔隙压力和竖向有效应力的变化过程。可以清楚地看出,在波浪作用下,海床松散土内的累积孔隙水压力会持续上升,土颗粒间的有效应力逐渐减小。当累积超孔隙压力上升到足以克服其上覆的土重量时,粒间有效应力即接近为0,表明土已经发生了液化。液化之后累积超孔隙压力不能持续再增大,而是维持某个量级,在后续的时间里,累积的超孔隙压力会逐渐消散,但由于存在波浪周期性作用,总的孔隙水压力总存在振荡。当欠密实海床土颗粒间的有效应力减少很小时,土发生液化,成为一种黏性很高的重型流体,基本失去承载力,建于其上的海洋结构物一旦碰到此种情况,即会发生倾倒破坏。从图2还可以看出,z=18 m 处的海床土大约在t=180 s时就发生了液化,而在z=10 m 处的海床土在约t=300 s 时才发生液化,表明波浪作用下欠密实海床土的液化并不是同时发生的,而是自上而下的一个渐近性过程。
图3 是波浪持续作用43 个周期后,海床内部波浪导致的累积超孔隙压力的分布图(x=100~300 m 范围)。图3 表明,海床内部累积的超孔隙压并不是均匀分布,而是呈波浪形分布,这肯定是其上的波浪作用直接影响的结果。并且累积超孔隙压力是海床上部小、下部大。结合图2 可知,液化的发生与累积超孔隙压力的绝对值没有关系,在海床上部,即使超孔隙压力较小,也可以先发生液化,因为海床上部土的液化阻力也较小;而在海床下部,即使超孔隙压力较大,也可以不发生砂土液化。
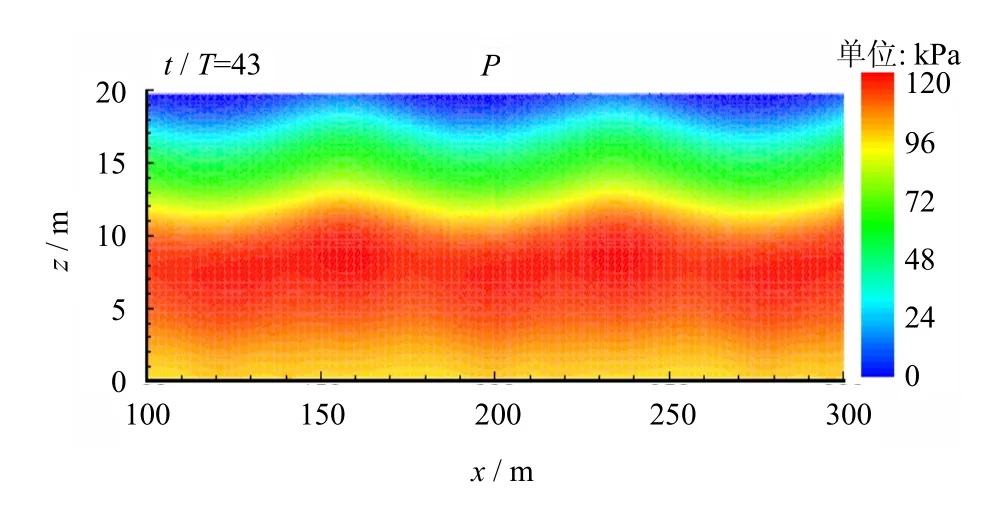
图3 砂质海床内波浪导致的累积超孔隙压力分布图Fig.3 Distribution of wave-induced cumulative excess pore pressure in loose sand seabed
波浪作用下欠密实海床土从非液化状态到液化状态过程的非线性应力-应变关系是值得一看的结果。图4 展示的是对称线x=200 m 上两个典型位置z=18 m和z=10 m 上的应力-应变关系曲线。图4表明,欠密实海床土在波浪循环荷载作用下的应力-应变关系是比较复杂的,在发生液化之前,海床土的剪应变要比液化之后小得多;液化之后,剪应变急剧快速增大,例如,液化之前z=18 m和z=10 m两处的剪应变分别不超过1.0%和0.3%;液化之后,剪应变分别达到了8.5%和2.8%。可以看出,液化后欠密实海床土的抗剪强度损失是相当可观的,海床液化土在循环剪应力作用下发生了量级很大的流动变形,即使剪应力处于很小的水平,如z=18 m处的500 Pa。为了与非常密实的弹性海床土相比较,图4 中也画出了弹性海床土的应力-应变关系(红色线)。这两处的应力-应变关系为直线,剪应变极小,也就是只存在弹性变形。非常密实的海床土的抗剪强度非常高,在波浪动力循环作用下难以发生塑性变形,不会发生累积液化,可作为近海结构物地基的理想材料。然而在海床浅部非常密实的海床土在近海环境中是较少存在的,它的形成必须是松散海床土在历史上经历很多次液化-固结过程。在近海环境中,大量存在着第四纪新近沉积的欠密实沉积物,所以在近海工程建设中,因极端天气波浪导致的结构物海床地基累积液化失稳是需要认真对待的一种失稳机制。
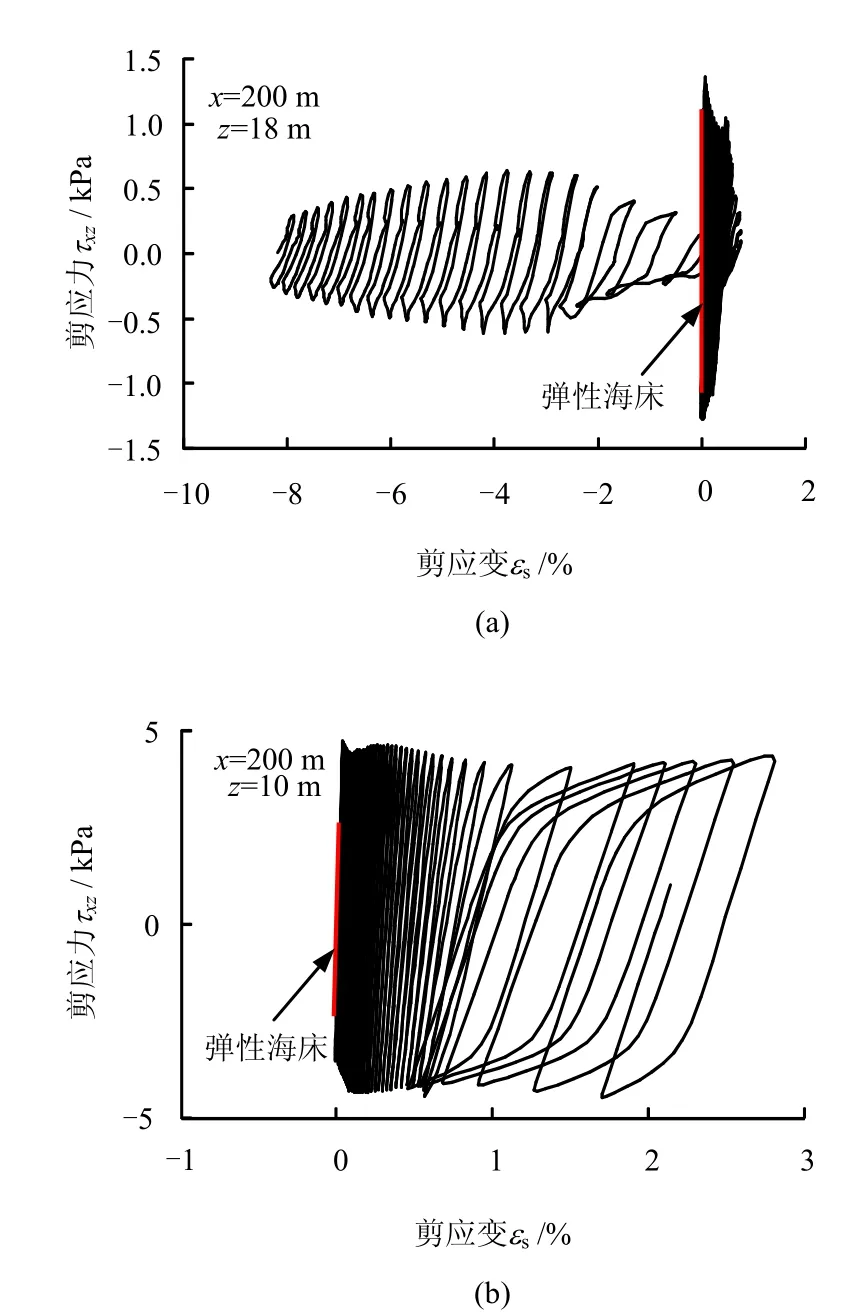
图4 波浪作用下欠密实海床内典型点上的应力-应变关系Fig.4 Stress-strain relation on typical positions in loose seabed under wave loading
结合图2 的结果,图5 可以用来进一步深入研究海床波浪导致的液化的渐近性。图中 Lr为海床土的自重应力线,也可以认为该线为海床土的液化阻抗线;根据砂土液化的物理定义,当累积超孔隙水压到达土的自重时,土即变成液化状态。图5 中不同时刻海床内部累积超孔隙水压力沿深度的分布再次有力地表明:波浪导致的海床土液化的过程是渐进的,不是同时发生,波致液化从海床表面开始,随着波浪的持续作用,液化区逐渐向海床下部扩展。从图5 看出,在t=345 s,海床内x=200 m 线上液化深度达到了11 m。图6为波浪作用下欠密实海床内渐进液化的过程,其渐进过程在一些试验中已经得到验证,但目前还很少在数值计算结果中精细地捕捉到。这个液化过程并不是无限制地一直往海床底部发展的,存在一个最终的液化深度,在本文的算例中,这个最终的液化区前缘到达z=9 m 的地方,对应的液化深度为11 m。在图5 中还可以观察到一个很有趣的现象,那就是海床内累积孔隙水压力的增长并不是无限制的,而是受到海床土自重应力线 Lr的限制,对于无黏性海床土,累积超孔隙水压力是不能够超过土和上覆结构物的自重的(对于黏性土,是可以超过的)。之前有一些文献中的计算结果就存在无黏性土中累积超孔隙水压力能够大幅度超过土的自重,尤其是在海床的浅部[18-19];这无疑违背了物理规律,因为累积超孔隙水压力一旦达到了土和上覆结构物的自重,土就发生了液化;除非此时有额外的外力施加在液化土上,否则超孔隙水压力是不能再累积增长的。
前面关于波致海床液化的结果只是点和线上的结果。图7 显示的是波浪作用20 周期后,海床内部液化区的分布形态(蓝色区域)。该图也表明,液化区的前缘也不是直线,也受波浪作用的影响。波浪作用20 个周期后,海床浅部5 m 范围内的欠密实海床土基本都液化了,失去承载力。
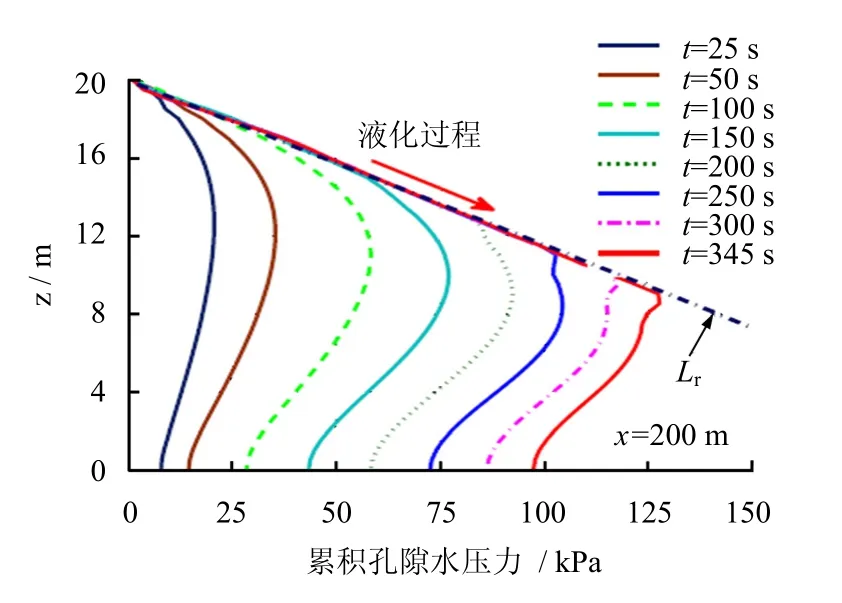
图5 累积孔隙水压力沿海床深度在典型时刻的分布图Fig.5 Vertical distribution of residual pore pressure along seabed depth at several typical times

图6 波浪作用下欠密实海床内液化区前缘深度的发展过程Fig.6 Development process of frontier of liquefaction zone in loose seabed under wave loading

图7 波浪作用20 个周期后海床内的液化区范围Fig.7 Predicted liquefaction zone in loose seabed after 20 periods wave loading
5 结 论
(1)松砂海床地基在波浪作用下其内部的超孔隙水压力上升,有效应力减少。当超孔隙水压力超过其上覆土自重、有效应力接近为0 时,土发生液化,失去承载力。液化后累积超孔隙水压力不能再持续上升。在液化后的较长时间里,累积超孔隙水压力将伴随着孔隙水排出,发生孔压消散的固结过程。累积超孔隙水压力的增长受到海床土的自重应力的限制,其不能超过土的自重应力。
(2)波浪导致的累积超孔隙水压力在海床下部大、上部小,且呈波浪形分布。液化发生与否,与超孔隙水压力的绝对值没有关系。海床表层,尽管超孔隙水压力小,液化也可以发生。
(3)波浪导致的海床土液化是一个渐进的过程,不是同时发生的,波致液化从海床表面开始,随着波浪的持续作用,液化区逐渐向海床下部扩展。液化的最终深度与波浪特征、海床土的特性密切相关。如在同等条件下,大波浪导致的液化深度肯定大;在同等条件下,渗透系数大的海床土,液化深度小,甚至不发生液化。
[1]HSU J R,JENG D S.Wave-induced soil response in an unsaturated anisotropic seabed of finite thickness[J].International Journal for Numerical and Analytical Methods in Geomechanics,1994,18(11):785-807.
[2]JENG D S.Wave-induced liquefaction potential in a cross-anisotropic seabed[J].Journal of the Chinese Institute of Engineering,1996,19(1):59-70.
[3]ZHOU X L,XU B,WANG J H,et al.An analytical solution for wave-induced seabed response in a multi-layered poro-elastic seabed[J].Ocean Engineering,2011,38(1):119-129.
[4]YAMAMOTO T,KONING H,SELLMEIJER H,et al.On the response of a poro-elastic bed to water waves[J].Journal of Fluid Mechanics,1978,87(1):193-206.
[5]OKUSA S.Wave-induced stress in unsaturated submarine sediments[J].Geotechnique,1985,35(4):517-532.
[6]SASSA S,SEKIGUCHI H.Analysis of wave-induced liquefaction of sand beds[J].Geotechnique,2001,51(2):115-126.
[7]SASSA S,SEKIGUCHI H.Wave-induced liquefaction of beds of sand in a centrifuge[J].Geotechnique,1999,49(5):621-638.
[8]王立忠,潘冬子,潘存鸿,等.波浪对海床作用的试验研究[J].土木工程学报,2007,40:101-109 WANG Li-zhong,PAN Dong-zi,Pan Cun-hong,et al.Experimental investigation on wave-induced response of seabed[J].China Civil Engineering Journal,2007,40:101-109.
[9]孙永福,董立峰,宋玉鹏.黄河水下三角洲粉质土扰动土层特征及成因探析[J].岩土力学,2008,29(6):1494-1500.SUN Yong-fu,DONG Li-feng,SONG Yu-peng.Analysis of characteristics and formation of disturbed soil on subaqueous delta of Yellow River[J].Rock and Soil Mechanics,2008,29(6):1494-1500.
[10]YE J H.Numerical analysis of wave-seabed-breakwater interactions[D].Dundee,UK:University of Dundee,2012.
[11]YE J H,JENG D S,WANG R,et al.Validation of 2 2-D semi-coupled numerical model for fluid-structure-seabed interaction.Journal of Fluids and Structures,2013,42:333-357.
[12]YE J H.Numerical modelling of consolidation of 2-D porous unsaturated seabed under a composite breakwater[J].Mechanika,2012,18(4):373-379.
[13]YE J H,JENG D S,CHAN A H C.Consolidation and dynamics of 3D unsaturated porous seabed under rigid caisson breakwater loaded by hydrostatic pressure and wave[J].Science China-Technological Sciences,2012,55(8):2362-2376.
[14]张燕,纪洪广,叶剑红.扰动岩质边坡强震作用下动力响应分析[J].煤炭学报,2013,38(增刊2):304-311.ZHANG Yan,JI Hong-guang,YE Jian-hong.Dynamic response analysis of disturbed rock slope under strong earthquake loading[J].Journal of China Coal Society,2013,38(Supp.2):304-311.
[15]YE J H,JENG D S,WANG R,et al.Breaking wave-induced response of composite breakwater and liquefaction in seabed foundation[J].Coastal Engineering,2014,85:75-86.
[16]PASTOR M,ZIENKIEWICZ O C,CHAN A H C.Generalized plasticity and the modelling of soil behaviour[J].International Journal for Numerical and Analytical Methods in Geomechanics,1990,14:151-190.
[17]YE J H,JENG D S.Response of porous seabed to nature loadings——waves and currents[J].Journal of Engineering Mechanics,ASCE,2012,138(6):601-613.
[18]RAHMAN M S,JABER W Y.Simplified drained analysis for wave-induced liquefaction in ocean floor sands[J].Soils and Foundations,1986,26(3):57-68.
[19]SUMER B M,KIRCA V S O,FREDSOE J.Experimental validation of a mathematical model for seabed liquefaction in waves[C]//Proceedings of the International Offshore and Polar Engineering Conference,[S.l.]:[s.n.],2011,1010-1018.

