基于巴西劈裂试验的页岩强度与破坏模式研究
杨志鹏,何 柏,谢凌志,李存宝,王 俊
(1.四川大学 建筑与环境学院,四川 成都 610065;2.四川大学 新能源与低碳技术研究院,四川 成都 610207;3.四川大学 能源工程安全与灾害力学教育部重点实验室,四川 成都 610207)
1 引 言
页岩气作为常规能源的有效补充,具有资源潜力大、分布面积广、发育层系多等特点。页岩最典型的特征就是具有薄片的层状节理,层理的存在使页岩在各个方向表现出了明显不同的力学响应和破坏方式[1]。研究者通过各种力学试验主要对层状岩石的基本力学参数随层理倾角的变化趋势、强度的各向异性以及破坏模式做了大量研究。如:Niandou[2]等对页岩做了静水压力和三轴压缩试验,详细分析了横观各向同性弹性参数的变化规律、塑性变形和破坏方式,并得到了弹性参数及破坏模式与围压和倾角的关系;Mokhtarit等[3]通过三轴与声波测试试验讨论了页岩破坏前、后的特性,获得了峰值破坏后残余强度与围压和倾角的关系;衡帅等[4]基于页岩直剪试验,提出了剪应力集中系数,根据剪切机制研究了层理面的力学性质,得到了不同层理面角度下抗剪强度各向异性的试验结果;李庆辉等[5]通过三轴试验分析了页岩在不同围压下随层面角度变化的破坏模式;徐敬宾[6]等从纵波波速测试、单轴压缩和三轴压缩试验等,研究了页岩固有的各向异性及变形特征。
巴西劈裂试验是测量岩石抗拉强度的一种简单而有效的方式。目前对层状岩体的巴西劈裂抗拉强度特性,主要从试验和数值两方面开展了力学参数和破坏方式随层理方向变化规律的研究。如:Sierra等[7]基于巴西劈裂、声发射、超声波等试验研究得到了矿物组成、形态和岩相组成对页岩各向异性程度的影响;Chen等[8]针对横观各向同性的琥珀展开了中间带孔的圆盘巴西劈裂试验,分析了不同层理方向的抗拉强度,并运用边界元法获得了孔周围的应力分布;Chou[9]、Ye[10]等分别从反算、迭代的数值和试验方法研究了横观各向同性琥珀的弹性参数变化规律;Vervoot等[11]对9种不同种类的横观各向同性岩石做了巴西劈裂试验,将最终破坏后的裂纹归纳为中央区、非中央区和层面主导的3种模式,分析并得到了每种破坏模式与层理方向的关系;谭鑫等[12]对非均质的片麻岩的抗拉强度做了物理试验和数值模拟,解释了劈裂破坏形式产生的机制,揭示岩石在荷载状态下破裂过程的本质。
针对页岩的抗压强度及破坏模式国内外学者做了比较多的研究,特别是针对页岩在不同围压、不同倾角下的强度、变形与破坏模式等有了很细致的分析。虽然目前也有学者对横观各向同性岩体进行了抗拉特性的相关试验,主要都是针对板岩、片麻岩和层状砂岩等的研究。但基于巴西劈裂下对页岩的强度及破坏模式下系统性的研究较少。在实际的水力压裂过程中,当地应力相差较大,原生裂隙方位与主应力成30°~60°且注入流体黏度较低时,地层容易沿原生裂隙诱发剪切破裂,但一般情况下,地层的张拉破裂更容易发生[13],所以很有必要针对页岩的抗拉性质做系统的分析。本文对不同层理方向下的页岩展开了巴西劈裂和并声发射试验,对页岩的抗拉强度及破坏形态随层理倾角的变化做了仔细研究,并分析了页岩声发射空间演化分布规律和分形维数特征与层理方向的关系。
2 页岩巴西劈裂试验材料与设备
本次试验的试件取自重庆市彭水县漆辽海相志留统龙马溪组的页岩露头。该地层为灰黑色的页岩,层理面清晰可见,呈波痕状发育。在试件的加工过程中首先采用干钻法沿页岩层理面钻取直径为50 mm的岩芯(见图1(a)),得到Φ50 mm的圆柱体试件(见图1(b)),然后将圆柱体每隔25 mm切割成Φ50 mm×H25 mm的圆盘(见图1(c))。按照国际岩石力学学会的标准,巴西圆盘试样上、下表面的平行度控制在 0.5 mm,表面的平整度控制在0.1 mm。试验的倾角θ规定为加载方向与层理面法向的夹角(见图2(a))。为了保证θ的准确性,以过圆盘中心点的层理为基线,用量角器量取7个角度,分别为 0°、15°、30°、45°、60°、75°和90°,每个角度测试3个试件,共27个。试验在四川大学MTS815 Flex Test GT岩石力学试验系统上完成,同时采用美国PAC公司18位A/D,1~3 MHz带宽频率范围的 PCI-2声发射系统。MTS815电液伺服控制力学试验系统为全数字计算机自动控制系统,轴向荷载0~4600 kN,轴向位移±50 mm,轴向和环向变形引伸计量程分别为−4.0~4.0、−2.5~12.5 mm,可实时记录荷载、应力、位移和应变值,并同步绘制荷载-位移、应力-应变曲线。PCI-2声发射系统可对变形破坏中的声发射事件自动计数、存储,波形的采集与分析,实现声射的实时监测,最大信号幅度为100 dB,动态范围大于85 dB。全程采用线性可变差动传感器(LVDT)进行轴向位移控制,位移加载速率为0.05 mm/min。采用8个声发射探头分布于页岩的表面进行探测(见图2(b)),并涂上凡士林以增强探头与试样的接触效果,然后用胶带固定,以减少声发射信号的衰减。
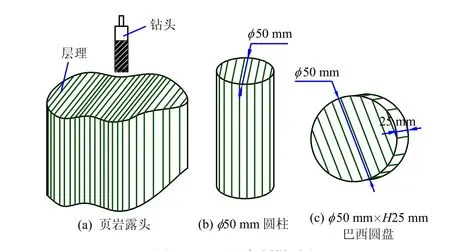
图1 巴西圆盘制样过程Fig.1 The techniques to drill Brazilian disk
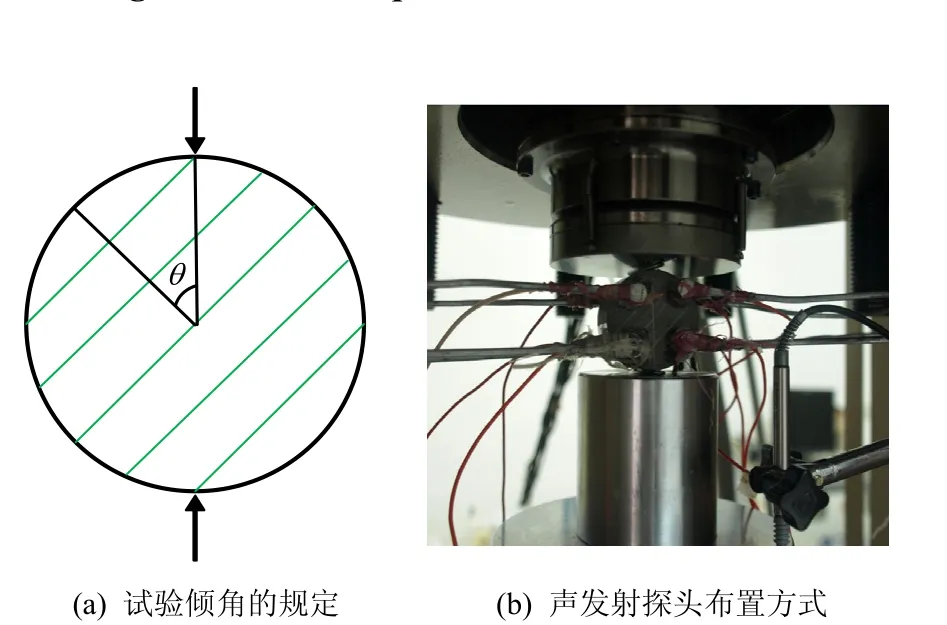
图2 倾角θ 及声发射探头布置方式Fig.2 Angle of inclination θ and arrangement of the acoustic emission sensors
3 试验结果及分析
3.1 巴西劈裂试验结果
根据经典弹性力学,可以得到试样的劈裂强度公式为
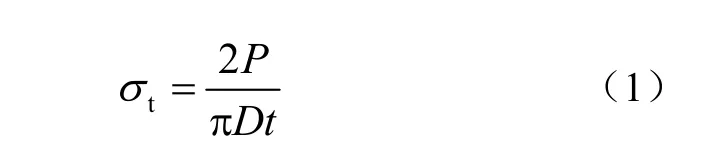
式中:P为破坏荷载;D、t分别为试件的直径和厚度。
表1为7组页岩巴西圆盘的劈裂强度值。图3为页岩圆盘试件在不同倾角下的劈裂强度变化趋势。其中黑色短线为每个巴西圆盘的试验值,灰色垂线为该组试验值的变化范围,黑色样条曲线为每组试件劈裂强度平均值的变化趋势。
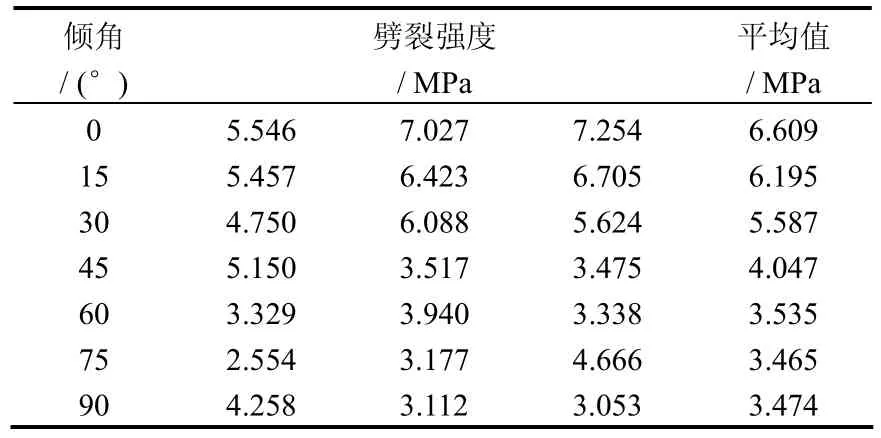
表1 页岩巴西劈裂强度值Table 1 Tensile strength of shale from Brazilian test
从图3可知,页岩巴西圆盘的劈裂强度随着倾角θ的增大而逐渐减小。这是因为层理是薄弱面,抗劈裂的能力较低。60°以后减小的趋势不再明显,劈裂强度趋于稳定;最大值出现在θ=0°的情况下,平均为6.609 MPa;当θ=75°时,劈裂强度最小,为3.465 MPa。根据文献[11],用垂直于层理方向的劈裂强度与平行于层理方向的劈裂强度的比值来表征页岩的各向异性程度,该系数为1.9。因此,可知层理的方向对劈裂强度有着较强的影响。
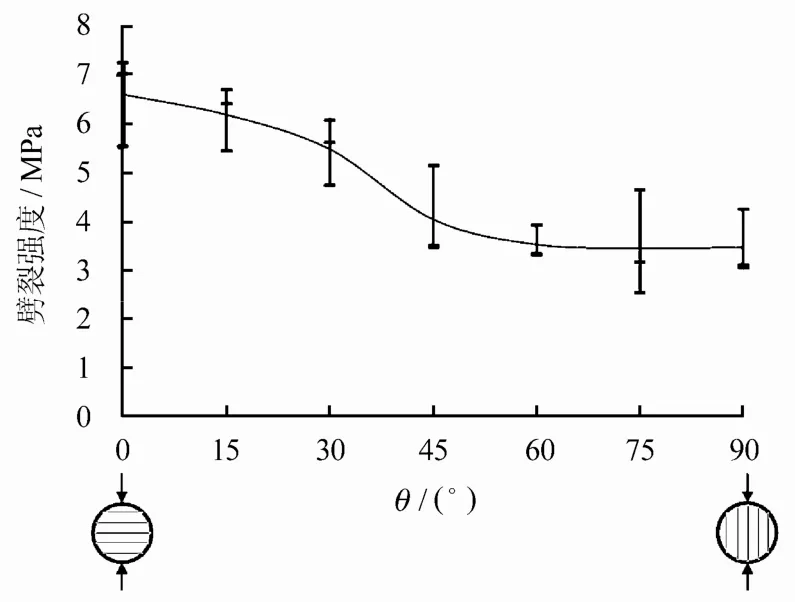
图3 不同倾角θ 下的页岩劈裂强度变化趋势图Fig.3 Variation of tensile strength as a function of the angle of inclination θ for shale
图4为所有不同倾角下的巴西圆盘的破坏模式图。可以看到:当θ=0°或θ=90°时,圆盘首先从两端起裂(这一点也可以从空间声发射点分布图9得知),而后裂纹穿过圆盘中心贯通整个试件,最后形成一条竖向裂缝,此时的圆盘试样表现为直线形的破坏方式。对于这两种情况下用式(1)计算的劈裂强度,可分别视为基质的劈裂强度和层理的劈裂强度。当0°θ<<90°时,圆盘的破坏方式较为复杂,但裂纹均未通过圆盘中心,大概可归纳为两种形态:15°试件的裂纹呈现一种月牙形,即裂纹在两压条处起裂,在试件中部向一侧凸出;而30°、45°、60°和75°的试件则表现出曲弧形的破坏裂纹,即裂纹只在一端起裂,另一端则偏离加载点一段距离,裂纹向一侧倾斜。特别地当θ=45°时,裂纹表现出了沿着层理发展的态势;当θ=75°时,裂纹的方向基本平行于层理的方向。综上所述,由于页岩的层理特性的影响,可将页岩巴西劈裂试验后的最终破坏模式归纳为3种:月牙形、曲弧形和直线形,如图5所示。
3.2 试验破坏模式分析

图4 不同倾角θ 下的页岩巴西劈裂破坏模式图Fig.4 Fracture modes of shale under Brazilian tests with different inclination angles

图5 页岩巴西劈裂3种典型破坏模式Fig.5 Three typical fracture patterns of shale under Brazilian test
层理面的弱胶结是影响页岩强度各向异性的主要因素[14]。因此,出现以上3种形式的破坏模式,主要是由于沿层理在不同倾角下的应力分解达到了层理的抗拉或抗剪强度。这里采用Claesson等[15]给出的公式,可以得到横观各向同性巴西圆盘中心点的应力大小。
圆盘中心点的拉应力为
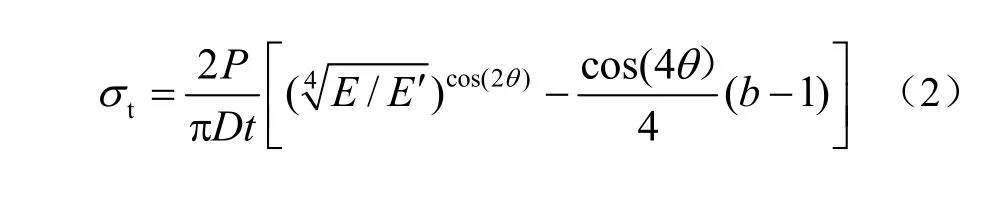
圆盘中心点的压应力为

式中:E′为垂直各向同性面的弹性模量;E为平行各向同性面的弹性模量;υ′为垂直于各向同性面内的泊松比;G′为垂直于各向同性面内的剪切模量。利用单轴试验,可以得到E′、E、υ′的值,而G′则根据文献[16]求得,结果见表2。

表2 页岩横观各向同性力学参数值Table 2 Transversely isotropic parameters of shale
衡帅等[4]曾用直剪试验获得了层理和基质的剪切强度特征参数(见表3)。

表3 页岩的抗剪强度参数Table 3 Shear strength parameters of shale
对于任意倾角下的圆盘中点的应力,总可以将其沿着层理方向和垂直于层理方向进行应力分解,如图6所示,可得到式(4)、(5)。
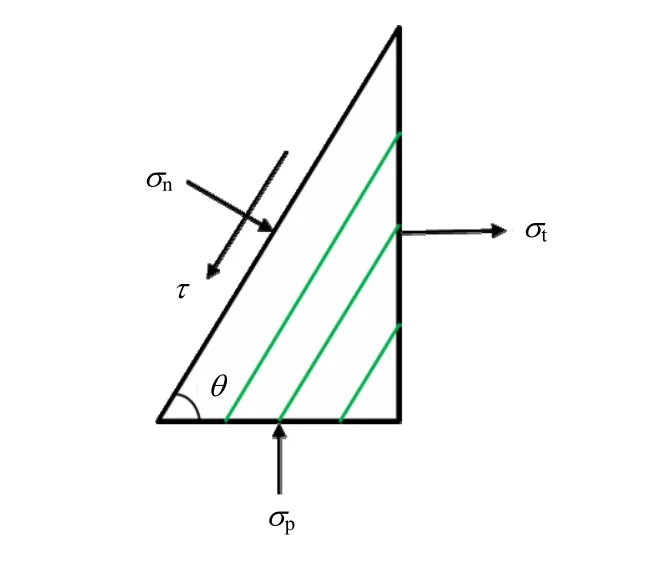
图6 沿层理方向分解得到的正应力与剪应力分量Fig.6 Normal stress and shear stress components along the bedding plane
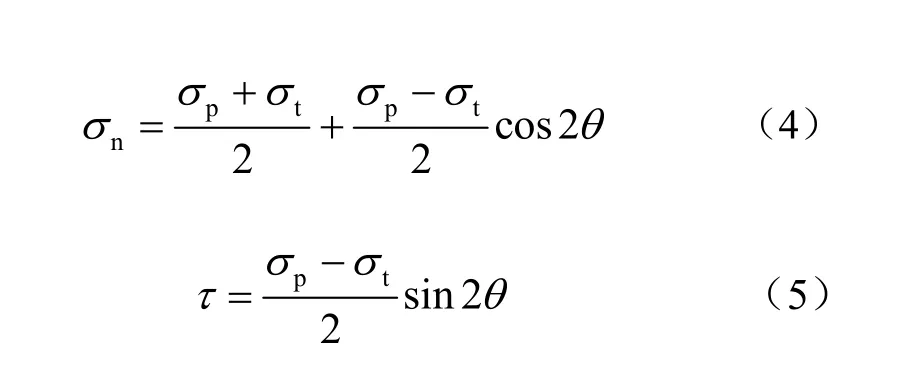
假定层理和基质的强度符合Mohr-Coulomb准则,并规定压应力为正,拉应力为负。则沿层理和基质的破坏条件可分别写为
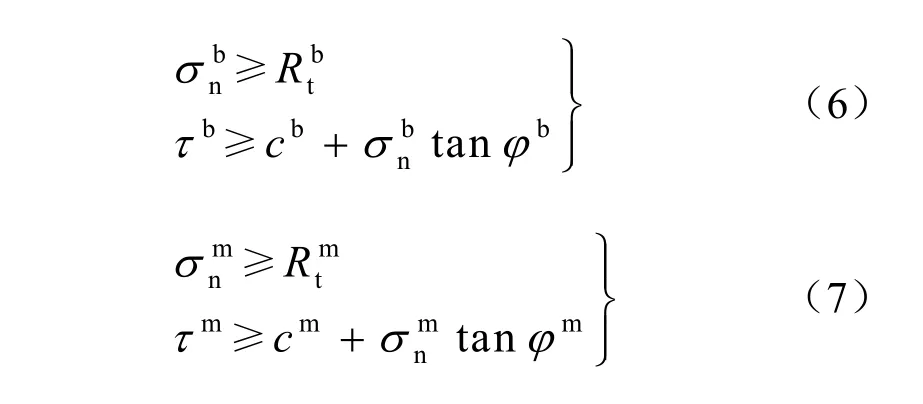
当θ=0°时,如图7所示,由式(4)、(5)可知:τ=0,即层面上只有正应力而没有剪应力,试件将不会沿着层理发生剪切破坏。同样,层理受压应力作用,也不会沿层理发生拉破坏。此时由式(2)计算得圆盘中心点拉应力大小为σt=7.168 MPa大于基质的抗拉强度,故而只可能是因为基质达到抗拉强度而发生拉伸破坏。
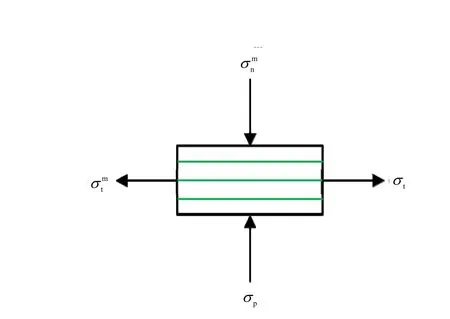
图7 当θ=0°时,基质发生拉伸破坏Fig.7 The tensile failure of matrix when θ=0°
当θ=90°时,如图 8所示,由式(4)、(5)可知:τ=0,σn=σt,同样层面上只有正应力而没有剪应力,此时试件也不会沿着层理发生剪切破坏,由于,即沿层理分解得到的正应力达到了层理的抗拉强度,因此,试件将沿着层理发生拉伸破坏。

图8 当θ=90°时,层理发生拉伸破坏Fig.8 The tensile failure of bedding plane when θ=90°
当0°<θ<90°时,并将θ=0°和θ=90°一并表示在图9中,图中共有和两套坐标系。将层理的抗剪强度线和抗拉强度线表示在坐标系中,基质的抗剪强度线和抗拉强度线表示在坐标系中。散点为式(4)、(5)所得到的不同倾角下沿层理的正应力与剪应力。从图中可以得知,0°~90°试样点的分布规律类似于一个半圆形。0°试样的点主要分布在基质的抗拉强度线两侧,90°试样的点主要分布在层理的抗拉强度线两侧,因此,该两组试件的破坏分别以基质和层理的拉伸破坏为主;而15°、30°、45°、60°和75°试样的点分布在包络线以内,其中15°试样的点靠近基质的抗拉强度线,30°、45°和60°试样分布在包络线中部,75°试样的点靠近层理的抗拉强度线,由此说明,当 15°≤θ≤75°时,试样的破坏主要为基质和层理的复合型破坏,其中15°和75°试样为复合型拉伸破坏,30°、45°和60°试样为复合型剪切破坏。值得注意的是,15°~75°试样的点分布在强度包络线以内,这并非意味着这4组试件未发生破坏,只能说明破坏面离中心点的距离较远,毕竟式(2)、(3)给出的是圆盘中心点的应力大小。

图9 不同层理角度下的应力大小与强度的比较Fig.9 Comparison of stress and strength at different angles of inclination
4 声发射结果及分析
4.1 声发射时间和空间序列特征
声发射的时间序列特征是指岩石内部破裂时声发射参数随时间的变化关系,这些参数主要包括:振铃计数、振铃计数率、能量计数和能量计数率[17]。声发射的空间序列特征是指岩石在承受荷载的过程中,局部因能量的快速释放而发出瞬态弹性波,并伴随着损伤演化和微破裂的产生发展。通过研究声发射三维空间定位点的分布,可以捕获岩体发生破裂位置,分析破坏演化规律。在7组试件中选取一个典型试件,在3种应力水平(σ/σmax)下每个试件的声发射点空间累计分布情况如图10所示。
从声发射空间累计定位演化情况可以看出:在应力水平较低时(σ/σmax=10%),由于加载点两端应力集中的缘故,只有30°、45°、60°和75°试样的两端出现了零星的几个声发射点,而其他 3组角度试样均未出现声发射点。随着应力水平的增加,试样内部损伤持续累积,声发射点逐渐在试样的中部出现。当达到峰值应力时,试样内部的微破裂贯通形成宏观裂纹,声发射点大量出现;其中0°和90°试样的声发射点相对较少,但主要分布在试样的中轴线两侧,反映了试样直线型的破坏方式;30°、45°、60°和75°试样的声发射点表现出一端较密而另一端较稀疏的现象,这与曲弧型模式中的裂纹偏离加载点一段距离的破坏方式相对应;对于15°试样虽然在一端出现了较密的声发射点,但在试样的中部和另一端也累积了分布较为均匀的声发射点,大致类似月牙型的破坏方式。基于以上分析得知:声发射点的空间分布特征较好地反映了试样的宏观破坏模式。
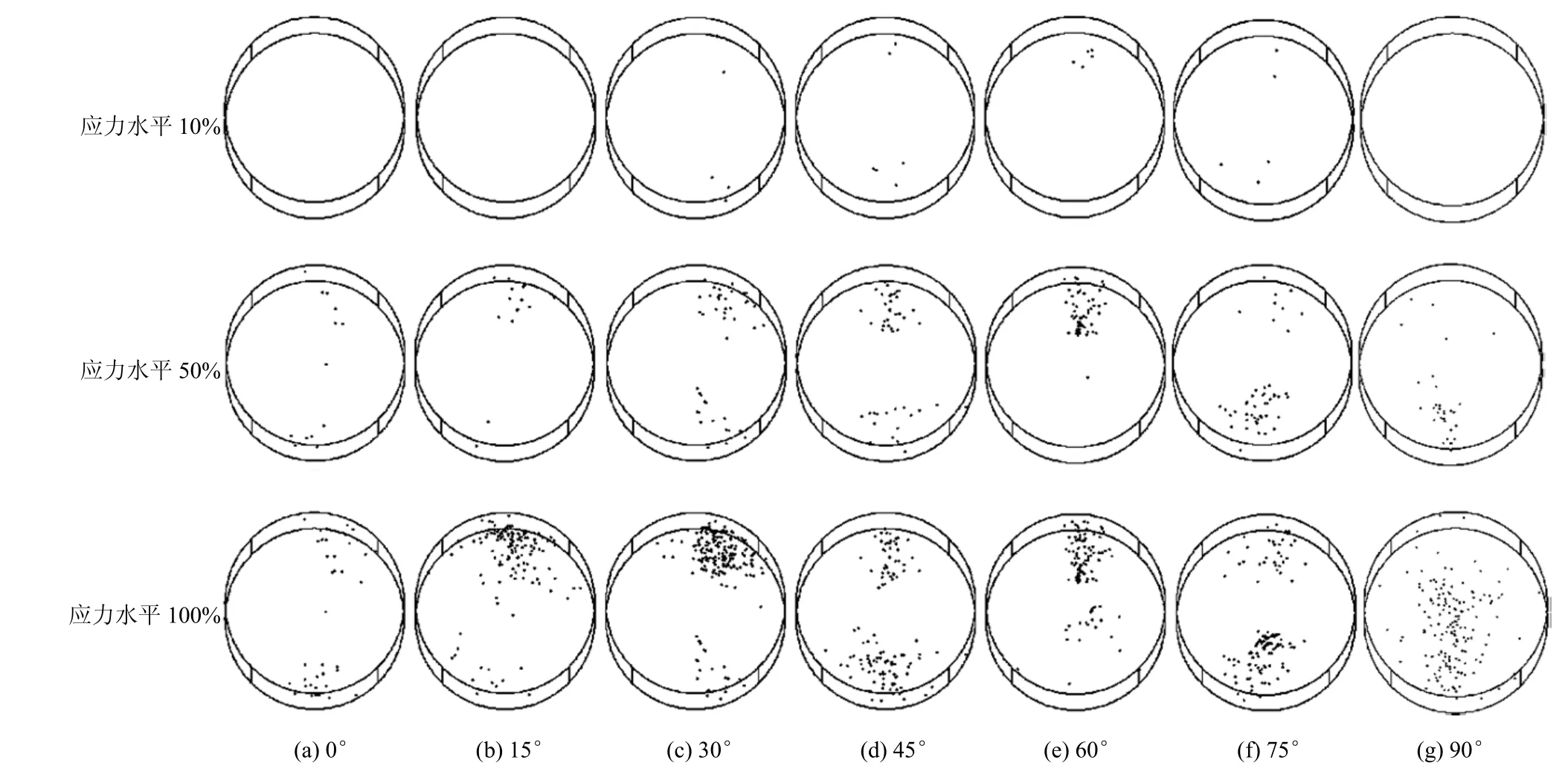
图10 不同倾角、不同应力水平下声发射点位空间分布图Fig.10 Spatial distributions of AE events at different and stress levels angles of inclianation
4.2 声发射结果的分维信息
利用覆盖法来测定物体的分形维数是最普遍的方法。由离散体构成的自然分形,其数目-半径关系可定义为[18]
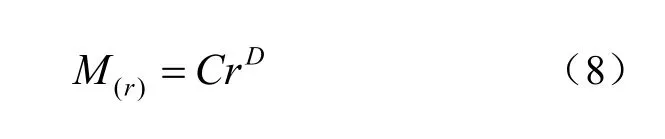
式中:r为用来覆盖自然离散体的圆的半径;M(r)为半径r的圆内所包含的离散体数目;C为材料常数;D为所获得的维数也即集束维数。将上式两边同时取对数,可得
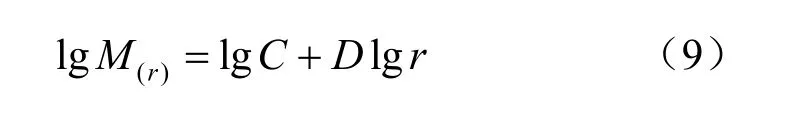
在对数坐标中绘制过性声lgM(r)-lgr曲线,并用最小二乘法对其线性段进行拟合,若两个变量的拟合结果具有较好的线性相关性,则可认为试样损伤演化程中在不同荷载下声发射的空间定位具有分形特。针对巴西圆盘试件,利用柱形覆盖法[19]来获得发射点位数目,即以圆柱形试样质心为基点,取与试样高径比成比例的小圆柱(半径r,高度h),同时扩大r和h,再统计各圆柱体内覆盖的声发射定位点数目 lg M(r),如图11所示。
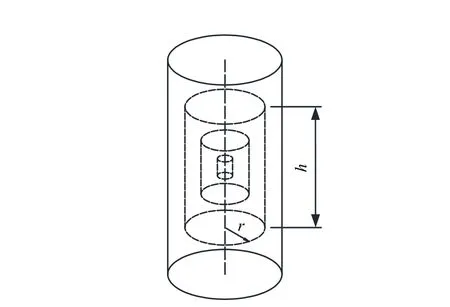
图11 柱形覆盖法Fig.11 The column covering fractal method
图12~14分别展示了应力水平、倾角、分形维数、AE能量之间的各种变化关系图。表4列出了7组倾角下试样的声发射能量值和分形维数值。在图12中,当应力水平小于70%时,各组角度下AE能量曲线的增加幅度较平缓,变化趋势相当;当应力水平超过80%时,30°试样的AE能量迅速陡增直至达到最大,90°、15°试样次之,而0°试样的AE能量值最小,这说明30°试样在承受荷载后的损伤及破裂释放的能量最大,最终破坏程度最为剧烈,内部的损伤也最严重。
从图13中的曲线可知,在所有层理角度下,随着圆盘内部的损伤持续累积,分形维数值都随着应力水平的增加而不断增大。其中,0°、15°和90°试件的分形维数值相比其他角度下普遍较低。当应力水平介于10%~40%时,45°、60°和75°试样的分形维数值增加较快,而后各个角度下试样的分形维数值增加的趋势大致相同;最后30°和45°试样在应力峰值时的分形维数达到最大,分别为:D=2.630和D=2.592。根据上述描述,说明层理和基质共同承受荷载后相比于单纯的层理或基质发生的拉破坏更容易导致微裂缝的产生。
忽略图14中曲线个别点的值可知,倾角‒分形维数的曲线变化呈倒V形分布。当应力达到峰值时,0°和90°试样的D=1.693和D=2.088,30°试样的分形维数值最大,为D=2.630。进一步分析原因可知,0°和90°试样的破坏裂纹呈直线形,微破裂沿着圆盘中线两侧分布,此时的破裂面类似于一个平面,故而分形维数值较小。对于宏观破坏模式表现为月牙形的试件(θ=15°),其分形维数值D=2.242,小于分形维数值介于2.3~2.7的曲弧形破坏方式。因此,D值越大,说明试件破坏的程度越复杂,试件内部的损伤越多,破坏后的断面呈曲率半径较大的弧面;相反D值越小,损伤的程度弱,破裂面也就越平直。将以上所描述的内容描述在三维(应力水平-倾角‒分形维数)坐标系中,如图15所示,可以清楚地得到三者之间的变化关系。这里从分形的角度再次描述并印证了层理方向对页岩破坏模式的影响。
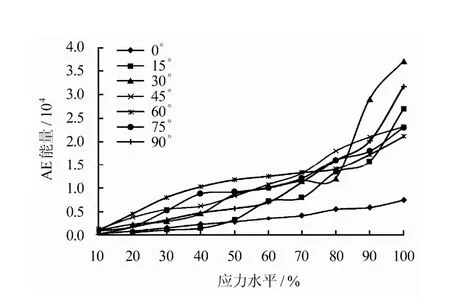
图12 不同倾角下应力水平与AE能量关系图Fig.12 Relationships of stress level with the AE energy at different angles of inclination
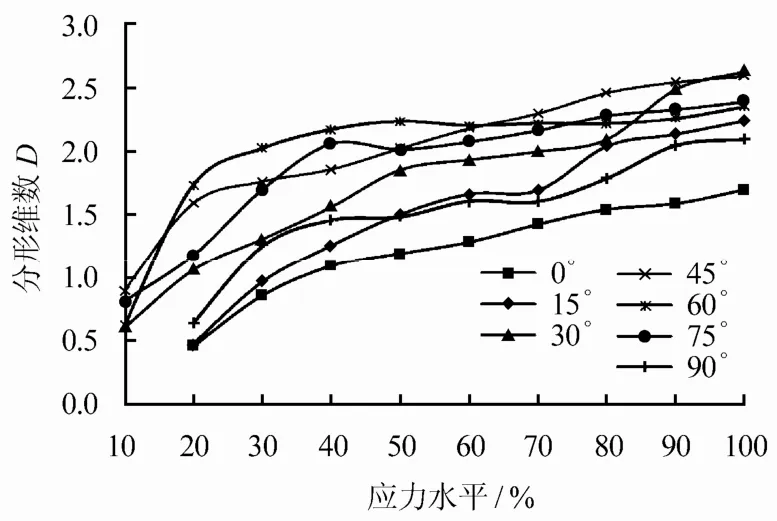
图13 不同倾角下应力水平与分形维数关系图Fig.13 Relationships of stress level with the fractal dimension at different angles of inclination
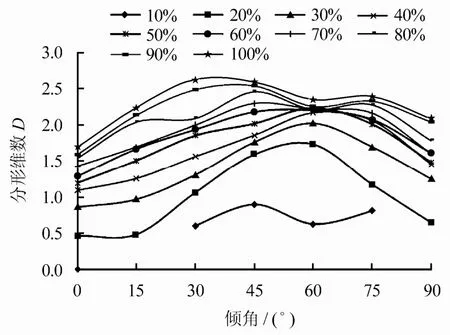
图14 不同应力水平下倾角与分形维数关系图Fig.14 Relationships of angle of inclination with the fractal dimension under different stress levels
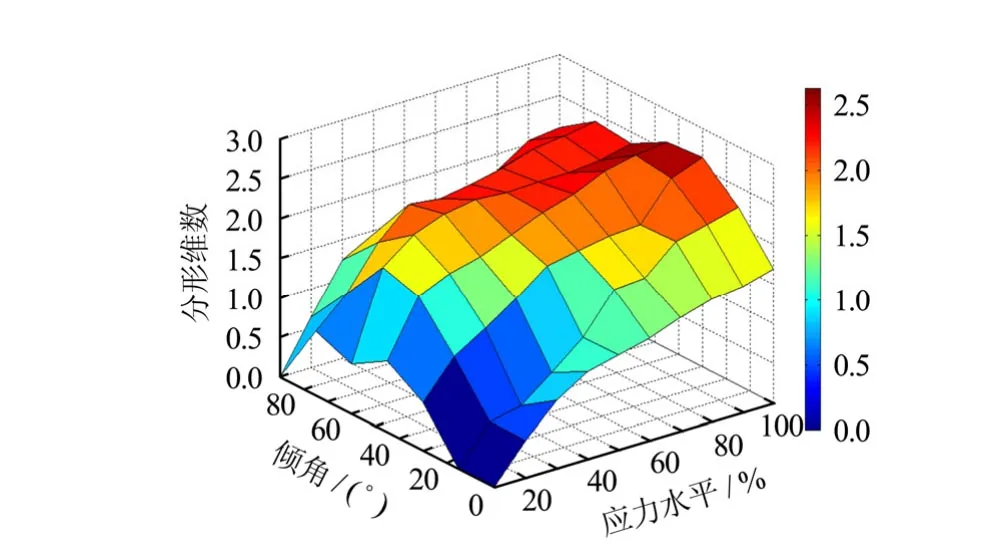
图15 应力水平-倾角-分形维数关系图Fig.15 Relationships between stress level-inclination angle-fractal dimension
5 讨 论
虽然式(1)不再适用于计算横观各向同性岩石的抗拉强度,但直线形(θ=0°和90°)这种破坏方式,符合式(1),认为劈裂破坏后的裂纹是一条位于加载平面内的垂直裂缝,因此,用式(1)计算得到的抗拉强度值作为基质和层理的抗拉强度是可行的。然而当层理方向与加载平面存在一定夹角时的月牙形、曲弧形的裂纹形态,试件的破坏是由拉应力和剪应力综合作用而导致的结果,故而抗拉强度的概念不再适用于这两种情况。CHO等[20]曾表明过应该充分考虑到混合失效模式和裂缝的位置来准确地计算出抗拉强度值。基于这种考虑,在3.1节用劈裂强度来代替抗拉强度。对于θ=15°、30°、45°、60°和75°这几种情况,由于压条位置摆放的偏差和端部摩擦等因素的影响,造成部分试件的裂纹未在压条处尖灭。理想的情况下,这几组角度的破坏方式应该都呈现月牙形,且月牙形的曲率半径应该随着角度的增大不断增加。从图9的应力与强度比较图中,可以大致判别每组角度下试样的破坏类型。若从分形维数方面来考虑,当应力接近破坏应力峰值时,试件内部的声发射点大量聚集在裂缝附近,D值大者,说明试件破坏的曲率半径也越大。因此,D值可以将试件内部的微破裂和损伤与宏观破坏形态相结合,这也为分析横观各向同性岩石的巴西劈裂破坏模式提供了一种定量的方法。
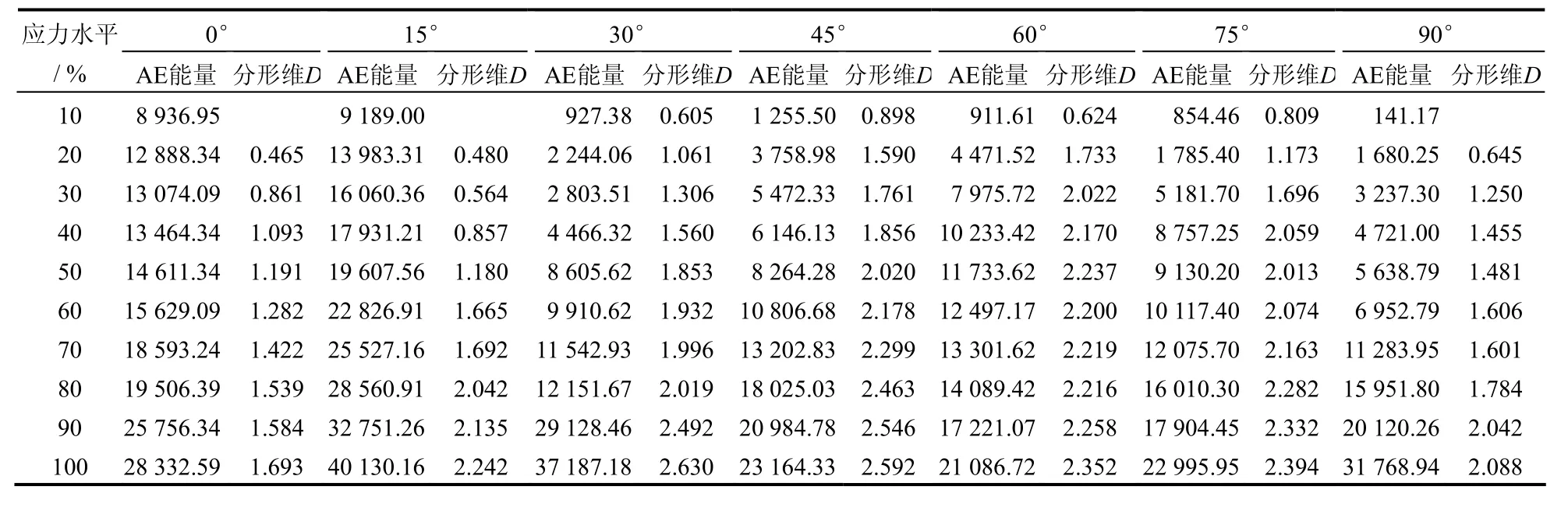
表4 AE能量与分形维数值Table 4 Results of the AE energy and fractal dimension
6 结 论
(1)页岩试样强度的各向异性性质表现明显,随着倾角θ的增大,试样的劈裂强度逐渐减小,60°以后减小的趋势不再明显,劈裂强度趋于稳定,最大劈裂强度值约为最小劈裂强度值的1.9倍。
(2)页岩试样在不同倾角下的破坏模式也有较大的差异性:根据破坏后的裂纹形态可归纳为直线型、月牙型和曲弧型3种类型。出现这3种破坏模式一方面是由于页岩在沉积时颗粒排列的不均匀性导致裂纹在扩展时发生了转向;另一方面是由于层理的胶结程度较弱,在圆盘中心点沿层理在不同倾角下分解得到的应力达到了层理的抗拉或抗剪强度。前者需要在后续工作中对页岩进行断裂韧性的研究,在本文中主要分析了后者的影响,即当θ=0°、90°时分别为基质和层理的拉伸破坏,当 15°≤θ≤75°时主要为基质和层理的复合型破坏。
通过捕捉试样内部的声发射点位发现:由于层理方向的影响,导致声发射点出现了偏移,使其大致分布在宏观裂隙周围,从而将声发射点位分布与直线型、月牙型和曲弧型3种破坏模式结合起来,分析试样内部微破裂的位置以及破坏的整个过程中的裂纹发展趋势,这从定性的角度来描述试样的破坏模式。
由于声发射的空间点位分布具有分形的特征,分形维数值随倾角的增加表现为倒 V型的分布趋势。若裂纹较直,则分形维数值较小且趋近于2;随着裂纹曲率半径的增加呈现出三维的特性,则分形维数值也相应地变大。因此,分形维数值的大小可以反映试样破坏模式,即直线型破坏模式的分形维数值最小,月牙型和曲弧型的分形维数值依次增大,这从定量的角度说明了试样的破坏模式。
(3)页岩在水力压裂过程中是一个复杂、多因素的破坏过程,由于地质沉积环境的不同导致页岩在力学性质上有所差异,水力裂缝在延伸扩展的过程中可能会因为层理的方向而发生转向,使裂纹沿着层理发生开裂,难以形成裂缝网络,故而在压裂时应综合分析射孔位置和层理方向的关系。本文只是为研究页岩的力学性质和破坏模式提供一种思路,特别是在层理方向对破坏模式的影响中做了较为细致的分析,在后续工作中将开展围压等因素对页岩强度、变形和断裂韧性的影响。
[1]LISJAK A,GRASSELLI G,VIETOR T.Continuumdiscontinuum analysis of failure mechanisms around unsupported circular excavations in anisotropic clay shales[J].International Journal of Rock Mechanics and Mining Sciences,2014,65: 96-115.
[2]NIANDOU H,SHAO J F,HENRY J P.Laboratory investigation of the mechanical behaviour of tournemire shale[J].International Journal of Rock Mechanics and Mining Sciences,1997,34(1): 3-16.
[3]MOKHTARI M,ALQAHTANI A A,TUTUNCU A N.Failure behavior of anisotropic shales[C]//47th US Rock Mechanics/Geomechanics Symposium.[S.l.]: American Rock Mechanics Association,2013.
[4]衡帅,杨春和,曾义金.基于直剪试验的页岩强度各向异性研究[J].岩石力学与工程学报,2014,33(5): 874-883.HENG Shuai,YANG Chun-he,ZENG Yi-jin.Anisotropy of shear strength of shale based on direct shear test[J].Chinese Journal of Rock Mechanics and Engineering,2014,33(5): 874-883.
[5]李庆辉,陈勉,金衍,等.含气页岩破坏模式及力学特性的试验研究[J].岩石力学与工程学报,2012,31(增刊2): 3763-3771.LI Qing-hui,CHEN Mian,JIN Yan,et al.Experimental research on failure modes and mechanical behaviors of gas-bearing shale[J].Chinese Journal of Rock Mechanics and Engineering,2012,31(Supp.2): 3763-3771.
[6]徐敬宾,杨春和,吴文.页岩力学各向异性及其变形特征的试验研究[J].矿业研究与开发,2013,33(4): 16-20.XU Jing-bin,YANG Chun-he,WU Wen.Experimental study of mechanics anisotropy and deformation characteristics of shale gas[J].Mining Research and Development,2013,33(4): 16-20.
[7]SIERRA R,TRAN M H,ABOUSLEIMAN Y N.Woodford shale mechanical properties and the impacts of lithofacies[C]//Proceedings Symposium on the 44th US Rock Mechanics Symposium and 5th US——Canada Rock Mechanics Symposium.Salt Lake City: [s.n.],2010:1-10.
[8]CHEN C S,HSU S C.Measurement of indirect tensile strength of anisotropic rocks by the ring test[J].Rock Mechanics and Rock Engineering,2001,34(4): 293-321.
[9]CHOU Y C,CHEN CHAO-SHI.Determining elastic constants of transversely isotropic rocks using Brazilian test and iterative procedure[J].International Journal for Numerical and Analytical Methods in Geomechanics,2008,32(3): 219-234.
[10]YE JIANHONG,WU F Q,SUN J Z.Estimation of the tensile elastic modulus using Brazilian disc by applying diametrically opposed concentrated loads[J].International Journal of Rock Mechanics and Mining Sciences,2009,46(3): 568-576.
[11]VERVOORT A,MIN K B,KONIETZKY H,et al.Failure of transversely isotropic rock under Brazilian test conditions[J].International Journal of Rock Mechanics and Mining Sciences,2014,70: 343-352.
[12]谭鑫,KONIETZKY H.含层理构造的非均质片麻岩巴西劈裂试验及离散单元法数值模拟研究[J].岩石力学与工程学报,2014,33(5): 938-946.TAN Xin,KONIETZKY H.Brazilian splitting tests and numerical simulation by discrete element method for heterogeneous gneiss with bedding structure[J].Chinese Journal of Rock Mechanics and Engineering,2014,33(5): 938-946.
[13]赵阳升.多孔介质多场耦合作用及其工程响应[M].北京: 科学出版社,2010: 358-359.ZHAO Yang-sheng.Multi-field coupling effect and engineering response of porous medium[M].Beijing:Science Press,2010: 358-359.
[14]衡帅,杨春和,郭印同.层理对页岩水力裂缝扩展的影响研究[J].岩石力学与工程学报,2015,34(2): 228-237.HENG Shuai,YANG Chun-he,GUO Yin-tong.Influence of bedding planes on hydraulic fracture propagation in shale formations[J].Chinese Journal of Rock Mechanics and Engineering,2015,34(2): 228-237.
[15]CLAESSON J,BOHLOLI B.Brazilian test: stress field and tensile strength of anisotropic rocks using an analytical solution[J].International Journal of Rock Mechanics and Mining Sciences,2002,39: 991-1004.
[16]EXADAKTYLOS G E.On the constraints and relations of elastic constants of transversely isotropic geomaterials[J].International Journal of Rock Mechanics and Mining Sciences,2001,38(7): 941-956.
[17]曹树刚,刘延保,张立强.突出煤体变形破坏声发射特征的综合分析[J].岩石力学与工程学报,2007,26(增刊1): 2794-2799.CAO Shu-gang,LIU Yan-bao,ZHANG Li-qiang.Study on characteristics of acoustic emission in outburst coal[J].Chinese Journal of Rock Mechanics and Engineering,2007,26(Supp.1): 2794-2799.
[18]谢和平.分形岩石力学导论[M].北京: 科学出版社,1997: 27-28.XIE He-ping.Introduction to rock fractal mechanics[M].Beijing: Science Press,1997: 27-28.
[19]XIE H P,LIU J F,JU Y,et al.Fractal property of spatial distribution of acoustic emissions during the failure process of bedded rock salt[J].International Journal of Rock Mechanics and Mining Sciences,2011,48(8):1344-1351.
[20]CHO J W,KIM H,JEON S,et al.Deformation and strength anisotropy of Asan gneiss,Boryeong shale,and Yeoncheon schist[J].International Journal of Rock Mechanics and Mining Sciences,2012,50: 158-169.

