吸力式筒形基础沉贯过程的大变形有限元模拟

吕 阳，王 胤，杨 庆

（大连理工大学 海岸和近海工程国家重点实验室，辽宁 大连 116023）

1 引 言

吸力式筒形基础作为一种优良的基础形式，已广泛应用于深海平台、海洋浮动式结构等[1]，相比于传统的基础形式，具有安装简便、成本低、施工效率高等优点。依靠负压安装到海底泥土中，是吸力筒区别于传统桩基的一大显著特点。然而正是由于这种独特的负压沉贯安装方式，吸力筒的安装过程还存在不同程度的不确定性，如在安装过程中会遇到诸如筒内形成土塞阻碍筒基下贯、安装负压过大使筒基周围土体强度失效等问题。筒基能否顺利安装并下贯到设计深度将直接影响到它能否发挥抗拉拔承载作用[2]。

由于吸力式筒基试验的难度和成本较高，随着计算理论和方法的发展，数值仿真模拟成为一种重要的研究方法，其中有限元法被广发的应用于工程领域[3]。近年来，国内外学者采用了多种有限元方法去研究吸力筒的贯入过程。Andersen等[4]使用有限元程序对吸力式筒基安装过程对周围土体抗剪强度的影响进行了研究；Zhou等[5]对筒基沉贯时筒外部土体流动机制进行了有限元分析，并研究了筒壁顶端形状效应对土体流动的影响，进而对土塞形成的影响；Zhang等[6]使用有限元方法对筒基安装过程中由于吸力所引起的土体渗流问题以及最大容许吸力进行了研究；Andersen等[7]使用有限元程序对吸力式筒基安装过程中筒壁顶端周围土体的变形进行了研究，并分析其可能是造成筒壁摩擦力减小的主要原因。在上述有限元模拟中，筒内负压如何施加将在很大程度上决定分析结果的准确性，由于缺乏更多试验数据进行验证，这方面问题还需要进一步的探讨。

由于筒基沉贯过程中土体会产生很大变形，在有限元模拟中将使表征土体的网格产生严重畸变，从而对模拟过程造成了一定的难度，针对这一问题，国内外学者使用了不同方法来解决。Vasquez等[8]应用有限元网格重划分技术，模拟了吸力筒自重沉贯和吸力沉贯过程，并将结果与物理试验进行对比；Zhou等[9]基于大变形有限元法使用了 AFENA软件研究了在正常固结黏土中吸力筒吸力式和压力式贯入的区别；Zeinoddini等[10]为避免网格畸变问题，在建立三维有限元模型时，采用假定筒壁贯入深度并预先建立筒壁贯入孔道的方法，对筒形基础压力式贯入过程进行了模拟，类似的方法也在韩智臣[11]的吸力式筒基安装过程有限元模拟中被采用；武科[12]在对负压沉贯引起的渗流场变化的研究中，通过建立筒壁生死单元的方法避免网格畸变问题，从而模拟了筒基下贯过程。由此可见，在使用有限元对吸力式筒基安装过程模拟中，还有尚待进一步改进和探讨的方面。

根据上述分析，本研究采用了大型有限元程序ABAQUS中的ALE（Arbitrary Lagrangian-Eulerian Formulation，任意拉格朗日-欧拉算法）技术，建立了吸力式筒形基础沉贯过程的轴对称模型，应用显示积分算法分析了黏土中筒基贯入过程。该方法也能够有效地解决由于土体大变形而产生的网格畸变问题，很好地预测了安装过程中筒基沉贯深度以及筒内土塞的高度。另外，基于ABAQUS程序VUFIELD[13]子程序二次开发模块，实现了黏土的力学强度随深度变化的特性，更加真实地反映了出土体的力学性质。通过将数值模拟结果与离心机试验进行对比，验证了数值模拟的准确性。最后进行了参数分析，获得的结论能够为吸力式筒基的设计和施工提供有价值的参考依据。

2 有限元模型

2.1 模型形式与尺寸

Chen等[14-15]利用西澳大学的臂式离心机分别对吸力筒的压力式贯入和吸力式贯入做了一系列离心机试验模拟。试验是在正常固结黏土中完成的。所用试验筒形及基本尺寸如图1所示，离心机加速度为120g，根据比尺效应，可计算得到原型尺寸。为了直接与离心机模型试验所对应的原型结果进行对比以验证数值模拟结果，建立等同于原型尺寸的数值模型，如图2所示，吸力筒直径d=3.6 m，筒高L=14.4 m，筒壁厚t=0.06 m。为消除边界效应，土体计算范围沿径向取7.5倍吸力筒直径，沿深度方向取10倍吸力筒直径。

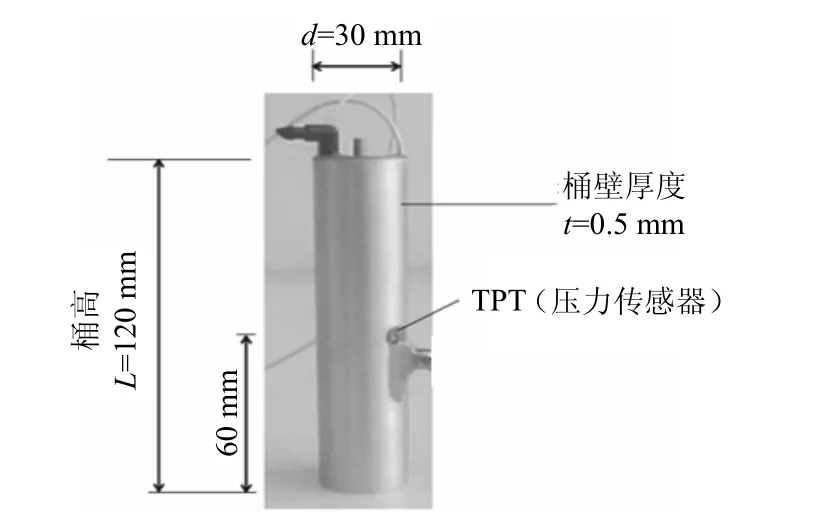
图1 离心机试验模型筒Fig.1 The geometry of suction bucket model in the centrifuge experiments

图2 有限元中土体和吸力筒大小Fig.2 Dimensions of the soil mass and suction bucket considered in the FE simulation

2.2 材料本构及参数选取

数值模型中，用理想刚体来模拟吸力筒壁，饱和黏土则使用理想弹塑性本构模型进行模拟，采用von Mises屈服准则。为了更加真实地模拟试验所用土体强度随深度变化这一特性，根据离心机试验中的T-bar测试结果[14-15]，本研究基于ABAQUS二次开发模块 VUFIELD[13]，编写了黏土抗剪强度随深度变化的子程序，结合本构模型来模拟黏土的应力-应变关系。子程序中采用由 T-bar测试获得的黏土不排水抗剪强度经拟合后得到的其随埋深z线性变化关系为

式中：z为埋深（m）；Su为不排水抗剪强度（kPa）。同样地，弹性模量 E= 375 + 480z （kPa）。土体的泊松比v=0.499，即近似不可压缩。初始应力状态根据土体浮重度γ=6.8 kN/m3以及水平土压力系数K0= 0.65计算得到[15]。

2.3 土-筒接触关系

吸力筒与土体的接触面采用 ABAQUS中的接触对算法（contact pair）[13]，通过定义的接触面相互作用力学传递模型来模拟界面的摩擦接触特性。接触面的法向模型采用“硬接触”，只有当两个接触面相互接触、压紧时才能传递法向压力，若两物体之间有间隙时不传递法向压力。接触面的切向行为采用基于罚刚度算法的Coulomb摩擦模型。该模型用摩擦系数μ来表征接触面之间的摩擦行为，在切向力达到一个临界剪切应力值之前，两面之间无明显的相对运动，其值可表示为

式中：τ为临界剪切应力；P为法向应力值。

2.4 ALE技术及模型网格划分

在吸力筒的贯入过程模拟中，土体会发生大变形，用常规的有限元方法进行分析时，表征土体的网格会产生严重的畸变，造成计算精度下降甚至计算中止。为了解决这一问题，本研究利用了 ALE技术，充分发挥结合了纯拉格朗日分析和纯欧拉分析的优点。一个完整的ALE分析包括3个步骤：①根据受力平衡，采用纯拉格朗日分析，获得土体变形；②由上一步的土体变形，运用ALE本身网格优化技术，在不改变拓扑形状和网格数目情况下，建立一个新网格体系；③采用欧拉分析算法，将第①步分析获得的结果以及材料点上状态变量映射到到新网格上[16]。通过这种做法，网格与物质点之间是可以相互脱离的，因而即使网格发生了很大的畸变，ALE方法也能使数值分析继续进行，并保证整个分析过程具有高质量的网格。

为提高有限元计算效率，只将土体可能发生明显大变形的区域定义为ALE区域，施加ALE技术，如图 3所示。土体的初始网格划分对之后的 ALE网格优化结果影响很大。由于吸力筒筒壁较薄，其贯入深度较大，为了保证在较高的计算效率下能够获得准确的分析结果，本研究通过尝试多个初始网格划分策略，最终采用长宽比为13:1的4节点轴对称缩减积分单元（CAX4R）[13]，将土体划分成16 500个单元。分析采用显示积分计算方法，根据网格的尺寸，计算时间步长 Δt = 1.0× 1.0-6s 。

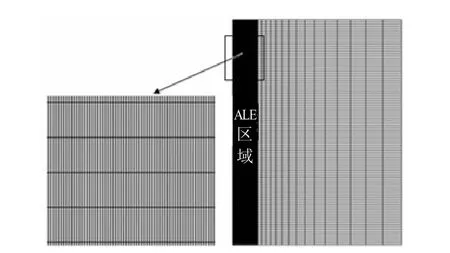
图3 网格划分情况及ALE区域Fig.3 Meshing and ALE domain

2.5 数值模拟沉贯过程

图4 沉贯过程模拟Fig.4 Simulation of penetration process

本文对吸力筒安装过程的模拟分为压力式贯入和吸力式贯入两种方法；两种方法都采用首先进行自重贯入，然后再进行压力或吸力式贯入两个阶段。如图4所示，参照离心机试验过程，首先以光滑加荷的方式对筒体施加竖向位移U，模拟完成自重贯入阶段（U=y1）。之后，在筒盖及筒内土体上表面施加均布荷载p、s，分别模拟筒体下贯压力与筒内土体表面吸力，并通过多个分析步，逐步增加荷载大小，沉贯深度逐渐增加，以筒内土塞到达筒顶盖为沉贯结束标准，完成整个吸力筒沉贯过程模拟，此时的p、s值即代表贯入完成所需的下贯压力与吸力大小。当保持s=p时，模拟过程为纯吸力式贯入；当保持s=0 kPa时，模拟过程为纯压力式贯入。

3 模型的验证

3.1 数值模拟与离心机试验对比

基于以上的模拟方法，本研究参照Chen等[14-15]的离心机试验，分别进行了压力式和吸力式贯入过程的数值模拟。数值模型中筒体沉贯结束时对应的应力位移云图见图5、6。

图5 压力式沉贯云图Fig.5 Nephogram of jacked penetration

试验表明，土体与筒壁摩擦系数是变化的[17]，筒壁周围土体细观结构、应力分布的变化和土体中水渗流作用、孔隙水压力变化等都影响摩擦系数的变化[18]。因此，在本文中，采取简化，通过直接改变筒壁-土体的摩擦系数来反映摩擦特性对沉贯阻力的影响。Vásquez等[8]根据其数值模型校准出的土筒摩擦系数为0.16，但与真实试验对比发现，该摩擦系数仍然较大，并考虑真实贯入过程中渗流对土筒接触的影响，因此，本研究中考虑土体与筒壁接触面的摩擦系数在0.04到0.10之间变化，并且假设土体与筒内外壁的摩擦系数相等。将数值模拟获得的沉贯阻力随着贯入深度变化的结果与Chen等[14-15]的离心机试验结果进行对比，如图7所示。

从图中可以看出，随着贯入深度的增加，筒体所受到的沉贯阻力也逐渐增加。无论采用何种贯入方式，数值模拟与试验结果均揭示了两个沉贯阶段的阻力随贯入深度变化的特点，即：自重贯入阶段，沉贯阻力随贯入深度呈现线性关系；压力或吸力贯入阶段，阻力随贯入深度呈现非线性关系。当采用吸力式贯入时，摩擦系数μ=0.08～0.10，模拟的结果与试验结果吻合得较好；而采用压力式贯入时，摩擦系数μ=0.06，模拟与试验较吻合。采用压力式贯入时，土体对筒壁的法向应力较吸力式贯入时要大，该现象可能导致在两种贯入方式下，筒壁与土体之间的摩擦性质存在一定的差异。总体来说，当选用合适的土体-筒壁摩擦系数时，模拟结果与离心机试验结果拟合得较好。

利用已校核好的摩擦系数，作压力式贯入（μ=0.06）与吸力式贯入（μ=0.08）数值模拟，将数值模拟所施加的荷载值与沉贯深度的关系与Chen等[14-15]的离心机试验结果进行对比，如图 8所示。注意，试验中吸力式贯入时所施加的吸力值略大于筒体所承受的总沉贯阻力。

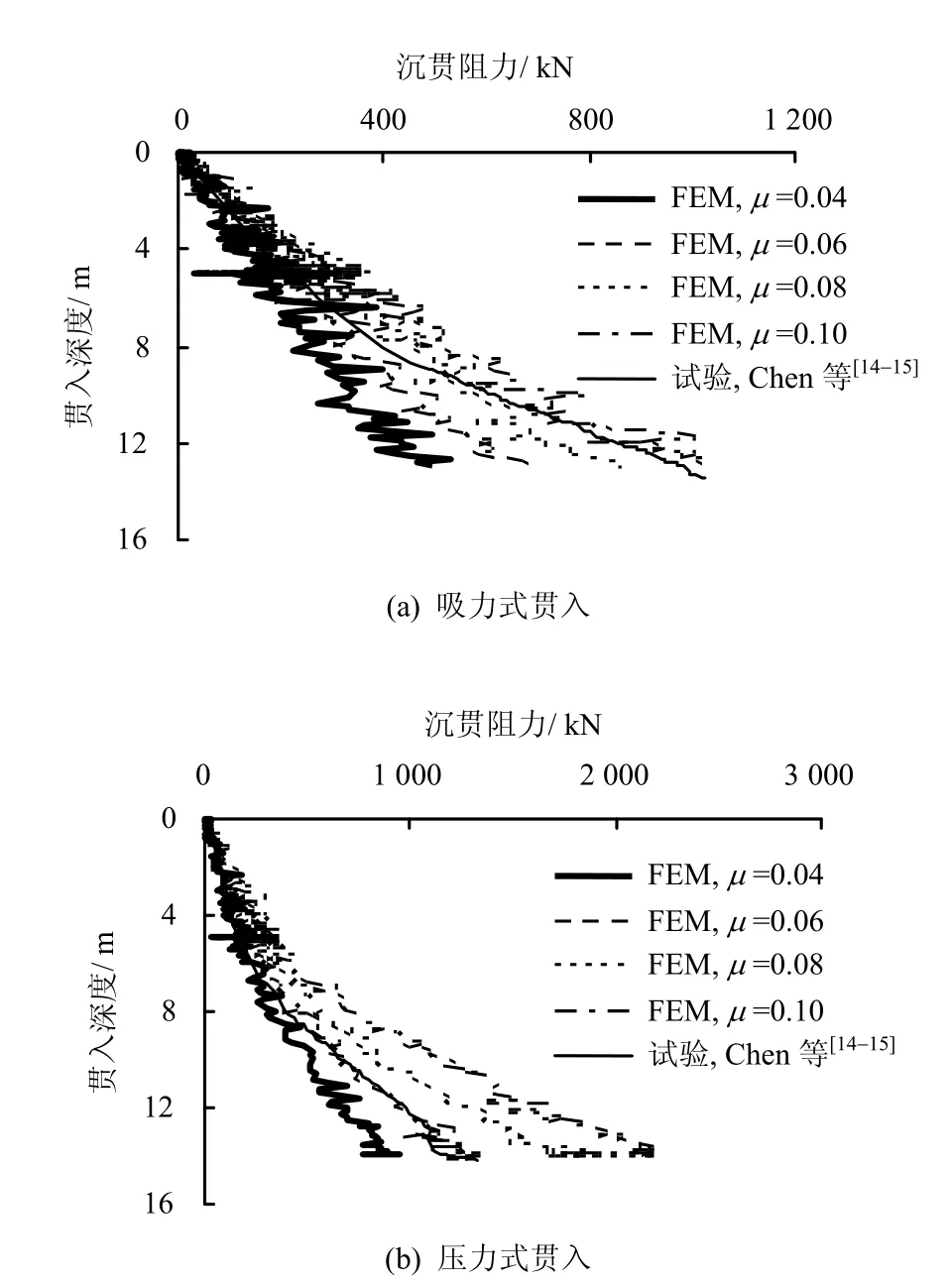
图7 沉贯阻力与贯入深度关系曲线（与试验对比）Fig.7 Variations of penetration resistance with depth(compared to test)

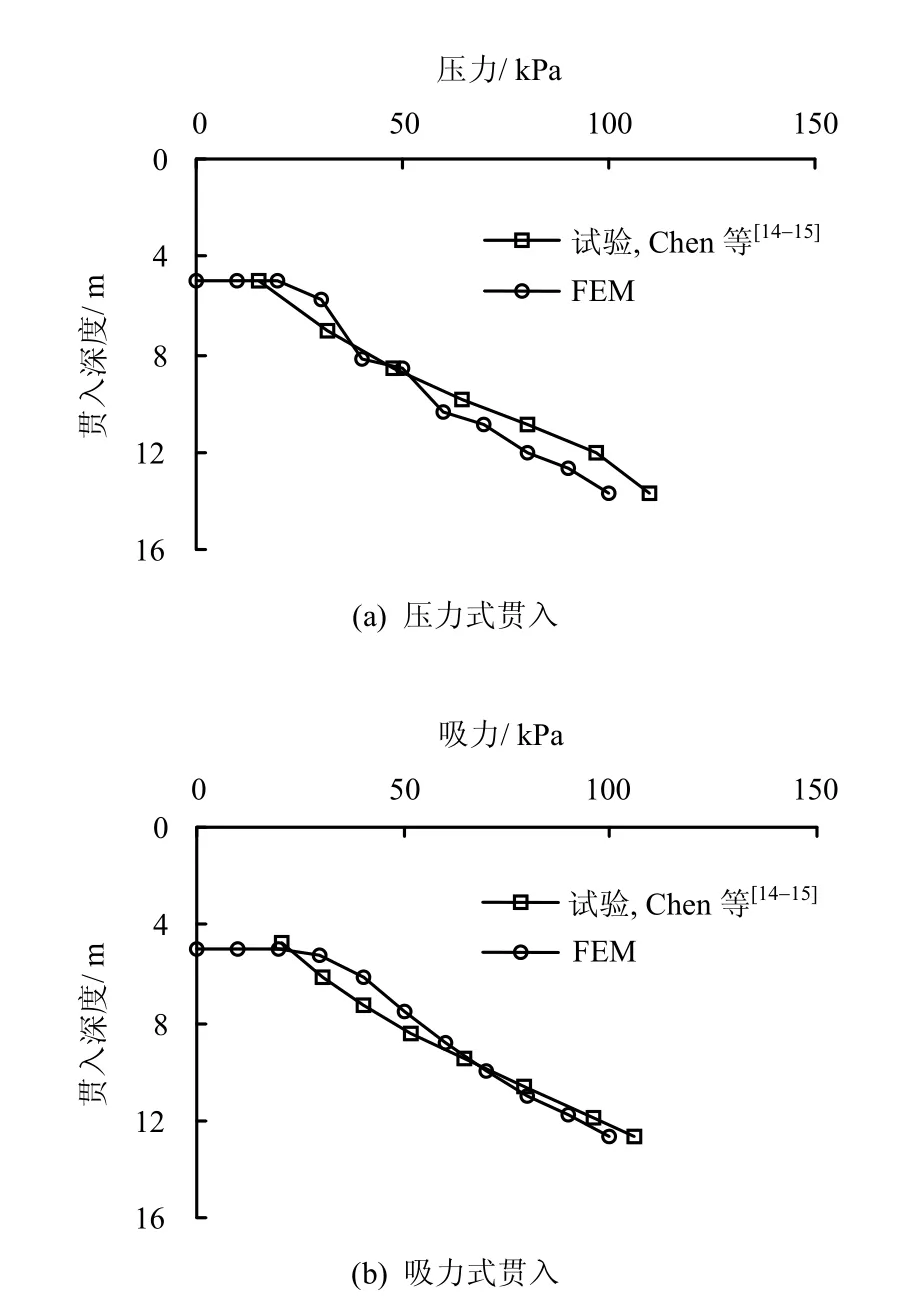
图8 吸力与贯入深度关系曲线Fig.8 Variation of suction with depth

从图8中可以看出，数值模拟中无论是压力式贯入所施加的下贯压力值还是吸力式贯入所施加的吸力值，随贯入深度的关系与试验结果拟合良好。这不仅说明了数值模拟很好地重现了真实模型试验，也说明采用合适的摩擦系数，通过逐级施加荷载的方法，可以预测出贯入到一定深度所需要的下贯压力和吸力值。

在Chen等[14-15]的离心机试验中，筒壁外侧设置了压力传感器，记录了吸力筒沉贯过程中该处法向应力值的变化。在本研究的数值模拟中，通过提取相应位置处的筒壁法向应力值，与离心机试验结果进行对比。图9表示在吸力式贯入下，筒壁法向应力随着贯入深度的变化曲线。值得注意的是在离心机试验中，筒壁的压力传感器在开始阶段（z＜zw）经历了静水压力作用，为了便于对比，数值模拟结果加上了对应深度的静水压力。如图9所示，筒壁法向应力随着贯入深度增加而增加，数值模拟的结果与试验数据十分吻合。

图9 吸力式贯入下筒壁压力与贯入深度变化曲线Fig.9 Variation of bucket wall pressure with depth under suction penetration condition

3.2 数值模拟与理论分析对比

Houlsby等[19]对黏土中吸力式筒形基础沉贯阻力进行了研究，通过土体极限平衡理论，获得的沉贯阻力解析表达式为

式中：V′为吸力筒自重；s为吸力大小；Di为筒内径；Do为筒外径；D为筒的平均直径；αi为筒内壁土体扰动系数；α0为筒外壁土体扰动系数；su1为贯入深度内的平均土体不排水抗剪强度；su2为筒端部的土体不排水抗剪强度；Nc为土体承载力系数；γ′为土的有效重度；h为贯入深度。

本研究将采用式（3）获得的沉贯阻力与数值模拟结果进行对比，进一步验证数值模拟的准确性。其中取筒尺寸参数、土体材料参数与数值模拟一致，参考Andersen等[20]的研究结果，取端部承载力系数Nc=7.5，筒内外壁土体扰动系数α均取为土敏感性系数的倒数，在 Chen等[14-15]的离心机试验中正常固结黏土的敏感性系数为2.8，因此，α取0.357。将吸力式贯入数值模拟结果与理论计算结果进行对比，如图10所示。同样地，当数值模拟取筒内外壁摩擦系数μ=0.08时，从图中可以看出，数值模拟与理论计算获得的沉贯阻力随贯入深度变化规律一致，结果比较吻合。

图10 吸力式贯入下沉贯阻力随贯入深度变化关系曲线（与理论对比）Fig.10 Variation of penetration resistance with depth under suction penetration condition(compared to theoretical results)

通过上述结果对比，可发现研究采用的有限元数值模拟能够较真实地重现物理试验和理论分析结果，对于压力式和吸力式两种不同的贯入方式，数值模拟结果与试验和理论计算结果较吻合，从而验证了所采用的数值模拟技术的有效性和准确性。

4 参数与结果分析

4.1 吸力大小的影响

吸力筒的总沉贯阻力主要由3部分组成：端部阻力、筒内壁摩阻力、筒外壁摩阻力[19]。为了进一步考察并预测沉贯阻力的大小，数值模拟分析不同吸力作用下，各部分阻力随贯入深度的变化关系。参考Chen等[14-15]的离心机试验，保证所施加的吸力在所要求的最大吸力范围之内[19]，分别采用最终吸力值为s=0、20、40、60 kPa（注意，由于此处施加的最终吸力值较纯吸力沉贯略小，为保证筒基下贯到最大深度，模拟的是吸力与压力同时施加的贯入过程，对应于上述吸力值，最终压力值分别为p=110、75、45、20 kPa），对吸力式贯入进行数值模拟，所获得的结果曲线如图11所示。从图中可看出，在不同吸力作用下，端部阻力、内壁摩阻和外壁摩阻都随着贯入深度的增加而增大；不同的是，3部分阻力随贯入深度增加的速率有所不同，即：随着施加的吸力逐渐减小，端部阻力与内壁摩阻力增加的速率逐渐增大，而外壁摩阻力的增加速率不随吸力的大小而变化。进一步从图 11(d)中可以看出，由这3部分阻力组成的总沉贯阻力，也是随着贯入深度的增加而增加，增加的速率随着吸力的减小而逐渐增大。从图11综合比较中可以看出，总沉贯阻力主要由内、外壁摩阻构成，而端部阻力占据较小的部分。另外，当所施加的吸力s=0 kPa时，等效于压力式贯入，从图中可看出当采用压力式贯入时，所需要克服的总沉贯阻力远大于吸力式贯入时的阻力。因此，采用吸力贯入方式可以有效地提高该类基础的安装效率和成本。上述数值分析得到的吸力对各部分沉贯阻力的影响与朱儒弟等[21]的室内模型试验结论一致。

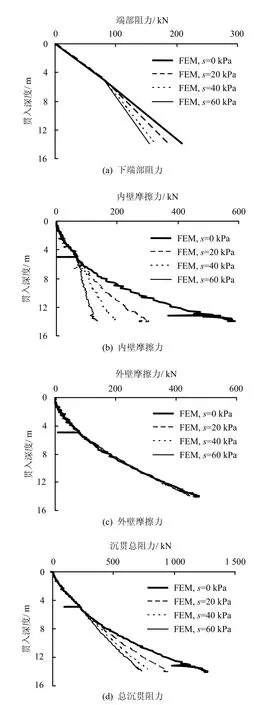
图18 不同吸力作用下总作用力随贯入深度变化关系曲线Fig.18 Variation of each stress with depth under different suctions

4.2 土塞高度变化规律分析

筒内土塞对吸力式基础最终沉贯深度影响较大。本研究考察了吸力沉贯时筒壁周围土体变形特点以及所引起的筒内土塞高度。在 ALE数值分析中，由于网格节点与物质点相互脱离，因而本研究采用ALE所特有的物质点跟踪技术（Tracer）[13]，实时考察代表土体的物质点的运移轨迹。

如图12所示，图中方形点代表跟踪的物质点，可以看到，随着沉贯开始进行（从T0向T3阶段进行），原本均匀分布在筒壁两侧的物质点，逐步随着筒壁向下运动，紧挨筒壁外侧的物质点逐渐绕过筒壁端部向筒内移动，从而使筒内土体体积迅速增加，引起筒内土体向上隆起，形成土塞。

数值模拟进一步考察了施加不同最终吸力s=0、40、60、80 kPa下，即贯入方式从纯压力式逐步向纯吸力式转化中，土塞高度随贯入深度变化的关系曲线。数值模拟中将筒内土体上表面高于筒外土体表面的距离提取作为土塞高度。

如图13所示，在自重贯入至4.95 m过程中，筒内土表面没有出现明显的变化，之后在继续进行吸力为0 kPa的压力式贯入时，筒内土体表面随着贯入深度的增加而呈现出一定的下降趋势。当采用吸力式贯入时，筒内土体表面表现出明显的隆起现象即土塞；当沉贯的吸力逐渐增加时，筒内土塞增长的速度也在增加，尤其在沉贯后期即沉贯深度大于12m时，s=80 kPa条件下要远大于s=40、60 kPa条件下形成的土塞高度，可能形成过大的土塞。该数值模拟获得的土塞高度随贯入深度的变化规律与国振等[22]的室内模型试验结果一致。

通过以上分析可以发现，虽然吸力式贯入较压力式贯入具有更小的沉贯阻力，但当采用吸力式贯入时，对施加吸力大小控制要特别注意，从抑制过大土塞形成的角度来看，吸力值不宜过大，应该根据实际工程的土质条件，控制在一定范围内。

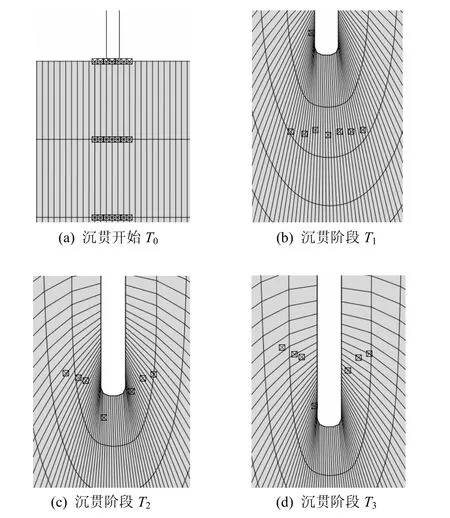
图12 筒端部附土体颗粒流动图Fig.12 The displacement of the soil particles around the bucket tip

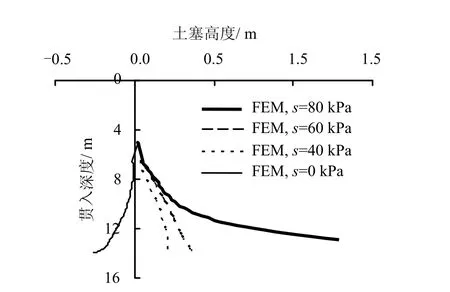
图13 土塞高度与贯入深度的关系曲线Fig.13 Soil plug heave versus penetration depth

4.3 筒内壁摩擦特性的影响

通过以上的模拟和分析结果，可以发现筒壁摩擦阻力以及所对应的筒壁-土之间的摩擦性质对沉贯阻力的预测有很大的影响；另外，考虑到筒壁法向上应力值对筒壁-土体之间的摩擦性质将产生很大的影响，本研究考察了筒内壁不同摩擦系数在吸力式和压力式贯入方式下对总沉贯阻力的影响。数值模型中外壁摩擦系数μ=0.08保持不变，取不同的内壁摩擦系数μ=0、0.05、0.10，分别模拟吸力式贯入和压力式贯入，所获得的结果如图 14～16所示。从图可以看出，相同的摩擦系数下，压力式贯入与吸式贯入最主要的区别在于内摩阻力的不同。对于吸力式贯入，贯入过程中由于筒内土体上部承受向上的吸力作用，使土体的竖直方向上的变形增加，而横向上呈现压缩变形，故对筒内壁的法向应力相对较小；而对于压力式贯入，由于下贯过程中筒内土体的侧向上发生较大的膨胀变形，土体对筒壁形成了被动土压力作用，进而对筒内壁的法向应力较大，因此，导致了压力式贯入筒壁内侧产生较大的摩擦阻力，从而使总沉贯阻力较吸力式贯入有显著的增加。另外，从图15可以发现，随着摩擦系数的增加，筒内壁法向压应力也在增加，因此，相应的摩擦阻力会有更显著的增加。图16表示不同摩擦系数下，总沉贯阻力的变化情况。可以看出，压力式贯入时，总沉贯阻力随摩擦系数增加而增加，增加的幅度较吸力式贯入要大。上述数值模拟分析得到的吸力式与压力式贯入的侧壁摩擦特性与El-Sherbiny[18]的模型试验结论相符。

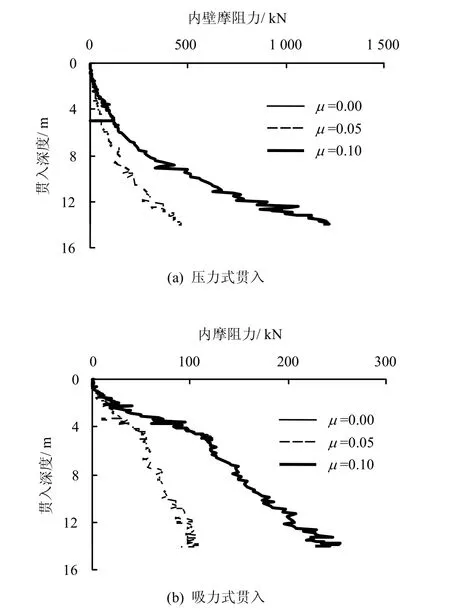
图14 内壁摩阻力与贯入深度的关系曲线Fig.14 Curves of internal bucket wall friction with penetration depth

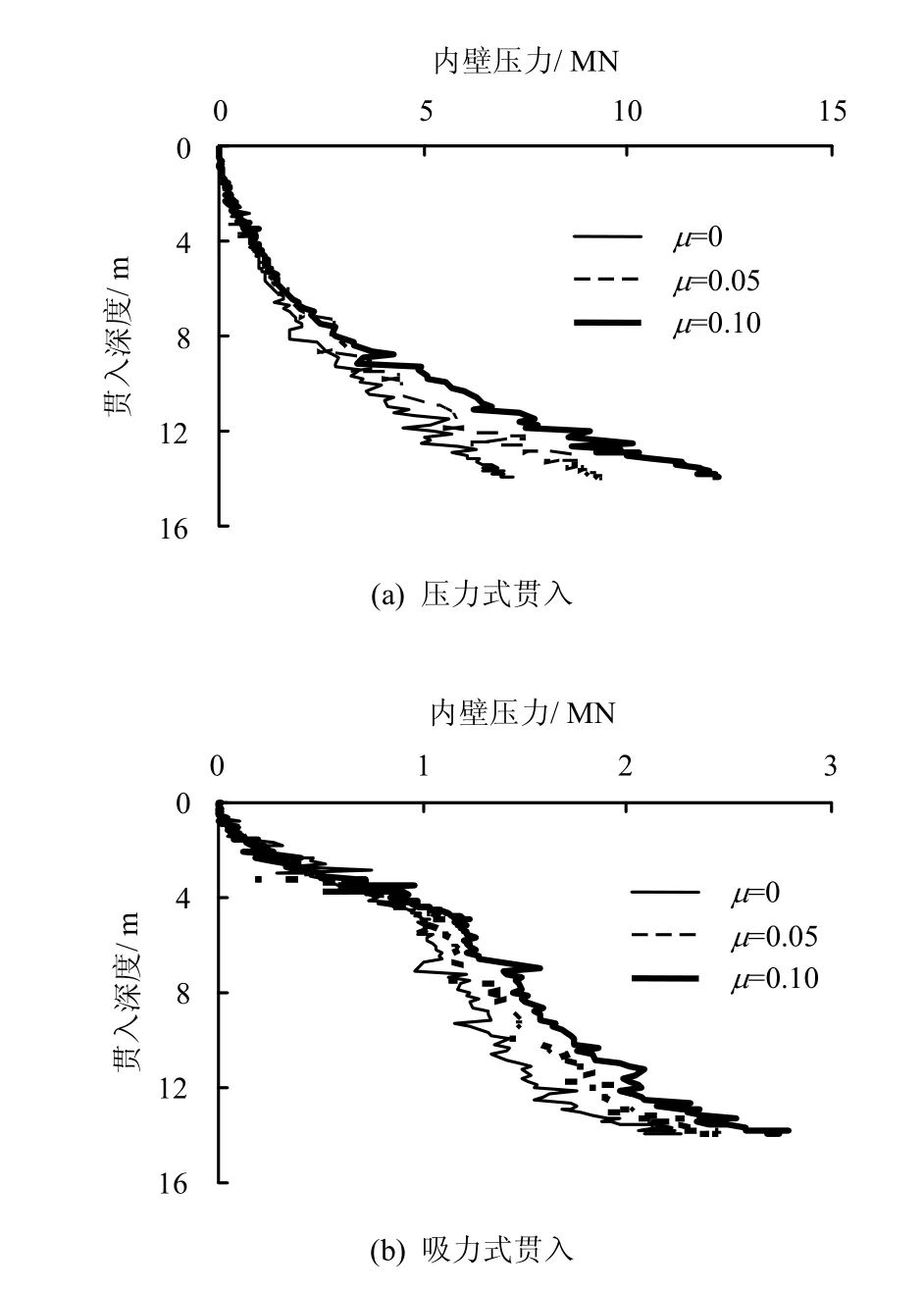
图15 内壁总压力与贯入深度的关系曲线Fig.15 Curves of total bucket wall pressure with penetration depth

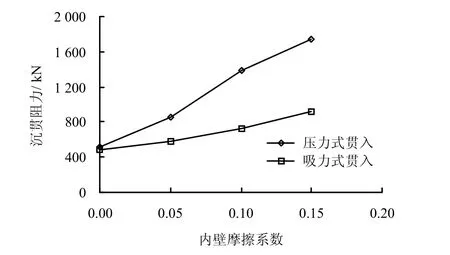
图16 内壁摩擦系数与沉贯阻力的关系曲线Fig.16 Curves of penetration resistance with internal bucket wall friction coefficient

通过以上分析，可对该类基础沉贯设计提供建议：吸力式贯入较压力式贯入高效，同时，对筒内壁的摩擦特性的敏感程度较低；当采用吸力式贯入时，可以通过刨光内壁、增强沿筒壁内侧渗流作用等途径来降低摩擦系数，从而降低沉贯阻力，提高安装效率。

5 结 论

（1）本研究所采用的ALE有限元模拟技术能够有效地解决由于土体大变形所引起的网格畸变问题，从而能够较真实地模拟吸力式筒形基础的沉贯过程；另外，基于ABAQUS程序VUFIELD子程序二次开发模块，研究了黏土的力学强度随深度变化的特性，更加真实地反映了出土体的力学性质，通过与物理试验和理论分析结果进行对比，验证了所建立的数值模型具有一定的有效性和准确性。

（2）使用所验证的数值模型对吸力式筒形基础的压力式沉贯和吸力式沉贯过程进行模拟，从施加的最终吸力大小、筒壁摩擦特性对贯入阻力的影响以及土塞高度的预测等方面进行了研究，获得了如下结论：

筒形基础贯入阻力主要由筒壁端部阻力、筒内壁摩擦阻力和外壁摩擦阻力3部分组成，而筒内、外壁摩擦阻力所占比例较大，而端部阻力所占比例较小。随着施加最终吸力值的增加，筒体沉贯阻力逐渐减小；当采用压力式贯入时（即s=0 kPa），所需要克服的总沉贯阻力远大于吸力式贯入时的阻力。

通过数值模型对筒壁-土体摩擦特性的考察发现，压力式贯入与吸式贯入最主要的区别在于筒内壁摩擦阻力的不同，压力式贯入产生的筒内壁摩擦阻力要高于吸力式贯入产生的内壁摩擦阻力，而筒外壁的摩阻力差异很小。针对该类基础，吸力式沉贯安装方式较压力式安装要高效。

当采用吸力式贯入时，对施加吸力大小控制要特别注意，从抑制过大土塞形成的角度来看，吸力值不宜过大，应该根据实际工程的土质条件，控制将吸力在一定范围内。

（3）由于本研究数值模拟中所采用的土体本构模型没有将土体的孔隙水压力及有效应力考虑进去，具有一定的局限性，所以在预测沉贯阻力、土体-筒壁摩擦特性及土塞高度等方面还存在一定的缺陷，有关方面问题将在今后研究中进一步探讨。

[1]李大勇, 张雨坤, 高玉峰, 等. 中粗砂中吸力锚的负压沉贯模型试验研究[J]. 岩土工程学报, 2012, 34(12):2277－2283.LI Da-yong, ZHANG Yu-kun, GAO Yu-feng, et al. Model tests on penetration of suction anchors in medium-coarse sand[J]. Chinese Journal of Geotechnical Engineering,2012, 34(12): 2277－2283.

[2]ZHANG P, DING H, LE C. Installation and removal records of field trials for two mooring dolphin platforms with three suction caissons[J]. Journal of Waterway,Port, Coastal, and Ocean Engineering, 2013, 139(6):502－517.

[3]刘晶磊, 王建华. 黏土中张紧式吸力锚破坏模式与承载特性有限元分析[J]. 海洋工程, 2013, 31(4): 10－20.LIU Jing-lei, WANG Jiang-hua. Numerical analysis of failure mode and bearing capacity of suction anchors with taut mooring systems in soft clay[J]. The Ocean Engineering, 2013, 31(4): 10－20.

[4]ANDERSEN K H, JOSTAD H P. Shear strength along outside wall of suction anchors in clay after installation[C]//Proceedings of the Twelfth International Offshore and Polar Engineering Conference. Kitakyushu,Japan: [s. n.], 2002.

[5]ZHOU H, RANDOLPH M F. Effect of caisson-tip geometry on flow pattern of soil plug[C]//Offshore Site Investigation and Geotechnics Confronting New Challenges and Sharing Knowledge, [S. l.]: [s. n.], 2007.

[6]ZHANG S, ZHENG Q, LIU X. Finite element analysis of suction penetration seepage field of bucket foundation platform with application to offshore oilfield developpment[J]. Ocean Engineering, 2004, 31(11): 1591－1599.

[7]ANDERSEN K H, ANDRESEN L, JOSTAD H P, et al.Effect of skirt-tip geometry on set-up outside suction anchors in soft clay[C]//ASME 2004 23rd International Conference on Offshore Mechanics and Arctic Engineering. [S. l.]: American Society of Mechanical Engineers, 2004: 1035－1044.

[8]VÁSQUEZ L F G, MANIAR D R, TASSOULAS J L.Installation and axial pullout of suction caissons:numerical modeling[J]. Journal of Geotechnical and Geoenvironmental Engineering, 2010, 136(8): 1137－1147.

[9]ZHOU H, RANDOLPH M F. Large deformation analysis of suction caisson installation in clay[J]. Geotechnique,2006, 43(12): 1344－1357.

[10]ZEINODDINI M, MOUSAVI S A, ABDI M R.Simulation of suction caisson penetration in seabed using an adaptive mesh technique[J]. Procedia Engineering,2011, 14: 1721－1728.

[11]韩智臣. 吸力锚的有限元数值分析[D]. 大连: 大连理工大学, 2013.HAN Zhi-cheng. Finite Element Analysis of Suction Anchors[D]. Dalian: Dalian University of Technology,2013.

[12]武科. 滩海吸力式筒形基础承载力特性研究[D]. 大连:大连理工大学, 2007.WU Ke. A study on bearing capacity behavior of suction bucket foundation in beach–shallow sea[D]. Dalian:Dalian University of Technology, 2007.

[13]SIMULIA. Abaqus Analysis: User’s Manual[M]. [S. l.]:Dassault Systèmes, 2012.

[14]CHEN W, RANDOLPH M F. External radial stress changes and axial capacity for suction caissons in soft clay[J]. Geotechnique, 2007, 57(6): 499－511.

[15]CHEN W, ZHOU H, RANDOLPH M F. Effect of installation method on external shaft friction of caissons in soft clay[J]. Geotechnique, 2009, 135: 605－615.

[16]KHOEI A R, ANAHID M, SHAHIM K. An extended arbitrary Lagrangian–Eulerian finite element method for large deformation of solid mechanics[J]. Finite Elements in Analysis and Design, 2008, 44(6): 401－416.

[17]PEDERSEN R C, OLSON R E, RAUCH A F. Shear and interface strength of clay at very low effective stress[J].ASTM Geotechnical Testing Journal, 2003, 26(1): 71－78.

[18]EL-SHERBINY R M. Performance of suction anchors in normally consolidated clay[D]. Houston: The University of Texas at Austin, 2005.

[19]HOULSBY G T, BYRNE B W. Design procedures for installation of suction caissons in clay and other materials[J]. Geotechnical Engineering, 2005, 158(2):75－82.

[20]ANDERSEN K H, JOSTAD H P. Foundation design of skirted foundations and anchors in clay[C]//Offshore Technology Conferences. Houston, Texas: [s. n.], 1999:383－392.

[21]朱儒弟, 高恒庆, 马小兵, 等. 海上平台桶形基础模型压力压贯与负压沉贯试验研究[J]. 海岸工程, 1999,18(1): 60－66.ZHU Ru-di, GAO Heng-qing, MA Xiao-bing, et al. The model experiment studies of model’s press penetration and suction penetration of bucket foundation of on the platform in the sea[J]. Coastal Engineering, 1999, 18(1):60－66.

[22]国振, 王立忠, 袁峰. 黏土中吸力锚沉贯阻力与土塞形成试验研究[J]. 海洋工程, 2011, 29(1): 9－17.GUO Zhen, WANG Li-zhong, YUAN Feng. An experimental investigation of insertion resistance and soil heave during caisson installat ion in soft clay[J]. The Ocean Engineering, 2011, 29(1): 9－17.