动载作用下岩石类材料破坏模式及能量特性

赵光明 ，马文伟，孟祥瑞

（1.安徽理工大学 煤矿安全高效开采省部共建教育部重点实验室，安徽 淮南 232001；

2.安徽理工大学 能源与安全学院，安徽 淮南 232001；3.煤科集团沈阳研究院有限公司，辽宁 沈阳 110015）

1 引 言

动载作用下，岩石类材料的强度特性、破坏模式和能量特性一直是岩石力学与工程界的重要课题。近几十年来，学者们对岩石类材料在高应变率下的强度特性研究颇多[1-5]，但由于试验设备及技术的限制，对试件破坏模式及能量特性研究比较少。对破坏模式的研究，通常只是通过大量的冲击试验，观察试件破坏后的特点，通过试件破坏表象来确定不同应变率下的破坏模式。近年来利用高速摄影技术结合数值散斑法发展了光学动态变形测试技术，用来研究岩石的破坏过程。李海波等[6]通过岩石动态压缩试验认为，单轴准动载荷作用情况下岩样呈锥型破坏模式，三轴情况下岩样呈剪切破坏模式；单仁亮[7]中利用SHPB装置对大理岩和花岗岩做了大量的冲击试验，总结出岩石的冲击破坏主要有压剪破坏、拉应力破坏、张应变破坏和卸载破坏，而且认为岩石的破坏总是有两种或两种以上的破坏形式同时发生，这与岩石本身的物理性质、内部的各种微结构、微裂纹的分布有直接的关系；陈庆寿等[8]通过对9种岩石进行动载冲击试验，将破坏模式分成3类：产生裂隙、中等程度破坏和强烈破碎；翟越等[9]对花岗岩和混凝土试件在冲击载荷作用下的破碎程度及破碎形式进行研究，混凝土试件在较低应变率下呈劈裂破坏的模式，在高应变率下大多呈现压碎破坏模式，而花岗岩试件在各应变率下的破坏模式为轴向劈裂拉伸破坏模式。在能量特性研究方面，夏昌敬等[10]利用SHPB装置冲击不同孔隙率的人造岩得出，在相同的冲击速度下岩石耗散的能量随着岩石孔隙率的增加而增加，岩石临界破坏所耗散的能量随着孔隙率的增加而减小；谢和平等[11]认为，在大体相同的应力-应变曲线下，试件的破坏形式不同，能量释放量完全不同；Zhang等[12]利用数字图像技术结合高速摄影测量岩石试件的表面变形特性，应用电子显微镜成像技术观察试件裂纹的脆性破坏，这些技术也能够应用于试件破坏模式的研究，但其试验设备相对昂贵，应用计算机数值模拟可以对试验进行一个很好的补充，借助于计算机数值模拟，很容易观测到岩石在冲击载荷作用下破坏的全过程、应力波在岩石内部的传播过程等等，同时也可以很方便地研究岩石的应变率效应及尺寸效应[13-15]。

本文以砂岩和混凝土试件在不同冲击速度下的SHPB试验为基础，通过应用ANSYS/LS_DYNA数值模拟软件模拟整个冲击过程，分析岩石试件的破坏模式，探索其在破坏过程中的能量特性，从而可以为工程实践做一些指导作用。

2 数值模型的建立及有效性验证

2.1 数值模型的建立

依据实际试验设备，应用 ANSYS建立整个SHPB试验系统，其中子弹的直径为14.5 mm，长度为 185 mm；入射杆为直锥变截面压杆，变截面段长度为30 mm，大端直径为30 mm，小端直径为15 mm，总长度为 1 000 mm；透射杆的直径为30 mm，长度为600 mm，子弹和杆件的弹性模量为210 GPa，泊松比为 0.3，密度为 7.8 g/cm3，如图 1(a)、(b)所示。为了提高计算精度，岩石试件

采用精细网格划分，共划分了11 520个网格，如图1(c)所示。模型中子弹划分3 456个单元，入射杆划分17 280个单元，透射杆划分11 520个单元。

图1 SHPB及试件有限元模型Fig.1 The finite element model of SHPB and specimen

子弹及压杆只会产生弹性变形，本构模型直接采用弹性模型；试件会产生大变形及与应变率相关的破坏模式，所以采用HJC模型，此模型是一种率相关损伤型本构模型，能够反映混凝土、岩石等脆性材料在大变形、高应变率和高围压下材料损伤失效动态响应。根据张凤国等[16]所研究的模型参数计算方法，得到试件的模型具体参数如表1所示。表中21个参数，强度参数包括：A、B、C、N、SFMAX，其中A为标准化内聚力强度、B为标准化压力硬化系数、C为应变率系数、N为压力硬化系数、SFMAX为材料所能达到的最大标准化强度；损伤参数包括：D1、D2，为损伤常数、EFMIN为材料最小塑性应变；压力参数包括：Pc、μc、Pl、μ1、T、K1、K2、K3，其中Pc和μc分别是单轴压缩试验时材料的压碎体积压力和压碎体积应变、Pl为压实压力，μ1为压实体积应变，T为材料最大拉伸应力，K1、K2和 K3为常数；以及参考应变率EPS0和失效类型fs。

表1 试件HJC本构模型材料参数Table 1 Material parameters of HJC constitutive model

2.2 模型有效性验证

为了说明所建模型的有效性，对比不同冲击速度下试验所得入射波、反射波以及透射波曲线与数值模拟所得相应曲线，如图2所示，由图可见，在相同的冲击速度下，试验所得的入射波、反射波波形与数值模拟所得的相应波形相吻合，对于透射波形，在波形的前半段，数值模拟结果与试验结果吻合度很好，在波形后半段，由于在数值模拟过程中，岩石试件单元失效后会自动删除，导致试件后续受力情况与实际受力情况有些不符，数值模拟所得透射波形曲线后半段与试验所得稍有出入，基于此，可以认为，此模型在模拟试样破坏过程上是可信的。

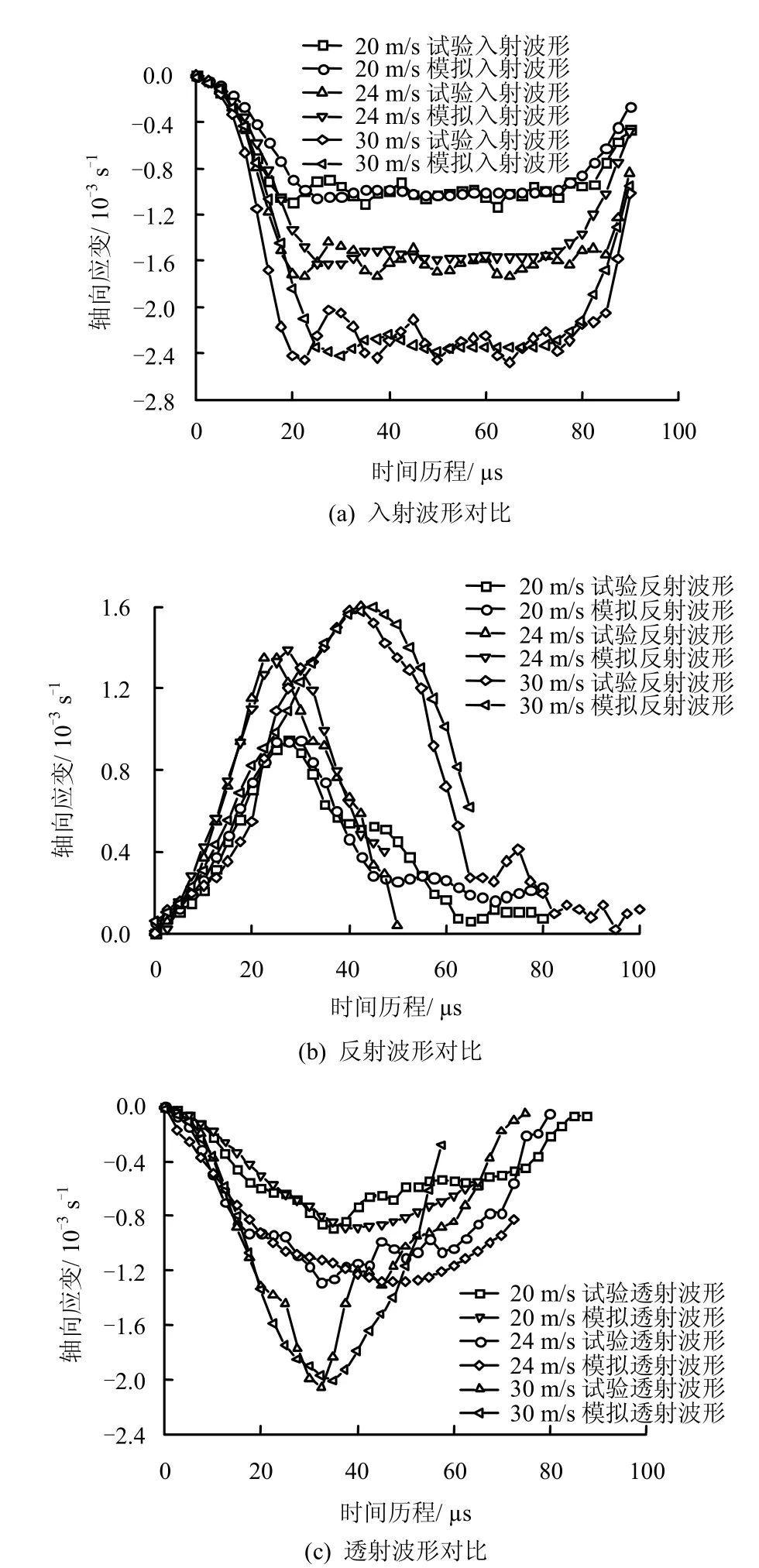
图2 试验波形曲线与模拟波形曲线对比Fig.2 Comparison of experimental wave curve and simulating curve

3 岩石破坏模式数值分析

为了分析岩石的破坏过程及破坏模式的发展历程，通过数值模拟将应力波在岩石中的传播分为4个阶段，第1阶段为试件破坏前应力波在岩石中来回反射，达到应力均匀阶段；第2阶段为试件产生张应变破坏阶段；第3阶段为试件由张应变破坏向轴向劈裂拉伸破坏转变阶段；第4阶段为试件向压碎破坏转变阶段。

图3所示为第1阶段，即试件破坏前应力波在试件内部传播的有效应力云图及其内部切片。图3(a)所示为应力波到达入射杆与试件的接触端后，应力波均匀地作用于岩石试件表面，由于存在边界效应，试件端面边缘处会出现较大的有效应力；随着应力波在岩石内部的传播，试件端面所受的有效应力在不断增大；应力波传播到透射杆端，发生发射现象，由图 3(c)～3(d)的变化过程可见，岩石试件透射杆端面的有效应力由边缘向内部扩展，之后随着应力波的继续传播，岩石透射杆端面各处有效应力趋于相同，如图 3(e)所示；随着应力波的继续传播，岩石试件内部各处有效应力基本趋于相同，可以认为试件达到应力均匀，如图 3(f)所示。在此阶段内，入射波一直处于上升，并没有达到应力波峰值。

应力波在岩石内部传播，在应力均匀后，随着入射应力波幅值的增大，试件内部的有效应力值也在不断增大，由于试件存在边界效应，两个端面外沿处的有效应力值最大，率先达到岩石试件所允许的最大有效应力，将首先发生破坏，之后，破坏将向试件外沿面中部和内部同时扩展，宏观表现为试件沿着周长剥去一圈，此即为岩石试件破坏的第 2阶段——张应变破坏阶段，破坏模式称为张应变破坏模式。此阶段的有效应力云图变化如图4所示。

在张应变破坏阶段，岩石试件将沿着周长剥去一圈，形成不规则的圆周表面，随着应力波在试件内部的传播继续增大，其有效应力将在试件内部和表面形成复杂的分布形式，试件将沿着轴向产生裂隙，并逐渐贯通上下表面，形成沿轴向破坏的较大块体，此即为试件破坏的第3阶段，如图5(a)、5(b)所示。最后的破坏模式称为轴向劈裂拉伸破坏模式。

如果冲击速度较大，试件发生轴向劈裂拉伸破坏后，随着传入岩石内部的应力波地继续增大传播，岩石试件将会被压碎成块度比较小、数量比较多的小碎块，呈现显著的压碎破坏，此即为试件破坏的第4阶段，称破坏模式为压碎破坏模式，如图5(c)所示。

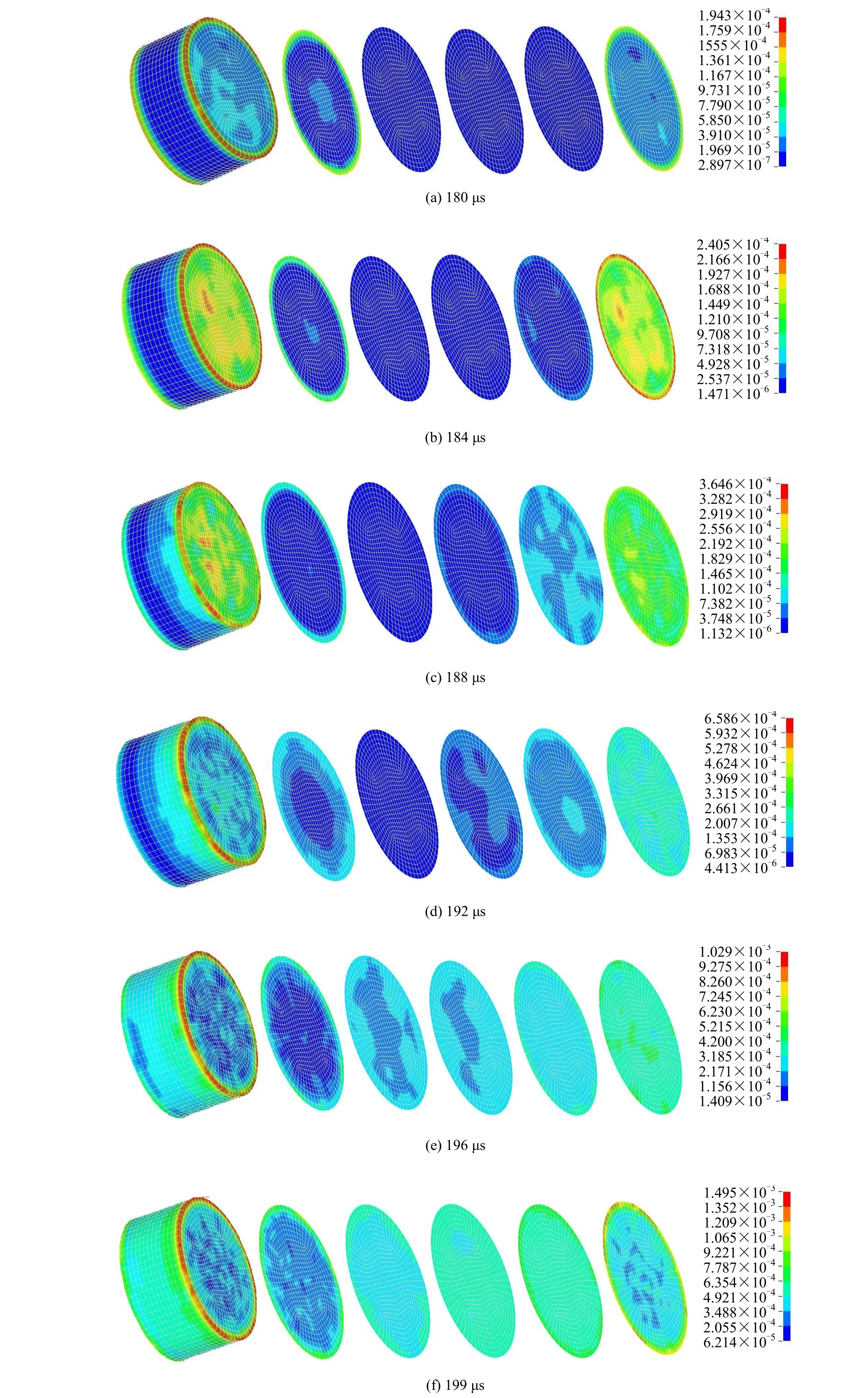
图3 不同时刻试件内部有效应力分布（单位：100 GPa）Fig.3 The effective stress distribution inside the specimen at different moments (unit: 100 GPa)

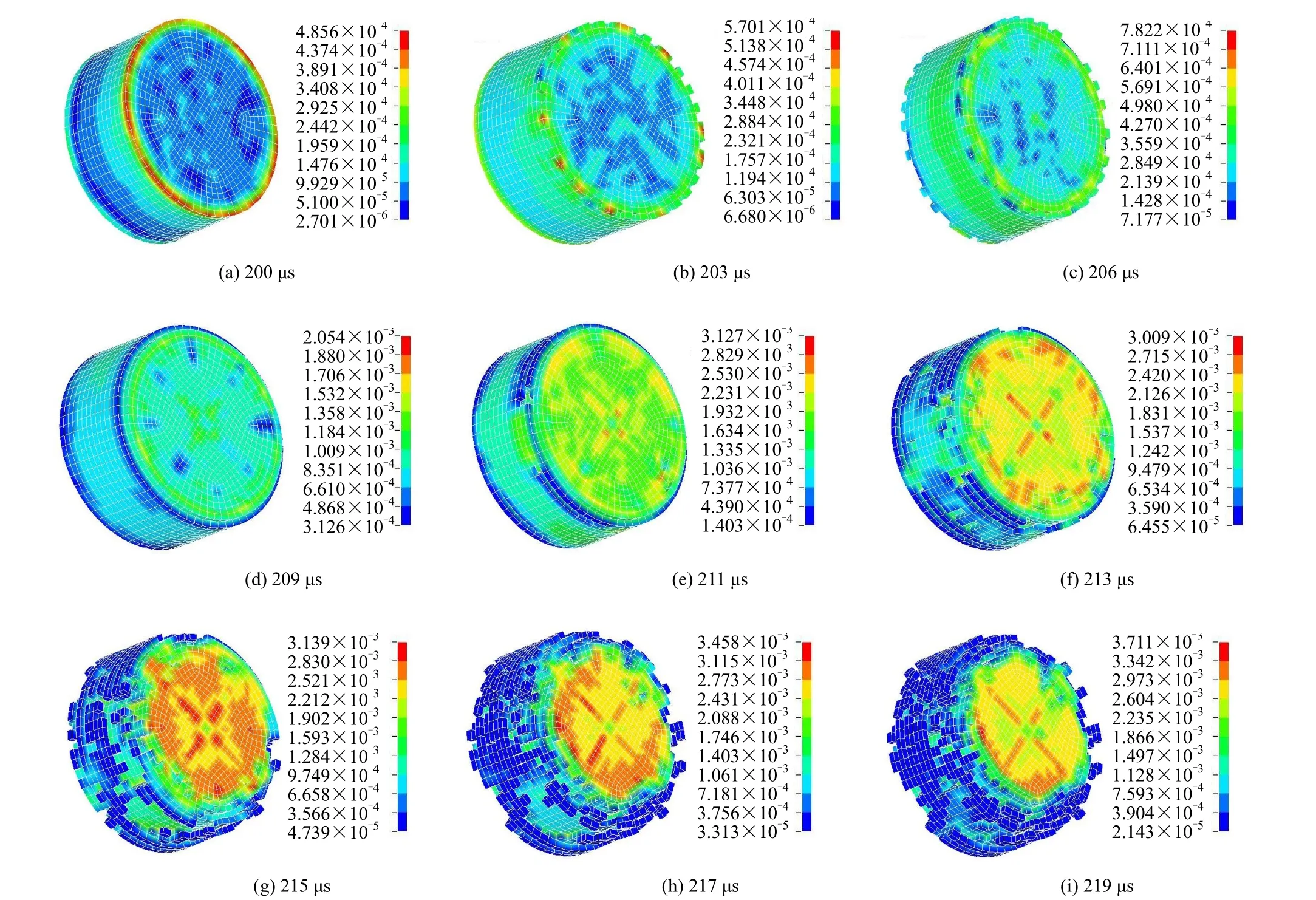
图4 张应变破坏阶段有效应力云图（单位：100 GPa）Fig.4 Nephograms of effective stress distribution within strain damage stage (unit: 100 GPa )

由以上4个阶段的分析可知，当冲击速度很低时，入射应力波达到峰值时，冲击强度仍没达到试件的破坏强度，此时试件不发生任何破坏；当冲击速度较低时，试件在完成第1阶段后，入射应力波还没有达到峰值，随着入射应力波强度的增加，试件开始发生张应变破坏，当入射应力波达到峰值时，试件仍处于第2阶段，此时试件只会发生张应变破坏，属于单一的张应变破坏模式；当冲击速度较高时，试件在完成第2阶段后，入射应力波仍没达到峰值，随着应力波的继续增加，试件轴向开始发生劈裂拉伸破坏，当应力波达到峰值时，试件仍处于第3阶段，此时试件产生的破坏形态是张应变破坏和轴向劈裂拉伸破坏共同作用的结果；当冲击速度很高时，试件在完成第3阶段时，入射应力波仍没达到峰值，随着应力波的继续增大，试件将被压成很小的碎块，形成压碎破坏模式。

对比试件最终的试验破坏形态及数值模拟破坏形态，如图6所示。张应变破坏宏观表现为试件沿着圆周剥去一圈，如图 6(a)所示；轴向劈裂拉伸破坏最终表现为试件沿轴向劈裂破坏成块体，块体高度大致与试件高度相当，如图6(b)所示；压碎破坏模式宏观表现为试件被压碎破坏成很小的块体，如图6(c)所示。

4 岩石试件能量相关性分析

在SHPB冲击试验中，系统必须满足2个基本假定：一维和均匀性假定。其中一维假定忽略了杆件中的横向惯性效应，所以当子弹以一定的动能作用于入射杆，不考虑放热损失，此动能将转化为入射杆中的入射能，随着应力波的传播，入射能转化为反射能、透射能及试件吸收能。试件吸收能将最终转化成试件中产生的弹性波能量，产生碎块新表面积及新裂纹的能量，试件的纵向与横向动能，以及试件声发射和发热等所产生的能量。

入射能可以代表系统提供的初始能量，透射能可以表征系统经过冲击后的剩余能量，研究这两者之间的关系，可以分析试件在冲击过程中的一些能量相关性。图7所示为不同应变率下入射能与透射能之间的关系曲线。

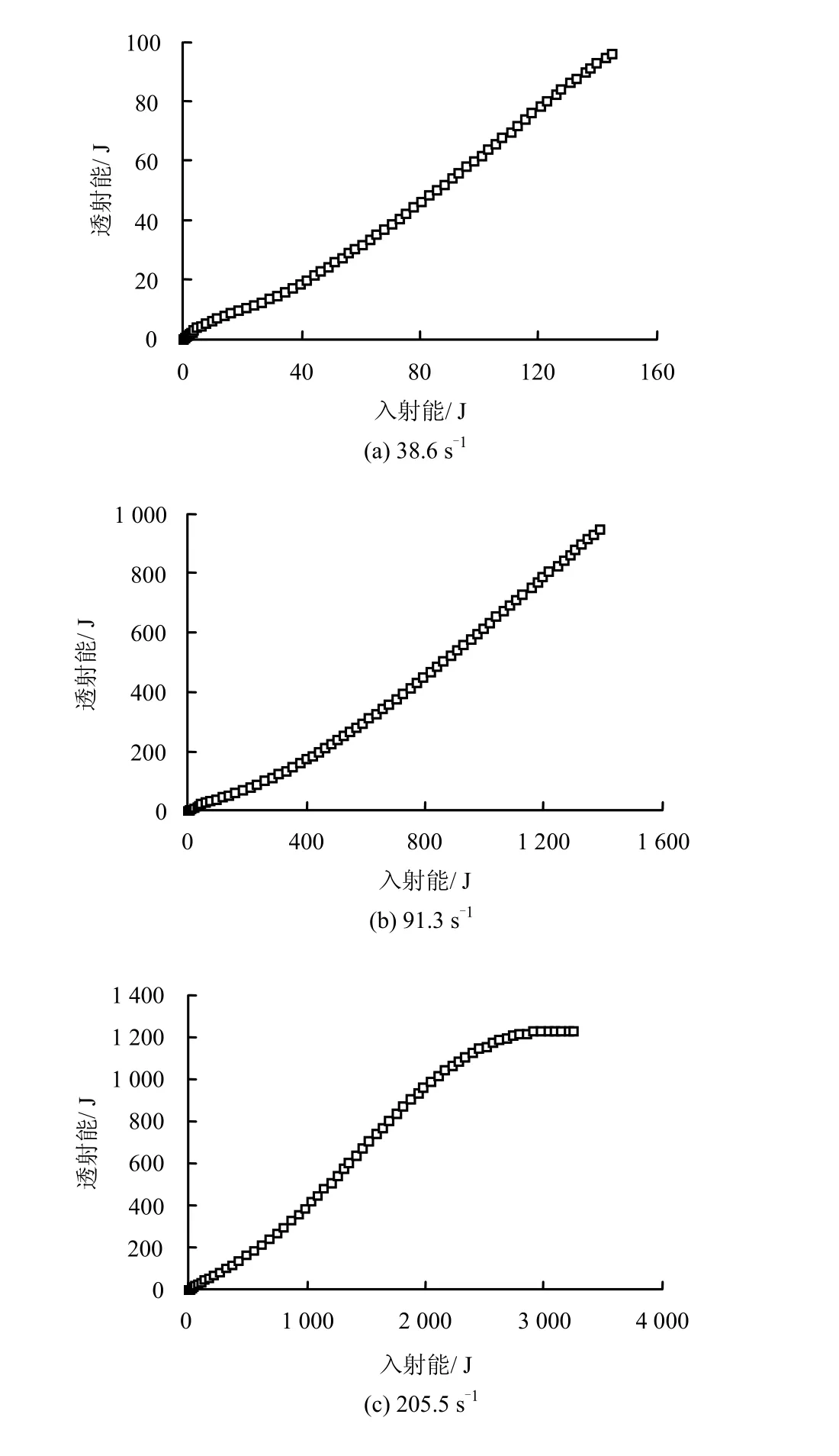
图7 不同应变率下入射能与透射能关系Fig.7 Relationship between incident energy and transmitted energy at different strain rates

由图可见，当应变率较低时，同时入射能也较低，此时透射能随着入射能的增大呈线性增长；当应变率较高时，在其入射能较低的阶段，透射能随着入射能的增加而线性增大，在入射能较大的阶段，随着入射能的增加，透射能也在增加，但增加幅度减缓，这是由于入射能的一部分能量被试件所吸收造成的，在入射能很大的阶段，透射能的增量已经变得非常小了，此时入射能的增加量主要被试件所吸收。这与李夕兵等[17]对大理岩和花岗岩等岩石所做冲击试验的结果是类似的。

对于试件来说，在其受动载作用过程中，逐步将入射能提供的能量转化为自身的内能。内能的变化规律与岩石的破坏有着直接的关系。图8所示为数值模拟中不同应变率下岩石试件内能的时间历程曲线。

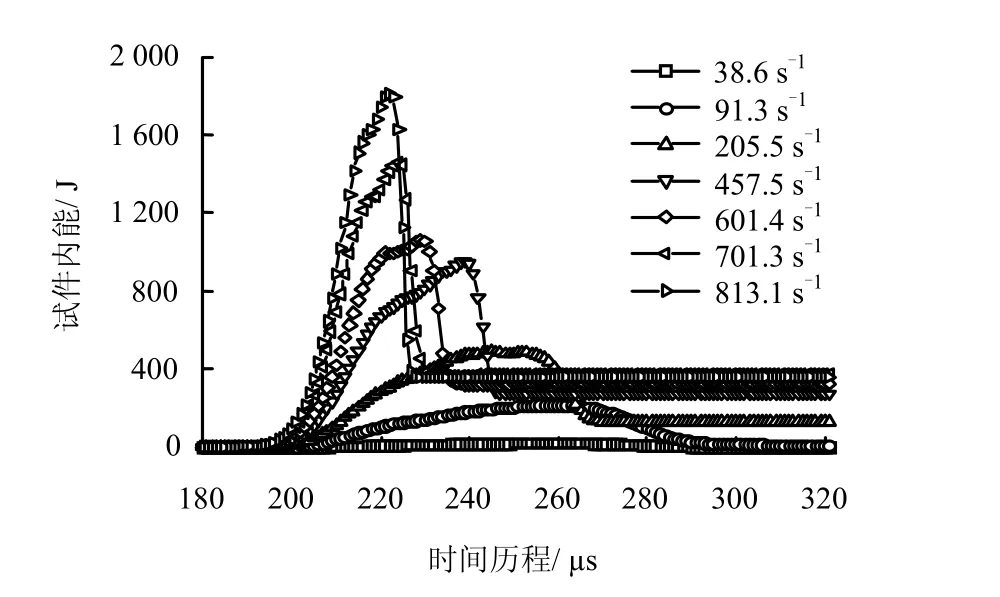
图8 不同应变率下试件内能-时间历程曲线Fig.8 Internal energy time history curve of specimen at different strain rates

通过分析图8可以得出，在低应变率下，试件没有发生破坏时，试件内能的变化分为两个阶段，如图中应变率为38.6、91.3 s-1曲线所示。第1阶段对应于试件的弹性压缩变形阶段，此时，试件的内能随着时间的变化呈线性增加；第2阶段为内能达到最大值后，试件没有发生破坏，试件处于弹性变形恢复阶段，内能全部消耗在试件的恢复变形上，此时试件的内能随着时间的变化逐渐降低，最后减小到0。

在较高的应变率下，试件发生不同程度的破坏，此时试件内能的变化可以划分为4个阶段。第1阶段对应于试件的弹性变形阶段，内能随着时间的增大线性增加；第2阶段对应于试件的塑性变形阶段，此时内能随着时间的增大也在增加，但增加幅度低于第1阶段；第3阶段为内能达到最大值之后，试件会发生破坏，包括产生新的裂隙，压碎石块的抛掷，消耗了一部分的内能，使内能发生较大程度的降低；第4阶段中内能为一个定值，称为残余内能，此内能值可以用来表征岩石试件在抛掷破坏后剩余部分的能量。

通过分析图8还可以得到，试件的内能值具有显著的应变率效应和时间效应。这是由于在入射应力波传播时，应变率越高，入射波达到相同峰值所用的时间越短，如图2(a)所示，而且在试件破坏前，入射能主要转化为试件的内能，加之试件的内能可以表征其动态强度，可以得出，应变率越高，试件的极限内能值越大，而且达到极限内能值所用的时间越短。

5 结 论

（1）岩石类材料在动载作用下的破坏可以分为3种模式：张应变破坏模式、轴向劈裂拉伸破坏模式和压碎破坏模式。随着应变率的提高，试件的破坏模式由张应变破坏模式向轴向劈裂拉伸破坏模式转变，再向压碎破坏模式转变。

（2）当应变率较低时，透射能随着入射能的增大呈线性增长；当应变率较高时，在其入射能较低的阶段，透射能随着入射能的增加而线性增大，在入射能较大的阶段，透射能随着入射能的增加缓慢增大，在入射能很大的阶段，透射能随着入射能的增加增量非常小。

（3）在低应变率下，试件不发生破坏，其内能随着时间的增加呈线性增加，一定时间后内能值逐渐降低到0；高应变率下，试件发生不同程度破坏，其内能值随时间的变化规律对应于试件的弹性变形阶段、塑性变形阶段、裂隙扩展碎块抛掷阶段和残余内能阶段。

（4）在冲击过程中，试件的极限内能值具有显著的应变率效应及时间效应。

[1]黄理兴. 岩石动力学研究成就与趋势[J]. 岩土力学,2011, 32(10): 2889－2990.HUANG Li-xing. Development and new achievements of rock dynamics in China[J]. Rock and Soil Mechanics,2011, 32(10): 2889－2990.

[2]宫凤强, 陆道辉, 李夕兵, 等. 不同应变率下砂岩动态强度准则的试验研究[J]. 岩土力学, 2013, 24(9): 2433－2441.GONG Feng-qiang, LU Dao-hui, LI Xi-bing, et al.Experimental research of sandstone dynamic strength criterion under different strain rates[J]. Rock and Soil Mechanics, 2013, 24(9): 2433－2441.

[3]FRIEDMAN M, PERKINS R D, GREEN S J.Observation of brittle-deformation features at the maximum stress of westly granite and solenhofen limestone[J]. International Journal of Rock Mechanics and Mining Sciences, 1970, 7: 297－306.

[4]OLSSON W A. The compressive strength of tuff as a function of strain rate from 10-6to 103/sec[J].International Journal of Rock Mechanics and Mining Sciences, 1991, 24(3): 231－250.

[5]平琦, 马芹永, 张经双, 等. 高应变率下砂岩动态拉伸性能 SHPB试验与分析[J]. 岩石力学与工学报, 2012,31(增刊 1): 3363－3368.PING Qi, MA Qin-yong, ZHANG Jing-shuang, et al.SHPB test and analysis of dynamic tensile performance of sandstone under high strain rate[J]. Chinese Journal of Rock Mechanics and Engineering, 2013, 31(Supp.1):3363－3368.

[6]李海波, 赵坚, 李俊如, 等. 花岗岩动态压缩力学特性的实验以及理论研究[J]. 辽宁工程技术大学学报, 2001,20(4): 474－477.LI Hai-bo, ZHAO Jian, LI Jun-ru, et al. Experimental and theoretical study on dynamic compressive mechanical properties of a granite[J]. Journal of Liaoning Technical University, 2001, 20(4): 474－477.

[7]单仁亮. 岩石冲击破坏力学模型及其随机性的研究[D].北京: 中国矿业大学北京研究生部, 1997.SHAN Ren-liang. Research on the mechnical model and random properties of rock failure under impact loading[D]. Beijing: Graduate School of China University of Mining and Technology, 1997.

[8]陈庆寿, 吴煌荣. 岩石在动载作用下的破坏与强度[J].武汉地质学院院报, 1987, 12(2): 208－216.CHEN Qing-shou, WU Huang-rong. Strength and fractures of rocks under dynamic loading[J]. Journal of Wuhan College of Geology, 1987, 12(2): 208－216.

[9]翟越, 马国伟, 赵均海, 等 .花岗岩和混凝土在单轴冲击压缩荷载下的动态性能比较[J]. 岩石力学工程学报,2007, 26(4): 762－768.ZHAI Yue, MA Guo-wei, ZHAO Jun-hai, et al.Comparison of dynamic capabilities of granite and concrete under uniaxial impact compressive loading[J].Chinese Journal of Rock Mechanics and Engineering,2007, 26(4): 762－768.

[10]夏昌敬, 谢和平, 鞠杨, 等. 冲击载荷下孔隙岩石能量耗散的实验研究[J]. 工程力学, 2006, 23(9): 1－5.XIA Chang-jing, XIE He-ping, JU Yang, et al.Experimental study of energy dissipation of porous rock under impact loading[J]. Engineering Mechanics, 2006,23(9): 1－5.

[11]谢和平, 彭瑞东, 鞠杨. 岩石变形破坏过程中的能量耗散分析[J]. 岩石力学与工程学报, 2004, 23(21): 3565－3570.XIE He-ping, PENG Rui-dong, JU Yang. Energy dissipation of rock deformation and fracture[J]. Chinese Journal of Rock Mechanics and Engineering, 2004,23(21): 3565－3570.

[12]ZHANG Q B, ZHAO J. Determination of mechanical properties and full-field strain measurements of rock material under dynamic loads[J]. International Journal of Rock Mechanics and Mining Sciences, 2013, 60: 423－439.

[13]巫绪涛, 孙善飞, 李和平. 用HJC本构模型模拟混凝土SHPB实验[J]. 爆炸与冲击, 2009, 29(2): 137－142.WU Xu-tao, SUN Shan-fei, LI He-ping. Numerical simulation of SHPB tests for concrete by using HJC model[J]. Explosion and Shock Waves, 2009, 29(2): 137－142.

[14]朱万成, 尚世明, 李占海, 等. 动态载荷作用下混凝土破裂的数值模拟[J]. 建筑材料学报, 2008, 11(6): 709－714.ZHU Wan-cheng, SHANG Shi-ming, LI Zhan-hai, et al.Numerical simulation on spalling of concrete under dynamic loading[J]. Journal of Building Materials,2008, 11(6): 709－714.

[15]孙善飞, 巫绪涛, 李和平, 等. SHPB实验中试样形状和尺寸效应的数值模拟[J]. 合肥工业大学学报(自然科学版), 2008, 31(9): 1509－1512.SUN Shan-fei, WU Xu-tao, LI He-ping, et al. Numerical simulation of effects of specimen size and shape in SHPB experiment[J]. Journal of Hefei University of Technology (Natural Science), 2008, 31(9): 1509－1512.

[16]张凤国, 李恩征. 混凝土撞击损伤模型参数的确定方法[J]. 弹道学报, 2001, 13(4): 12－16.ZHANG Feng-guo, LI En-zheng. Amethod to determine the parameters of the model for concrete impact and damage[J]. Journal of Ballistics, 2001, 13(4): 12－16.

[17]李夕兵, 古德生. 岩石冲击动力学[M]. 长沙: 中南工业大学出版社, 1994.LI Xi-bing, GU De-sheng. Rock impact dynamics[M].Changsha: Central South University of Technology Press,1994.