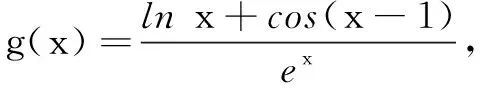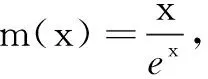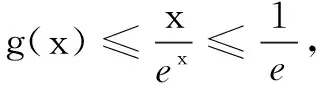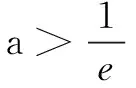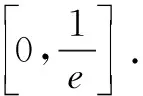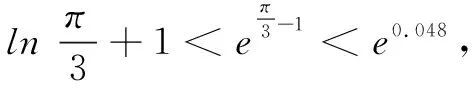一道“曲率”题的强烈辐射

王 勇 陈靖逸

(湖北省襄阳市第一中学，441000)

2021年1月23日是值得纪念的日子,由国家教育部命题考试中心统一命题,江苏、河北、辽宁、福建、湖北、湖南、广东和重庆等八省市高三学生参加的大联考拉开序幕,考生总人数达331万，约占全国高考总人数的三分之一,这也是中国历史上第一次大规模的联考,绝对可以载入史册.本次大联考数学试卷中的立体几何题的背景及考查点令人耳目一新,试题以大兴机场的建设成就和高等数学中的微分几何为背景,考查新定义“空间弯曲率”——“曲率”,对学生获取信息能力、抽象概括能力、理解能力要求较高,是大联考的一大亮点.下面给出此题的深刻剖析及此题的几道变式题,供同学们研读.

一、试题分析

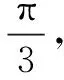
(1)求四棱锥的总曲率;

(2)如果多面体满足顶点数-棱数+面数=2,证明:这类多面体的总曲率是常数.

解(1)如图2,四棱锥共有5个顶点,5个面.

四棱锥所有面角之和等于4个三角形内角之和再加上1个四边形的内角之和.故四棱锥的总曲率=5×2π-4×π-2π=4π.

(2)解法1设多面体顶点数为V，棱数为E，面数为F，则V-E+F=2.

多面体的总曲率=V×2π-多面体所有面角之和=V×2π-多面体的所有面的内角之和.

多面体的面均为多边形,由多边形的内角和公式可知,在多面体的所有面的内角之和的计算过程中,每条棱都计算了两次,所以多面体的所有面的内角之和等于2E×π-F×2π,从而多面体的总曲率为V×2π-2E×π+F×2π=(V-E+F)×2π=4π.因此,这类多面体的总曲率是常数.

解法2设多面体顶点数为V，棱数为E，面数为F，则V-E+F=2.

设多面体的F个面分别是ni(i=1,2,…,F)边形，因为ni边形的内角和为(ni-2)π，且满足n1+n2+…+nF=2E(每条棱被两个面公用，算作两条边)，所以多面体的总曲率

K=V×2π-多面体所有面角之和

=V×2π-多面体的所有面的内角之和

=V×2π-(n1+n2+…+nF-2F)π

=V×2π-(2E-2F)π

=2π(V-E+F)=2π×2=4π.

因此,这类多面体的总曲率是常数.

评注(1)该题打破传统的出题模式,大胆创新的命题方式符合新高考的“多变性”,体现了时代特色.

(2)欧拉定理V-E+F=2(其中V为顶点数，E为棱数，F为面数)是简单多面体的一个几何不变性质,也是推出总曲率为常数的依据.以命题形式进行普及,加深了学生的认知.破解本题的关键是转化,一是整体上来看,所有顶点处的面角之和等于多面体每个表面的多边形的内角和;二是多面体的总曲率=2π×顶点数-所有表面多边形的内角之和.

(3)第(2)问的解法1是命题组给出的标准答案,比较抽象,学生理解有困难;而解法2的思路自然流畅,通俗易懂,值得借鉴.

二、强烈辐射

(A)a>b>c>d

(B)a>b>d>c

(C)b>a>d>c

(D)c>d>b>a

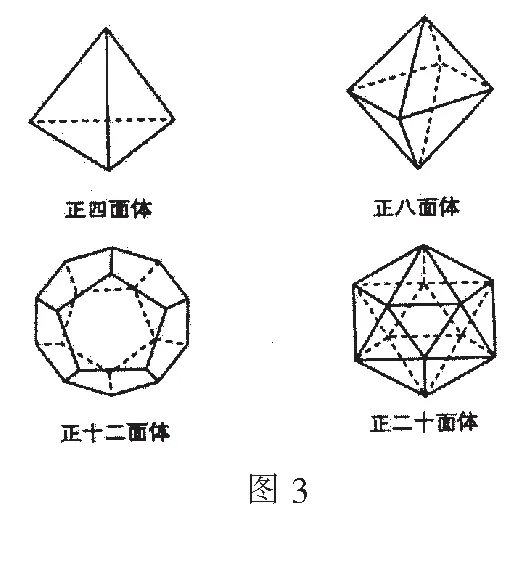
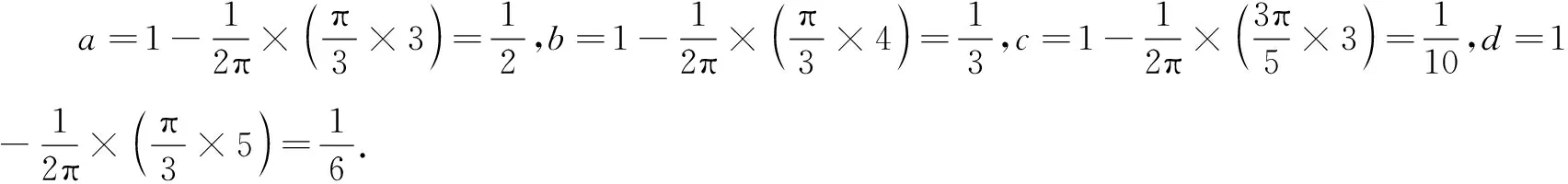
评注本题给出多面体M在点P处的离散曲率的计算公式及内涵解读,要求学生在阅读理解的基础上分别计算四类具体正多面体在各顶点处的离散曲率,再比较大小,有效考查了学生的空间想象能力、运算求解能力,对平面几何知识的考查也相当充分.

例3如图4,在正三棱锥S-ABC中,D,E,F,G分别为SA,SC,BC,AB的中点.

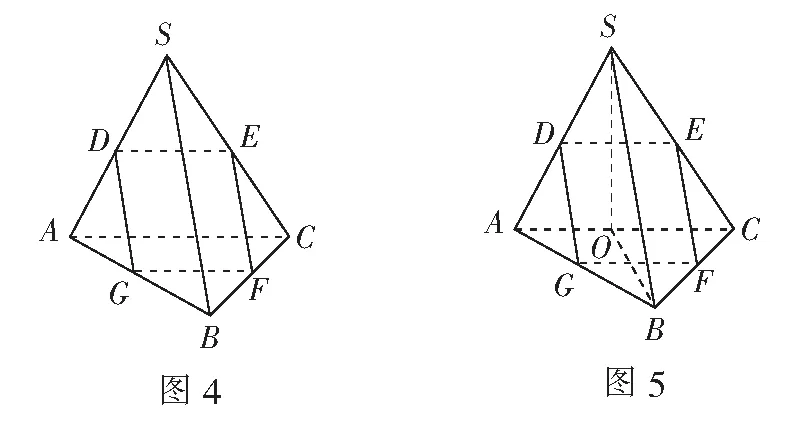
(1)证明:D,E,F,G四点共面,且AC∥平面平面DEFG；

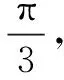
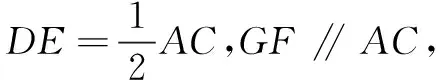
又AC⊄平面DEFG，DE⊂平面DEFG，所以AC∥平面DEFG.

(2)由(1)可得DE∥GF，且DE=GF，所以四边形DEFG为平行四边形.

于是,由AB=2，可知∆SAB,∆SBC,∆SAC都是斜边长2的等腰直角三角形,∆ABC为边长为2的正三角形.

如图5，取AC的中点O，连结SO，BO，则SO⊥AC，BO⊥AC.又SO∩BO=O,所以AC⊥平面OBS.

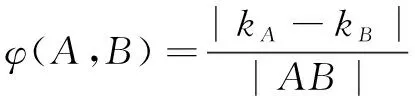
(A)存在这样的函数,该函数图象上任意两点之间的“曲率”为常数

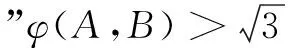
(C)函数f(x)=ax2+b(a>0,b∈R)图象上任意两点A,B之间的“曲率”φ(A,B)≤2a

(D)设A(x1,y1),B(x2,y2)是曲线f(x)=ex上不同两点,且x1-x2=1,若tφ(A,B)<1恒成立，则实数t的取值范围是(-∞,1).

分析本题是多选题,是新高考标志性的新题型.根据题设中引入曲线上两点间“曲率”的定义,可利用导数的几何意义并结合特例法、放缩法获解.

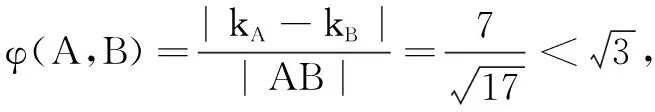
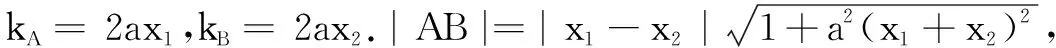
综上，选AC.

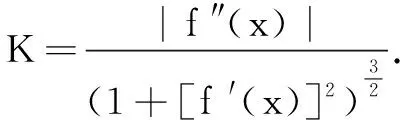
(1)求b的值；

(2)若函数f(x)存在零点，求a的取值范围；

(3)已知1.098

解(1)当a=0时，f(x)=-lnx-bcos(x-1),所以f(1)=-b.

(2)由(1)知f(1)=aex-lnx-cos(x-1).令f(x)=0,得

由此易见h(x)在(0,1)单调增，在(1,+∞)单调减.所以h(x)≤h(1)=0,即lnx+1≤x.

综上，1.14

评注本题以曲率为媒介,主要考查函数的求导运算、零点和放缩法,考查的学科素养是理性思维、数学应用和数学探索.