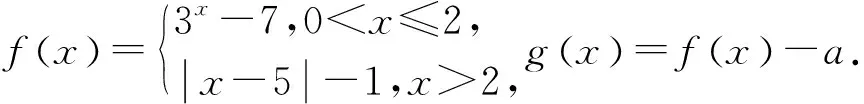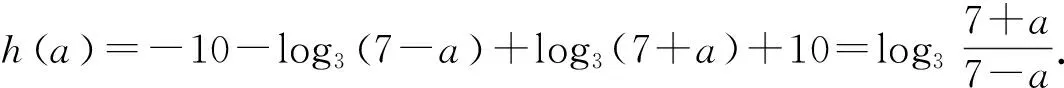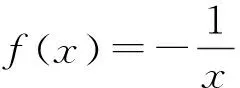借助函数模型 破解问题难点

安徽省合肥市第四中学 (233000) 管良梁

数学模型是数学基础知识与数学应用之间的桥梁，构建数学模型处理数学问题的过程，就是将数学理论知识应用于实际问题的过程.借助合适的数学模型，有助于破除解题时遇到的难点，使得数学问题得以解决.接下来笔者结合3个案列谈谈借助合适数学模型的重要性.

1 模型f(x)=x2

题1 已知函数f(x)=x2-2x+a(ex-1+e-x+1)有唯一零点，则a=( ).

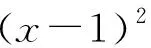
评注：因为解答过程中“因为函数f(x)有唯一零点，所以函数h(t)的图象与直线y=a有唯一交点，所以此交点的横坐标为0”理解起来不是特别容易，所以可以借助偶函数f(x)=x2.易知t=1时，函数g(x)=t和函数f(x)=x2只有1个交点，此时x=0.借助模型f(x)=x2对“易得h(t)为偶函数因为函数f(x)有唯一零点，所以函数h(t)的图象与直线y=a有唯一交点，所以此交点的横坐标为0”加以理解，使得本题解答过程中的难点得以破解.

2 模型f(x)=|lnx|

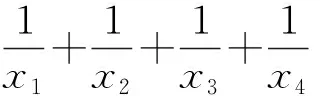
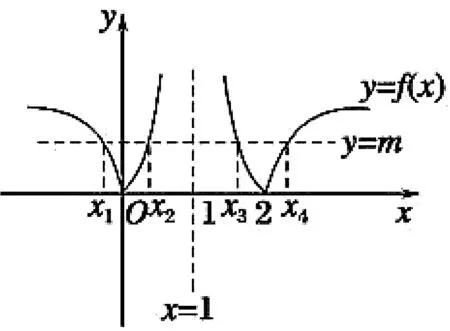
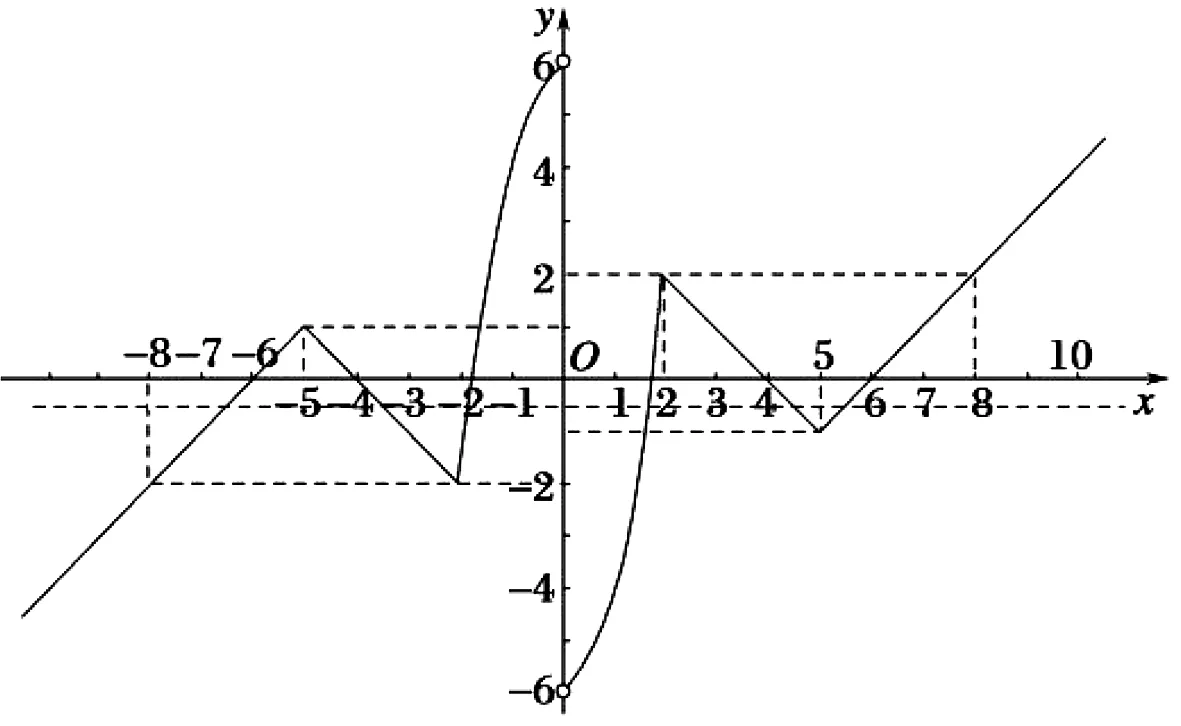
图1

解析：函数函数f(x)=|loga|x-1||(a>0且a≠1)的图象如图1所示.不妨设f(x1)=f(x2)=f(x3)=f(x3)=m(m>0)，由于f(x1)

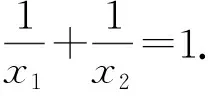
评注：解答过程中的“由|loga|x1-1||=|loga|x2-1||，得loga(1-x1)=-loga(1-x2)”不容易理解，很容易出错.借助函数f(x)=|lnx|，对其加以理解.当x1

3 模型

(1)若函数g(x)恰有三个不相同的零点，求实数a的值；(2)记h(a)为函数g(x)的所有零点之和.当-1

图2

数学问题比较综合、比较抽象，逻辑性也比较强,需要选择合适的方法处理所遇问题.当问题初次见面，不太熟悉，甚至很陌生时，怎么办？首先需要将所遇问题进行归类，然后选取此类问题的基础模型.通过对基础模型的认知，对所遇问题加以研究.这样就可以借助模型破解所遇问题的难点，使得问题得以解决.