混合式教学模式在线性代数教学中的应用

朱青

摘要：线性代数是一门重要的专业基础课程，在专业学习和实际生活中都有广泛的应用，为培养高素质应用型人才提供必备的基础知识。阐述混合式教学模式的内涵，明确线性代数课程体系，研究混合式教学模式在线性代数教学中的应用，并给出案例分析。通过开展混合式教学，培养学生的自主学习能力，提高学生的抽象思维能力以及解决实际问题的能力。

关键词：线性代数;混合式教学;信息技术;数学软件;在线教学平台

中图分类号：G642        文献标识码：A

文章编号：1009-3044（2022）06-0175-03

开放科学（资源服务）标识码（OSID）：

线性代数是理工农林类院校各专业的一门重要课程，在众多专业领域中应用广泛。传统教学模式下，以教师讲授为主，学生被动学习，学生的自主学习能力较差，没有得到相应的培养。另外，由于课程较为抽象难懂，并且教学过程普遍重理论轻应用，学生缺乏学习兴趣，学习积极性不高。随着信息技术的快速发展，基于“线上 + 线下”的混合式教学成为高等教育发展的一个新方向。混合式教学模式下，线性代数教学发生了重大变革，传统的教学方法、教学手段需要改变和调整，线性代数教学需要注入新的生机和活力。

1 混合式教学模式的内涵

混合式教学模式强调将传统的课堂教学与网络教学相结合，在教师的引领下，培养学生的自主学习能力，提高学生的学习兴趣和积极性，全面提升教学效果。经过广大教育工作者的努力探索，逐步摸索出一条适应我国高等教育发展的道路。目前，普遍认可“MOOC+翻转课堂”或“SPOC+翻转课堂”的形式，可将整个教学环节分成三部分。课前，将自主学习任务单、教学视频、讨论题、拓展阅读等相关资料上传至网络教学平台，学生通过观看视频进行自主学习;课中，在教师的引导和学生的积极参与下，开展翻转课堂;课后，师生之间通过网络开展交流互动、辅导等活动。

在这种新的教学模式下，由于课前学生已经进行自学，课中环节教师应充分发挥学生的主体地位，采用多种教学策略，有效开展翻转课堂。一方面，利用启发引导、重点答疑、小组讨论、学生展示等各种方式，充分发挥学生的主体地位;另一方面，在“黑板+多媒体”的传统教学手段上，结合学习通、雨课堂等智慧教学工具，提高学生的学习积极性和参与度。

2 线性代数课程体系

多年来，通过众多教育者的努力，我国线性代数课程的内容体系改进了许多，部分教材加入了实用性案例以及MATLAB实验指导。

1） 理论内容。线性代数研究向量、向量空间、线性变换和线性方程组，国内教材主要包括矩阵、行列式、线性方程组、向量空间、特征值与特征向量、二次型[1]。线性代数有着严谨的逻辑推理，知识内部关联性较强，重视论证与计算，具有高度的抽象性。

2） 应用案例。线性代数在自然科学众多领域中有重要的应用，并且进一步渗透到经济、管理等社会科学领域，很多专业领域均可利用线性代数知识来解决技术问题。例如：投入产出分析、动态经济模型、人口预测模型、交通流模型、微分动力系统、遗传模型、图像处理、复合材料开发、大规模集成电路设计、信号处理、线性规划、弹性钢梁受力形变等很多方面都有应用。对此，我们强调通过数学模型来解决各领域中的实际问题，建立应用案例进行研究并加以推广。

3） 课程实验。在线性代数中，以高阶线性方程组的求解为例，计算的复杂程度以及较大计算量都阻碍了线性代数在各领域中的应用和发展。对此，需要利用计算机和数学软件开展相应的数学实验，从而摆脱复杂的数值计算，促进数学应用方面的发展。最常用的MATLAB软件，可以进行多种运算，并且具有操作方便、数据可视化等一些特点，对于解决相关计算问题、提高解题效率非常有帮助。

3 混合式教学模式下线性代数教学策略

3.1 利用线上教学平台，开展课前预习任务

混合式教学模式下，课前教师通过线上教学平台发布学习资源，主要包括自主学习任务单、教学视频、思考题、讨论题等，以供学生课前预习。通过发布课前自学任务，可以为学生提供学习指导与帮助，学生带着任务自学，一定程度上可以克服学习惰性。通过学习任务的引领，学生可以初步了解所学内容的重难点、前后联系以及线性代数在不同领域的应用情况，学生的自主学习能力得到进一步的提升。

案例1 以“线性方程组与矩阵的初等变换”为例，课前布置自学任务：①给出一个三元线性方程组，让学生利用中学阶段所学的高斯消元法解方程组;②引导学生观察“方程的变换”与“增广矩阵的变换”之间的关系;③总结变换类型;④观察行阶梯形矩阵、行最简形矩阵的特点;⑤引导学生将增广矩阵化为行最简形矩阵，即可求出方程组的解;⑥通过学习，总结解线性方程组的步骤。通过考查学生对任务的完成情况，课堂中教师可以有侧重点组织教学活动。

3.2 开展合作学习模式，构建师生学习共同体

传统教学模式下，基本以教师讲授为主，学生学习过程相对孤立，师生之间、生生之间缺乏一定的交流与互动。混合式教学模式强调在教师的引领下，发挥学生的主动性和积极性，师生之间相互学习与交流。因此，可以将教学班级分成若干个小组，小组成员之间共同学习、研讨，通过这种方式进一步激发他们思想碰撞的火花。一般每四人为一小组，课前可以相互督促自学，课中可以进行小组讨论，课后可以开展学习互助。尤其对于一些较为复杂的问题或项目，通过开展小组内部以及小组之间的协同合作，不断修正并完善討论结果，学生的学习主动性得到了很大的提升。

案例2 以讨论“矩阵、行列式、方程组、向量组之间的内在联系”为例，通过课堂教学实践发现，不同小组从不同角度进行了汇报。虽然有些小组总结不太全面，但是在讨论的过程中，同学之间相互帮助，学习能力较强的学生带动其他学生，相互之间分析讲解，进一步加深了知识的理解。

下面给出其中一个小组的汇报结果进行展示，对于[n]阶方阵[A]，得出以下命题等价：①线性方程组[Ax=0]只有零解;②矩阵[A]的秩等于[n];③矩阵[A]的行（列）向量组的秩等于[n];④矩阵[A]的行（列）向量组线性无关;⑤矩阵[A]的行列式不等于0;⑥矩阵[A]可逆。通过小组讨论，最终建立了知识单元的关系链，学生对线性代数的知识结构有了更深的认识和理解。

3.3 利用智慧教学工具，活跃课堂气氛

线性代数具有抽象、严谨、计算量大等特点，很多过程需要进行论证、计算，多数教师采用“黑板+粉笔+PPT”的教学手段。但是传统的教学模式下，学生被动听讲，课堂气氛比较沉闷，部分学生感到枯燥、无趣，学生学习的积极性并不高。对此，可以利用智慧教学工具活跃课堂气氛，提高学生学习的积极性和参与度。常用的学习通、雨课堂等教学工具，均具有提问、抢答、讨论、弹幕、投票、统计等功能，在恰当的时机使用这些功能，可以缓解课堂的紧张气氛，使学习过程变得多样化。

案例3 以矩阵和行列式的运算为例，进行投票活动：以下正确的是？

A. [kA=kA]，其中[A]为方阵;

B. 矩阵运算满足[A+B=B+A];

C. 矩阵运算满足[AB=BA];

D. [A+B=A+B]，其中[A，B]为方阵;

E. [AB=AB]，其中[A，B]为方阵;

F. [AB=BA]，其中[A，B]为方阵。

正确答案为B、E、F，通过投票结果发现，出现问题较多的选项为A、F，其次为选项D、E，说明学生对于矩阵、行列式运算法则理解不够深入，需要老师详细分析或给出反例。通过投票环节的数据统计功能，使得教师能够全面了解全班同学对于某个知识点的掌握程度。

3.4 利用多媒体，加强交互性与可视化

线性代数和几何联系紧密，很多概念和知识都有一定的几何背景，目前国内线性代数教材，普遍缺乏相关的几何背景，使得学生学起来更加的抽象，对于线性代数的本质不甚了解。对此，教师在上课过程中可以利用多媒体，采用交互性、可视化的方式，展示相关的几何背景，加深学生对线性代数几何意义的理解，使得课程变得形象生动。

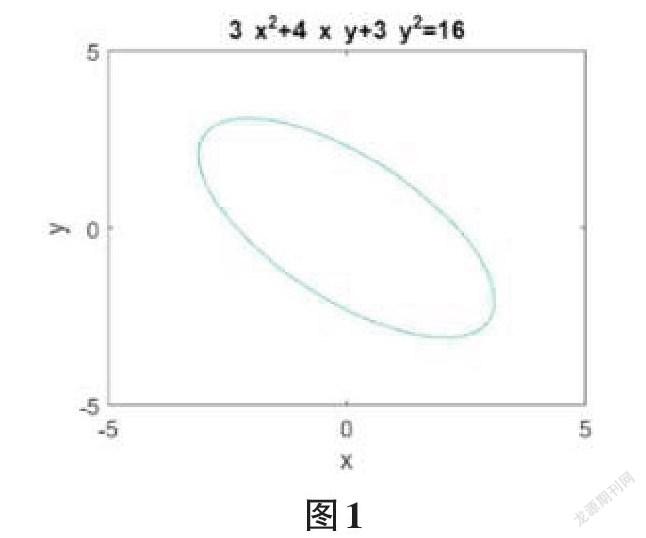
案例4 以“正交变换化二次型为标准形”为例，说明正交变换保持几何图形形状不变[2]。将二次曲线[3x2+4xy+3y2=16]（图1），化为标准方程[x2+5y2=16]（图2），通过观察可知，二次曲线为椭圆，变换前后形状不变。

通过作图，还可以解释二次型的正定（负定、不定）性。例如[fx，y=x2+5y2]为正定二次型（图3），[fx，y=-x2-5y2]为负定二次型（图4），[fx，y=x2-5y2]为不定二次型（图5）。

3.5 结合MATLAB软件，开展实用性案例研究

线性代数是一门重要的专业基础课程，在工程技术、计算机科学、社会科学、经济管理等领域中有重要应用，为培养高素质应用型人才提供必备的基础知识。传统的教学模式下，教师几乎把全部课堂时间用于讲授理论知识，学生明显感到枯燥、无趣且缺乏应用价值，这在一定程度上降低了学生的学习兴趣，学生的学习动力不足。对此，在混合式教学模式下开展翻转课堂，要把理论知识、对应不同专业需求的实用性案例、MATLAB实验指导这三部分内容有机结合在一起，以此丰富线下课堂教学，提升教学效果。

案例5 常见的线性变换类型有恒等变换、伸压变换、反射变换、旋转变换、投影变换、切变变换，给出线性变换在图像处理方面的应用[3]。以沿[x]轴的切变变换[Y=AX]为例，其中[A=1k01]，给出矩阵：

[X=001014.574.5708081071075.515.5110010]

为字符H图形的各个节点。利用MATLAB作图功能，当[k=0.25]时，图像发生了如下变化（图6）。

把理论与实际结合，让学生一开始就知道学习线性代数是有用的，将来可以解决生活中的一些实际问题，并为接下来的后继专业课学习打好基础。

4 結束语

混合式教学模式强调学生的主体地位，教师应结合不同专业学生的需求，制定相应的授课计划，注重知识的扩展和能力的提高。一方面，教师应充分发挥启发、引领作用，创设良好的课堂环境，提高学生的抽象思维能力以及解决实际问题的能力;另一方面，教师应充分利用信息技术，为学生提供更丰富的学习内容、更多样化的学习形式，提高学生的学习兴趣和积极性，提升教学效果。

参考文献：

[1] 同济大学数学系.线性代数[M].北京：人民邮电出版社，2017：1-2.

[2] 王杰.MATLAB可视化效果在线性代数教学中的应用[J].淮南师范学院学报，2010，12（3）：101-102.

[3] 陈怀琛.实用大众线性代数（MATLAB版）[M].西安：西安电子科技大学出版社，2014：93-94.

[4] 郑颖春.基于SPOC的“线性代数”课程教学模式的探索[J].牡丹江教育学院学报，2020（2）：75-77.

[5] 郭宏博.基于多媒体的线性代数教学案例分析[J].电子技术，2020，49（9）：46-48.

【通联编辑：王力】