晶体结构教学中两个易困惑处的研究与探讨

杨 军

(1. 中国科学院过程工程研究所，北京 100190；2. 中国科学院大学 材料与光电技术学院，北京 100049)

材料的晶体结构(晶体中质点在三维空间的具体排列方式)是“材料科学基础”课程的重要内容[1-8]. 不同的固体材料具有不同的晶体结构，材料的性能也通常都与其晶体结构有关，因此研究和调控材料的晶体结构，对材料的研发、制造和使用均具有重要的意义. 晶体结构章节的内容不仅是材料科学课程的要求，也是深入学习其它许多专业课程如“固体物理”“材料分析表征”和“材料加工技术”等不可或缺的基础.

人们假定理想晶体中的实际质点都是固定不动的钢球，则可认为晶体是由这些钢球遵循一定几何规律堆积而成. 为研究方便，忽略构成晶体的实际质点的体积，将其抽象成为纯粹的几何点，并将质点排列的周期性抽象成只有数学意义的周期性的图形，称为空间点阵. 早在1848年，法国物理学家奥古斯塔·布拉菲就已确定空间点阵只有14种形式，分成7个晶系，分别是三斜、单斜、正交、四方、立方、六方和菱方. 在通常使用的《材料科学基础》教材中，限于课时和内容，不会从数学角度严格的论证空间点阵的14种形式，而是向7个晶系晶胞的底心、体心和面心添加等同点，得到28种点阵形式，再通过点阵变换的方式论证只有14种形式. 这种方式简单直接，易于理解和接受，但大多数教材都没有讨论变换适用的范围或者边界，教学实践和学生的理解程度之间经常会产生矛盾.

另外，针对六方晶系，人们通常使用四轴指数代替三轴指数对晶面进行标记，这样晶系中的等价晶面具有相似的指数，很容易进行识别.但根据几何知识可知，三维空间独立的坐标轴最多不超过3个.对六方晶系来讲，确定了晶面在a1和a2轴上的截距，它在a3轴上的截距也就随之而确定.因此四指数表示在a1、a2和a3轴上截距倒数的h、k和i3个指数之间并不是相互独立的关系，其中只有两个是独立的，它们之间存在一个等量关系，即i=-(h+k).但可能是限于课时的缘故，当前的教材在这个地方都是一笔带过[9-13]，有的甚至认为这是一个人为附加的条件，有的教材中把这个等量关系联系到a1、a2和a3轴的矢量关系，认为可由a3=-(a1+a2)导出，但也没有给出详细说明[14].笔者在教学过程中发现，学生很容易在这个地方产生困惑，面对很多刨根问底的学生，不得不在课堂上花大量时间讲解这个知识点，授课进度反而受到影响.因此，本文就这个知识点给出了三种证明方法，涉及从繁琐的余弦定理到简洁的初等几何和矢量方法，供有兴趣的学生自己阅读，也弥补当前一些教材的不足之处.

1 关于点阵变换讨论点阵类型

我们已经知道，空间点阵可以划分为7个晶系.那么，这7个晶系中包含多少种空间点阵呢？这就取决于每种晶系可以包含多少种点阵，或者说有多少种可能的阵点分布方式.法国物理学家奥古斯塔·布拉菲已经于1848年用严格的数学方法证明了空间点阵只能有14种.但区别于数学方法，不妨这样考虑：空间点阵的阵点必须是等同点，而由于晶胞的8个角隅、6个外表面的中心(面心)以及晶胞的中心(体心)都是等同点，故乍看起来应如图1所描述的那样，每种晶系都包括4种点阵，即简单点阵(P)、体心点阵(I)、底心点阵(C)和面心点阵(F).这样7个晶系总的点阵类型应该是28种.然而，只要将这些点阵逐一画出，通过简单的变换就会发现，其中有些点阵是完全相同或等价的，真正不同的点阵如布拉菲已经证明的那样，只有14种，包括简单三斜、简单单斜、底心单斜、简单六方、简单正交、体心正交、底心正交、面心正交、简单菱方、简单四方、体心四方、简单立方、面心立方和体心立方点阵.下面先看一些成功的例子.

图1 从阵点为等同点角度理解每个晶系应包含的点阵类型

例1：用点阵变换的方式解释为什么底心三斜布拉菲点阵不是一个新点阵.如图2所示，底心三斜布拉菲点阵可以变换成体积更小的简单三斜布拉菲点阵，故它不是一个新点阵.这涉及晶胞的选择标准，选取的晶胞在满足反映点阵对称性的前提下，应具有最小的体积.

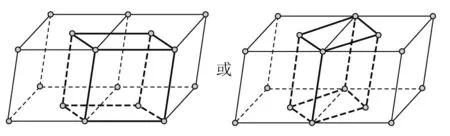
图2 底心三斜布拉菲点阵可以连成简单三斜布拉菲点阵

例2：用点阵变换的方式解释为什么底心四方和面心四方布拉菲点阵不是新点阵.这个变换可以用图3表示，底心四方点阵可以连成体积更小的简单四方点阵(图3右图)，而面心四方点阵则可以连成体积更小的体心四方点阵(图3左图)，故它们都不是新的布拉菲点阵.

图3 底心四方和面心四方布拉菲点阵可以分别连成简单和体心四方布拉菲点阵

例3：用点阵变换的方式解释一下为什么体心单斜和面心单斜布拉菲点阵不是新点阵.由图4可以看出，2个体心单斜和2个面心单斜都可以连成一个底心单斜点阵，因而不是新的点阵.单斜布拉菲点阵中，体心和底心点阵虽然可以互相转换，但据群论分析的结果，底心单斜是正确的布拉菲点阵选择，能够体现对称元素在晶胞中的相应方位.

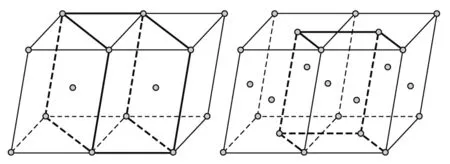
图4 体心单斜和面心单斜布拉菲点阵都可以连成底心单斜布拉菲点阵

上面的几个例子说明一些点阵可以通过简单变换连成体积更小的简单点阵或其它更能体现晶体对称元素的等价点阵，因而不是新点阵.但学生易于困惑的问题随即涌现出来，即底心点阵似乎都可以连成体积更小的简单点阵(参考例1和例2)，那为什么还会有底心单斜和底心正交点阵呢？针对这个困惑可以看看变换后的结果.

如图5(a)和图5(b)所示，底心单斜点阵经过类似例1或例2的变换处理后，变成了简单三斜点阵，而底心正交点阵经过类似变换处理后则变成了简单单斜点阵(同学们可根据教科书上的晶系参数特征自行确证)，已经和原来的点阵不属于同一个晶系.事实上，所有14种空间点阵都可以用简单点阵来描述，如图5(c)和图5(d)所示的体心立方和面心立方点阵.分别可以用简单单斜和简单菱方点阵来表示，这种表示方法实际是在寻找非初级晶胞(含两个或两个以上阵点的晶胞)的原胞(只含一个阵点的晶胞)，但如此获得的简单点阵和原来的点阵不属于同一个晶系，它们具有不同的对称元素，当然不能从这些变换否定体心立方和面心立方点阵的存在，实际上它们确实存在，而且在金属晶体中非常常见.因此需要明确指出，通过点阵变换来说明某个点阵不是新的布拉菲点阵需要在同一晶系内进行，变换后成为另一晶系的点阵则不能否定该点阵的存在.例如，在有的教科书中，通过将底心六方(向垂直于c棱边的面添加阵点)、体心六方和面心六方点阵变换成简单正交、面心正交和体心正交点阵的方式，说明这些点阵不是新点阵(变换的方式如图6所示)，这是不正确的，而是添加这些阵点后构成的点阵违背了六方晶系所特有的旋转对称特性.再如底心立方点阵，当然可以通过例1或例2的变换方式说明它不是一个新点阵，但从晶系的特征上看，立方晶胞的6个面是等价面，具有完全相同的性质，而底心立方点阵则违背了这一性质，故不存在底心立方点阵.

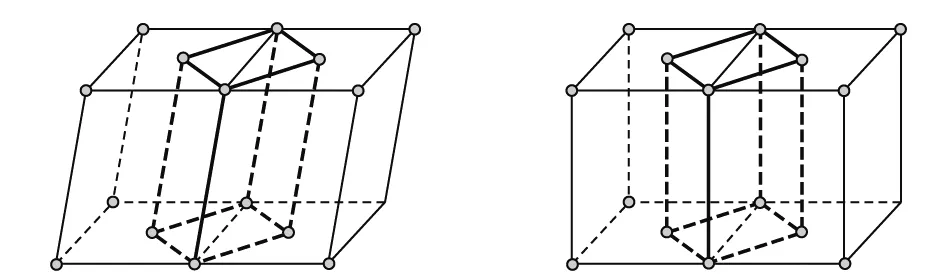
底心单斜点阵可以连成简单三斜点阵 底心正交点阵可以连成简单单斜点阵

底心六方

2 关于四轴指数的附加条件

四指数表示是基于4个坐标轴：a1、a2、a3和c轴，其中，a1、a2和c轴就是六方晶体原胞的a、b和c轴，如图7所示.六方晶系晶面四指数标注原理和方法同其它晶系中晶面三指数标注过程一样，步骤如下：① 先找出待标注晶面在4个坐标轴上的截距长度(以晶胞的点阵常数a、c为单位长度)；② 求其倒数并化为互质的最小整数，即得到四指数表示，标记为(hkil).从图7所示的几何关系，确定了待标注晶面在a1和a2轴上的截距，它在a3轴上的截距也就随之而确定.由此而知四指数表示中，h、k和i三个指数并不相互独立，其中只有两个是独立的.根据几何关系或向量分析，可确定它们之间存在一个等量关系，即i=-(h+k)，下面给出几个证明方法.

图7 六方晶体的四轴坐标系统

证法1 (余弦定理法)：如图8所示，暂不考虑正负号，实际是要证明OP长度的倒数等于OM长度和ON长度的倒数和，即要证明1/p=1/m+1/n.

图8 余弦定理法证明四指数表示中h、k和i三个指数等量关系示意图

基于余弦定理，有

(1)

(2)

2mncos 120°=m2+n2+mn

(3)

将l1和l2代入式(3)，可得

m2+p2-mp+n2+p2-np+

(4)

化简式(4)并移项处理，可得

mn+mp+np-2p2

(5)

将上式两边取平方，可得

4(m2+n2-mp)(n2+p2-np)=

(mn+mp+np-2p2)2

(6)

将式(6)展开并合并同类项，可得

3m2n2+3m2p2-6m2np+3n2p2-6mn2p+6mnp2=0

(7)

即

m2n2+m2p2+n2p2-2m2np-2mn2p+2mnp2=0

(8)

也即

(-mn+mp+np)2=0

(9)

故mn=mp+np，两边同除以mnp，最终得

(10)

再考虑到图8中坐标轴的方向，p实际取负值，故可得1/p=-(1/m+1/n)，根据晶面指数的定义即可得证i=-(h+k).

证法2 (初等几何法)：如图9所示，过N点作平行于OP的直线，交a1轴与A点；过M点作平行于OP的直线，交a2轴于B点，则根据相似三角形特性可得到

图9 初等几何法证明四指数表示中h、k和i三个指数等量关系示意图

(11)

所以有

(12)

图10 向量法证明四指数表示中h、k和i三个指数等量关系示意图

(13)

(14)

需要注意的是，当用4个指数如[uvtw]来表示六方晶系的某一空间一个矢量时，一样需要添加一个约束条件.类似于晶面指数的约束条件，四指数表示空间晶向时的约束条件是t=-(u+v)，但需要说明，这个约束条件是人为添加的，不像晶面指数中的约束条件具有严格的数学基础，这是因为晶向指数表示中的数是由晶向在平面3个轴上的截距整理而来，没有取倒数，虽然3个数不全都独立，但却不是数学上的等量关系.

3 结束语

利用点阵变换可简洁有效地判断一个点阵是否为新的布拉菲点阵，但需要明确，这些变换需要在同一晶系内进行，对称性不能改变，变换后成为另一晶系的点阵不能说明初始点阵不是一个新点阵；针对四轴指数标记晶面时的附件条件，本文给出了3种证明方法，表明这一附加条件具有严格的数学基础，有助于学生对这一知识点的理解，适合在教学实践中采用.