有关金属晶体结构中几个难点问题的归纳与分析
■
金属晶体作为物质结构模块的重点,虽然仍有许多未解之谜,但仅就高中化学而言,许多知识、理论已经基本成形,本文拟结合高考试题的考查热点加以总结归纳,以飨读者。
一、晶体结构的堆积模型
我们在分析金属晶体的内部结构时,通常从密堆积模型开始,晶体微粒可看成等径实心小球排列。因此,晶体微粒结构从一维、二维、三维逐次展开有以下几种。
1.一维只有一种密排列方式;二维有两种排列方式,一种是非密置层排列,另一种是密置层排列,如图1所示。
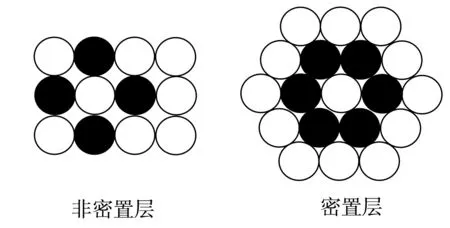
图1
2.三维空间的密置层与密置层排列有两种方式,如图2所示。
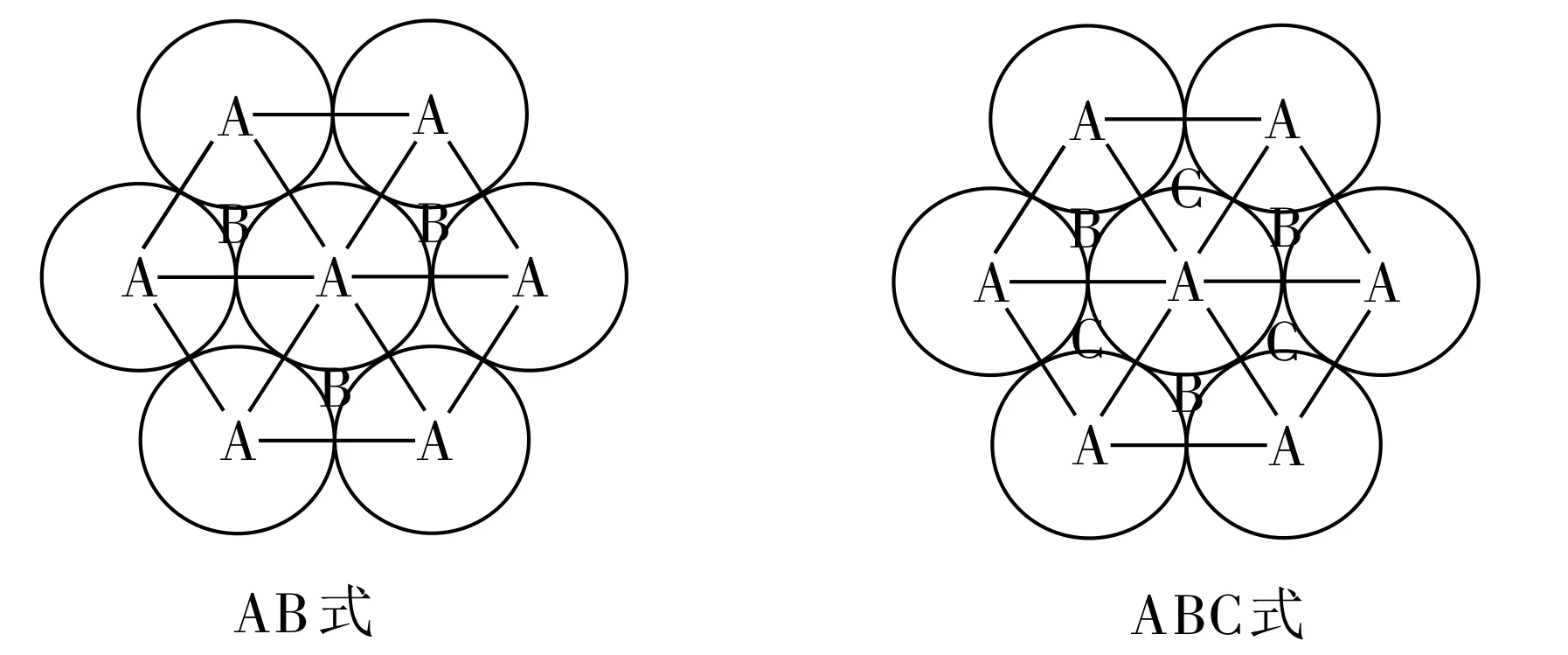
图2
(1)AB排列方式:第2层(即B层)对准第1层(即 A层)的1、3、5空隙或2、4、6空隙,第3层(即A层)对准第1层(即A层)的1、3、5空隙或2、4、6空隙,形成AB的简单重复。
(2)ABC排列方式:第2层(即B层)对准第1层(即A层)的1、3、5空隙,第3层(即C层)对准第1层(即 A层)的2、4、6空隙,第4层为A层的重复,形成ABC的简单重复。
二、晶胞的截取与晶胞微粒个数的均摊
1.晶胞的截取。晶胞都是从晶体结构中截取的六面体。根据重复、周期排列规则,截取的晶胞大小、形状完全相同且包含必要的循环元素。
2.晶胞微粒个数的均摊。
(1)简单立方堆积。由于1个晶胞上、下、左、右、前后并置构成整个晶体,因此,处于顶点的微粒实际属于8个晶胞共用,故此,此类晶胞实际“均摊”1个微粒。
(2)体心立方堆积。同理,在简单立方堆积的基础上,由于体心占有1个微粒,故本类晶胞实际“均摊”2个微粒。
三、晶体结构的若干计算
1.晶胞的参数(基本要素)。晶胞包含微粒个数及空间位置(空间坐标参数)两个参数。通常而言,晶胞的边长设为a,单位为pm(1pm=10-10cm)。
2.晶体的计算。
(1)空间利用率的计算。晶胞中实际占有的金属原子的总体积在整个晶胞空间中所占有的体积百分比即为空间利用率。计算思路:先确定晶胞微粒的个数,以圆的体积代替单个微粒的体积,求出微粒的总体积;再根据晶胞参数求出晶胞的体积;最后代入公式空间利用率计算即可。
晶胞参数与微粒半径的换算关系如下(以体心立方、面心立方为例,设边长为a,微粒半径为r):面对角线长体对角线长,体心立方堆积有面心立方堆积有
(2)晶胞密度的计算。先根据均摊法,求出每个晶胞实际包含的金属原子的个数,确定化学式,求出晶胞的总质量;再根据晶胞参数计算晶胞体积;最后根据进行计算求得结果。

