你若探究 花自盛开
——对一道高考解析几何题的探究
■
在解完2018年全国Ⅰ卷理科数学第19题后,笔者得到了椭圆中的等角性质,并将其性质拓展推广到其他的圆锥曲线中,在追溯其命题背景之后,又发现了圆锥曲线中等角性质的更一般形式,现分析如下。
一、试题呈现
题目(2018年全国Ⅰ卷理科数学第19题)设椭圆的右焦点为F,过F的直线l与C交于A,B两点,点M的坐标为 2,0( )。
(1)当l与x轴垂直时,求直线AM的方程;
(2)设O为坐标原点,证明:∠OMA=∠OMB。
评注:本题考查椭圆的标准方程及其几何性质、直线的方程、直线与椭圆的位置关系、斜率、韦达定理、等角的证明等基础知识,考查学生的推理论证能力、运算求解能力,以及综合运用所学知识分析问题和解决问题的能力,考查数形结合思想、分类讨论思想、化归与转化思想。立意深刻、内涵丰富,具有一定的典型性,极具探究价值。
二、试题解答

图1
三、拓展推广
1.在椭圆中的一般化推广
从上面的证法可知,对于一般的椭圆,只要M点为椭圆的右准线与x轴的交点,那么上述性质一定成立,即:
定理1:已知椭圆0)的右焦点为F,过F的直线l与椭圆C交于A,B两点,则 有 ∠AMF=∠BMF。(证法同上面的证法一样)
在上述定理中,我们发现焦点F与定点M的横坐标之间存在一定的联系,即乘积等于定值a2,那么,若将F点换成一般的点P(m,0),保证P,M两点的横坐标的乘积为定值a2,是否又有类似的性质呢?笔者借助GeoGebra软件进行探究,得出如下结论:
定理2:已知椭圆0),P(m,0)(-a<m<a且m≠0)是椭圆C内一点,过P点的直线l与椭圆C交于A,B
证明:当设直线AB与x轴重合时,结论显然成立。
当设直线AB与x轴不重合时,设直线AB的方程为x=ty+m,A(x1,y1),B(x2,y2),将x=ty+m代入椭圆C的方程得(t2b2+a2)y2+2tmb2y+(m2-a2)b2=0,则,故,则有∠AMP=∠BMP。两点
从而得直线AM与直线BM的倾斜角互补,所以∠AMP=∠BMP。
定理3:已知椭圆0),P(m,0)(m>a或m<-a)是椭圆C外一点,过P点的直线l与椭圆C交于A,B两点,则 有 ∠AMP=180°-∠BMP。(证明过程同定理2)
在定理3中,将直线l绕着P点旋转,当A,B重合时,∠AMP=∠BMP=90°,此时AM⊥x轴,直线l与椭圆C相切,于是我们进一步得出结论:
推论1:已知椭圆P(m,0)(m>a或m<-a)是椭圆外一点,过点作x轴的垂线,交椭圆C于A,B两点,则直线PA,PB与椭圆C相切。(如图2)
2.在双曲线、抛物线中的推广
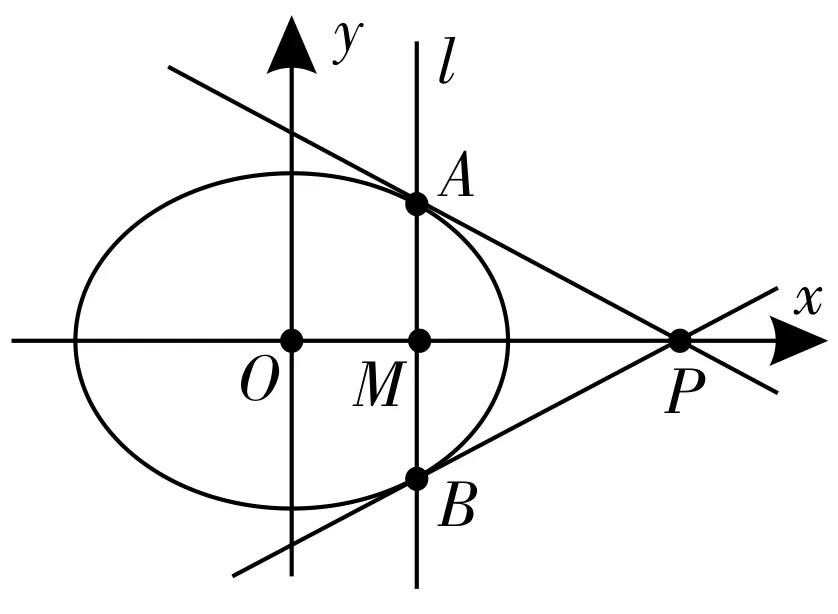
图2
类比椭圆,在双曲线、抛物线中是否有类似的结论呢?笔者又借助于GeoGebra软件进行了探究,得出以下结论:
定理4:已知双曲线0,b>0),P(m,0)(m>a或m<-a)是双曲线C内一点,过P点的直线l与双曲线C交于A,B两点,若A,B位于双曲线的同一支,则有∠AMP=∠BMP;若A,B位于双曲线的不同支,则有∠AMP=180°-∠BMP。
定理5:已知双曲线0,b>0),P(m,0)(-a<m<a)是双曲线C外一点,过P点的直线l与双曲线C交于A,B两点若A,B位于双曲线的同一支,则有∠AMP=180°-∠BMP;若A,B位于双曲线的不同支,则有∠AMP=∠BMP。(定理4、定理5的证明与定理2的证明过程类似,此处从略)
推论2:已知双曲线0,b>0),P(m,0)(-a<m<a)是双曲线C外一点,过点且与x轴垂直的直l线与双曲线C交于A,B两点,则直线PA,PB与双曲线C相切。
定理6:已知抛物线C:y2=2px,P(m,0)(m>0)是抛物线C内一点,过点P作直线l与抛物线C交于A,B两点,M(-m,0),则∠AMP=∠BMP。
证明:设直线AB:x=ty+m,A(x1,y1),B(x2,y2),将x=ty+m代入抛物线C的方程得y2-2pty-2pm=0,则y1+y2=2pt,y1y2=-2pm,所以从而直线MA,MB的倾斜角互补,所以∠AMP=∠BMP。
定理7:已知抛物线C:y2=2px,P(m,0)(m<0)是抛物线C外一点,过点P作直线l与抛物线C交于A,B两点,M(-m,0),则∠AMP=180°-∠BMP。
推论3:已知抛物线C:y2=2px,P(m,0)(m<0)是抛物线C外一点,过点M(-m,0)与x轴垂直的直线l与抛物线C于A,B两点,则直线PA,PB与抛物线C相切。

