空间平行关系之间转化框图的解读
■
人教版普通高中课程标准实验教科书《数学》必修2第二章章末小结中有空间平行关系之间的转化框图,如图1所示。
在复习中大家对此框图往往忽视、轻视或者无视,事实上,此框图是对空间平行关系内容的高度概括,方法的深度梳理,技巧的极度浓缩,值得多维度解读,对处理空间平行问题会大有裨益。
1.三种平行关系是一个知识整体
三个框表明空间平行关系有且只有三种,三种平行“情同手足”,密不可分。解决平行问题时思维应形成这样一种条件反射,即提到任一平行要自然想到另外两种平行,孤立地看待任一平行关系都无法顺利解题。
2.三种平行关系之间是互相转化的
三种平行关系这个整体是动态的,框图中的箭头表示不同平行关系之间是互相转化的。转化化归是解决平行问题最根本的思想方法,平行的判定是在不断地转化和更新中完成的,任意两种平行关系之间都是可以互化的,用图2表示三者之间的转化关系也许更恰当,转化的主要依据就是每种平行关系的判定定理和性质定理。每两种平行关系之间转化都是双向的,比如线面平行的判定理是由线线平行判定线面平行,反过来,线面平行的性质定理又可以由线面平行判定线线平行。
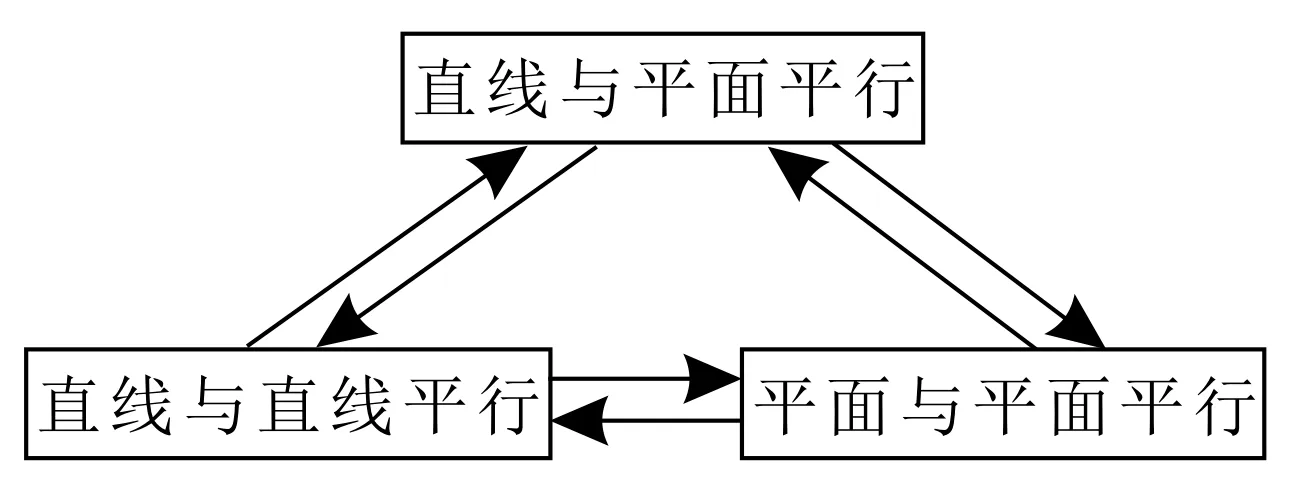
图2
例1如图3,在四面体ABCD中,截面PQMN是正方形,则在下列命题中错误的是( )。
A.AC⊥BD
B.AC∥截面PQMN
C.AC=BD
D.异面直线PM与BD所成的角为45°
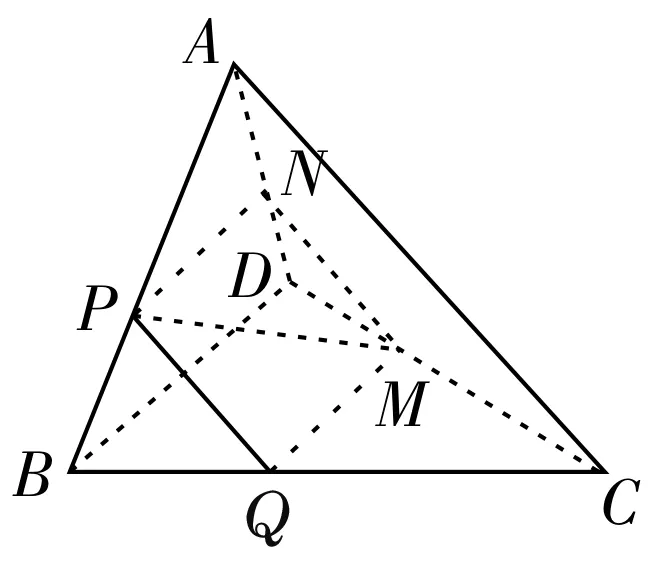
图3
解:因为截面PQMN是正方形,所以PQ∥MN。又PQ⊄面ADC,MN⊂面ADC,所以PQ∥面ADC。又因为面ABC∩面ADC=AC,PQ⊂面ABC,所以PQ∥AC。同理QM∥BD。故选项A,B,D正确,C错误。
3.线线平行是空间平行关系的基础
框图中的第一个框表明平行问题的突破口是线线平行,说明立体几何的源头在平面几何,这正是学习的盲点,离开线线平行,线面平行和面面平行就缺少了源头活水,无论怎么复习,都无法冲破平行判定的迷雾。因此同学们在学习时对线线平行的判定方法有必要进行如下补充:(1)平行线的定义;(2)三角形中位线平行底边;(3)梯形中位线平行上下底;(4)平行四边形(包括矩形、菱形、正方形)对边平行;(5)平行线的三个判定定理;(6)平行线分线段成比例定理逆定理;(7)同一平面内,垂直于同一直线的两条直线平行;(8)公理4(平行线的传递性)(9)线面平行的性质定理;(10)面面平行的性质定理;(11)线面垂直的性质定理;(12)两直线的方向向量共线。
4.线面平行是三种平行关系的核心
框图中的中间框就表明了线面平行的核心位置,线面平行上通面面平行下达线线平行,显示出线面平行判定的两种途径,既可以通过线线平行判定也可以通过面面平行判定。
例2如图4,平面PAC⊥平面ABC,E、F、O分别为线段PA、PB、AC的中点,G是线段CO的中点。证明:FG∥平面BOE。
证明:连接AF交BE于点Q,再连接OQ,因为E、F分别为线段PA、PB的中点,所以点Q是△PAB的重心,又O为线段AC的中点,G是线段CO的中点,所以2,所以FG∥OQ。因为FG⊄面BOE,OQ⊄面BOE,故FG∥平面BOE。

图4
线面平行的判定除了上面的方法,还有以下判定方法:(1)线面平行的定义;(2)若平面外的两条平行直线中的一条平行于平面,则另一条也平行于平面;(3)若一条直线平行于两个平行平面中的一个,则也平行于另一个;(4)垂直于同一直线的直线和平面平行(线应在平面外);(5)若直线的方向向量与平面的法向量垂直,则直线与平面平行(线应在平面外)。
5.面面平行也是空间平行关系的组成部分
框图中最后一个框表示的面面平行也是平行关系这个整体中必不可少的组成部分,它与另两种平行有着千丝万缕的联系,其判定方法分别如下:(1)面面平行的定义;(2)面面平行的判定定理;(3)面面平行判定定理的推论;(4)平行于同一平面的两个平面平行(平行面的传递性);(5)垂直于同一直线的两个平面平行;(6)若两个平面所夹的平行线段相等,则两平面平行;(7)法向量共线的两平面平行。
例3若a,b是异面直线,α,β是不同平面,a⊂α,b⊂β,a∥β,b∥α,则α∥β。
证明:在a上任取一点A,因为a,b异面,所以A∉b,记A,b确定的平面为γ,γ∩α=c。因为b∥α,b⊂γ,所以b∥c。因为b⊂β,c⊄β,所以c∥β。又a∥β,且a⊂α,c⊂α,a∩c=A,所以α∥β。
以上是笔者对框图的粗浅认识,读者可以接着探讨各平行关系的性质,以及各结论的图形表示和符号表示,并参考此文对教材中空间垂直关系之间的转化框图进行类比解读。

