均匀磁化永磁棒的磁场

陈伊涵，张译文，张艳芳，黄 飞

(1. 中国科学院大学 本科部，北京 100049；2. 中国科学院高能物理研究所，北京 100049；3. 中国科学院大学 物理科学学院，北京 101408；4. 中国科学院大学 核科学与技术学院，北京 101408)

赵凯华教授和陈熙谋教授主编的《电磁学(第4版)》[1]中有这样一道习题(第6章习题6.1-3)：“题图所示是一根沿轴向均匀磁化的细长永磁棒，磁化强度为M，求图中标出各点的B和H.”

图1 6.1-3题图

这里因为永磁棒“细长”且磁化强度沿轴向，对点1、2、3来说，可以将永磁棒看成无限长的，对点5、6来说，可以将永磁棒看成半无限长的，由无限长通电螺线管的磁场可知

B2=B3=0，

再由磁感应强度法向连续这一边界条件知

各点的磁场强度可由H=B/μ0-M计算得到

H1=H2=H3=0，

问题是，如果磁棒不是“细长”的，其轴线上各点的磁场分布如何？如果磁棒不是轴向均匀磁化的，而是横向均匀磁化的(如图2所示)，各点的磁场分布会怎样？进一步，如果磁棒是沿任意方向均匀磁化的，其轴线上的磁场又将如何？如果磁棒是无限长的，在轴向、横向及其它任意方向均匀磁化的情况下，其全空间的磁场分布又将如何？本文对这些问题逐一给出解答.具体地，我们综合运用分子电流观点和磁荷观点，系统地计算了沿轴向、横向及其它任意方向均匀磁化的有限长永磁棒在轴线上的磁场以及无限长永磁棒在全空间的磁场.据我们所知，对沿横向均匀磁化及沿其它任意方向均匀磁化永磁棒的磁场分布这一问题，本文属首次提及并给出详细解答.

图2 横向均匀磁化永磁棒磁场的示意图

需要指出的是，本文在永磁棒的不同磁化状态下，灵活采用了分子电流观点和磁荷观点来计算其磁场分布，但所得结果与采用哪种观点无关.正如赵凯华教授和陈熙谋教授在《电磁学(第4版)》[1]的6.2章节中详细论述的，虽然分子电流观点和磁荷观点所假设的微观模型不同，分子电流观点更符合物质的微观结构图像，磁荷观点不太符合磁介质的微观本质，但在这两种观点下得到的磁感应强度B和磁场强度H的宏观规律的表达式完全相同，因而用两种观点计算所得的具体结果也完全一样.从这个意义上说，这两种观点是等效的.在处理实际问题时，不同场合下灵活运用磁荷观点和分子电流观点，可以大大简化计算[2,3]，而所得结果是客观的，不依赖于采用哪种观点.

1 有限长永磁棒轴线上的磁场分布

1.1 轴向均匀磁化

永磁棒沿轴向均匀磁化，磁化强度矢量为M，磁化电流分布在永磁棒表面，其面密度为

i′=M×en

(1)

磁化电流等效为如图3所示的通电螺线管，永磁棒的磁感应强度完全由磁化电流产生.设水平向右为正方向，图中P点(P点可位于永磁棒内外轴线上)处的磁感应强度的大小为

图3 磁化电流形成的通电螺线管

将式(1)代入，并考虑方向，得永磁棒轴线上的磁感应强度为

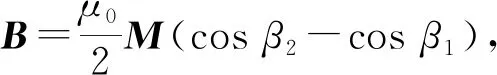
(2)

永磁棒轴线上的磁场强度可由H=B/μ0-M计算得到

(3)

1.2 横向均匀磁化

设圆柱型永磁棒长度为2L，半径为R，选圆柱体中点为坐标原点，磁化强度矢量M沿x轴正方向.我们用磁荷观点来分析该永磁棒轴线上的磁场.永磁棒内的磁极化强度矢量为

J=μ0M=μ0Mex

(4)

永磁棒内磁荷体密度为0，磁荷只分布在圆柱体表面，其面密度为

σm=J·en=Jcosθ

(5)

其中θ为永磁棒表面一点的法向方向与永磁棒磁化强度矢量之间的夹角，即永磁棒表面上一点在xy平面内与x轴的夹角，如图4所示.式(5)表明，永磁棒表面的磁化电荷面密度σm在z轴方向上是均匀分布的.

图4 永磁棒表面的磁荷分布图

如图5所示，将永磁棒切分为许多个高度为dl的薄圆盘，并继续将薄圆盘切分为许多个顶角角度为dθ的三棱柱，其磁化电荷量为

图5 微分法示意图

dqm=σmRdθdl=JRcosθdθdl

该三棱柱在轴上距离圆盘l处Q点产生的磁场强度沿x、y、z轴方向的分量分别为：

设轴线上Q点的坐标为(0,0,z)，积分得

进一步考虑式(4)，得

(6)

即永磁棒轴线上的磁场强度方向与永磁棒的磁化强度矢量方向相反.

永磁棒轴线上的磁感应强度可由B=μ0H+J计算得到

(7)

由式(7)知，在永磁棒外部，轴线上的磁感应强度方向相反.在永磁棒内部，轴线上磁感应强度方向与磁化强度方向相同，在永磁棒外则相反.

1.3 一般情况

我们已经得到了轴向均匀磁化和横向均匀磁化的有限长永磁棒内外轴线上的磁场分布.如果永磁棒的磁化方向既不是轴向，也不是横向，我们可以将其磁化强度矢量沿轴向和横向分解，然后将轴向分量和横向分量各自激发的磁场叠加起来，即得沿任意方向均匀磁化的永磁棒在轴线上的磁场分布.

将1.1节里的β1和β2用1.2节里的物理量L，R和z表示

代入式(2)和(3)，将轴向均匀磁化永磁棒轴线上的磁感应强度及永磁棒内外轴线上的磁场强度表示为

(8)

(9)

其中式(9)的上、下式分别代表永磁棒内、外轴线上的磁场强度.

如图6所示，设一般情况下永磁棒的磁化方向与其轴的夹角为φ.以永磁棒的轴为z轴，以横向磁化方向为x轴正方向，可得永磁棒磁化强度矢量的横向和轴向分量分别为

图6 永磁棒沿任意方向磁化

Mx=Msinφex

(10)

Mz=Mcosφez

(11)

将其分别代入式(6)、式(7)、式(8)、式(9)，并将得到的磁感应强度或磁场强度重新组合，可得沿任意方向均匀磁化的永磁棒轴线上的磁场为

2 无限长永磁棒在全空间中的磁场分布

2.1 轴向均匀磁化

令式(2)中β2=0，β1=π，并依据磁场的环路定理，可得无限长永磁棒轴向均匀磁化时轴线上的磁感应强度和磁场强度分别为

H=0 (棒内外)

(12)

(13)

即无限长永磁棒沿轴线均匀磁化时，其内部磁感应强度是均匀的，外部磁感应强度为零，磁场强度在全空间均为零.

2.2 横向均匀磁化

如图7所示，假设存在两根均匀带等量异号磁荷的永磁棒，圆心间的距离为dx.永磁棒的磁荷体密度各自为±ρm.重叠部分可视为无磁荷，下面求这种组合体的磁荷面密度分布.

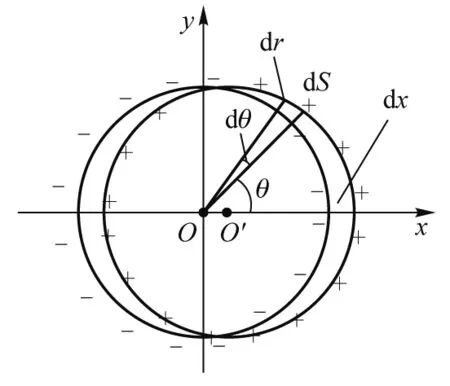
图7 均匀永磁棒磁荷叠加示意图

取如图7所示的一块顶角为dθ的三棱柱，则三棱柱在两圆柱间的部分可视为底面积为dS，高为dr的四棱柱，其所带的磁荷为：dqm=ρmdSdr，又由dr=dxcosθ，可得该处磁荷面密度为

与式(5)对比可知，当ρmdx=J时，两根均匀带等量异号磁荷的无限长永磁棒叠加后的磁荷分布与横向均匀磁化的无限长永磁棒的磁荷分布一致，从而这两种模型产生的磁场也一致.

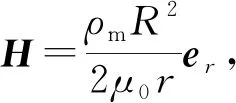
如图8所示，P点与带正、负磁荷的永磁棒的轴线距离分别为r+和r-，则该处的磁势为

因为r-=r++dr，且dr<

考虑到dr=dxcosθ，r+≈r，ρmdx=J，于是有

由磁势可求得永磁棒外距轴线r处的磁场强度为

磁感应强度为

图9 P点在永磁棒内部

磁感应强度为

这表明，横向均匀磁化的无限长永磁棒内任意一点的H和B都相同，均匀分布，且与棒的半径无关.在轴线上，直接令式(6)和式(7)中的L→∞会得到相同的结果.

综上可得，无限长永磁棒沿横向均匀磁化时，距其轴线距离为r，且与磁化强度M夹角为θ处的磁场强度和磁感应强度分别为

(14)

(15)

2.3 一般情况

无限长永磁棒沿任一方向均匀磁化时，与1.3节一样，我们将其磁化强度矢量沿轴向和横向分解，如图6所示.轴向磁化分量激发的磁场由式(12)、式(13)给出，横向磁化分量激发的磁场由式(14)、式(15)给出，两者的合成给出永磁棒内外的总的磁场分布.

将式(10)、式(11)代入式(12)、式(13)、式(14)、式(15)，并将得到的磁场合成，得无限长永磁棒沿任一方向均匀磁化时在全空间的磁场分布为

(16)

(17)

其中：ex=cosθer-sinθeθ.由式(16)和式(17)可知，沿任一方向均匀磁化的永磁棒，其内部磁场强度和磁感应强度都是均匀的，且与永磁棒的半径无关，外部的磁场强度和磁感应强度均只与磁化强度的横向分量有关，与轴向分量无关.

3 结语

本文分别计算了沿轴向和横向均匀磁化的有限长永磁棒轴线上的磁场分布，以及沿轴向和横向均匀磁化的无限长永磁棒在全空间的磁场分布，并利用叠加原理，给出了沿任意方向均匀磁化的有限长永磁棒在轴线上的磁场以及无限长永磁棒在全空间的磁场.