如何在“电动力学”课程中统一描述光的传输模型

陈培锋

(华中科技大学 光学与电子信息学院，湖北 武汉 430074)

在光电信息科学与工程专业教学中，传统的光传输理论主要包括“几何光学”和“波动光学”课程.“电动力学”课程传统上不属于光电信息科学与工程专业的先修课程，但是随着光电科学技术的发展，特别是光电材料领域的快速发展，光的传输过程仅仅依靠“光线”和“标量波”理论已经无法满足要求，因此描述“电磁波”理论的“电动力学”课程，已经逐渐成为光电信息科学与工程专业的必修课程.我校从2009年起逐渐开始推广“电动力学”课程在“光电信息科学与工程”专业的教学.实践证明，在光电信息科学与工程专业开设“电动力学”课程，对于学生综合理解学科热点、前沿问题的理论基础问题具有良好的效果，同时对于学生综合理解传统“光线”和“标量波”理论模型具有重要的意义.

1 理解光传播的不同分析模型之间的区别与联系对光电专业学生很重要

传统的基础理论物理课程逻辑自成体系，不可能关注到各个应用学科领域的具体要求.因此探索电动力学理论与光电信息专业知识的结合，掌握电动力学基本理论方法在本学科的具体应用，对于提高学生的学习热情，提升学生的学习效果非常重要.经过实践，我们认识到在“电动力学”课程中理解光传输理论中不同分析模型之间的联系，对于光电专业的学生很重要.

我校光电信息科学与技术专业，学习描述光传输的课程，包括“物理光学”“应用光学”“激光光学”“光纤光学”等多门课程.在这些课程中，光会以各种不同的模型出现.例如，在“应用光学”课程中，光是直线传输的没有宽度的“光线”；在“物理光学”课程中，光是无限宽的“平面波”；而在“激光原理”课程中，光是有限宽度的“高斯光束”；在“光纤光学”课程中，光又是可在光纤中传输的各种“模式”.那么，“光”究竟是什么呢？如何统一认识这些不同的光模型，需要且可以在更基础的电动力学中统一解决.

正确理解这些模型的关系和区别，对于学生今后在专业发展中理解如何应用这些模型非常重要.例如“应用光学”和“物理光学”都可以描述光在真空中的传输，那为什么有时候用“应用光学”知识设计光学系统，而在另一种场合却要采用“物理光学”的知识改进光学系统的分辨率呢？这对于学生理解例如“光刻机”这样的复杂光学系统的设计是必须的.

上述这些知识，不是传统“电动力学”课程内容，但却可以通过“电动力学”课程的进一步演绎加以论述.

2 在“电动力学”课程中介绍“光线”的推导和应用范围

“平面电磁波”是“电动力学”课程介绍光传输的标准内容.我们的实践表明，在介绍平面电磁波知识时，适当推导“光线”的近似和“高斯光束”近似，可以使学生很好地理解后续关于光学理论之间的联系，理解在实际光学系统设计中不同理论应用的场景.

在“应用光学”中，光是直线传输的没有宽度的“光线”；在“物理光学”中，光是无限宽的“平面波”；而在“激光原理”中，光是具有有限宽度的“高斯光束”.这3种模式同样都是用来描述光在自由空间传输的模型，学生最不容易理解的就是光好像可以被人们任意假设.实际上在“电动力学”课程里一般只讲平面波的解，也就是一般只给出了“物理光学”所涉及的模型.如果在此同时，能够用简单的方法介绍“光线”和“高斯光束”的来源，就会发现实际上这3种解都只是在不同条件下电磁波传输的近似模型，只是在不同的条件下采用了不同的模型.采用这种简述方法，一般只需要2个学时，基本就可以使学生理解“应用光学”、“物理光学”和“激光光学”之间的内在联系.

3 “光线”的简单推导

直接从麦克斯韦方程组开始[1]，考虑各向同性介质中一般的时谐波[2]:

(1)

式中E0和H0代表r处的复矢量，实部代表场.

E0=eeik0n(s·r),H0=heik0n(s·r)

(2)

式中e和h是常复矢量.对于真空中单色时谐球面波，则有

E0=eeik0r,H0=heik0r

(3)

其中r是距电偶极子所在的坐标原点的距离.这里e和h不再是常矢量，但是在距光源足够远的地方(r>>λ0)，这些矢量就与k0无关.这些例子提示我们，在距离场源较远的区域，场的更普遍类型可表成如下形式：

E0=e(r)eik0S(r),H0=h(r)eik0S(r)

(4)

其中S(r)为“光程”，是位置的实标函数，而e(r)和h(r)是位置的矢函数，它们一般可能是复数.以式(4)作为麦克斯韦方程组的试探解，即可得到e、h和S的一组关系式.可以得到：

(5)

(6)

(7)

(8)

光频的k0非常大，只要方程右边1/ik0的乘积因子不是特别大，就可以把它们统统略掉，这时我们可以只注意式(5)和式(6)，因为以S标乘这两式就得到式(7)和式(8).式(5)和式(6)可以看作是e、h的6个直角坐标分量的6个联立线性齐次标量方程.只有满足一致性条件(其结合行列式为零)，这些联立方程才有非零解.从式(5)和式(6)中消去e或h，即可直接得到这个条件.以式(6)中的h代入式(5)，得到

(9)

式中第一项因式(7)而为零，而由于e不是处处为零，因而方程化为

(S)2=n2

或

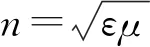
通过式(5)—式(8)可以看到，在几何光学近似下，每一点处的电场e、磁场h和波阵面法线方向S相互垂直.由此可知，在几何光学近似下，每一点处的坡印廷矢量方向一定与波阵面法线方向相一致，也就是说光波的能量一定沿波阵面法线方向传输.这就是“光线”的基本特征.可以把几何光线定义为几何波阵面S=常数的正交轨线，把光线看作是一些定向曲线，它们的方向处处都与平均坡印廷矢量的方向相重合.

进一步，还可以证明电能密度和磁能密度的时间平均值〈we〉和〈wm〉相等，即

(10)

在几何光学的精度范围内，电能密度和磁能密度的时间平均值是相等的.

坡印廷矢量的时间平均值为

〈S〉=v〈w〉s

(11)

上述证明过程特别有意义的是要求式(5)—式(8)右边括弧内的乘积因子与1/k0相比不是特别大.这个条件实际上要求，在波长尺度范围内场和介质的变化不明显.理解了这一条件，学生就很容易理解为什么可以利用以“光线”作为基础的几何光学进行光学系统的设计，但在焦点处则必须利用波动光学分析焦点附近的光场变化.而理解了几何光学和波动光学理论模型的适用范围，更有利于理解在开发复杂光学系统中的不同阶段所采用的理论模型之间的关系.由此可以体会物理基础对于专业课程的认知是非常重要的.

4 “高斯光束”的特性说明

高斯光束是激光光学的基础，为了反映激光光学的新进展，《电动力学》教材已经将高斯光束的推导引入了最新的版本[2].根据个人的教学经验，光电信息科学与工程相关专业可以选择讲授这部分内容，对于学生理解激光束以及由此派生出的特殊光束(例如贝赛尔光束等)很有帮助.

高斯光束的推导可以从亥姆霍兹方程开始[2]：

2u+k2u=0

(12)

其中u为电磁波的任一时谐波直角分量，取

u(x,y,z)=E0(x,y,z)e-ikz

(13)

取振幅E0满足缓变振幅条件，可以推导出自由空间中传输的一种“高斯光束”特解[2,3]：

(14)

其中u0、w0为常数.

(15)

(16)

(17)

根据实际教学经验，在上述高斯光束推导的基础上应该向学生强调以下几点：

(18)

当w0→∞时，θ→0，则光束趋向于平面波.因此上面的结果实际上说明对于有限口径的光束，总存在由于衍射带来的光束发散，这是波动光学的基本特征.

2) 这是一个近似解，近似条件为忽略了∂2E0/∂z2项.这个条件除了极小的聚焦点处外，一般都满足这个条件.

3) 光束波前是一个近似的半径为R的球面，但球面中心是不固定的，在较远处的球面中心为原点.

5 总结

平面电磁波是“电动力学”课程的标准教授内容，如果在此基础上介绍“光线”和“高斯光束”的传输特性，就会使学生对这些光束传输的基本模型有一个整体的理解.学生能够通过这些内容理解不论是平面波，还是光线或高斯光束这些模型都可以出自麦克斯韦方程组，只是存在不同的近似条件，也就意味着在不同的条件下成立.因此通过“电动力学”课程就可以将各种光传输有关的课程之间的联系打通[4,5].当然要做到这一点是有困难的，因为“电动力学”课程本身就是非常难学的课程，在这个基础上再赋予更多的教学内容，需要在教学方法上下功夫.但我们认为增加上述教学内容对光电信息专业学生是有必要的.实践证明，通过不断改进，“电动力学”课程是可以在光电信息科学与工程专业本科学生的培养过程中发挥更大的作用的.