分子动力学方法中速度标度因子的推导

齐 楠，王圣军

(陕西师范大学 物理学与信息技术学院，陕西 西安 710119 )

计算机模拟现已成为实验方法和理论研究以外的一种有效的物理研究手段，而分子动力学方法作为一种确定性模拟方法，其在计算机模拟中显得尤为重要.在许多计算物理教材[1-3]中，对于模拟由大量粒子组成的系统，分子动力学方法都是尤为重要的内容.

分子动力学方法是指利用每个分子的运动方程通过统计方法来计算系统的性质.其以粒子间的相互作用为出发点，在计算机上求解运动方程的数值解.在这一求解过程中，涉及的物理量包括能量E、力F、质量m、温度T、位置r、时间t、速度v等.然而，在系统中，这些物理量的大小在国际单位制下具有过于小的数量级，这不利于在计算机上进行运算.于是，在分子动力学方法中，首先需要对物理量重新标度.这样，对于重新标度后的物理量的大小，其数量级在1附近，并且能够得到形式简单的运动方程.

在分子动力学模拟中，重新标度的方法是理解分子动力学方法的重要环节.在重新标度的过程中，需要考虑系统的运动特征，这具有一定的物理内涵.然而其在多数教材中显得过于简略，例如没有介绍时间单位的物理内涵.另外在模拟过程中标度因子是一个尤为关键的量.在微正则系综中，给定初始位置和初始速度以后，在系统趋衡过程中需要调节速度，使系统的温度达到给定系统的温度.对速度的重新标度通过标度因子实现.然而，与之相关的书籍[1-3]往往直接给出了标度因子的数学表达式，没有明确地指出如何合理地对其进行推导.这使得分子动力学模拟的原理难以被学生充分理解.

接下来，本文将对标度因子的表达式予以推导，并且对物理量重新标度的方法给出合理的说明.这样会得到重新标度的运动方程、物理量和标度因子，帮助初学者掌握完整的模拟原理，以便于在面对新的情景时推导相应的公式开展计算机模拟.

1 重新标度前的公式

在分子动力学模拟过程中，首先要设定模拟所采用的模型.这里考察最基本的情况微正则系综，并且采用单原子粒子系统，分子间的相互作用势采用Lennard-Jones势.系统的哈密顿量表示为

(1)

其中分子间相互作用势u(rij)为

(2)

这里rij是粒子i与粒子j的距离，ε和σ是两个参数.

由于统计物理系统的特性，精确地控制初态是困难的.模拟过程中人为设置的系统初态不会具有所要求的能量，并且系统的状态不是一个平衡态.为了使该系统的能量达到一个确定值，在系统趋衡的过程中调节系统能量，使其逐步达到所要求的状态.热力学平衡状态下该系统具有给定的温度T，根据能量均分定理有

(3)

这里kB是玻耳兹曼常量.

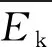
(4)

(5)

从而得到标度因子为

(6)

为了进行计算机模拟，通常对系统进行无量纲化处理.教科书中的速度标度因子都是在无量纲化的模型中给出的.通常它的形式与式(6)的形式并不相同，并且它依赖于无量纲化的处理方式.

2 物理量的重新标度

粒子i的牛顿运动方程为

(7)

(8)

于是

(9)

其中rij=ri-rj.对于计算机模拟，需要用到式(6)、(7)、(9).

这里需要对物理量进行重新标度，进而把分子动力学模拟中用到的物理量变成无量纲的量，使运动方程具有简洁的形式.

另外，如果在模拟中仍然采用国际单位制，那么粒子的质量m、位置r和基本时间步长h的数量级均很小，可能会导致舍入误差的产生.于是，对物理量进行重新标度的另一个原则是：避免过于小或过于大的数量级出现在计算机模拟中[4].

为了得到具有简洁形式的运动方程，本文并不是直接对力学中常用的基本物理量进行重新标度，再导出其它物理量.在分子动力学模拟中，选取一些反映相互作用和运动特征的物理量，首先对它们进行恰当的重新标度.进而把这些重新标度的物理量作为新的基本物理量[5,6]，由新的基本物理量导出其它物理量、标度因子和运动方程.

现在对物理量重新标度，并以星号*表示重新标度后物理量的数值.从后文可以看到，一方面物理量的数值的数量级不会远远偏离1，另一方面运动方程经过了无量纲处理.

根据式(2),容易得到-ε是分子间相互作用能的最小值，这个最小值在r=21/6σ处.参数ε决定了两个粒子处于平衡位置的相互作用能，参数σ决定了两个粒子处于平衡位置的距离.规定σ为长度单位，ε为能量单位，得到变换关系:

l=l*σ

(10)

E=E*ε

(11)

考虑粒子i与粒子j间相互作用的时间.在其质心系中，将两粒子所构成的系统的总能量E表示为E=aε，则a为一个无量纲的参量.由该系统能量守恒[7]得到

(12)

(13)

上式为系统运动时长t关于两粒子间距离rij的微分表达式.容易得到两粒子间由最小距离r1处首次运动到最大距离r2处经历的时间T[7]为

(14)

图1 的数值模拟结果

粒子间相互作用的时间也可以从以下的角度考虑.当一个粒子的振动范围很小时，可以对系统中其它粒子对该粒子的作用做线性近似.考虑粒子i在单个粒子的势场中的运动.粒子i的位置用ri表示，考察粒子i的运动周期.由式(8)，粒子i在势场中受到的作用力f(ri)为

(15)

则r0=21/6σ处是粒子i振动的平衡位置.将f(ri)在r0处做泰勒展开，保留线性项，得到

(16)

其中x=ri-r0.于是粒子i的牛顿运动方程为

(17)

(18)

这里时间单位中包含一个常数48.它的作用是把相互作用力代入牛顿第二定律的时候，得到的运动方程形式更加简单.

(19)

于是m*=48，即重新标度后质量m具有m*=48的数值大小.

由式(7)、(9)、(10)、(18)，得到重新标度后的牛顿运动方程，其表示为

(20)

(21)

这里h*是重新标度后的基本时间步长.

(22)

(23)

由式(11)、(23)，重新标度后平均动能表示为

(24)

由式(6)、(22)、(24),重新标度后标度因子β表示为

(25)

这里得到的标度因子与相关书籍中的结果是一致的[1-3].当导出了所有相关的公式以后，为了简便，忽略所有无量纲物理量的*号.

3 双原子分子与量子分子动力学方法

原则上，由大量粒子组成的系统都可应用分子动力学方法模拟.这个系统包括的不只是点粒子系统，也包括具有内部结构的粒子组成的系统.如果按照系统所遵循的运动规律不同，分子动力学方法可分为经典分子动力学方法和量子分子动力学方法.经典分子动力学方法中，系统中每个分子各自都服从经典运动定律.有时必须考虑系统中的量子效应，这需要用量子力学来处理.这种考虑微观组态变化影响的分子动力学模拟称为量子分子动力学模拟，也称为从头计算的分子动力学模拟或第一性原理计算[8].量子分子动力学方法处理的是多电子的薛定谔方程:

Hψ(r,R)=Eψ(r,R)

(26)

其中，r和R分别代表所有电子和原子核的坐标[8].基于密度泛函理论的第一性原理的计算方法由Car与Parrinello于1985年提出并用于实际计算.在过去的几十年中，分子动力学模拟发展很快，并在许多领域得到了广泛的应用[8,9].

根据分子动力学方法的基本步骤，系统中相互作用势函数的确定尤为关键.在分子动力学方法中，通常是基于经验数据和经验规律来选取势函数.除了常用的Lennard-Jones势，还有Morse势、Kihara势、谐振子势、偶极子势等.其中，Morse势极好地描述了双原子分子的振动，其数学形式如下[10]:

V(r)=D(e-2αx-2e-αx)

(27)

在薛定谔方程的数值求解中，通常以埃为单位来度量所有的长度，以电子伏为单位来度量一切能量[11].在这样一种单位制下，方程中的物理量和常数具有较好的数量级.在所谓的量子分子动力学方法中，也可以类似地对系统做无量纲化处理.只需要对长度和能量分别进行重新标度.这种无量纲化处理方式与前文所述是一致的.

因此，确定好势函数和运动方程后，总是可以按照本文的无量纲化处理方式对物理量进行重新标度，使运动方程更加简洁.值得注意的是，其中对基本物理量的选取和重新标度依赖于具体的物理模型，这具有一定的物理内涵.

4 结语

本文首先给出了趋衡过程中速度标度因子在国际单位制下的数学表达式.然后，说明了如何把物理量重新标度得到无量纲公式，使得在模拟中计算更加方便.本文通过物理量的重新标度，给出了时间单位的物理意义，并且给出了教材中常用的标度因子相应数学表达式的推导过程.文中的方法可以帮助初学者掌握完整的模拟原理，以便于在面对新的情景时推导相应的公式开展计算机模拟.