一维非定常流体力学数值模拟
付智豪,余 聪
(中山大学 物理与天文学院,广东 珠海 519082)
数值模拟在天体流体力学中具有重要意义,传统的计算流体力学(Computational Fluid Dynamics,CFD)包括有限差分法和有限体积法等,而后又发展了诸如格子玻耳兹曼 (lattice Boltzmann method,LBM)和离散玻耳兹曼(discrete Boltzmann method,DBM)等计算方法[1-10].Riemann问题是CFD中的基本问题,即解决初始间断下物理量的演化过程.此类方法除了可以有效的处理间断解,也能自洽的求解待求区域内光滑变化的物理量,十分适合研究具有复杂空间结构和时间结构的流场.对于激波管内的Riemann问题,可求解出其理论解,但缺点是在复杂的初始条件下,模拟常常需要耗费大量的时间.在实际研究中,人们常常无法求得理论解析解,这时可以采用近似解的方法代替理论解.Roe通量差分裂格式作为CFD中最广泛使用的格式[2],适用性较广,且精度较高,可以此研究不同初始条件下问题解的情况.本文仅考虑理想情况下的流体,从一维Euler方程出发,推导了Riemann问题下速度、密度及压力的理论解,然后介绍了Roe通量差分裂格式及算法,以Sod、Lax及Shu-Osher激波管为算例检验算法的有效性,并在最后介绍了拓展至高维流体运动的方法.
1 理论解
1.1 控制方程
流体的运动十分复杂,但此处仅考虑无黏性的理想流体运动,且为了简化问题只考虑一维情况,于是可采用守恒型的一维Euler方程进行描述[1]:
(1)

1.2 Riemann问题的解
在求解方程组(1)时,如果设置密度、速度和压强的初值为间断型条件,那么流体物理量的演化会出现激波、稀疏波和接触间断的现象,此类问题便称为Riemann问题.如圆柱管内有一薄膜,当两侧压强差大到使其破裂,会形成冲向一侧的激波,同时在另一侧形成膨胀的稀疏波,二者间存在一个接触间断区.激波即密度、压强和速度在波阵面上发生突变的压缩波.
Riemann问题是CFD中的核心问题之一,求出其精确解对解决流体运动具有重大意义.有限体积法便是将计算区域划分为若干个区域,将每个小块的边界当作间断面,进行Riemann问题近似求解,最终合并区域得到整个流场的运动.对于不同的初始条件,其解可分为5种情况[4]:1) 左激波+接触间断+右激波;2) 左稀疏波+接触间断+右激波;3) 左激波+接触间断+右稀疏波;4) 左稀疏波+接触间断+右稀疏波;5) 左稀疏波+真空区域+右稀疏波.
以情况2为例,对应于管内薄膜破裂,图1给出解的x~t图.Ⅰ和Ⅱ区为未受扰动区域,分别对应稀疏波波前区域和激波波前区域,满足初始条件.Ⅲ区对应于稀疏波过后的波后区域,Ⅳ区对应于激波过后的波后区域,3条实线间的Ⅴ区对应于稀疏波区域.其中在Ⅲ区和Ⅳ间的虚线表示接触间断,Ⅳ区和Ⅱ间的实线表示激波间断.

图1 左稀疏波+接触间断+右激波
1.3 数学解释
若将式(1)改写为拟线性形式[4]:
(2)
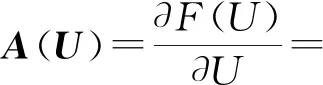

A(U)=L-1ΛL
(3)
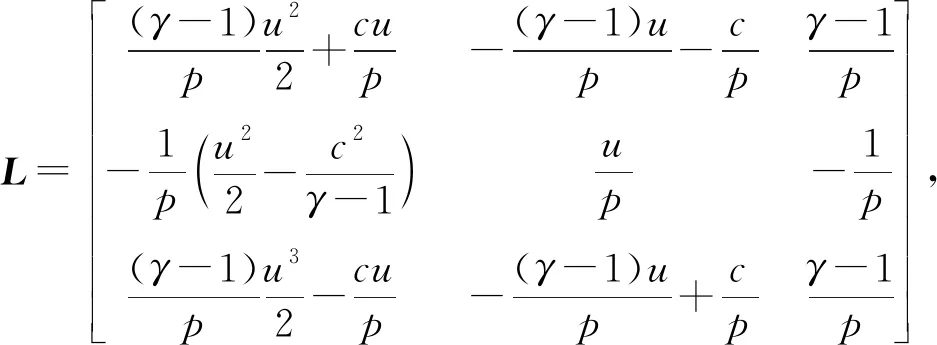


(4)

1.4 等熵流动
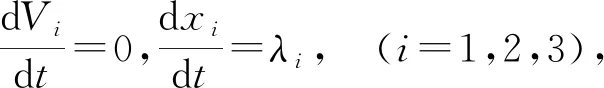
(5)
若流体运动无黏性且满足绝热条件,即等熵流动[4],能量方程可用
(6)
代替.γ为绝热指数,于是由式(5)得
(7)
其中u为流体的运动速度,c为声速.第1式为描述特征线的方程,第2式为特征线上的不变量,又称Riemann不变量,上下标分别对应向右传播和向左传播.
1.5 激波间断
实际上的激波具有厚度,但数值仅是气体分子自由程的数倍,故数学上可近似处理成为间断.考虑流体积分形式的守恒型方程,设激波从左往右运动,运动速度为Z,左侧物理量为(u1,p1,ρ1),右侧物理量为(u2,p2,ρ2),则间断处满足Rankine-Hugoniot(激波)跳跃关系式,简称R-H关系式[4].
(8)
1.6 具体求解

(9)

(10)
于是激波、稀疏波前后速度-压力关系可写成统一形式:
(11)
其中下标i对应波前区域的物理量.式(9)、式(10)相加得
u1-u2=f(p0,p1,ρ1)+f(p0,p2,ρ2)=F(p0)
(12)
若p1>p2,当p0>p1时,中间区域压力大于两侧,说明两侧均为激波,对应情况1;当p1>p0>p2,中间压力比右侧大比左侧小,说明右侧形成激波,左侧形成稀疏波,对应情况2;当p2>p0,中间压力比两侧都小,说明两侧均为稀疏波,对应情况4;当p0≤0,由于实际上压力不能小于零,故为真空区,对应情况5.若p1 图2画出了F(p)随p的变化关系,可见其为单调递增函数,于是p之间的大小关系等价于F(p)之间的大小关系.故流体的演化情况,也可先求出F(p1)、F(p2),再与F(p0)=u1-u2比较进行判断. 图2 (1,0,1)和(0.125,0,0.1)初始条件下F(p)与p的关系 由式(12)求解出中心区压力p0后,代回式(9)或式(10)可求解出中心区速度u0.于是激波后区域内的密度为 (13) 激波间断的速度为 (14) 稀疏波后区域内的密度,由绝热过程公式可得 (15) 波头速度及波尾速度为 (16) (17) (18) (19) (20) Riemann问题虽然具有解析解,但实际运用中计算量较大,处理问题效果不是很好.若采取近似解的方法,不仅能够精确描述流体运动,编程效率也能大大提高,下文便介绍近似解的Roe方法. 编程算法上采用有限体积法,对式(1)空间导数部分采取一阶差分[8]: (21) (22) 得 (23) Roe给出了常矩阵构造方法[2],先由左右点值求得平均值: (24) (25) (26) (27) (28) (29) ε为设置参数,在此取为10-7. 为了检验Roe算法的有效性,对以下经典算例进行了数值模拟,计算与画图均采用Matlab语言[8]. Sod激波管,由两个不连续分隔的恒定状态组成,属于经典的Riemann问题[3,9].图3展示了Roe格式下的数值解,并以理论解检验算法精度.发现其数值解与理论解值相符,但在间断区域内过渡平滑,这是由于算法精度不够高导致的. 图3 Sod激波管 如图3所示,位于x=0.18的物理量均存在着一个突变,这对应于一个向右传播的激波.在与激波运动相反的方向,由于右侧分子的减少,流体向外膨胀,形成了一个向左传播的稀疏波.-0.12 同Sod激波管一样,也是由两个不连续分隔的恒定状态组成,但初始条件不同.图4展示了Roe格式下的数值解,并以理论解检验算法精度.其数值解与理论解相符,间断处的过渡是由于算法精度所限. 图4 Lax激波管 该问题能够很好地测试算法捕捉平滑流动下激波相互作用的能力.初始条件是一个强激波,初始位置在x=-0.4,传播到密度呈正弦变化的背景介质中.图5展示了用Roe格式求解出的密度、速度和压强的位置分布,其中密度的位置分布与文献[9]中求解出的趋势一致,说明Roe格式算法具有较强的适用范围. 图5 Shu-Osher激波管 对于高维情况,只需对Euler方程进行改写,然后采用相应的Roe通量差分裂格式[9]及差分化方程,便可进行高维流体模拟计算.如3维Euler方程可写为 (30) 则拟线性形式为 (31) 对于x方向,有 (32) 当w=0时,方程对应于2维流体模拟;当v=w=0时,方程对应于1维流体模拟. 非线性的流体偏微分方程中间断解是物理中十分具有挑战的问题,能够对激波精细结构进行有效追踪和捕捉的算法是当前流体力学的热点之一.本文从一维Euler方程推导出其Riemann理论解,揭示了流体内的激波、稀疏波和接触间断等现象物理本质.为了进一步描述不同情况下的流体运动,文章采用了Roe格式,再次对Riemann问题求解,以检验其有效性.通过比较,发现一维下Roe格式与理论解符合度较高,能很好地描述激波管内物理量的演化过程.由此认为Roe格式是很好的近似解,继而将该格式拓展至2维和3维形式.而且Roe格式的简单形式使得其不仅能解决非定常的Euler方程,在考虑磁场效应后,通过对方程的改写,也能轻易的拓展到磁流体动力学的计算[9].而且采用更高精度的激波捕捉格式,如TVD、MUSCL和WENO等[3,4],Roe格式求解与理论解几乎无异.正是因为Roe格式在求解流体动力学性质上的优越性,使得其成为当前天体物理应用数值方法的主流方法. 本文仅考虑了理想状态下的流体运动,但实际中,由于微观粒子的复杂相互作用,在宏观上存在着不同相与组分的离子界面,比热、黏性系数、热传导率等不再保持为常量,基本平衡方程不再满足,出现了非平衡的动力学及热力学效应.采用NS和Euler建模在解决上述问题时存在一定的局限性,但近来发展的DBM方法从多尺度建模,不仅提高了对激波精细结构的描述,而且在深度和广度上都超越了原有建模[11].


2 Roe通量差分裂格式
2.1 方程差分化

2.2 基本原理

2.3 Roe格式


2.4 熵修正
3 数值算例
3.1 Sod激波管
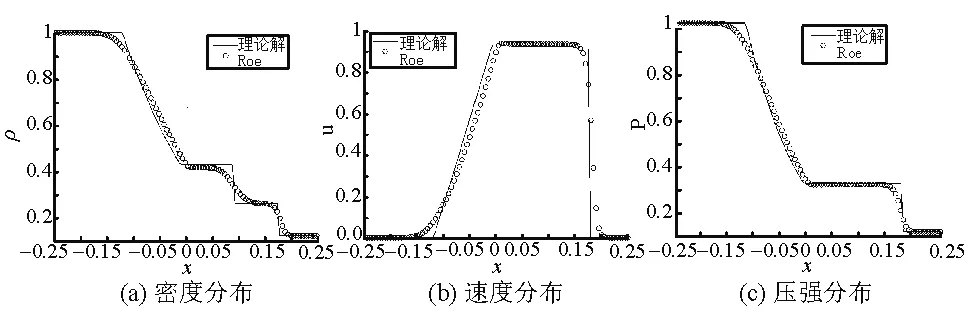

3.2 Lax激波管


3.3 Shu-Osher激波管


4 高维拓展




5 结束语

