静磁外部球谐多极矩展开

余 天，林 方，姚 欣，齐建起，张志友，聂 娅，王 磊，朱建华

(四川大学 物理学院,四川 成都 610065)

在本科物理及相关专业培养中，静磁场是“电磁学”和“电动力学”课程教学的基本内容.在教学中静磁场通常采取与静电场进行类比的方式展开.例如，在介绍无源单连通场域的静磁场时，常类比静电场引入磁标势，进而将此类静磁问题化归为已在静电学中深入讨论过的静电拉普拉斯方程边值问题.然而在类似静电多极矩展开的静磁多极矩展开教学中，国内教学资料通常仅限于介绍直角坐标表示的静磁矢势多极矩展开[1-4]，少见与静电球谐多极矩展开呼应的静磁球谐多极矩展开介绍，也鲜有关于磁标势在静磁多极矩展开中应用的讨论.

多极矩展开可有两种情况：场点位于有限源区外部的外部多极矩展开和场点包围在源区内部的内部多极矩展开[5].实际教学中主要介绍外部多极矩展开，给出的一般适用情况为：源分布在有限空间中其线度R远远小于待求场点到源(中心)的距离，此时取原点在源分布中心附近，可将远源场点处电磁势函数展为收敛级数.静磁外部球谐展开即在球坐标系下将满足上述条件的远源场点处静磁场的势函数展为关于场点距离幂和球谐函数的收敛级数.本文综合国外相关探讨[5-7]先介绍静磁标势的外部球谐多极矩展开，再分析静磁矢势的外部球谐多极矩展开.其中静磁矢势外部球谐多极矩展开的分析采用了2种不同的方法： 1)基于远源场点处的磁场既可由磁标势表示也可用磁矢势表示，从静磁标势的外部球谐多极矩展开出发分析得到惯用的静磁矢势外部球谐多极矩展开表示；2)从远源场点的磁矢势出发，借由德拜势表示的静磁矢势引入角动量算符直接获得静磁矢势外部球谐多极矩展开惯用表示.

1 静磁标势的外部球谐多极矩展开

考虑静磁外部多极矩展开时，电流源总是分布在原点附近的有限源区空间V′中，而且待求场点在源区外部，因此待求场域总是单连通空间，在其上可以引入静磁标势φ(r)，有

H(r)=-∇φ(r)

(1)

对于磁导率为μ的简单介质，静磁场相关的麦克斯韦方程组和本构关系分别为：

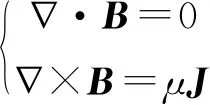
(2)

B=μH

(3)

由此得到场点r处的磁感应强度B(r)与该点处的静磁标势φ(r)满足关系：

B(r)=-μ∇φ(r)

(4)

注意到有

∇2(r·B)=r·∇2B+2∇·B=r·∇2B

(5)

我们可得到关于标量(r·B)的泊松方程：

∇2(r·B)=-μr·(∇×J)δ(r-r′)

(6)

其形式解不难类比于静电标势泊松方程的库仑积分而写出，即

(7)

(8)

(r≫r′) (9)

其中Ω=(θ,φ)和Ω′=(θ′,φ′)分别代表场点r和源点r′坐标的角量部分.将其代入静磁标势方程并对场点距离直接积分得到

(10)

其中积分系数：

(11)

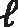
2 从磁标势出发求静磁外部球谐多极矩展开

数学上远源的单连通场点r处的静磁场B(r)既可借由磁标势φ(r)刻画也可等效由磁矢势A(r)表示：

-μ∇φ(r)=B(r)=∇×A(r)

(12)

基于此我们由静磁标势的外部球谐多极矩展开来求磁矢势外部球谐多极矩展开形式.

上式左侧给出

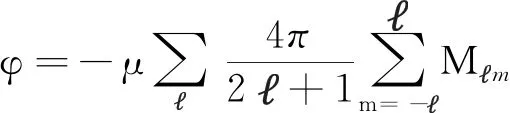
(r≫r′) (13)

我们注意到球谐函数满足如下关系：

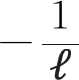
(14a)

(14b)

引入关于场点的角动量算符：

(15)

不难将式(13)改写为

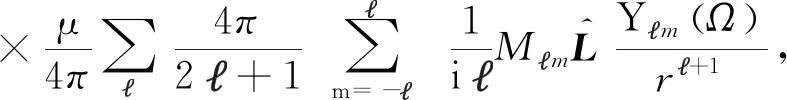
(r≫r′) (16)

换言之，我们找到了源区外部远源场点r处磁矢势的一种表示：

(r≫r′) (17)

这就是惯用静磁矢势外部球谐多极矩展开式.

3 静磁矢势的球谐多极矩展开的直接分析

磁标势的引入是有条件的，而任意场点都可定义磁矢势.故而直接求静磁矢势外部球谐多极矩展开具有更普遍意义.

源区V′中恒定电流J(r′)在其外部远源场点r处所激励静磁场对应磁矢势可以取为

(18)

类似于静磁标势情况容易将上式展为级数形式：

A(r)=

(r≫r′) (19)

为了由式(19)出发获得惯用静磁矢势外部球谐多极矩展开式，我们注意到任意矢量场总可分解为环向场(Toroidal Field)、极向场(Poloidal Field)和梯度场三部分[8-11].具体而言，我们总可将静磁矢势分解为

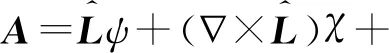
(20)

其中{ψ,χ}是德拜(P. Debye)在分析电磁辐射时最早引入的，故称为德拜势[8].对于静磁问题采用库仑规范，∇·A=0，通常是方便的.此时磁矢势无散，故上述分解中联系梯度场的标势总可取为零，φ=0.再考虑到磁矢势借由旋度联系磁感应强度，而极向场无旋对磁感应强度没有贡献，因此德拜势中不妨取χ=0.换言之，库仑规范下的静磁势可取为纯环向场，也即有

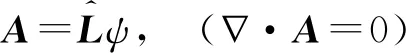
(21)

(22)

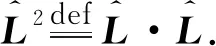
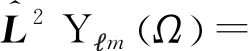
(23)

容易得到静磁矢势满足

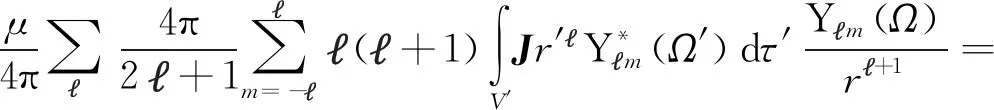
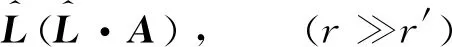
(24)

基于上式我们可以在磁矢势表述中引入角动量算符:

A=

(r≫r′) (25)

对于作用于源点的角动量算符

(26)

由球谐函数的完备性可知

(27)

具体到这里讨论的外部多极矩展开，因为场域与源区无重叠，故有

(28)

进而得到

A=

(29)

其中反映源分布特性的积分系数为

(30)

利用矢量运算关系：

J·(r′×∇′)=-(r′×J)·∇′

(31)

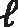
(32)

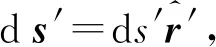
(33)

再由矢量运算关系：

∇′·(r′×J)=-r′·(∇′×J)

(34)

容易发现

(35)

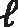
4 讨论与总结

首先，应该指出的是将电流密度J按球坐标分解并利用前述式(19)可直接得到静磁矢势形如静电外部球谐展开的级数表示.不难发现这一形式也满足按场点距离幂与球谐函数阶展为逐项递减的级数，并且级数中积分系数也只与源区电流分布特性有关，然而这一形式并不是惯用的静磁矢势外部球谐展开式.这主要是人们对磁场的认识最初是类比于电场采用磁荷观点解释磁现象所致.磁矢势可以追溯到1845年纽曼(F. Neumann)在借助安培的方法分析电磁感应定律时提出的“电动力学势”[12]，而基于磁荷观点，高斯(J. Gauss)在1839年已利用球谐展开分析得出地磁场主要源自地球内部[13].有鉴于静磁标势及其多极矩分析已有较多成熟应用，在磁矢势球谐多极矩展开中沿用基于静磁标势的球谐磁多极矩自然得到磁矢势球谐多极矩展开的惯用形式.其次，静磁标势外部球谐多极矩展开呼应了静电标势外部多极矩展开[14-16].尽管现在人们已经认识到激励磁标势的磁荷不是客观的物理存在，但仍可以在单连通无源区域建立起静磁标势与激励静磁场的恒定电流分布间的正确关系，即式(8).这区别于磁标势通常应用中只直接与磁荷相关联的情形，丰富了静磁标势的应用.第三，通常电磁学和电动力学中矢量分析的基础是亥姆霍兹定理，即任意矢量场总可唯一确定地分解为横场和纵场.利用德拜势分解矢量场进一步拓展了矢量场分解的内容，其核心在于任一横场还可以进一步分解为环向场和极向场.最后，介绍静磁外部球谐多极矩展开有助于向学生展示学科内分支间联系.例如，通常量子力学和原子物理课程中才涉及的角动量算符自然地出现在静磁矢势外部球谐多极矩展开中，不仅生动展现了算符作为运算工具的数学含义，也潜在的提示着我们磁矩与角动量间存在深刻联系.

本文讨论了静磁球谐多极矩展开，给出了静磁标势外部球谐多极矩展开和惯用的静磁矢势外部球谐多极矩展开.这些内容作为电磁学和电动力学课程的拓展，不仅有助于丰富矢量分析和多极矩分析的内容，深化学生对静磁标势及其应用的理解，还能展示物理学科内部不同课程间联系，提示我们进一步挖掘知识间的相互联系.