城市轨道交通网络特性与级联失效鲁棒性分析

杨景峰，朱大鹏，赵瑞琳

兰州交通大学 交通运输学院，兰州 730070

城市轨道交通由于其快捷、安全、舒适、环保和运量大的优点，逐渐成为居民日常出行的首选。目前我国已有45个城市正式开通城市轨道交通，部分城市已初步形成城市轨道交通网络（urban rail transit network，URTN）并向着网络化运营阶段迈进[1]，这就意味着一旦有站点由于外界破坏或者设备故障等原因发生故障，这种故障可能在网络中迅速传播扩散，造成严重的后果[2]，因此，对URTN进行系统的分析，研究其在突发事件下鲁棒性，对于保障其安全运营有着重要意义。

国内外专家学者针对城市轨道交通网络的拓扑特征和鲁棒性展开了一系列研究。Latora等[3]分析了波士顿地铁的网络特性；Zhang等[4]对北京、上海、广州三大城市的轨道交通网络的网络特性进行分析并对其面对随机故障和蓄意攻击时的网络鲁棒性进行了对比；曲迎春等[5]建立了城市公共交通双层网络模型，以北京和深圳轨道交通网络为例，对轨道交通网络的鲁棒性进行深入探究。级联失效的概念也被运用到轨道交通中来，刘朝阳等[6]建立了URTN级联失效模型，并仿真了北京城市轨道交通网络级联失效过程；蔡鉴明等[7]对长沙地铁网络的网络特征进行详细分析，并通过四项网络鲁棒性评价指标，分析了在级联失效情况下长沙市地铁网络的鲁棒性；王彬等[8]构建了网络级联失效模型，以北京市地铁网络为例，研究了在不同攻击策略下网络的级联失效抗毁性；张铁岩等[9]建立了基于耦合映像格子的地铁网络相继故障模型，分析了地铁网络故障的传播特点；赖强等[10]构建了城市公交网络的拓扑结构模型，分析了其鲁棒性并进行优化；张振江等[11]对铁路快捷货运网络在不同攻击策略下的级联失效鲁棒性进行深入研究。针对URTN的既有研究，专家学者们大多从网络拓扑特性和鲁棒性分别展开研究，有关结合网络拓扑特性、网络节点重要度且考虑级联失效现象的城市轨道交通网络鲁棒性的研究较少，因此，文中首先构建URTN的拓扑结构模型，然后结合度值中心性和中介中心性挖掘URTN的关键站点，最后以上海轨道交通网络为例，实证分析其复杂网络结构特性与级联失效鲁棒性。

1 URTN复杂特性分析

1.1 URTN拓扑结构建模

URTN中主要包含车站和线路，其拓扑结构构建方法主要分为三种：Space-L法、Space-P法和Space-R法，由于采用Space-L建模方法能从直观上反映城市轨道交通网络的连接形式，自然地反映网络的拓扑结构特性以及站点在网络中位置，故本文采用Space-L方法进行城市轨道交通网络拓扑结构建。

1.2 URTN复杂网络特征指标

（1）度、度分布及累计度分布

在URTN中，站点的度值指的是与其他站点连边的数量。度值是衡量站点特性最直观的物理量，通常站点度值越大，其在网络中的重要程度就越高。

式中，若站点i与站点j连通，则aij=1，否则aij=0。

对网络中所有站点的度值求平均，得到网络的平均度k：

度分布函数p(k)表示站点度值为k的概率分布，即度值为k的站点数目与网络站点总数的比值，可用来描述网络中站点度分布情况。累计度分布表征站点度值大于k的概率，计算如式（3）：

（2）最短路径长度

在URTN中最短路径l ij为从站点i到站点j所经历边的最小数目；平均路径长度L为站点对间最短距离的平均值；所有站点对之间最短路径长度的最大值为整个网络的直径D。

（3）聚类系数

站点聚类系数反应了网络中站点与邻近站点联系的紧密程度，是与其相邻的k i个站点之间实际存在的边数与最大可存在边数的比值，即：相应地，网络的聚类系数为所有站点C i的平均值：

（4）介数

站点的介数可以衡量站点在整个网络的作用及重要程度，经过站点i的最短路径越多，则该站点介数值越大，在网络上中影响力越大，计算公式如式（6）：

式中，σmn为站点v m与v n之间的最短路径的总数，σmn(i)为站点v m与v n之间的最短路径中经过站点v i的最短路径数目（m≠i≠n且1≤m＜n≤N）。

（5）连通度

除去上述网络特征指标之外，研究增加连接度参数，连接度作为网络的全局参数，连接度值越大就是证明整个轨道交通网络的节点连边数多，网络连通度高，城市轨道交通网络连接度计算公式如式（7）所示：

式中，e为轨道交通网络边数，N为网络总站点数，3N-6为轨道交通网络理论最大连边数。

2 站点重要性评价

挖掘URTN的重要站点对于站点的分级保护和资源优化配置十分重要，同时有利于增强网络的稳定性和鲁棒性。较多的专家学者采用单一的网络中心性指标对站点在网络中的重要性进行评价，然而单一指标通常无法全面衡量站点在网络中的重要程度。例如：度值可以衡量网络中站点的局部连接能力，但是忽略了其对非邻接站点及网络全局的影响。介数虽能较好地描述站点对网络全局的影响，但是并非所有重要站点都通过最短路径[12]。此外，由于城市轨道交通网络线路的不断增加，现有网络中的普通站点也许今后会成为连接不同线路的关键站点。

2.1 综合评价指标

根据文献[13]提出的方法，根据节点度和介数计算出节点介数中心性指标以及度中心性指标，基于以上指标，给出站点重要性的综合评价指标，即：

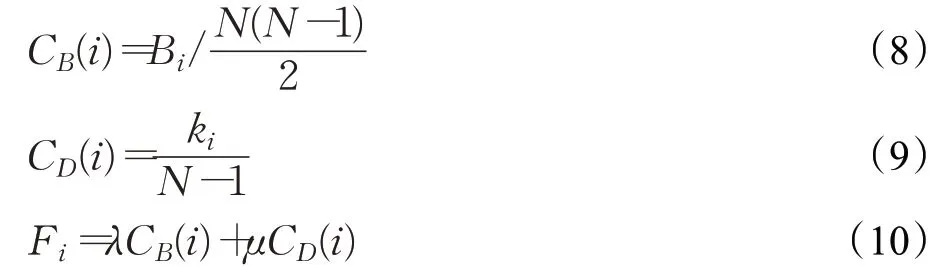
式中，Fi为节点i重要性综合评价指标；λ与μ为权重系数，且满足λ+μ=1。

2.2 权重系数的确定

为达到全面衡量站点在网络中重要程度的目的，需选择一组最优权重系数组合。通过设定不同λ和μ的值（λ,μ∈[0,1]）对站点重要性进行排序，根据重要性排序结果采用蓄意攻击对网络前5%的站点进行攻击实验，记录并分析每组λ和μ的组合下，网络效率E和最大连通子图大小S的值，选取使得E和S变化最大时对应的λ和μ值作为评价指标的权重系数，此时得到的权重组合能够最大程度衡量站点在网络中的重要程度。

3 URTN级联失效模型

URTN中的站点由于各类突发事件而发生故障时，其影响不仅限于故障站点，还会辐射到其相邻的站点甚至是整个网络。如图1所示，当某一站点发生故障时，其上原本负载的客流量以及尚未到达该站点的客流量将分配到其相邻的站点，导致相邻站点的负载发生改变，若相邻站点的负载超过其最大可承载容量，则会产生新的故障站点，从而进行新一轮的站点负载重分配过程，当发生多轮站点负载重分配之后，可能造成整个网络的部分或者全面瘫痪。

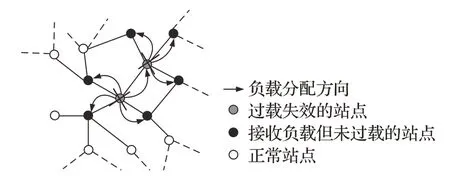
图1 级联失效过程示意图Fig.1 Schematic diagram of cascaded failure process

3.1 站点初始负载及最大容量

站点介数很大程度上能反映站点的负载情况，因此以站点的介数作为初始负载的量化指标，对于站点总数为N的网络有：

式中，Qi(0)为站点i的初始负载；B i为站点i的节点介数。

假设城市轨道交通网络站点都有承担负载的能力，依据Motter-Lai模型[14]，站点的最大容量与其初始负载呈正相关且与备用能力系数有关，节点最大容量如式（10）：

式中，Ci为站点v i最大容量；α为备用能力系数（α＞0），是衡量站点超过初始负载时的处理能力的指标。

3.2 负载重分配模型

URTN中站点故障时，若其负载超过站点的最大容量，则会进行负载重分配过程，假设网络中失效站点为vi，又站点容量和站点介数呈正相关，则故障站点vi分配到其任意邻接站点v j的负载量如下：

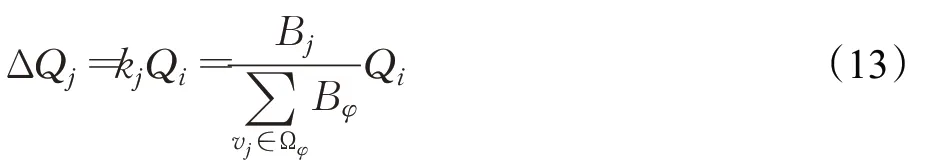
式中，ΔQ j为站点v j的负载增量；k j代表邻接站点的负载分配比例；B j为v j的介数；Ωφ是失效站点v i的邻接站点的集合。

3.3 级联失效传播过程

根据上述的负载重分配模型，城市轨道交通网络中，时间步长为t时故障站点v i的相邻站点v j实时负载量为上一时刻负载量与来自vi分流的负载量之和，即：

式中，Q j(t-1)为v j在t-1时刻的实时负载。

由于负载重分配过程导致失效站点的邻接站点负载发生改变，这时需要重新判断Q j(t)与C j之间的大小关系，若Q j(t)＞C j则该站点失效，进行新一轮的负载重分配过程，直至分配符合节点容量限制；若Q j(t)≤C j则不进行新一轮的负载重分配过程，即：

式中，“0”表示站点v j处于正常状态；“1”表示站点v j因负载过量处于失效状态。

3.4 级联失效算法及仿真流程

根据城市轨道交通网络级联失效模型，设计级联失效仿真算法如下：

步骤1建立城市轨道交通网络，将站点抽象为网络节点，将线路抽象成网络的边，形成无向无权网络。

步骤2初始化网络的备用能力系数α，计算节点介数B i，确定各节点初始负载Q i(0)及最大容量C i。

步骤3选取攻击策略（随机攻击或蓄意攻击），在网络中移除失效节点，更新网络状态。

步骤4对失效节点的负载进行重分配，根据负载重分配模型，将失效节点负载重分配到其相邻的节点，更新网络状态。

步骤5判断节点状态，判断失效节点的各邻接节点Ωφ的负载是否超过其节点容量，若没有，则级联失效过程结束，转步骤6，若超过，则进行新一轮的级联失效过程并在网络中移除失效节点，转步骤4。

步骤6级联失效过程结束，计算网络效率E以及最大连通子图比例S，评估网络的抗毁性。

具体仿真流程如图2所示。

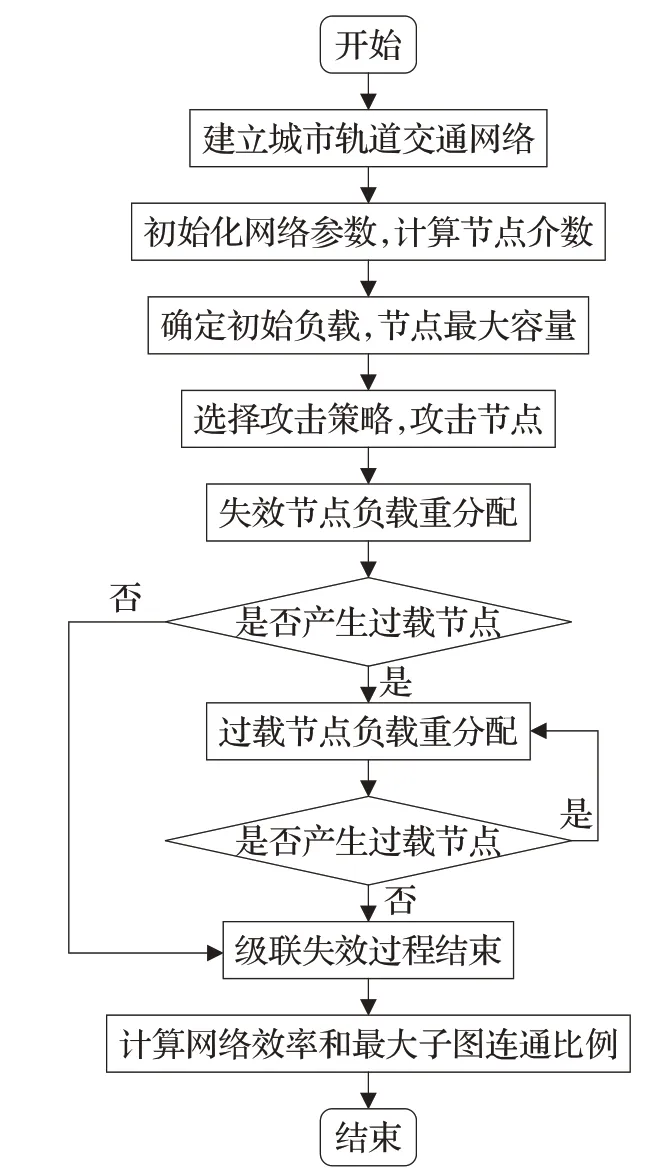
图2 级联失效仿真流程图Fig.2 Schematic diagram of cascaded failure simulation process

4 实例分析

上海是国内第三座开通地铁的城市，其轨道交通1号线于1993年5月28日正式运营，截止2020年12月31日，上海轨道交通运营线路共20条（含磁悬浮线），线路长度778.2 km，车站数432座（其中换乘站65座），运营里程和线网规模均为世界第一，利用Space-L法建立上海轨道交通网络拓扑模型如图3所示。

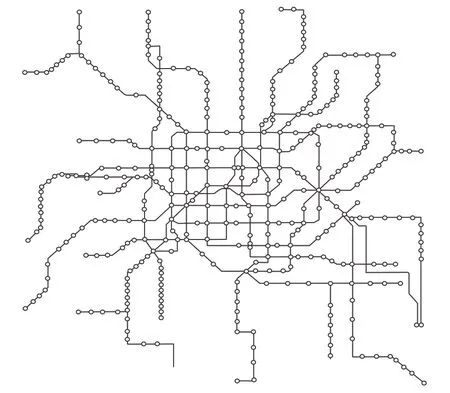
图3 上海轨道交通网络拓扑结构Fig.3 Topological structure of Shanghai rail transit network

上海城市轨道交通网络拓扑模型构建说明：

（1）数据选取截止日期为2020年12月31日的上海市轨道交通网络运营数据，共19条线路，345个站点（换乘站仅统计一次），不考虑规划及在建站点，对站点依次编号（1～345）。

（2）不考虑客流量、方向及其他客观因素，将城市轨道交通网络抽象为无向非加权网络。

（3）考虑到两座浦电路站不在一处，将其视为两个不同站点。

（4）统计数据时未将金山铁路线考虑在内。

4.1 上海轨道交通网络特性分析

利用python编程计算上海轨道交通网络特性指标，结果如表1所示，上海市轨道交通网络共有345个站点，394条边，网络的平均度为2.28，即网络中每个站点平均与2.28个站点连通；平均最短路径长度为16.06，即起始站点与目的站点之间平均需经16.06个站点才能实现连通，平均介数、平均聚集系数、网络全局效率以及连接度都偏低。

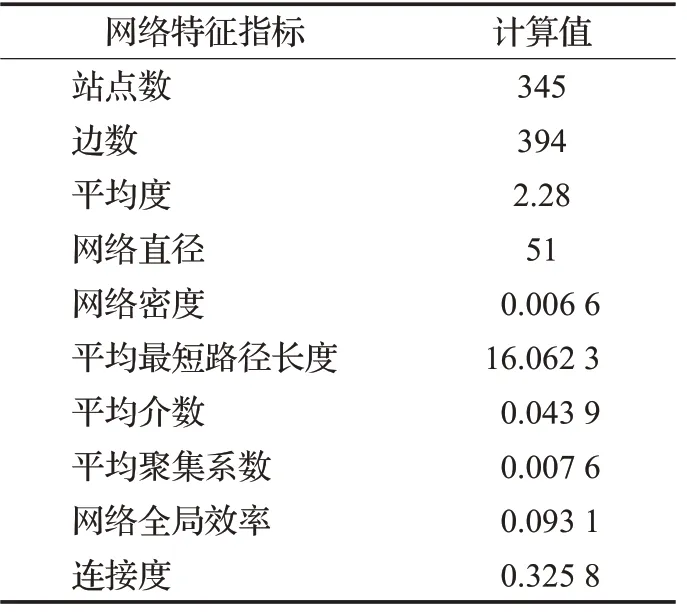
表1 上海轨道交通网络基本特征指标Table 1 Basic index of Shanghai rail transit network

如图4为上海轨道交通网络站点度分布及累计度分布，网络中有22个站点度值为1，这些是首末站，有267个站点度值为2，占网络总站点数的77.39%，为仅有一条线路通过的站点，度值为4点有42个，占比12.17%，为两条线路通行的换乘站，最大度值为8，站点为世纪大道站。

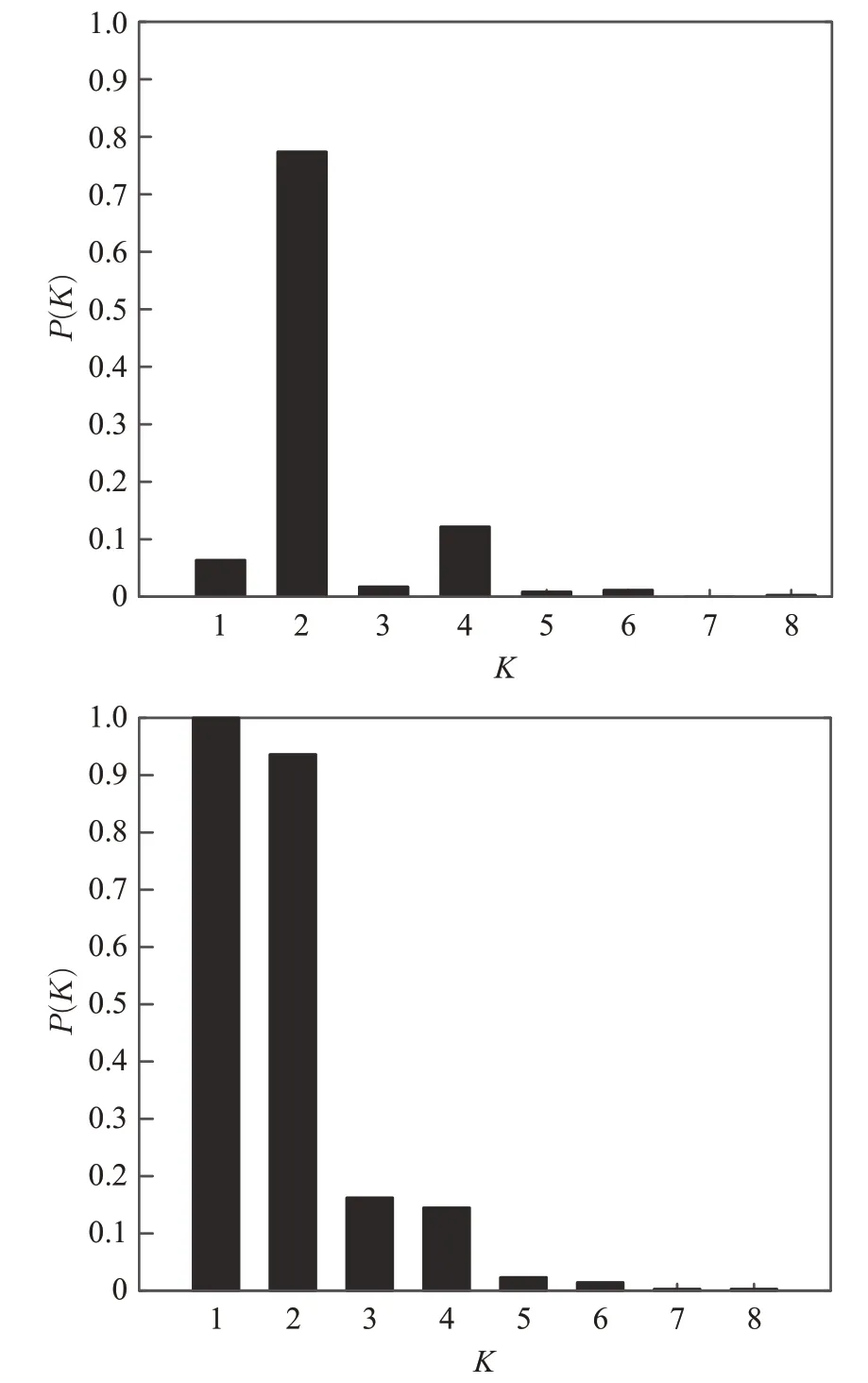
图4 站点度分布及累计度分布Fig.4 Distribution of degree and cumulative degree

对上海城市轨道交通网络站点累计度分布进行拟合，拟合函数及结果如图5所示在双对数坐标下，上海轨道交通网络的累计度分布概率服从幂律分布，拟合系数为R2=0.866 7，拟合效果良好，满足Barabási和Albert提出的网络中很少的节点具有较大的度，大部分节点具有较小的度，且网络站点累计度分布概率服从幂律分布的无标度网络的特性[15]。因此，上海轨道交通网络在L空间下符合无标度网络的特性。

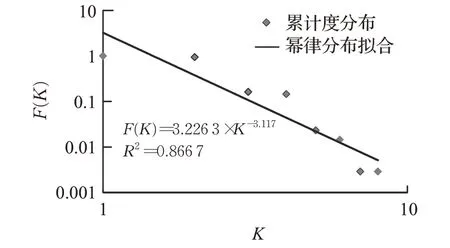
图5 上海轨道交通网络双对数坐标累积度分布拟合曲线Fig.5 Fitting curve of cumulative degree distribution of Shanghai rail transit network in log-log plot

进一步验证上海轨道交通网络是否具有小世界网络的特性，文献[16]提出小世界网络拥有如随机网络一样较小的平均最短路径以及和规则网络一样较大的聚类系数，且相比于随机网络具体满足以下两个条件[18]：

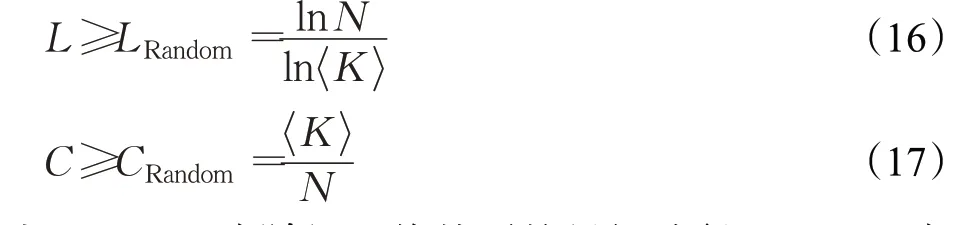
式中，LRandom为随机网络的平均最短路径，CRandom为随机网络的聚类系数。

根据式（14）和（15）计算与上海轨道交通网络同规模（相同的节点数、边数、平均度）的随机网络的特性指标，计算结果如表2所示。可以看出上海轨道交通网络的平均路径长度与网络聚集系数均大于同等规模的随机网络，因此上海轨道交通网络在L空间中满足小世界网络的网络特性。

表2 上海轨道交通网络和同规模随机网络拓扑特征参数Table 2 Topological characteristic parameters of Shanghai rail transit network and random network

表3中所示为上海轨道交通网络站点介数分布情况，可以看出网络中大部分站点介数很小，极个别站点介数较大，有约90%的站点介数值小于0.1，仅有5个站点介数值大于0.2，站点介数值具有明显幂律分布特点。其中有23个站点介数值为0，这些站点大多位于网络的边界位置，在选择最优路径时没有太大作用。

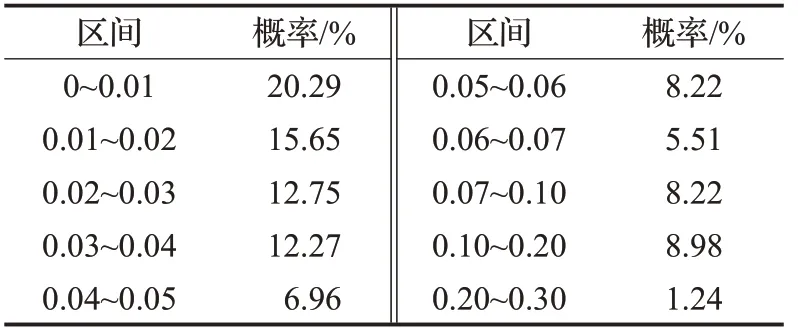
表3 上海轨道交通网络介数值分布Table 3 Distribution of betweenness values of Shanghai rail transit network

如图6为上海轨道交通网络站点介数与站点度值的关系，从图中可以看出度值小的站点对应的介数值在0.1内分布较为密集，度越大，则介数在较大的范围内变化，且分布较为分散，这说明度值大的站点通常也具有较大的介数值，对网络最优路径选择有重要影响。

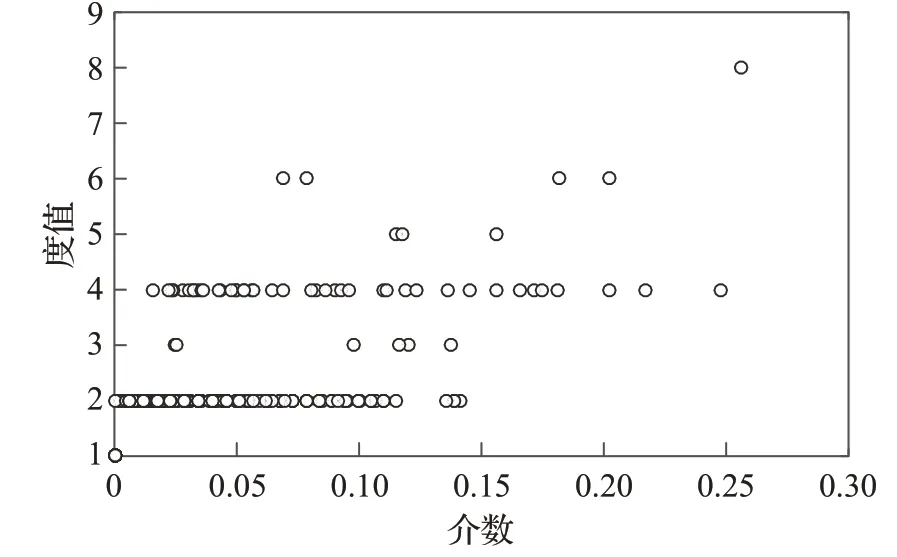
图6 上海轨道交通网络的度与介数关系图Fig.6 Relation diagram of Shanghai rail transit network degree and betweenness centrality

上海轨道交通网络直径为51，即任意两站点间最短路径最大值为51。如图7是网络最短路径概率分布及累计概率分布图，网络平均路径长度为16，任意两站点间最短路径长度小于等于16的占整体比例的56%；73%的站点间距离不超过20；乘客出行较为便捷，站点设置比较合理。

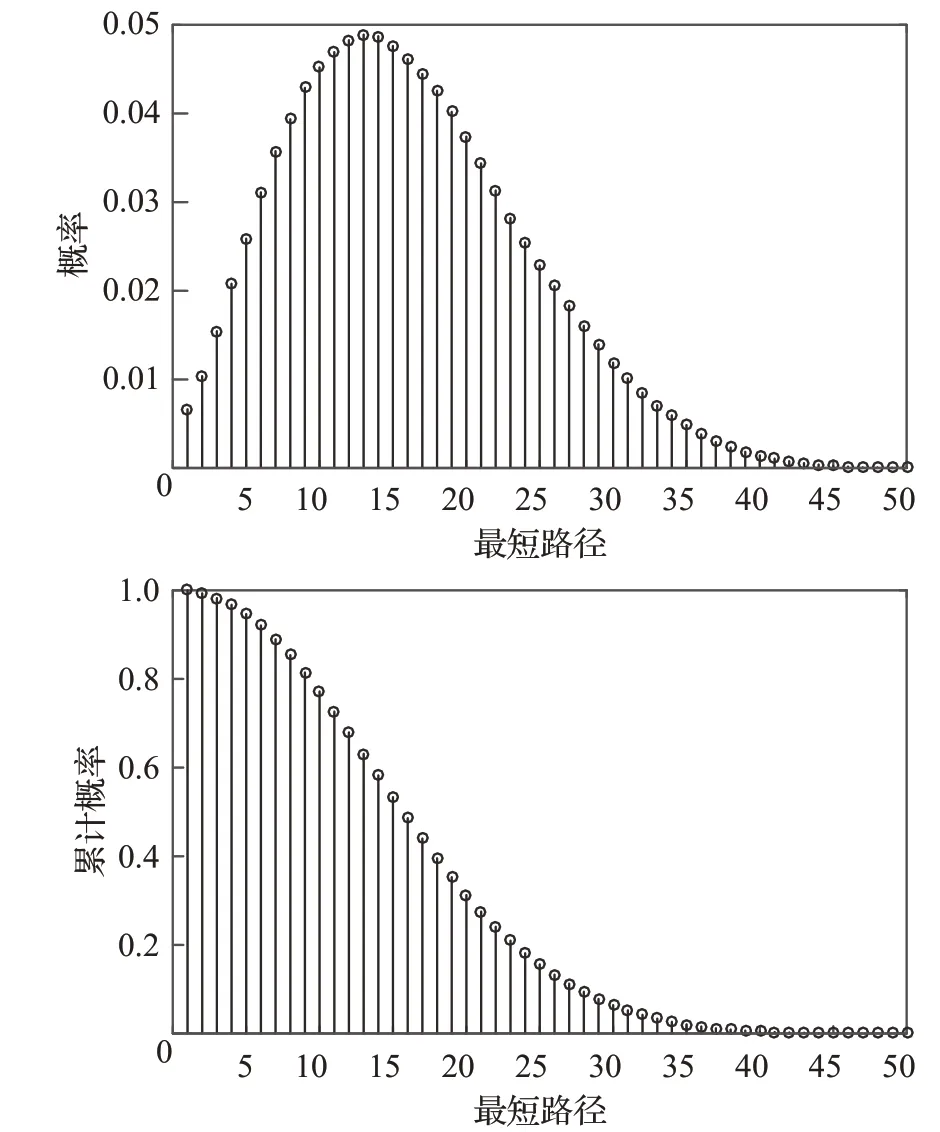
图7 最短路径概率分布及累计概率分布图Fig.7 Distribution diagram of shortest path probability and cumulative probability

表4为上海轨道交通网络聚类系数非0的12个站点，这些站点两两相连在网络中呈现三角形结构，如上海体育馆、徐家汇、宜山路，又如龙华中路、东安路、大木桥路。其余站点聚类系数均为0，站点间聚类系数低。这说明上海轨道交通网络容错性较差，一旦站点发生故障可替代的线路少，将会给网络整体运行带来较大影响。

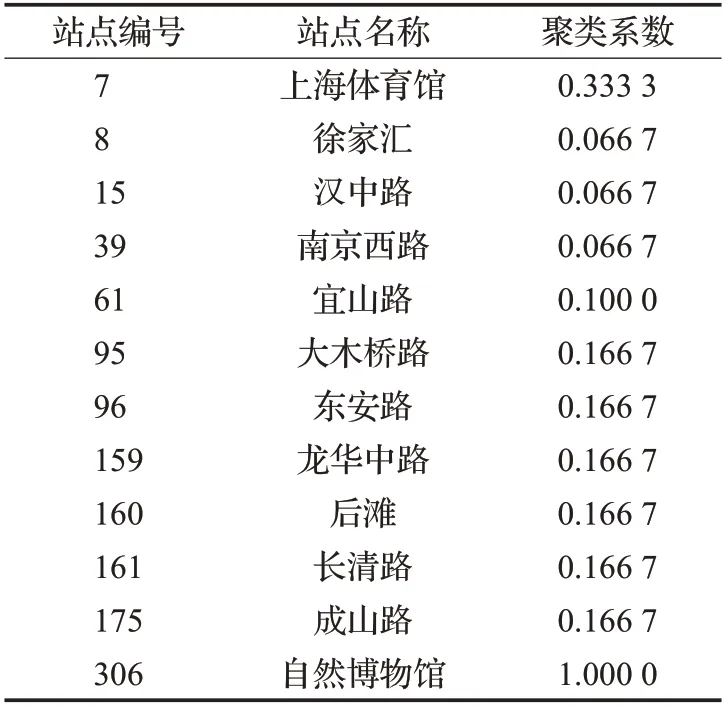
表4 站点的聚类系数Table 4 Clustering coefficient of stations

4.2 上海轨道交通网络重要站点

根据前文提出的站点重要度综合评价指标，不同权重系数组合下网络性能表现计算结果如表5所示：当λ=0.8，μ=0.2时，网络效率值为0.035 17，最大连通子图比例为0.620 3，网络性能变化率最大，因此，选用这组权重组合作为上海轨道交通网络站点重要性评价指标的权重系数。

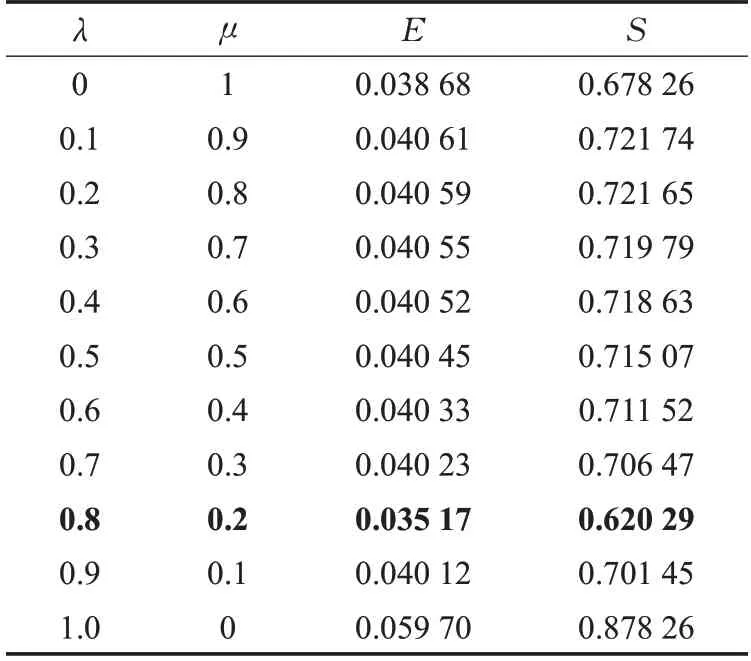
表5 不同λ、μ组合网络性能表现Table 5 Network performance as function of bothλandμ

根据综合评价指标确定上海轨道交通网络重要性排序前5%的站点如表6所示，这些站点在网络中发挥着重要作用，一旦故障可能会对轨道交通网络造成严重的破坏，导致整个网络的运行效率和连通度大幅降低。因此需要对这些站点加强防护，优化基础设施配置，降低故障发生率，以保证网络的正常运营。

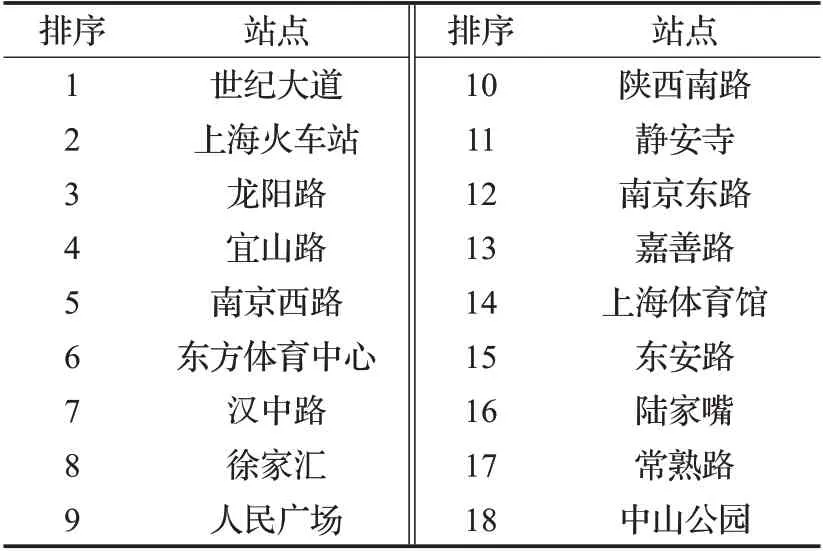
表6 上海轨道交通网络重要度排序前5%站点Table 6 Top 5%stations of Shanghai rail transit network in importance order

4.3 鲁棒性分析

城市轨道交通网络的鲁棒性是指在站点遭受突发事件时仍能保持网络正常有序运行的能力，网络级联失效鲁棒性是指站点遭受突发事件发生级联失效现象时仍能保持网络正常运行的能力。

4.3.1 鲁棒性评价指标

（1）网络效率E

URTN中站点(vi,v j)之间的效率指两站点之间距离d ij的倒数1/d ij，当站点之间的距离越短时，则站点的效率越高，可用于衡量城市轨道交通的运行效率，整个城市轨道交通网络的网络效率E定义为网络中站点之间所有距离的倒数平均值，计算公式如下：

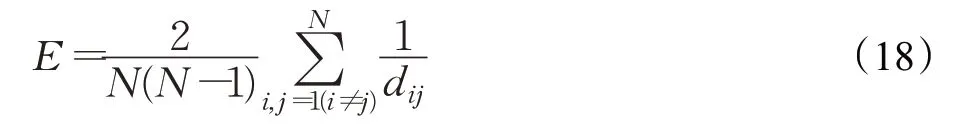
式中，N为网络站点总数，d ij为站点v i与v j之间的距离，若v i与v j之间不连通，则有d ij→+∞,1/d ij→0。

（2）最大连通子图比例S

当URTN受到攻击会被分为两个或多个子网络，且相互之间不连通，其中包含站点最多的子网络称为最大连通子图，用于度量网络的整体连通性。最大连通子图比例是指网络受到攻击之后最大连通子图包含站点总数与网络站点总数之比，计算公式如下：

式中，N′为最大连通子图所含节点数目，N为网络初始节点总数。

4.3.2 攻击策略

采用随机攻击及蓄意攻击两种攻击策略对城市轨道交通网络进行攻击，对比分析其在非级联及级联失效情况下的鲁棒性。随机攻击对应城市轨道交通日常运营中的自然灾害、信号故障、设备故障等随机故障，蓄意攻击则对应恐怖袭击、人为纵火等有强烈目的性的破坏行为，蓄意攻击主要针对网络中的重要站点。

随机攻击是利用python编程生成随机序列对已编号的网络站点进行移除。蓄意攻击又分为度值攻击、介数攻击及重要度攻击，分别按照节点度值、介数值和前文确定的节点重要度降序排序，然后在网络依次移除相关站点。其中，级联失效模型中备用能力系数α取值0.2。

4.3.3 仿真结果分析

如图8为上海轨道交通网络在非级联失效与级联失效情况下面对不同攻击策略时网络效率的变化情况。从中可以看出，非级联失效随机攻击下，网络效率下降缓慢，这说明小范围内随机故障对网络整体运行影响不大，但随着故障规模的扩大也会对网络造成较大影响，当移除节点数达到65个时，网络效率仅为初始效率的25.2%，而在级联失效随机攻击情况下，网络效率下降与非级联失效趋势相差不大，但当移除节点数达到42个时，网络效率发生突降，这可以解释为随机攻击移除了网络中的重要站点，从而引发多轮负载重新分配过程，造成多个站点失效，对网络效率产生较大影响，导致网络效率骤降。网络在面对蓄意攻击时，网络效率快速下降，在非级联情况下，当移除节点数为15个时，介数攻击和重要度攻击下的网络效率分别下降到初始效率的13.11%和5.64%，这说明攻击的这部分站点在网络中尤为关键，发挥着连通轨道交通网络的关键作用，且重要程度高的节点失效之后将会给整个网络带来更加严重的后果。在级联失效情况下，攻击重要度前5的站点造成网络效率下降初始网络效率的21.40%，攻击重要度前12的站点时导致网络效率下降至初始效率的1.79%，介数攻击和度值攻击同样对网络破坏极大，当攻击站点数达到13个时，网络效率下降至初始的3.18%和11%，网络均受到毁灭性打击，无法正常运行。

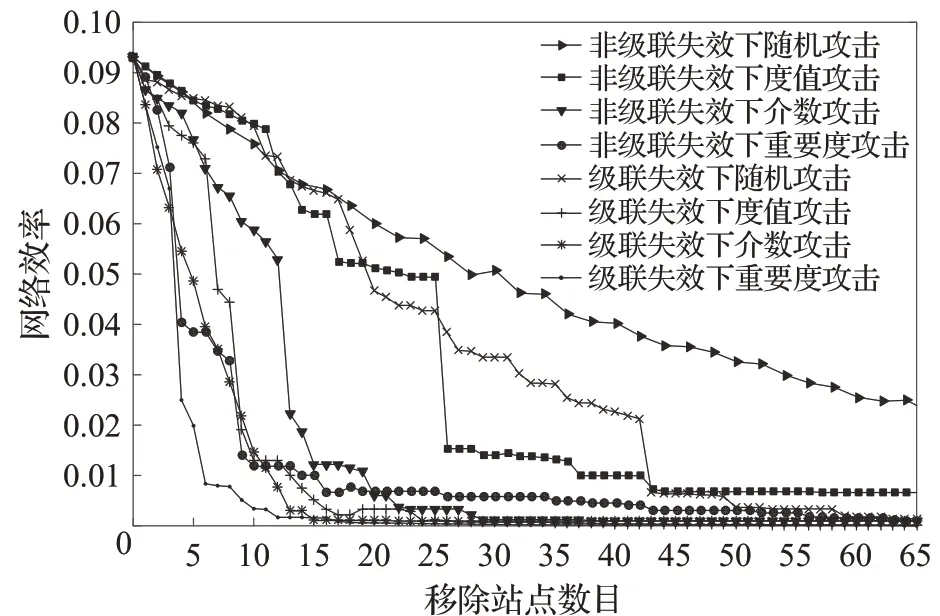
图8 不同攻击方式下的网络效率值Fig.8 Network efficiency values under different attack modes

上海轨道交通网络不同攻击策略下的最大连通子图比例变化情况如图9所示，在随机攻击策略下，最大连通子图下降趋势比较缓慢，但当移除站点数达到一定数量，一旦关键站点失效且存在级联失效现象，就会造成网络大部分剩余站点失效变成孤立站点，导致最大连通子图比例骤降。在度值攻击、介数攻击及重要度攻击三种蓄意攻击策略下，最大连通子图比例变化显著，在级联失效情况下，当移除站点数为12时，网络最大连通比例分别下降至26.95%、12.75%和9.28%，网络连通性受到极大地影响，非级联失效情况下，网络最大子图连通比例前期快速减小，之后变化较小且整体平稳下降。

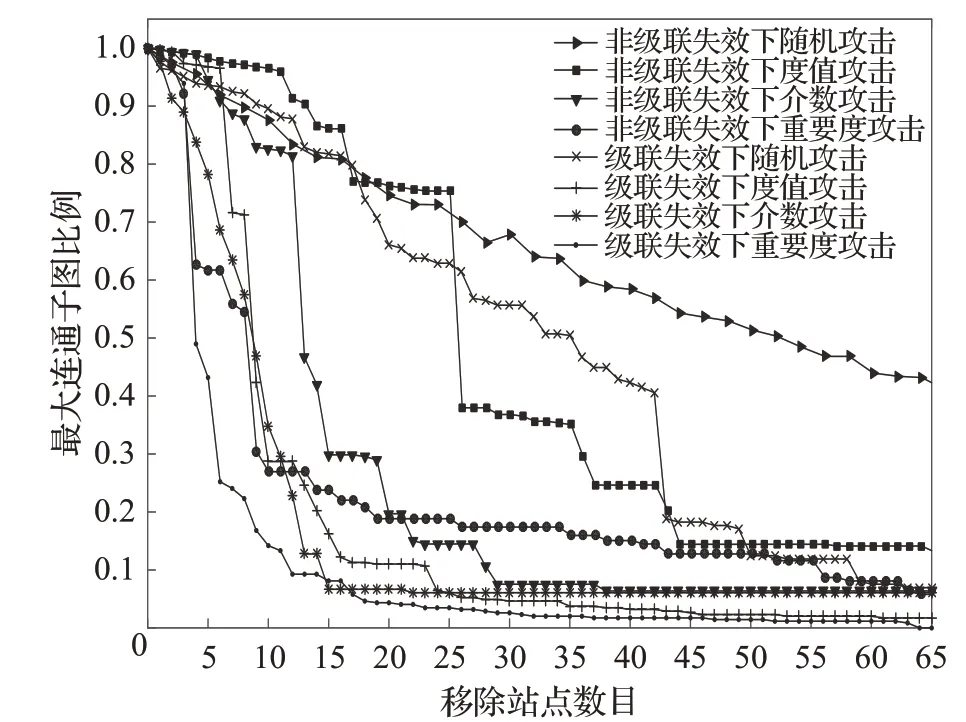
图9 不同攻击方式下的最大连通子图相对大小Fig.9 Relative size of largest connected subgraph ratio under different attack modes

此外，备用能力系数α对网络的级联失效鲁棒性也有一定的影响，如图10所示为α取不同值时移除站点数目对上海轨道交通网络最大连通子图比例影响情况，可以看出随着α的增大，网络最大连通子图比例下降趋势减缓，这是因为随着α的增大，车站最大容量随之增加，网络发生级联失效现象的概率就会变小，站点失效对网络造成的影响也就越小，网络的级联失效鲁棒性就会增强。因此，在改扩建城市轨道交通站点时，针对关键站点，应在满足日常客流量需求的基础上适当增加一定的容量，以降低站点级联失效的影响范围，增强URTN的抗毁性能，保障城市轨道交通的安全运营。

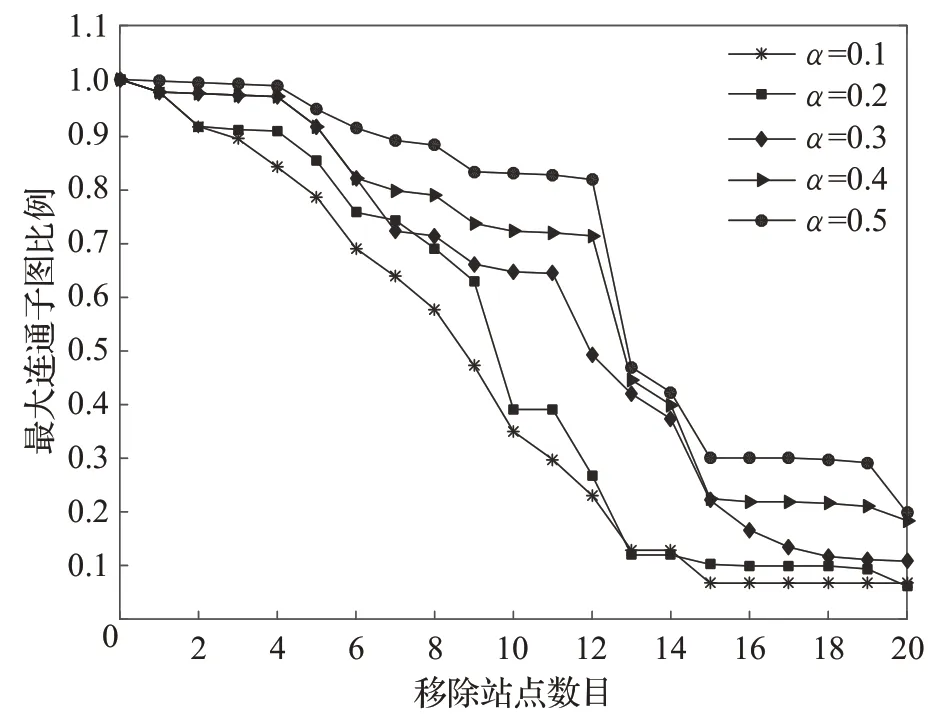
图10 不同备用能力系数下的网络效率比Fig.10 Network efficiency ratio under different reserve capacity coefficients

通过上述分析可知，上海轨道交通网络在随机攻击下表现出一定的鲁棒性，在蓄意攻击下具有较强的脆弱性，在考虑级联失效情况时，脆弱性更加明显，即上海轨道交通网络在面对设备故障、信号干扰、自然灾害等随机故障时基本可以维持运营，但在恐怖袭击等人为蓄意破坏下，网络会全面奔溃。因此一定要做好重要站点的安全防护，确保城市轨道交通的安全运营。

5 结束语

本文基于复杂网络理论，采用Space-L方法构建了城市轨道交通网络拓扑结构，结合度值中心性和介数中心性提出站点重要性综合评价指标，挖掘城市轨道交通网络的重要站点，建立了城市轨道交通网络级联失效模型。实证分析了上海轨道交通网络的网络复杂特性与级联失效鲁棒性，结果表明：（1）上海轨道交通网络平均最短路径较短，乘客出行较为便捷，但聚类系数偏低，网络容错性差，一旦站点发生故障可替代的线路少，将会给网络整体运行带来较大影响；（2）在L空间中，上海轨道交通网络站点累计度分布概率服从幂律分布，且满足小世界网络平均路径长度和聚集系数的要求，具有无标度网络和小世界网络的网络特性；（3）上海轨道交通网络在随机攻击下具有一定的鲁棒性，在蓄意攻击下表现出脆弱性，考虑级联失效情况时，脆弱性更加明显，因此要加强关键站点的日常维护和安全防护；（4）在对城市轨道交通站点进行改扩建时，针对关键站点，应在满足日常客流量需求的基础上适当增加一定的容量，增加车站备用能力，以保障突发事件下城市轨道交通的安全运营。研究仅从URTN物理层面分析网络拓扑特性和级联失效过程，未考虑乘客换乘、列车发车频次等情况，此外，研究将URTN建模为无权无向网络，未考虑客流加权情况，今后应结合上述情况进一步深入研究。