基于小样本学习和因果干预的ResNeXt对抗攻击

王志勇，邢 凯，邓洪武，李亚鸣，胡 璇

1.中国科学技术大学 网络空间安全学院，合肥 230026

2.中国科学技术大学 苏州研究院，江苏 苏州 215123

随着深度学习技术在自动驾驶[1]、自然语言处理、安防监控等[2-3]重要领域中的快速发展和应用，现有的深度学习模型逐步成为了高价值攻击目标并暴露了一些安全缺陷。研究者提出了多种攻击手段，通过对正常图片添加人类难以察觉的各种微小扰动，成功生成了使深度学习模型失效的对抗样本[4-5]。例如，Worzyk等人[6]使用对抗攻击算法生成的交通标志能诱导自动驾驶系统做出危险操作。

虽然目前的对抗攻击技术可以生成对现有深度学习模型具有威胁的对抗样本，但其需要依赖海量算力和海量数据的支持，在计算效率和攻击成功率提升方面仍存在较大挑战。首先，深度学习模型的海量参数以及庞大的样本解空间导致对抗攻击需要大量算力。对抗攻击技术需要基于被攻击深度学习模型的梯度反向生成图像扰动，计算过程需要使用海量算力搜索庞大的样本解空间，寻找最优扰动。此外，深度学习技术发展带来的一个影响就是深度学习模型的广度和深度被大大扩展，模型参数量巨大，例如常用的ResNet50参数量为25×106，而ResNet152参数量甚至高达60×106[7]，对算力要求较高。其次，基于海量算力搜索而非结构化分析的方法难以得到最优扰动，限制了对抗攻击的成功率。Goodfellow等人[8]的研究表明，对抗攻击方法生成扰动的方向取决于目标输出对输入图像的梯度，即扰动方向依赖于网络结构，海量算力依旧无法保证扰动方向的最优性，生成的扰动可能会给图像带来过大的变化，生成的图像在人类的视角下已经改变了类别，攻击失败。针对这些挑战，研究者们提出了各种解决方法，不断推动该领域的发展。

为了降低对抗攻击技术的算力要求，当前的研究通常将对抗攻击的优化问题简化，固定对抗攻击算法的搜索方向。例如，Goodfellow等人[8]提出了fast gradient sign method（FSGM），仅需沿着梯度方向对原始图像修改一次。更进一步，Kurakin等人[9]提出iterative gradient sign算法，沿着更优的梯度方向多次修改原始图像。另一个优化方向是使用生成对抗网络（GAN）。Xiao等人[10]第一个提出使用GAN生成对抗样本，并训练了一个生成器AdvGAN来学习对抗样本的分布。Jandial等人[11]提出AdvGAN++，使用GAN学习从图像中间层特征到对抗样本的过程，而不是学习从原始图像到对抗样本的过程。对于FSGM类方法，计算效率较高，但无法得到最优扰动，降低了攻击成功率，对于GAN类方法，当AdvGAN训练完成，输入原始图像即可直接输出对应的对抗扰动，但是GAN训练难度大。

为了提高对抗攻击的成功率，研究者们不断尝试根据深度学习模型的结构寻找更优的扰动方向或者使用Momentum技术优化计算过程。Szegedy等人[12]基于L2范数和交叉熵损失函数提出L-BFGS对抗攻击算法，使用该攻击算法能计算出一个扰动方向，并沿着该扰动方向生成对抗样本。Carlini等人[13]进一步总结对比前人的工作，基于最大化任意类别概率和真实类别概率之间差值的思想提出了C&W’s Attack算法，该算法可以计算出一个更优的扰动方向。此外，由于对抗攻击算法基于梯度求解最优扰动，Dong等人[14]提出使用Momentum技术优化梯度计算过程，增加扰动方向的稳定性。需要注意的是，深度学习模型使用卷积层提取图像特征，但是部分网络结构提取了噪音信息，攻击提取噪音信息的结构会对图像产生不必要的扰动，降低对抗攻击的成功率，所以对抗攻击技术应该避开噪音结构。

现有的方法大多基于海量算力来搜索合适的噪声扰动，对算力要求高且搜索效率难以保证，缺少一种结构化的识别深度学习模型弱点的方法。本文利用少量样本，基于因果干预手段分析了深度学习模型的结构弱点-时不变稳定结构，并基于Wasserstein距离来定位ResNeXt50/ResNeXt101的结构弱点，针对其弱点设计了一种对抗攻击算法，进一步验证了其结构性弱点的存在及其有效性，大大提高了对抗攻击计算效率和成功率。本文的贡献如下：

（1）提出深度学习模型的结构性弱点分析方法，仅需要少量数据即可定位深度学习模型结构的攻击弱点。

（2）提出一种基于L∞范数的结构化攻击方法，可以针对性高效生成对抗样本。

（3）提出一种针对深度学习模型中间层目标输出的通用扰动生成方法。

1 相关工作

1.1 Wasserstein距离

Wasserstein距离的起源是最优传输理论，描述的是将一个分布转化为另一个分布需要的最小代价，对于两个一维分布X、Y，其Wasserstein距离可表示为：

其中F X和FY分别表示X和Y的累积分布函数。

相对于常见度量方式，Wasserstein距离有着如下优势：

（1）能够度量离散分布和连续分布之间的距离。

（2）能够度量两个没有交集的分布之间的距离。

（3）考虑了分布的几何特性，不仅可以计算两个分布之间的距离，还能从几何角度解释两个分布之间不同之处。

因为Wasserstein距离的优秀性质，很多研究使用Wasserstein距离优化深度学习模型。例如Arjovsky等人[15]提出一种基于Wasserstein距离的生成对抗网络WGAN，提高深度学习模型训练的稳定性，克服模式崩溃等问题，Gulrajani等人[16]提出了一种方法代替WGAN中的削减权重方法，进一步提高了WGAN的训练稳定性，Frogner等人[17]基于Wasserstein距离设计了一种多标签学习的损失函数。

1.2 对抗攻击

Szegedy等人[12]第一个提出攻击深度学习模型的对抗攻击算法，通过对正常图像添加微小扰动，制作了一个对抗样本，这个样本能够使当时最优秀的深度学习模型失效。文章提出一种对抗攻击算法L-BFGS，该方法的目标函数是：

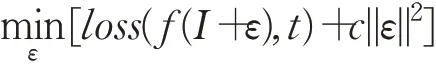
其中I表示原始图片，f表示深度学习模型，t表示错误标签，c是超参数（最优值可通过搜索得到），该目标函数可以找到一个最小的噪音ε，添加到原始图片上，得到一张被误分类为t的对抗样本。发现对抗样本现象后，Goodfellow等人[8]证明深度学习模型的高维线性是对抗样本具有对抗性的原因。当模型具有高维线性时，沿梯度方向的扰动越大，样本对抗性越强。文章据此提出了一种对抗攻击算法fast gradient sign method（FGSM）：

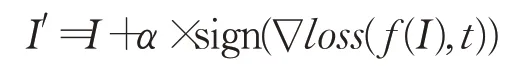
其中I′表示对抗样本，I表示原始样本。该方法根据各像素点与目标标签的梯度关系，逐像素修改原始图像，使得修改后的图像远离类别t。后续在FGSM基础上，Kurakin等人[9]提出iterative gradient sign算法，采用迭代的方式沿着目标方向多次修改原始图像，得到更优秀的对抗样本。不同于前述方法使用L∞范数，Papernot等人[18]提出一种基于L0范数的对抗攻击方法：jacobianbased saliency map attack，该方法计算一个显著性map，根据这个map定位对目标类别影响最大的像素点，修改这部分像素点，直至图像被误分类。Croce等人[19]同时使用L0和L∞范数，进一步提高了对抗攻击的成功率。基于Goodfellow等人[8]对深度学习模型的高维线性解释，Moosavi-Dezfooli等人[20]提出DeepFool方法，该方法将深度学习模型视为线性函数，决策边界视为一个超平面，使用迭代的方式修改原始图像，使得修改后的图像越过决策边界，得到对抗样本。Carlini等人[13]总结了前人方法，提出了C&W’s Attack方法，该方法将图像像素值映射到无穷区间，并使用了一个更高效的目标函数。不同于前述使用L范数定义图像失真度，Laidlaw等人[21]提出使用颜色变化定义图像失真度，并使用特殊目标函数将图像中所有红色像素更改为浅红色，得到对抗样本。Sharif等人[22]提出一种算法生成眼镜状扰动，并添加到人脸图片上，得到一张使得深度学习模型失效的对抗样本。Komkov等人[23]提出AdvHat算法，可以生成一张可打印图片，将图片贴在额头即可使最先进的Face ID模型失效。

不同于前述方法仅仅基于深度学习模型输出，Sabour等人[24]提出feature adversary方法，该方法的思想是将被攻击图像的特征层输出向着目标类别移动，并证明该方法得到的对抗样本在特征角度上更加契合总体样本分布。

最近的研究还将GAN引入对抗攻击领域，提出AdvGAN，使用GAN网络生成对抗样本。AdvGAN架构包括三个部分：生成器G、判别器D、被攻击网络f，生成器G用于根据输入图像生成对抗样本，判别器D用于引导G生成与原始图像难以区分的对抗样本。传统方式使用L范数度量限制图像与原始图像之间的失真度，而AdvGAN方法使用判别网络限制生成图像与原始图像之间的失真度，可以有效减少对原始图像的修改，提高攻击成功率。此外AdvGan中的对抗样本生成网络G一旦训练完成，可以在不接触被攻击模型的情况下根据输入图像直接输出对抗样本。进一步，Zhao等人[25]提出Natural GAN，由原始图像得到特征向量，对特征向量进行扰动，通过扰动后的特征重构出更加自然的对抗样本。

2 深度学习模型时不变稳定结构弱点分析方法

2.1 基于数据增强技术的序列数据调制生成

因果关系可以更好的理解深度学习模型的机制[26]，而深度学习模型的时不变稳定结构可以识别出输入输出之间的因果关系，因此可以通过因果分析定位时不变稳定结构。Peters等人[27]的研究表明，相对于非时序数据，通过时序数据分析因果关系的时候，需要的假设条件较少，效果较好。例如格兰杰因果关系检验[28-29]，该方法检验一组时序数据是否可用于预测另一组时序数据。

为了便于进行因果分析，需要将图像数据这样的非序列数据转换为序列数据进行因果分析，定位时不变稳定结构。本文使用数据增强技术，经过调制干预，将非时序图像数据生成为序列数据。

数据增强技术[30-31]常用来扩展数据集，帮助深度学习模型学习到更多的信息，减少过拟合，提高深度学习模型泛化性能，其原理是，在不改变物种属性情况下为图像添加噪音，例如高斯模糊、图像缩放、图像旋转、物体位移，这些数据增强方式不会改变图像类别信息，仅会带来分辨率、尺度、视角、位置方面的图像噪音。本文定义了一个调制曲线，通过从调制曲线上获得的参数，将一张图片增强为多张连续变化的图片，获得序列数据。

本文序列数据调制过程描述为：

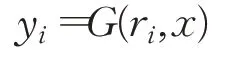
Subject that：

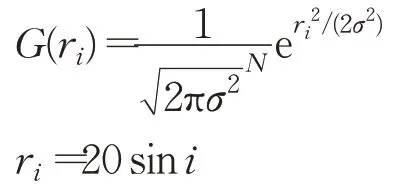
其中yi表示序列中第i个数据，G表示增强函数（此处以高斯模糊为例），r i表示从调制曲线r上选取的第i个参数，x表示原始图像，使用第i个参数将原始图像x增强为第i个数据，共100次，得到长度为100的序列图像数据。

本文选择的数据增强技术包括高斯模糊、图像缩放、物体位移。

2.2 时不变稳定结构

本文将调制序列数据类比于时间序列数据，其时不变稳定性即为深度学习模型在处理经调制干预后的序列数据时，能提取与输入序列有对应调制关系的信号，不受数据增强过程中人为添加的噪声影响。

Pearl等人[32]的研究认为，学习因果关系的人工智能需要具备三种不同层级的认知能力：观察能力、行动能力、想象能力。观察能力是指通过学习识别数据之间关联性的能力，行动能力是指能通过干预实验学习对数据干预后的结果，并且能根据学到的信息实现期望的结果，想象能力是指反事实推理能力，能够推测产生某种结果的原因。文献[32]认为目前的深度学习模型具备观察能力，部分网络结构具备行动能力，因此本文结合文献[32]的介绍，给出深度学习模型的时不变稳定性定义。首先，对图片使用数据增强技术后，产生的输入图像序列和神经元输出序列之间存在有对应调制关系的因果性，表现为神经元输出序列和调制曲线之间存在一致的变化趋势，这个一致性可以使用格兰杰因果关系检验判断。其次，对同类别不同图像使用数据增强技术后，神经元处的输出序列之间理应存在明显的相似性，因为相同类别的图像经过理想模型处理后会表达出相同的类别特征，且相同的类别特征具有一致的变化规律，表现为同类图像的输出序列之间存在相似性。再次，对不同类别图像使用数据增强技术后，神经元处的输出序列之间理应存在明确的差异性，因为不同类别的图像经过理想模型处理后应该表达出不同的类别特征，不同的类别特征具有不一致的变化规律，表现为不同类图像的输出序列之间有显著差异。最后，对同类图片使用数据增强技术后，神经元处的输出序列具有稳定性，因为数据增强技术不会改变图像的类别特征信息，增强后的图片具有和原图片一致的类别特征，表现为输出序列的方差较小。

基于上述分析，给出时不变稳定性形式化定义。

首先定义调制参数序列：

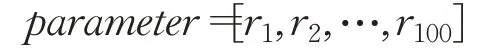
使用2.1节序列数据生成方式得到图像数据序列：

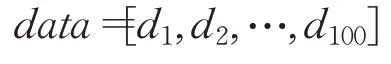
在神经元处得到各个图像数据的特征值序列：

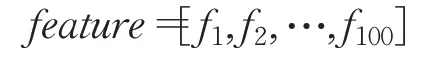
则parameter与feature两序列间存在因果性的结构即为时不变稳定结构：

2.3 基于Wasserstein距离的时不变稳定结构定位方法

根据前文时不变稳定结构性质介绍，本节通过调制干预后的序列数据来定位时不变稳定结构。Pearl等人[32]认为，通过干预可以控制混杂因子，进一步识别出因果关系，时不变稳定结构定位过程与该思想一致，即当固定其他变量，仅对输入数据进行干预，则时不变稳定结构的输出对干预有匹配的响应[33]。

深度学习模型的时不变稳定结构可以识别输入输出间因果关系，能克服数据增强带来的噪音，从输入图像中提取有效信息作为输出。对于图像序列，时不变稳定结构的输出序列与输入图像序列之间具有一致性，同时因为输入图像序列均为同一图像的调制结果，分布间距离理应较小，因此时不变稳定结构的输出序列分布间距离也应该较小。在考虑到Wasserstein距离的对称性以及几何特性，本文选择Wasserstein距离来度量分布间距离。考虑到本文的输入序列数据和深度学习模型输出之间的关系[29]，本文使用格兰杰因果关系检验来识别其时不变稳定结构。

对于同一张或同一类数据，本文使用数据增强技术调制，本文设计了图1的增强数据矩阵，增强过程可描述为，对一组同类图像使用一致的数据增强技术，增强多步。每个数据序列在时不变稳定性神经元处输出分布都具有相似性，此时使用Wasserstein距离度量相邻分布之间的距离，得到一阶差分序列，将该序列定义为2.2节中的feature序列，采用格兰杰因果关系检验来逐个判定高层神经元及其对应子结构的稳定性：

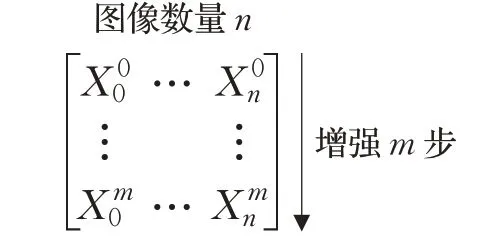
图1 序列增强数据示意图Fig.1 Schematic diagram of time series enhanced data

3 针对卷积神经网络结构性弱点的对抗样本生成方法

卷积神经网络通过卷积结构从图像中提取信息，并通过进一步的卷积操作将局部特征信息融合为高维抽象特征，提高神经元视野范围。不同部分和层次的网络结构能够提取不同的信息。

考虑到时不变稳定结构能够识别原始图像和添加噪声后的调制图像间的稳定调制关系，即能排除一般噪声干扰，提取有效信息。根据反事实推理[32]，攻击时不变稳定结构自然会影响深度学习模型的有效信息提取，因此时不变稳定结构是卷积神经网络的攻击弱点之一。

基于前述分析，本文使用时不变稳定结构优化GAN及传统对抗攻击技术。目前主流方法的目标是降低深度学习模型分类层正确类别对应的输出值，而本文方法的目标是降低时不变稳定结构的输出有效性，使得时不变稳定结构不再能够从输入中排除噪声干扰，也即不能得到具有因果性的输出。

此外，Szegedy等人[12]认为卷积神经网络通过卷积层的特征空间保存高级语义信息，而非使用单个神经元保存高级语义信息，所以攻击卷积神经网络时应该攻击卷积层特征空间，因此对抗攻击算法应将整个卷积层作为攻击目标，基于卷积层空间，使用海量算力搜索合适的噪声扰动。因此，本文的攻击方法也应该针对特征空间而非单个时不变稳定结构。

由此，本文考虑由时不变稳定结构以及噪音结构的输出组成的特征空间，通过第2章介绍的定位方法可以定位出全部时不变稳定结构，而由这些时不变稳定结构输出组成的卷积层特征子空间可以排除噪音干扰，稳定地提取出有效信息。因此本文所设计的攻击方法针对时不变稳定特征子空间进行攻击，首先可以更高效地在特征空间中识别出能影响这些子结构的噪声扰动方向。其次可以降低算力要求，因为算法的搜索域从原始特征空间缩小为其子空间，计算规模下降了多个数量级，仅需较少的算力即可从特征子空间中搜索出最优扰动，使得对抗样本的生成效率大大提高。

需要注意的是，不同类别具有不同的时不变稳定结构集合，但是这些结构从因果性角度具有相似的意义，因此针对时不变稳定结构的对抗攻击方法可以适用于任何类别。

根据上述分析，本文进一步提出一种针对深度学习模型时不变稳定结构的多类别通用扰动生成方法，将时不变稳定结构组成的特征子空间作为攻击目标，通过计算为图像添加对抗性扰动，降低该特征子空间输出的有效信号值，即可促使深度学习模型输出错误类别，进而实现对抗攻击。

具体地，在与原始图像各部分最大像素值差小于σ的有限搜索空间中找到噪声分布，该分布对应的图片能使特征子空间的平均输出值最小，该图片就是对抗样本。基于该目标，本文提出一种基于L∞范数的对抗样本生成方法，采用的目标函数如下：

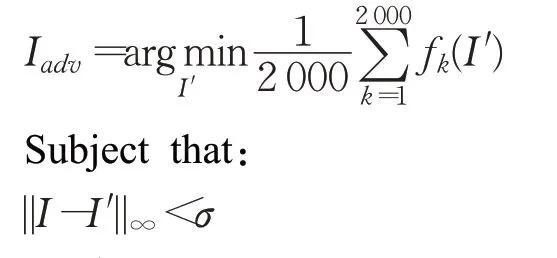
其中f k表示被攻击深度学习模型中的第k个时不变稳定结构的输出，I′表示对抗样本，I表示原始样本，σ表示对抗样本与原始样本最大像素值差，可自选值（本文中σ=20）。

基于Goodfellow等人[8]的启发，本文采用迭代的方式实现生成过程，可以进一步降低对抗攻击的算力要求：

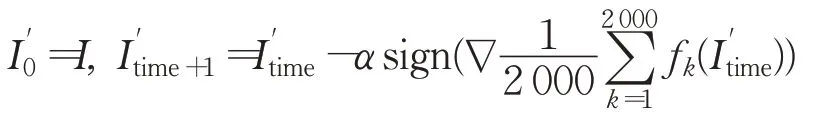
其中α表示步长，σα表示最长迭代步数，迭代过程中通过时不变稳定结构组成的特征子空间计算最优搜索方向，沿该方向搜索最优扰动。

整体流程图见图2，首先选定攻击类别，使用基于Wasserstein距离的方法定位时不变稳定结构，并组建卷积层特征子空间，作为攻击目标。然后选定原始照片，基于本节的攻击方法，迭代求解能最大化降低目标特征子空间平均输出的图像扰动，将该扰动添加到原始图像上，直到图像被误分类（攻击成功）或者达到失真点（攻击失败）。

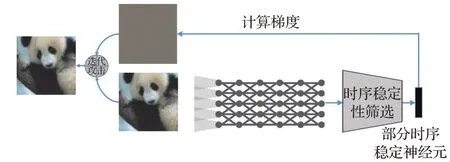
图2 攻击架构Fig.2 Attack architecture

最后，本文定义的判断时不变稳定结构的方法是基于该结构能提取高级抽象特征，所以需要在表达能力比较强的特征层上进行计算。Alexander等人[34]评估了常见深度学习模型各层输出特征的表达能力，实验发现ResNeXt的特征表达能力逐层提高，因为ResNeXt带有残差结构，能够保持表达能力。因此，本文选择最后一层卷积层作为目标层。

4 理论分析

Madry等人[35-36]认为微调图像，使图像区别于训练集数据分布，可以生成对抗样本，而区别于训练集的数据（out-of-distribution samples）可以使用基于能量得分的方法区分[37-39]。本文提出的方法可以从能量分析的角度出发，通过给图像添加人类难以察觉的微小扰动，降低卷积层特征子空间的输出值，降低图像能量得分，将训练集数据逐渐修改为out-of-distribution数据，直至生成对抗样本或者失败。

首先从能量角度给出图像x被分为各个类别的概率：

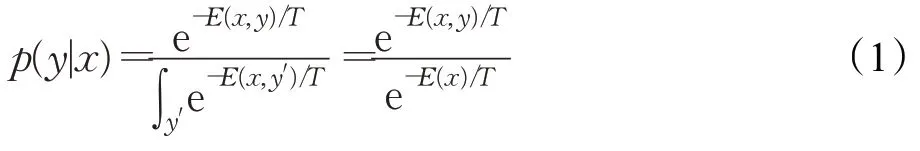
其中E(x,y)是能量函数，表示图像x和类别y的匹配度，能量越低，表示匹配度越高。

数据x的亥姆霍兹自由能为：

对于K分类深度学习模型来说，其分类层有K个输出值，对应K个类别，则图像x被分为各个类别的概率：

其中f i(x)表示将图像x输入神经网络后得到的第i个输出。

联立等式（1）和等式（3），可得：

联立等式（2）和等式（4），可得：

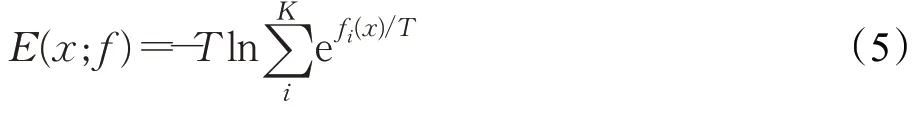
为了判别图像x是否为out-of-distribution数据，可以使用x的概率密度函数，图像出现的概率低就表示图像属于out-of-distribution数据，由前述定义给出图像x出现概率：

两边取ln，可得：

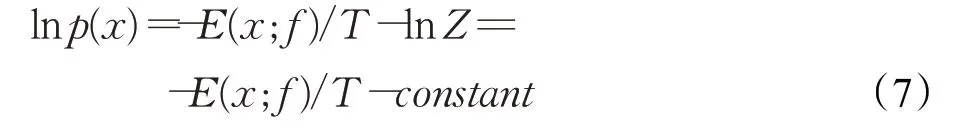
本文将-E(x;f)定义为能量得分，通过等式（7）可以看出-E(x;f)和lnp(x)呈线性关系，能量得分越低，图像出现概率越低，即图像属于out-of-distribution数据。

5 实验

5.1 实验设置

本文选用ImageNet LSVRC-2012数据集，被攻击的深度学习模型包括ResNeXt50以及ResNeXt101，均为PyTorch预训练模型。本文采用攻击成功率，攻击计算时间以及对抗样本L∞失真度作为评价指标，和C&W’s Attack以及Feature Adversary方法进行对比，并且基于召回率和能量得分评价攻击过程。

5.2 卷积结构神经网络时不变稳定性分析

使用第2章时不变稳定结构定位方法，分别计算ResNeXt50以及ResNeXt101各神经元输出序列的方差，如图3和图4所示。

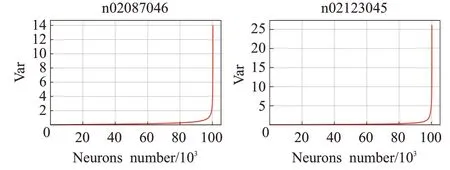
图3 ResNeXt50神经元输出序列的方差Fig.3 Variance of ResNeXt50 neuron output sequence

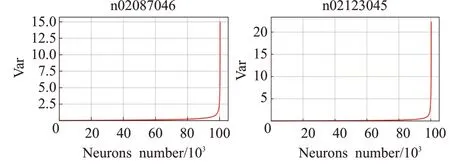
图4 ResNeXt101神经元输出序列的方差Fig.4 Variance of ResNeXt101 neuron output sequence

图中横坐标表示了神经元编号，纵坐标表示每个神经元处的方差，为了便于查看，本文按照方差从小到大的顺序对神经元进行编号，得到图3和图4。按照时不变稳定结构定义，方差较小的神经元具备时不变稳定性。从图中可以看出ResNeXt系列具有相似的性质，有70%的神经元方差接近0（时不变稳定结构），这一现象出现在各种类别中，本文展示了两个类别结果，证明了时不变稳定结构的广泛存在性。

5.3 基于召回率的攻击效果分析

为了验证时不变稳定结构的关键性和脆弱性，本节设计了以召回率作为指标的评价实验。将ResNeXt50/ResNeXt101全部神经元按照方差从小到大排序，选择方差最小的1/10神经元为一组，该组为时不变稳定结构，同时选择方差最大的1/10神经元为另一组，该组为非时不变稳定结构。对两组神经元做相同的干扰（每个神经元乘以一个倍数），查看深度学习模型召回率变化，得到图5和图6。

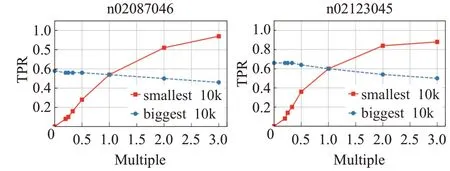
图5 ResNeXt50不同结构受干扰后召回率变化Fig.5 Recall change of ResNeXt50after different structures disturbed

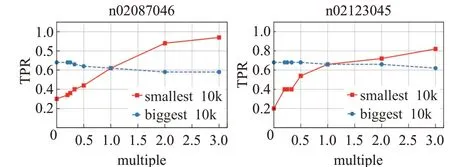
图6 ResNeXt101不同结构受干扰后召回率变化Fig.6 Recall Change of ResNeXt101 after different structures disturbed

图中横坐标表示干扰倍数，纵坐标是召回率。图中红色实线表示方差最小的1/10神经元，蓝色虚线表示方差最大的1/10神经元，两曲线交汇处是深度学习模型的原始召回率。从图中可以得出：

（1）降低时不变稳定结构的输出值（倍数小于1），ResNeXt50召回率快速下降至0，ResNeXt101召回率快速下降至0.2，而降低非时不变稳定结构的输出值后，ResNeXt50/ResNeXt101召回率变化都很小，证明了时不变稳定结构的关键性，时不变稳定结构的输出信号保证了深度学习模型的分类准确性。

（2）观察红蓝两曲线的斜率，可以看出红色曲线（时不变稳定结构）斜率远大于蓝色曲线，说明时不变稳定结构更易收到干扰，证明了时不变稳定结构的脆弱性。

5.4 基于能量得分的攻击过程分析

能量得分越低，图像出现概率越低，即图像区别于训练集数据。为了验证本文的方法可通过微调降低图像的能量得分，如图7展示了本方法迭代过程中图像的能量得分变化过程。

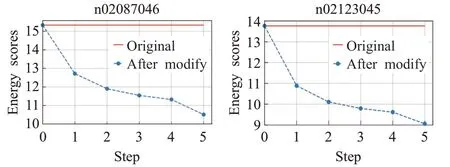
图7 生成对抗样本过程中能量得分变化Fig.7 Energy score changes during process of generating adversarial examples

图中红色直线表示原始图像的能量得分，蓝色虚线表示算法迭代过程中能量得分变化过程，从图中可以看出本算法能有效通过微调图像降低能量得分，使图像区别于训练集数据，最终得到对抗样本，使深度学习模型失效。

5.5 卷积结构神经网络攻击效果分析

首先展示部分攻击效果图，图8中展示了三张对抗样本：第一张Chihuahua图片添加干扰后得到一张被误分类为French bulldog的图片；第二张stingray添加干扰后得到一张被误分类为numbfish的图片；第三张terrapin添加干扰后得到一张被误分类为mud turtle的图片，对原始图像的修改均较小。

图8 对抗样本展示Fig.8 Adversarial sample display

然后分析本方法的计算效率。以ResNeXt50为例，对抗攻击的计算过程需要根据深度学习模型输出对输入的梯度确定搜索方向，沿着该方向计算扰动，并判断该扰动能否生成对抗样本。该过程需要迭代多次直到攻击成功或者失败。根据链式求导法则：

（1）之前方法。基于ResNeXt50分类层，计算梯度过程的计算量为1×2 048×2 048×7×7×N，N表示卷积层计算量，此外，由于之前的方法难以得到最优扰动，需要较多次迭代才能攻击成功。

（2）本文方法。基于ResNeXt50最后一层卷积层的2 000个神经元，因此计算梯度的计算量为2 000×N。且本文的攻击方法能得到更优扰动，需要较少次数的迭代即可完成对抗攻击。综上，本方法计算量远小于之前方法。

最后，本文选择了1 000张图片作为被攻击对象，对比了之前的对抗样本生成方法和本文方法的平均效果，指标包括对抗样本L∞失真度（对抗样本和原始样本的L∞距离），攻击成功率（本文设定σ＞20为攻击失败）以及平均攻击时间（不包含攻击失败样本），如表1所示。

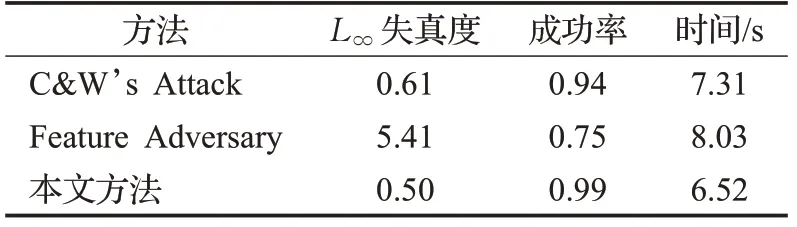
表1 传统方法与本文提出的方法对比Table 1 Comparison of traditional methods and proposed method in this paper

从实验结果可以看出，本文的方法在三项指标上均优于之前的对抗攻击方法。

6 结论

本文介绍了一种深度学习模型的时不变稳定结构，并提出了一种基于Wasserstein距离的定位方法，理论分析和实验表明时不变稳定结构是一种攻击弱点，最后针对该弱点提出了一种计算效率和成功率更高的对抗样本生成方法。本方法中使用的时不变稳定结构以及针对深度学习模型的结构弱点的思想，给后续对抗攻击方法研究提供了很好的方向。后续计划将基于深度学习模型的时不变稳定结构提高深度学习模型的泛化能力。