改进深度Q网络的无人车换道决策算法研究

张鑫辰，张 军，刘元盛，路 铭，谢龙洋

1.北京联合大学 北京市信息服务工程重点实验室，北京 100101

2.北京联合大学 机器人学院，北京 100101

3.北京联合大学 应用科技学院，北京 100101

无人驾驶技术可以使人们的出行更加方便、安全，同时也可以减少因人为因素导致的交通事故。而无人车换道决策问题是无人驾驶技术中的重要问题之一[1]，因此，如何在保证安全的前提下使无人车更有效率的行驶成为了研究者聚焦的重点[2]。目前，无人车换道决策算法主要分为两部分：基于规则的算法和基于机器学习的算法。基于规则的换道决策算法模型主要有间隙接受模型[3]、势场模型[4-5]、模糊逻辑模型[6]等，这些算法较基于机器学习的算法相比，泛化能力较弱，且往往得到二元的换道决策结果（换道、不换道），无法处理较为复杂和随机的动态道路场景中的问题。

针对基于规则换道决策算法存在的不足，基于机器学习的算法被逐渐应用于无人车换道决策的研究中。文献[7-8]使用支持向量机将数据集中无人车和无人车周围的环境车的车辆参数作为模型输入，最终对无人车的换道行为决策结果进行分类，这种方法虽然可以解决在高维的数据下的输入问题，但是由于数据量较大，算法的时间复杂度较高，导致效率较低。文献[9]使用随机森林和决策树对数据集进行分析，并分别输出了直行和换道的决策结果，然而这种方法需要收集车辆驾驶员的标签数据，这种标签数据的采集十分困难并且数据中的噪声会直接影响分类结果的准确性。当使用以上监督学习算法来解决无人车换道决策问题时，往往需要大规模数据集作为算法输入，导致算法训练时间较长，同时在训练时将数据集的标签数据当作“真值”，使得算法缺乏探索能力。文献[10]使用进化策略（evolution strategy，ES）对无人车换道决策算法进行研究，提出了基于ES的神经网络算法，使用并输出了保持原道，左换道，右换道三种结果。此方法虽然解决了梯度下降法易使模型收敛到局部最优的问题，但是优化速度较慢，计算成本较高。上述算法与基于强化学习的换道决策方法相比，往往需要大量的数据集作为输入用于模型训练，同时数据集中的噪声会直接影响模型训练的准确性，最终影响模型的测试结果。针对上述问题，研究者提出基于强化学习的无人车换道决策算法。该方法现已成功应用在人工智能领域中，例如Atari游戏[11-12]、围棋比赛[13]、机器人路径规划[14]、无人车车道保持问题[15]等。文献[16]使用Q-learning对高速公路车辆的换道决策进行研究，但该研究仅考虑简单的双车道场景，且当输入状态维数过高时，该算法会消耗大量时间，计算效率很低。文献[17-19]使用DQN对高速公路场景中的车辆建模，并对决策成功率和平均奖励等评价指标进行了分析，但由于DQN存在过度估计的问题，使得估计的Q值大于真实Q值，使得在模型测试时不能得到准确的结果，算法往往会收敛到局部最优，同时DQN每次都是从经验回放单元中等概率抽样，导致一些重要的经验样本被忽略，进而降低了算法的收敛速度和网络参数更新的效率。

为了更好地解决无人车换道决策问题，本文提出了一种基于改进深度Q网络的无人车换道决策模型。首先将算法的状态值输入到两个结构相同的神经网络中，并分别计算出估计值和目标值，以此来减少经验样本之间的相关性，进而提升算法的收敛性；然后将隐藏层输出的无人车状态信息同时输入到状态价值函数流和动作优势函数流中，更好地平衡了无人车状态与动作的关系；最后采用PER的方式从经验回放单元中抽取经验样本，以此提升样本的利用率，使得无人车更好地理解周围环境变化，进而得到更加合理的换道决策结果。

1 改进深度Q网络的换道决策模型

1.1 双深度Q网络

双深度Q网络[20]（double deep Q network，DDQN）针对DQN过度估计的问题，将动作的选择和评估进行解耦。首先通过参数为w的主网络选择最大的Q值对应的动作，再使用参数为w′的目标网络计算此动作所对应的目标值，进而对选择的动作进行评估，再根据评估值Q(s j-1,a j-1,w)和目标值计算损失函数L j(w)，并通过误差反向传递的方式更新主网络的参数w，如公式（1）和（2）所示：

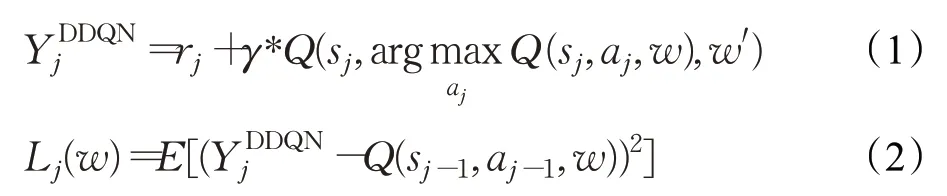
其中为目标值，Q(s j-1,a j-1,w)为评估值，γ为衰减因子，r j为奖励值，损失函数L j(w)根据评估值和目标值的均方误差（mean square error，MSE）计算得到。

1.2 竞争网络结构

基于竞争结构的深度Q网络（dueling deep Q network，dueling DQN）[21]和基于竞争结构的双深度Q网络（dueling double deep Q network，dueling DDQN）分别从DQN和DDQN的基础上在主网络和目标网络中加入竞争网络结构（dueling network architecture），以便更准确的估计Q值，上述两个模型的主网络结构如图1所示。

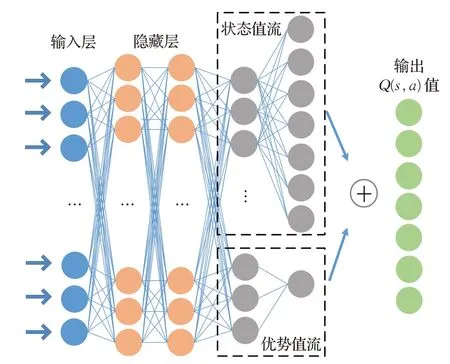
图1 竞争网络结构Fig.1 Dueling network structure

无人车在行驶过程中从周围环境获取状态值作为网络输入，通过隐藏层的状态信息分别被输入到状态价值函数流和动作优势函数流中进行进一步的数据处理，然后将两个函数流的输出相加，最后输出Q(s,a)的值。Q(s,a)的计算方式如公式（3）所示：

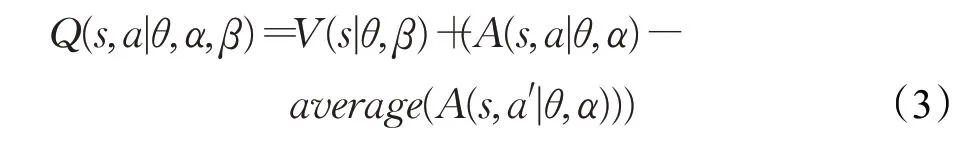
其中Q(s,a|θ,α,β)为输出的Q值，V(s|θ,β)为状态价值函数，A(s,a|θ,α)为动作优势函数，θ为公共隐藏层的网络参数，α为动作优势网络的参数，β为状态价值网络的参数，a′为所有可能采取的动作，average则是对所有动作优势函数取均值。

1.3 优先级经验回放

在无人车与环境不断交互的过程中，经验样本被不断的存储到经验回放单元中用于模型的训练，但不同经验样本之间的重要性是不同的，随着经验回放单元中样本的不断更新，如果采取均匀随机取样的方式从经验回放单元中抽取小批量样本作为模型输入，那么一些重要性较高的经验样本就无法被充分利用甚至被直接覆盖，导致模型训练效率降低。为提升模型的训练效率，使用一种优先级经验回放[22]的方式从经验回放单元中抽取样本，以此增加重要性较高的样本被抽取的概率。即用δj表示样本j的时间差分误差（temporal differenceerror，TD-error），并以此来衡量每个经验样本的重要性，如公式（4）所示：

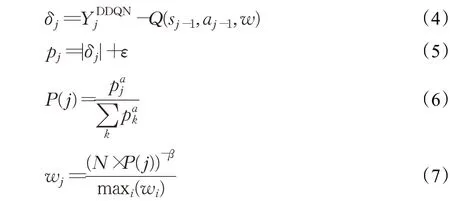
其中p j为样本j的优先级，ε为很小的正常数进而保证TD-error几乎为0的样本也有较低的概率被抽取。P(j)为样本j的优先级权重，α为经验回放时优先级权重所占的比例，若α为0，则采用均匀随机抽样，否则根据归一化后的权重w j抽样。如公式（5）～（7）所示，N为经验回放单元的大小，β为抽样权重系数，取值范围为β∈[0,1]。在抽取样本时通过采用优先级经验回放的方式，提升了主网络误差反向传递时更新参数的效率以及网络的收敛速度。

1.4 改进的深度Q网络

为了使无人车在决策过程中得到更优的驾驶策略，使用改进的深度Q网络建立换道决策算法。此算法先将DDQN与竞争结构结合，并用于主网络和目标网络中来解决DQN过度估计问题，同时更好地平衡了状态价值函数和动作优势函数的关系。然后采用优先级经验回放的方式抽取小批量数据作为模型输入，进一步提升了TD-error的绝对值较大的样本利用效率。基于改进深度Q网络的无人车换道决策算法结构图如图2所示，在无人车的行驶过程中，首先无人车获取自身以及周围车辆的参数信息作为当前时刻的状态值，同时将动作值、无人车与环境交互得到的奖励值、以及下一时刻的状态值作为一个元组，即(s,a,r,s′)，存储到经验回放单元D中，然后使用优先级经验回放的方式进行抽取样本，并将状态值分别输入到主网络和目标网络中，根据两个网络的输出结果以及奖励值r对损失函数进行计算，进而更新主网络的网络参数，直到算法完成迭代。

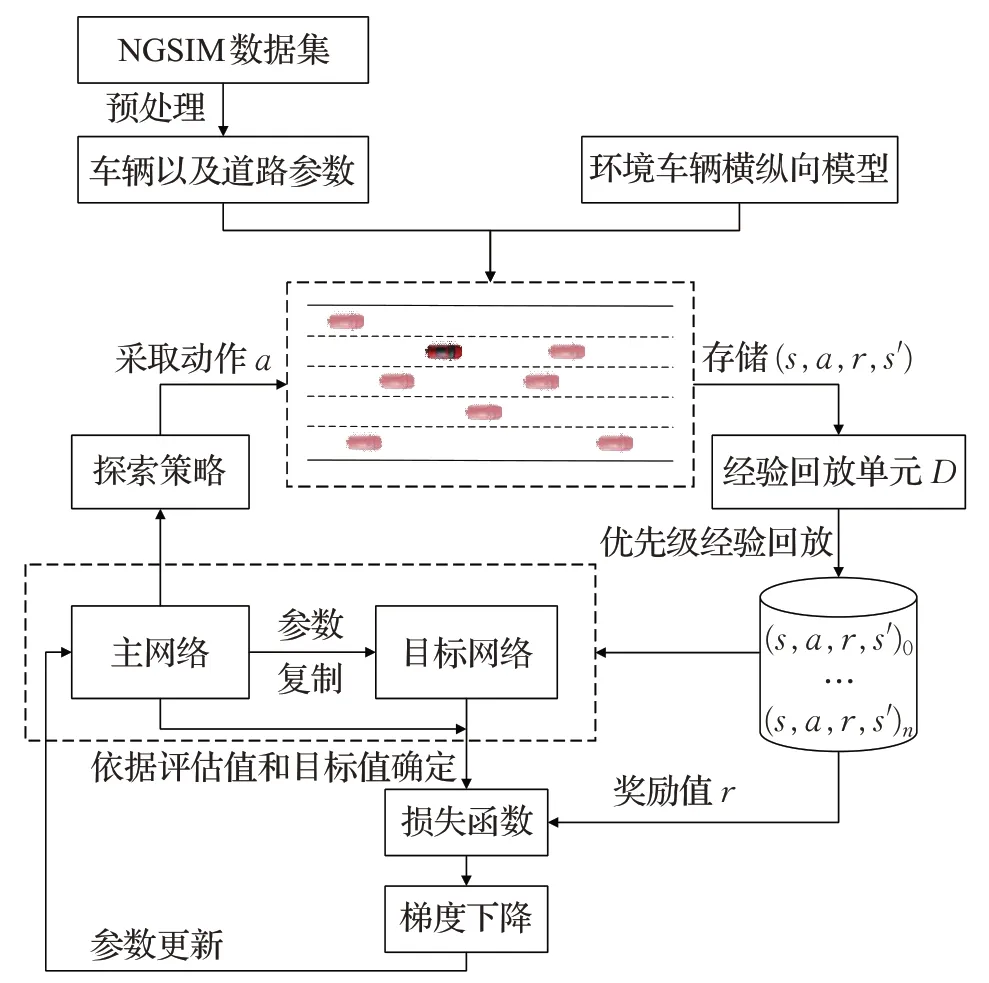
图2 改进深度Q网络的无人车换道决策算法结构Fig.2 Structure diagram of autonomous vehicle lane change strategy algorithm based on improved deep Q network

2 实验场景搭建

实验场景搭建分为数据预处理和环境车辆模型搭建两部分。如图3所示，通过数据预处理对道路环境中的车流量、车辆速度及初速度范围、车辆初始位置进行提取，同时结合环境车辆模型，对真实道路环境进行还原，并将此场景作为算法的训练和测试场景。

图3 US-101高速场景Fig.3 US-101 highway scene

2.1 数据预处理

实验中选用NGSIM数据集中US-101高速公路的车辆数据进行车辆及道路参数的提取。US-101高速公路场景如图3所示，高速路全长约640 m，共有8条车道，其中1～5号车道为主车道，6号车道为辅路道，7、8号车道分别为车流汇入车道和汇出车道。实验中选用主车道（1～5号）中的车辆数据搭建5车道道路实验场景。

首先对主车道车辆数据进行预处理，剔除轿车外的其他车辆类型数据，并筛选出主车道前300 m的车辆数据，该段数据对应的道路中的车流量适中。由于5号车道中的车辆受6～8号车道内车辆汇入和汇出的影响，故分别统计1～4号车道的车辆与5号车道的车流量、车辆速度及初速度范围、车辆初始位置等参数，以便更好地还原真实环境中的道路场景。统计后的车辆数据信息如表1所示，1～5车道车辆速度分布如图4所示，车辆初速度分布如图5所示。

表1 车辆数据信息Table 1 Information of vehicle data

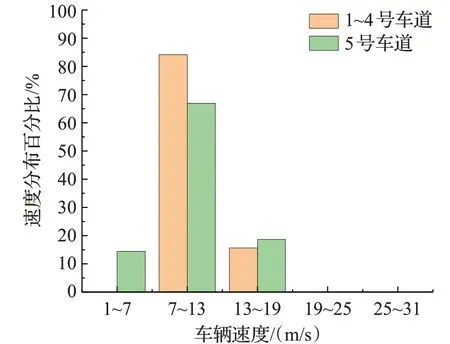
图4 车辆速度分布Fig.4 Vehicle speed distribution

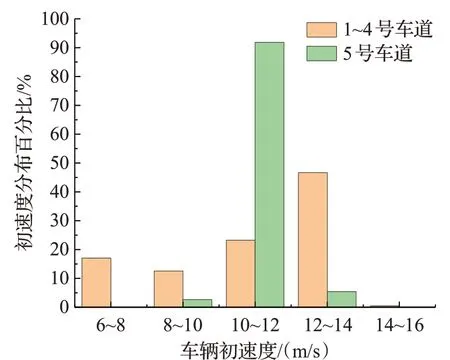
图5 车辆初速度分布Fig.5 Initial vehicle speed distribution

根据表1可知，在900 s内，1～4号车道共有1 502辆车，即车流量约为每分钟100辆；5号车道共有389辆车，即车流量约为每分钟26辆。

根据图4、5可知，1～4号车道的车辆速度范围和初速度范围主要分布在7～19 m/s和6～14 m/s，比例分别达到99.75%和99.51%；5号车道的车辆速度范围和初速度范围主要分布在1～19 m/s和10～12 m/s，比例分别达到99.98%和91.89%。为适应绝大多数车辆的驾驶规律，故使用上述车辆的初速度和速度范围作为车辆仿真环境参数。车辆初始位置可通过数据集直接获取。同时，对主车道车辆的长度宽度进行统计，统计结果为：长度为12 ft（约3.6 m），宽度为6 ft（约1.8 m）的车辆所占比例最大，故选用长3.6 m、宽1.8 m的车辆作为实验仿真车辆。仿真车辆参数如表2所示。

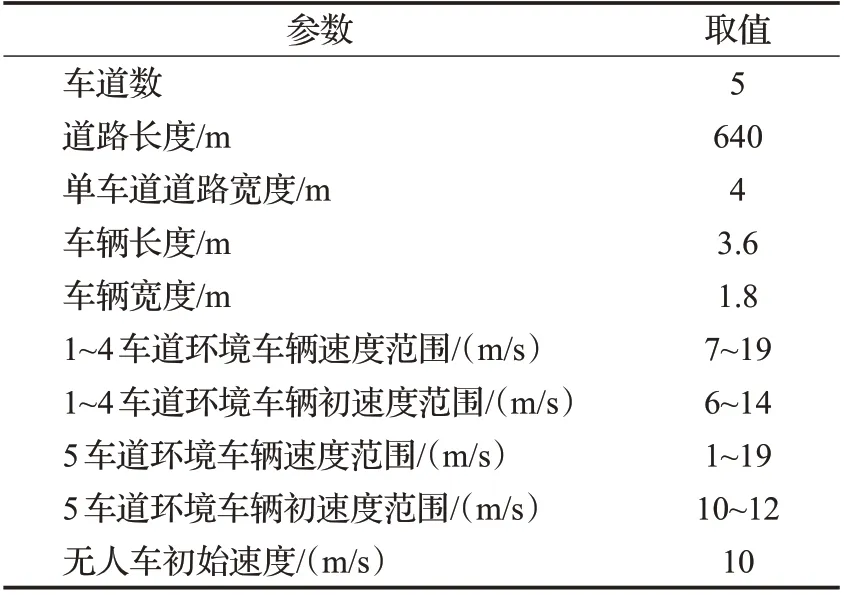
表2 仿真环境参数设定Table 2 Simulation environment parameters setting

2.2 环境车辆模型搭建

为了更好地模拟真实道路环境中车辆的驾驶行为，分别使用车辆横向和纵向模型对实验场景中的环境车辆进行建模。其中横向模型采用MOBIL（minimizing overall braking induced by lane change）模型，使用此策略模型对环境车辆的换道行为进行建模，如公式（8）～（10）所示：

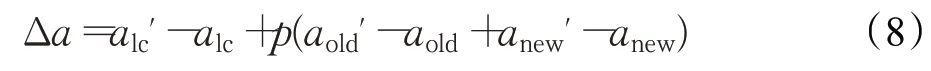
上述公式中，Δa为加速度增益，alc、aold、anew分别为执行换道车辆、换道前原车道的后方车辆以及目标车道后方车辆的加速度，alc＇、aold＇、anew＇分别为以上换道车辆换道后的加速度，p为礼貌因子，该参数描述了环境车辆驾驶的激进程度，取值范围为0～1，b s为保证安全的最大减速度，Δath为决策阈值。若anew＇大于-b s，同时加速度增益Δa大于决策阈值Δath时，环境车辆进行换道操作。

车辆纵向模型采用IDM（intelligent driver model），此模型描述了环境车辆的跟车行为，如公式（11）和（12）所示：

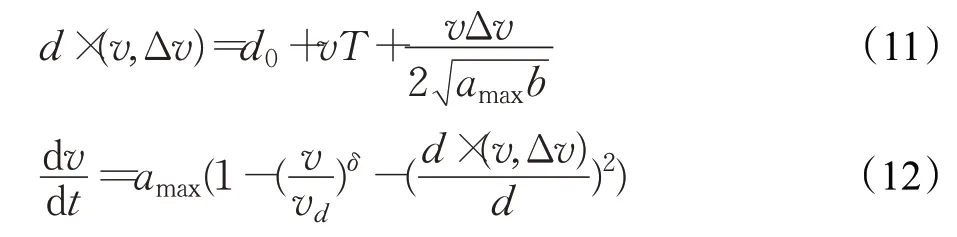
上述公式中，d×(v,Δv)为最小期望间距，d0为最小安全间距，v为车辆当前速度值T为期望安全时距，Δv为同车道当前车辆与前车的速度差，amax为期望最大加速度值，b为期望减速度值，vd为期望速度值，δ为加速度指数。

3 实验结果与分析

3.1 实验环境与参数设定

实验中环境采用Python3.7语言作为编程语言，使用gym库创建实验场景，神经网络框架使用PyTorch1.4.0；计算机配置为：显卡NVIDIA GTX1060，操作系统为Ubuntu16.04，处理器为i7-8750H，内存为16 GB。

设定训练最大回合数为10 000，单回合最大步长为30，道路环境刷新周期为1 s，同时根据上一章节2.1中主车道车流量信息，可知1～4车道的单回合车流量为每回合50辆，5车道的单回合车流量为每回合13辆，单回合终止条件为无人车单回合执行步数达到最大或无人车与环境车发生碰撞，且在实验过程中设定无人车均保持在可行使区域内行驶。算法参数设定如表3所示。

表3 算法参数设定Table 3 Algorithm parameters setting

表3中的衰减因子γ描述的是未来得到的奖励值对当前状态的影响，通过分析实验所有回合中累计步数的分布确定当γ=0.98时，算法的收敛性最好，同时平均奖励值达到最大。学习率的选取通过网络误差和网络的收敛速度确定，实验结果显示当学习率为2.5×10-4时网络的收敛速度最快（算法的平均奖励值在训练2 400回合左右基本稳定），同时算法的成功率最高。记忆库容量和批尺寸的大小通过获得的平均奖励值的网络收敛速度确定，记忆库容量的大小会对网络参数更新效率产生影响；而在批尺寸的大小选取方面：若采取较大的批尺寸则算法容易收敛到局部最小值，若较小时则不利于算法的收敛。实验中分别采用了批尺寸为16、32、64这3个超参数分别进行网络的训练，结果表明当记忆库容量大小为8×104，批尺寸为32时，算法的收敛速度最快，同时获得的平均奖励值最高。优先级权重占比α用来确定从经验回放单元中抽取样本时样本优先级所占的比例，而抽样权重β用来修正优先级回放所带来的误差，实验结果显示当α=0.8，β=0.5时，算法的鲁棒性最好，此超参数组合增加了重要性样本被采样的概率，同时模型的鲁棒性也得到提升。

3.2 实验约束条件设定

结合具体的换道决策场景，分别设定状态空间、动作空间以及奖励函数如下所示。

状态空间：状态空间S描述了无人车与周围环境车辆的驾驶行为信息，以无人车和无人车感知范围内最近的6辆环境车状态值的集合作为状态空间，具体定义如公式（13）所示：

其中vhost为无人车的速度，s1～s6为无人车周围环境车辆的状态值，s={exist,x,y,v x,v y}，exist表示为是否存在此环境车辆，若此车存在，则exist=1，否则exist=0。x为无人车相对于此环境车的横向距离，y为无人车相对于此环境车的纵向距离，v x为无人车相对于此环境车的横向速度，v y为无人车相对于此环境车的纵向速度。

动作空间：动作空间描述了无人车行驶过程中可以采取的动作，具体描述如表4所示。

表4 动作空间表示Table 4 Action space representation

奖励函数：为使无人车学习到最佳的换道决策策略，奖励函数定义如下所示。

若无人车与环境车发生碰撞，则设定碰撞惩罚函数：

设定速度奖励函数：

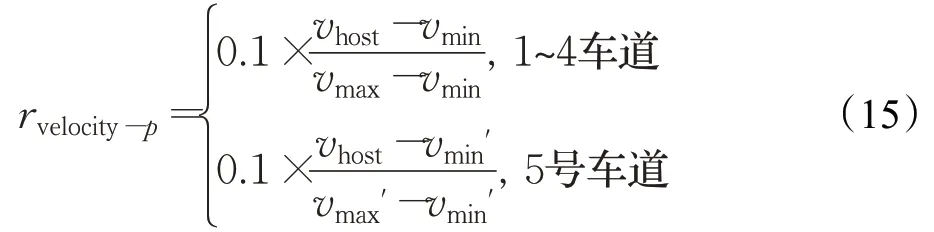
其中vhost为无人车速度，vmax和vmin分别为1～4号车道的最高速度（19 m/s）和最低速度（7 m/s），vmax＇和vmin＇分别为5号车道的最高速度（19 m/s）和最低速度（1 m/s），即若无人车行驶在1～4车道，则取1～4号车道对应的速度奖励值；若无人车行驶在5车道，则取5号车道对应的速度奖励值。

为避免无人车在行驶过程中频繁的变更车道，设定换道惩罚函数：

如果无人车在单个步长内未发生碰撞，则设定单步奖励函数：

如果无人车在整回合内未发生碰撞，则设定回合奖励函数：

单回合总奖励函数R为：

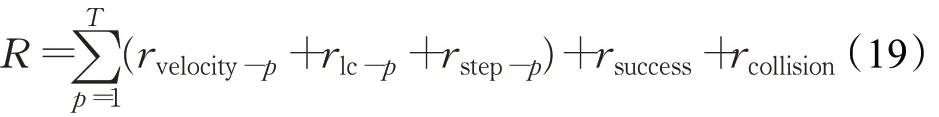
上述公式中，T为单回合执行总步数，p为执行步数。

3.3 算法训练与分析

分别使用DQN、DDQN、Dueling DDQN与本文算法进行实验对比，且4种算法的状态空间、动作空间、奖励函数以及实验参数均保持一致，训练过程中设定环境车辆横向模型参数的礼貌因子p=1。通过分析决策成功率、平均奖励、平均累计步数来描述模型训练结果，4种算法训练的结果随回合数变化趋势如图6～8以及表5所示。

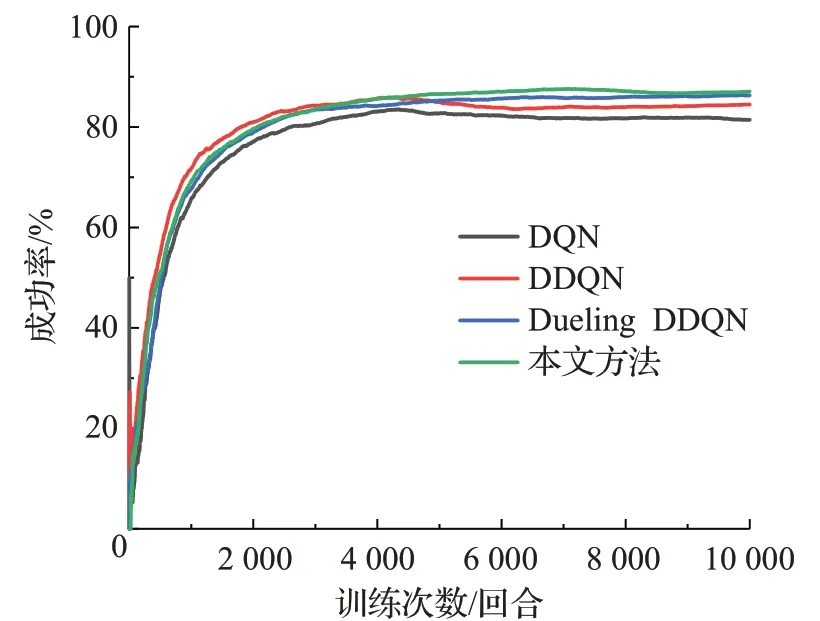
图6 训练过程中各算法的决策成功率对比Fig.6 Comparison of strategy success rate of each algorithm during training process

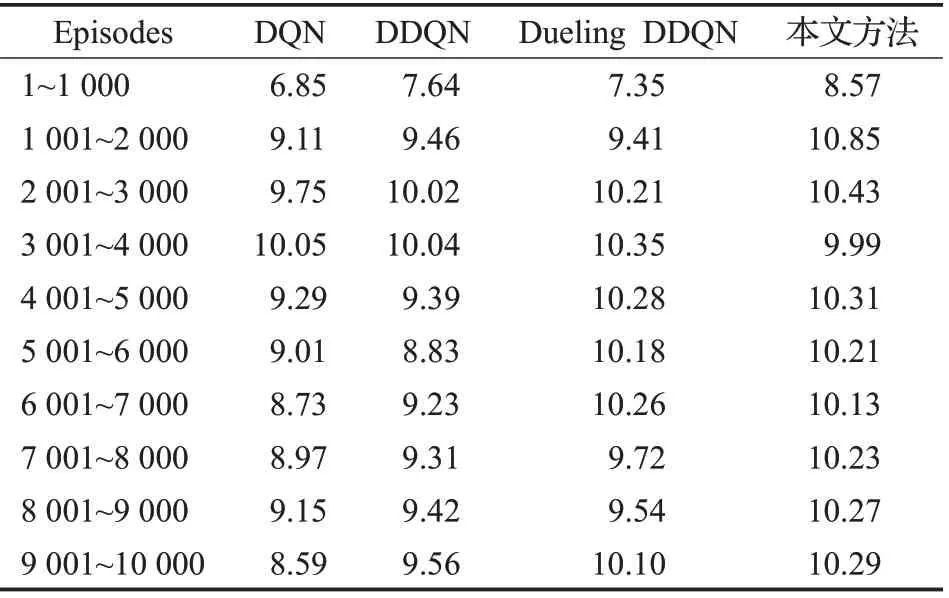
表5 训练过程中各算法平均奖励分布对比Table 5 Comparison of average reward distribution of each algorithm training process

由图6可知，在算法训练开始阶段，4种算法的成功率不断增加，训练10 000回合后，DQN、DDQN、Dueling DDQN、本文方法的成功率依次为：81.43%、84.48%、86.30%、87.09%。本文方法在训练过程中的决策成功率更高。

结合图7和表4可知：在算法训练过程中所获得的平均奖励方面：本文方法在训练结束后的得到的总平均奖励最高，为10.14，且平均奖励值在2 400回合左右基本稳定，而其他方法均在5 500回合后逐渐趋于稳定状态，算法稳定时的回合数约为本文方法的2.29倍。同时该方法在1 001～2 000回合内的平均奖励达到最高，为10.85，Dueling DDQN、DDQN、DQN依次降低，分别为9.74、9.29、8.95，且平均奖励峰值均分布在3 001～4 000回合范围内。由此可见，本文方法可以在更少的训练回合数内完成对算法的训练并获得更高的平均奖励值。同时由于改进的深度Q网络在经验回放时提高了重要程度较高的样本的利用率，增加这些样本的抽样概率。本文方法与DQN、DDQN、Dueling DDQN相比提升了网络的收敛速度和参数更新的效率，同时提高了智能体的学习速度。

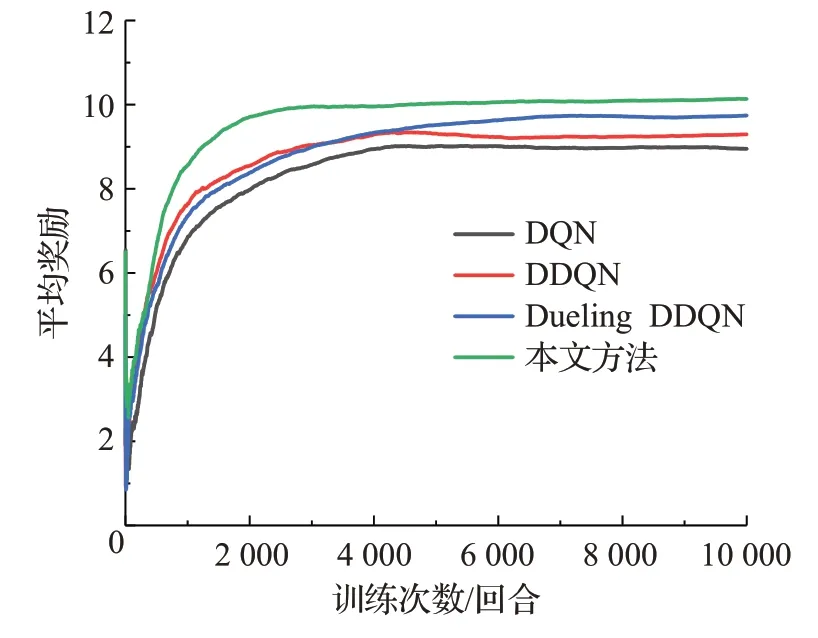
图7 训练过程中各算法的平均奖励对比Fig.7 Comparison of average reward of each algorithm during training process

由图8可知，在1 000回合训练后，本文方法的平均累计步数均高于DQN等网络模型，说明本文方法单回合执行步数最高，同时结合图6可知，本文方法在保持决策成功率最高的同时，平均累计步数较DQN、DDQN、Dueling DDQN分别高出3.14、2.17、1.60，由此说明本文方法具有更好的学习能力和更强的适应性。

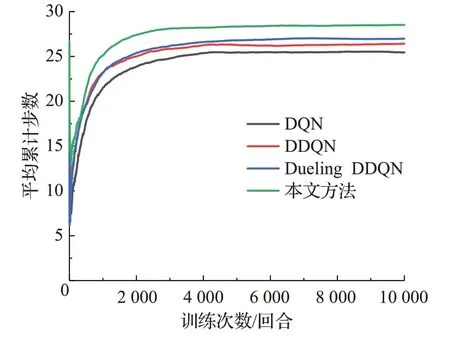
图8 训练过程中各算法的平均累计步数对比Fig.8 Comparison of average cumulative steps of each algorithm during training process

3.4 算法测试与分析

针对不同道路场景中环境车辆，通过改变环境车辆车流量，以及环境车辆横向模型中的礼貌因子p，进而搭建车辆环境不同的实验场景，设定测试回合数为1 000，同时保持其他仿真环境参数和网络参数不变。其中p∈[0,1]，该参数越接近0说明环境车辆驾驶风格越激进。通过改变上述两个参数，设定两个道路环境不同的测试场景，具体描述如下所示。

3.4.1 算法测试场景一

测试场景一使用与算法训练时相同的场景，即1～4车道和5车道的单回合车流量分别为50辆/回合，和13辆/回合，礼貌因子p=1。4种算法在场景一中测试成功率和平均奖励如图9、10所示，测试1 000回合后的结果如表6、7所示。

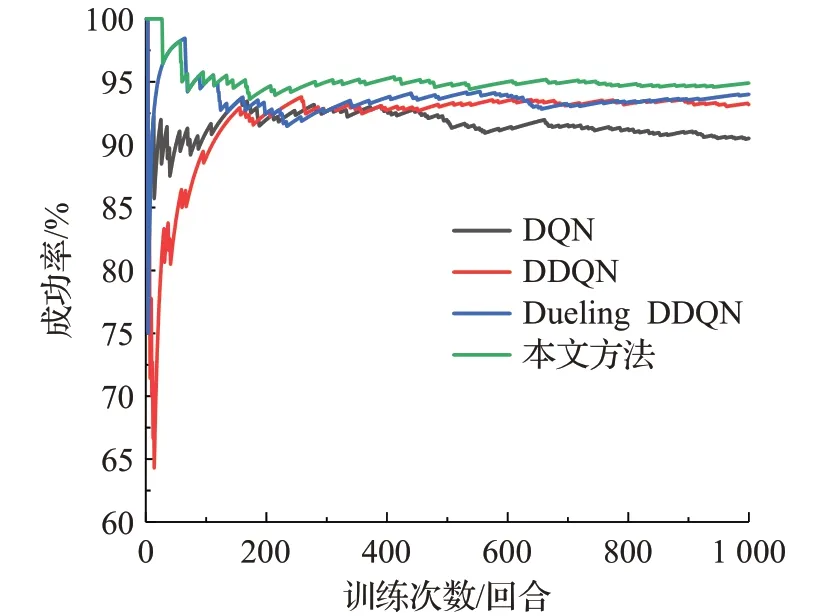
图9 场景一测试过程中各算法的决策成功率对比Fig.9 Comparison of strategy success rate of each algorithm during test processin scenario one

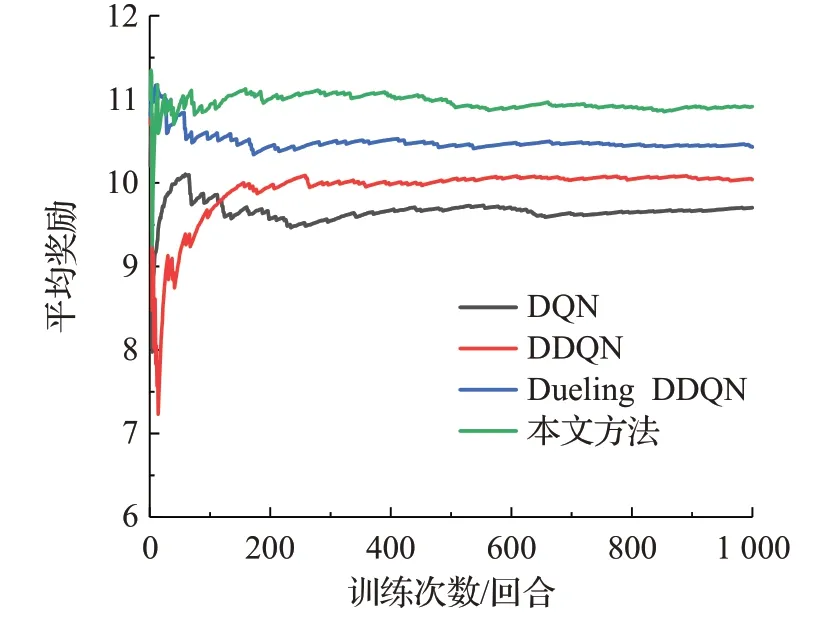
图10 场景一测试过程中各算法的平均奖励对比Fig.10 Comparison of average reward of each algorithm during test processin scenario one

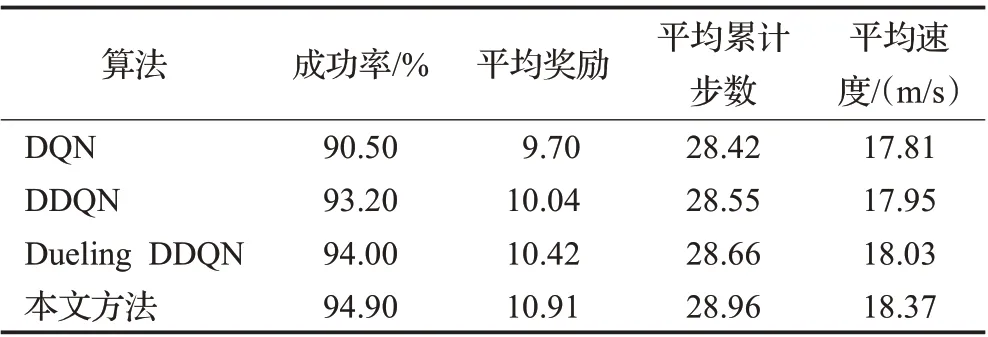
表6 场景一各算法测试结果对比Table 6 Comparison of test results of each algorithm in scenario one

由图9、10和表6可知，在场景一的测试过程中，本文方法较Dueling DDQN、DDQN、DQN在成功率方面分别高出0.9、1.7、4.4个百分点，在平均奖励、平均累计步数、平均速度方面本文方法也均高于其他方法。4种算法在测试1 000回合中的成功次数分别是：DQN为905次、DDQN为932次、Dueling DDQN为940次、本文方法为949次；同时结合表7分析可得：在各算法测试成功回合中，本文方法的单回合奖励值高于11.3的回合所占百分比最高，为78.29%。而单回合奖励值低于11.3的原因是由于无人车在一段时间内为避免碰撞而保守行驶，使得在单回合内获得的奖励值较低。由此说明本文方法可以更好地根据经验回放单元中的经验样本来理解测试环境中车辆的状态变化，在保证决策成功率的前提下减少了保守行驶的回合数，使得无人车获得更优的决策策略。

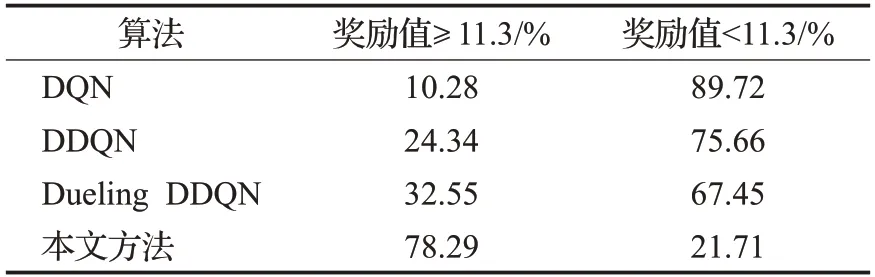
表7 场景一各算法成功回合中奖励值分布比例Table 7 Proportion of reward value distribution in successful rounds of each algorithm in scenario one

3.4.2 算法测试场景二

测试场景二设定礼貌因子p=0.4，环境车辆的车流量采用US-101道路中车流量较大的部分，即1～4号车道和5号车道的车流量分别约为126辆/min和48辆/min，即单回合车流量分别为63辆/回合和24辆/回合。4种算法在场景二中测试成功率和平均奖励如图11、12所示，测试1 000回合后的结果如表8、9所示。

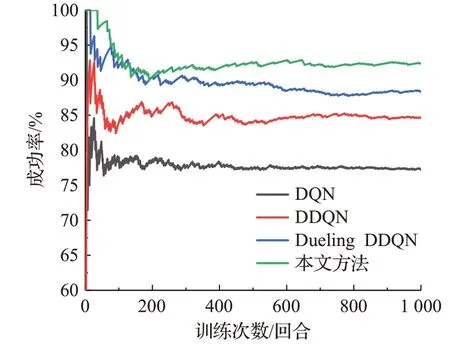
图11 场景二测试过程中各算法的决策成功率对比Fig.11 Comparison of strategy success rate of each algorithm during test processin scenario two

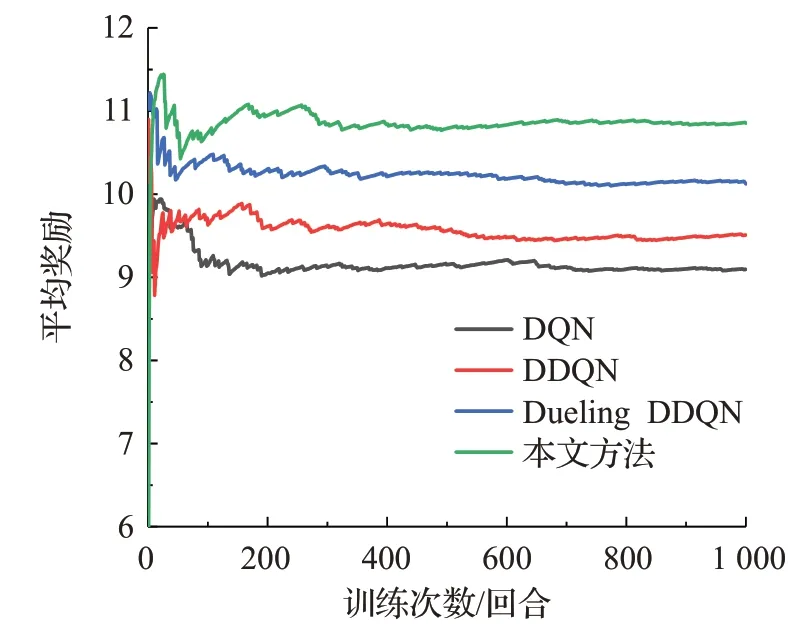
图12 场景二测试过程中各算法的平均奖励对比Fig.12 Comparison of average reward of each algorithm during test processin scenario two

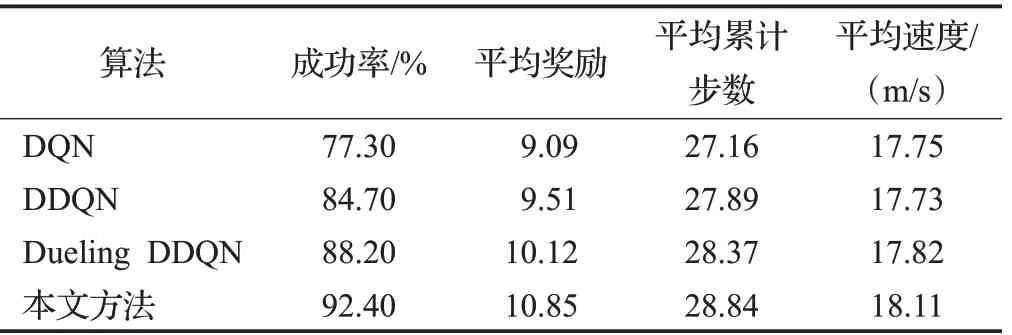
表8 场景二各算法测试结果对比Table 8 Comparison of test results of each algorithm in scenario two

结合图11、12和表8分析可知，在场景二的测试过程中，本文方法较Dueling DDQN、DDQN、DQN在成功率方面分别高出4.2、7.7、15.1个百分点，在平均奖励、平均累计步数、平均速度方面本文方法也均高于其他方法，且4种算法在测试1 000回合后的平均奖励为10.85、10.12、9.51、9.09，与场景一中的测试结果相比，各算法的平均奖励分别下降了0.06、0.30、0.53、0.63，成功率分别下降了2.5、5.8、8.5、13.2个百分点。其中DQN下降幅度最大，原因是DQN使用最大化的方法来计算目标值，这样的计算方式往往使得算法得到次优的决策策略，同时DQN等概率的抽样方式使得一些重要性较高的经验样本被忽略，从而降低了训练过程中网络参数的更新效率，最终导致DQN在更复杂的场景中的测试结果的成功率和平均奖励较低。

由表9可知，在各算法发生碰撞的回合中，本文方法单回合执行步数小于10的回合数（单回合执行步数为30）所占比例最低，为6.58%，Dueling DDQN、DDQN、DQN依次升高，为16.10%、59.48%、66.08%。其中DQN和DDQN单回合执行步数小于10的比例分别是本文方法的10.04倍和9.04倍，由此可见，DDQN和DQN的碰撞相对集中发生测试过程的前三分之一阶段，说明这两种算法的适应性较差，无法根据测试过程中环境车辆的状态变化做出最优的动作。

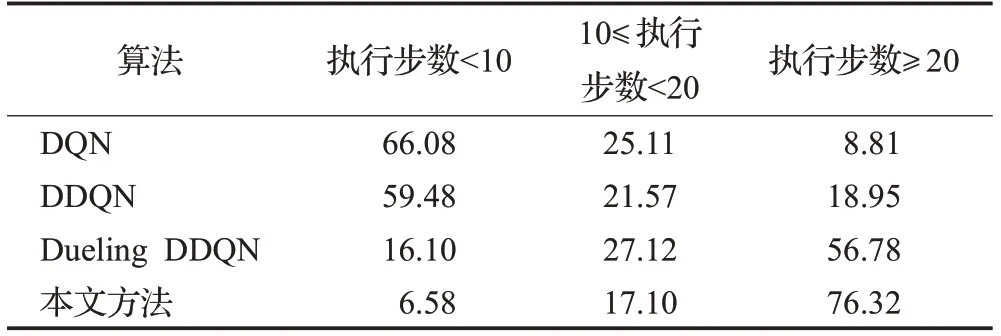
表9 场景二各算法碰撞回合中单回合步数分布比例Table 9 Proportion of reward value distribution in successful rounds of each algorithm in scenario two%

对比场景一和场景二的测试结果可知，4种算法的得到平均奖励均有所下降，原因是随着测试场景的复杂程度增加，导致无人车换道决策的成功率和平均速度的下降，同时无人车发生碰撞的次数增多，使得单回合内获得的步数奖励减少，最终导致平均奖励的下降。

3.4.3 算法测试场景三

测试场景三设定礼貌因子p=0，环境车辆的车流量采用US-101道路中车流量最大的部分，即1～4号车道和5号车道的车流量分别约为144辆/min和64辆/min，即单回合车流量分别为72辆/回合和32辆/回合。4种算法在场景三中测试1 000回合后的结果如表10所示。

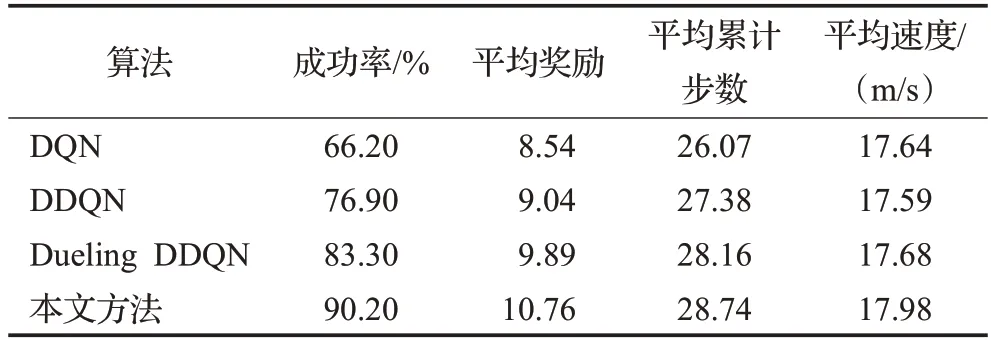
表10 场景三各算法测试结果对比Table 10 Comparison of test results of various algorithm in scenario three

由表10可知，在场景三的测试过程中，本文方法较Dueling DDQN、DDQN、DQN在成功率方面分别高出6.9、13.3、24.0个百分点，在平均奖励、平均累计步数、平均速度方面本文方法也均高于其他方法，且4种算法在测试1 000回合后的平均奖励为10.76、9.89、9.04、8.54，与场景二中的测试结果相比，各算法的平均奖励分别下降了0.09、0.23、0.47、0.55，成功率分别下降了2.2、4.9、7.8、11.1个百分点。随着测试场景环境车辆车流量的增大，场景的复杂程度增加，本文方法的成功率和平均奖励下降幅度最小，说明该方法对于复杂环境的适应性更强，这是由于加入了优先级经验回放的机制，使得重要性更高的样本被抽取的概率增加，进而增加了算法训练时的网络参数的更新效率，同时竞争结构的存在使得该算法在更新主网络参数时价值函数被优先更新，导致在当前状态下所有的Q值均被更新，从而更准确地得到了每个动作所对应的Q值。

对比3种场景中各算法的测试结果，如表11所示。

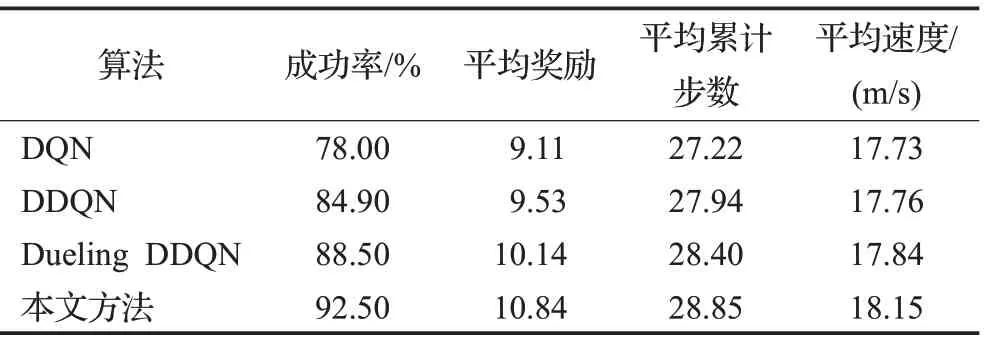
表11 3种场景中各算法测试的平均结果对比Table 11 Comparison of average results of each algorithm test in three scenarios

由表11可知，在3种场景的平均测试成功率方面，本文方法最高，为92.50%，比Dueling DDQN、DDQN和DQN算法的分别高出4.0、7.6、14.5个百分点；在平均奖励方面，本文方法最高，为10.84。由此说明，本文方法可以更好地理解外部环境状态的变化，同时具有更好的鲁棒性和更强的适用性。

4 结束语

针对传统DQN在高速公路场景下的无人车换道决策中存在过估计且收敛速度较慢的问题，本文提出一种基于改进深度Q网络的无人车换道决策模型。首先将得到的无人车与环境车的状态值分别输入到主网络和目标网络中，进而将动作的选择和评估解耦，提高了网络的稳定性，解决了网络的过估计问题；然后在网络中加入竞争结构，使模型对动作价值的估计更加准确；最后通过增加重要样本被回放的概率，提升网络的更新效率和收敛速度。实验结果表明，相比于传统DQN等算法，改进的深度Q网络在训练和测试的决策成功率、平均奖励、平均累计步数方面上均有提升；测试结果也表明，该方法的鲁棒性更强，在车流量更大、环境车辆驾驶风格更激进的测试场景中仍能保持92%以上的换道决策成功率。

虽然本文算法在不同场景的测试结果中均能保持较高的换道决策成功率，但只能应对离散的动作空间问题，接下来的研究将聚焦于使用Actor-Critic的强化学习方法，以此来应对连续动作空间中的无人车换道决策问题。