量子群智能优化算法综述

安家乐，刘晓楠，何 明，宋慧超

信息工程大学 数学工程与先进计算国家重点实验室，郑州 450000

大自然为解决现实世界的问题提供了很多灵感，在与最优化问题领域结合的过程中诞生了群智能优化算法[1]。最优化问题即在一定约束条件的限制下寻找满足需求的最优解，是典型的NP难问题。在现实生活中最为常见的就是离散的组合优化问题，如旅行商问题、背包问题、图着色问题、车辆路径问题等[2]。传统的优化算法通常是用来解决目标函数表达式已知的最优化问题，如梯度下降法、牛顿法等[3]。但在最优化问题日益复杂的现在，由于目标函数连续性差、微分难度大等原因，传统的优化算法已经无法满足需求，尤其是很多问题并没有确定的目标函数表达式或者函数不唯一。在这种情况下，群智能优化算法展现出了它强大的能力。其历史可以追溯到20世纪60年代进化策略的出现以及70年代遗传算法的诞生[4]，在20世纪90年代取得了迅猛发展。在过去的二三十年间，大量的群智能优化算法被提出，典型的有蚁群优化算法、粒子群优化算法、人工蜂群算法以及萤火虫算法等等[5～10]。它们在解决最优化问题上有着很好的表现，但随着研究问题的日益复杂，在求解过程中仍存在计算时间过长以及易陷入局部最优等不足。

量子计算是一个快速发展的领域，其概念最早是在20世纪80年代由Feynman提出[11]，一经提出便引起诸多学者的广泛关注，近年来在许多方向上取得了突破。量子计算的基础是量子比特，与经典计算机的0、1比特不同，量子比特位可以处于0和1的叠加态。基于量子计算独有的叠加、纠缠以及干涉等特性，量子算法展现出了天然的并行性以及在一些问题上实现指数加速的潜力，较成功的算法有Shor算法以及Grover算法等[12-13]。在最优化领域，也出现了量子计算与群智能优化算法结合而成的量子群智能优化算法。量子群智能优化算法的历史最早可以追溯到1996年，文献[14]首次提出将量子计算和遗传算法结合，形成了全新的量子遗传算法，用于解决TSP难题。但是，文章所提出的算法并没有很好的利用量子计算。直到2000年，文献[15]才正式提出了量子遗传算法，用于解决0-1背包问题。相比之前的算法，文献[15]首次引入了量子比特和量子旋转门的概念分别实现染色体进行编码和更新。遗传算法虽然严格来说不属于群智能优化算法，但两者十分相似，有着极为特殊的联系。因此，量子遗传算法的诞生也掀起了量子计算与群智能优化算法结合的热潮。

经过二十多年的蓬勃发展，许多量子群智能优化算法被提出。这些算法主要包括：Sun等[16]的量子粒子群优化（quantum particle swarm optimization，QPSO）算法、李盼池等[17]的连续量子蚁群算法（quantum ant colony algorithm，QACA）、唐涛[18]的量子人工鱼群算法（quantum artificial fish swarm algorithm，QAFSA）、Gao等[19]的量子蜂群优化（quantum bee colony optimization，QBCO）算法等。一些新的基于量子特性的群智能优化算法也随之出现，包括：量子布谷鸟搜索算法[20]（quantum cuckoo search algorithm，QCSA）、量子混合蛙跳算法[21]（quantum shuffled frog leaping algorithm，QSFLA）、量子萤火虫算法[22]（quantum firefly algorithm，QFA）、量子蝙蝠算法[23]（quantum bat algorithm，QBA）等，未来也将会有更多的新型算法被提出。

很多研究基于最基础的量子群智能优化算法进行了许多改进，提出了很多变体，并应用于解决不同领域的现实世界问题。算法的研究大多关注于解决难题，包括信号处理、控制系统、生物医学工程、电力系统、安全、数据通信、安全、计算机网络等领域。根据不同的量子群智能优化算法具有的不同特性，对它们进行理论分析、改进以及组合。许多研究者也研究了这些算法的参数设置，以获得更好的性能。

在接下来的内容中，本文将聚焦于介绍各类量子群智能优化算法，比较它们的不同方面，并系统的总结面临的问题与挑战。

1 量子群智能优化算法概览

本章对基于量子群智能的计算算法的研究工作进行简要介绍。概略分析了几种经典的量子群智能优化算法：量子蚁群算法、量子粒子群算法、量子人工鱼群算法、量子人工蜂群算法、量子布谷鸟搜索算法，以及部分新型量子群智能优化算法：量子混合蛙跳算法、量子萤火虫算法和量子蝙蝠算法等典型的量子群智能算法，其部分特点如表1所列。这些算法有着不同的操作方式和控制参数。但是，基于量子群智能的计算算法的基本操作通常都包括初始化、更新、求值和选择。表2则对这些算法的优缺点以及应用场景进行展示。

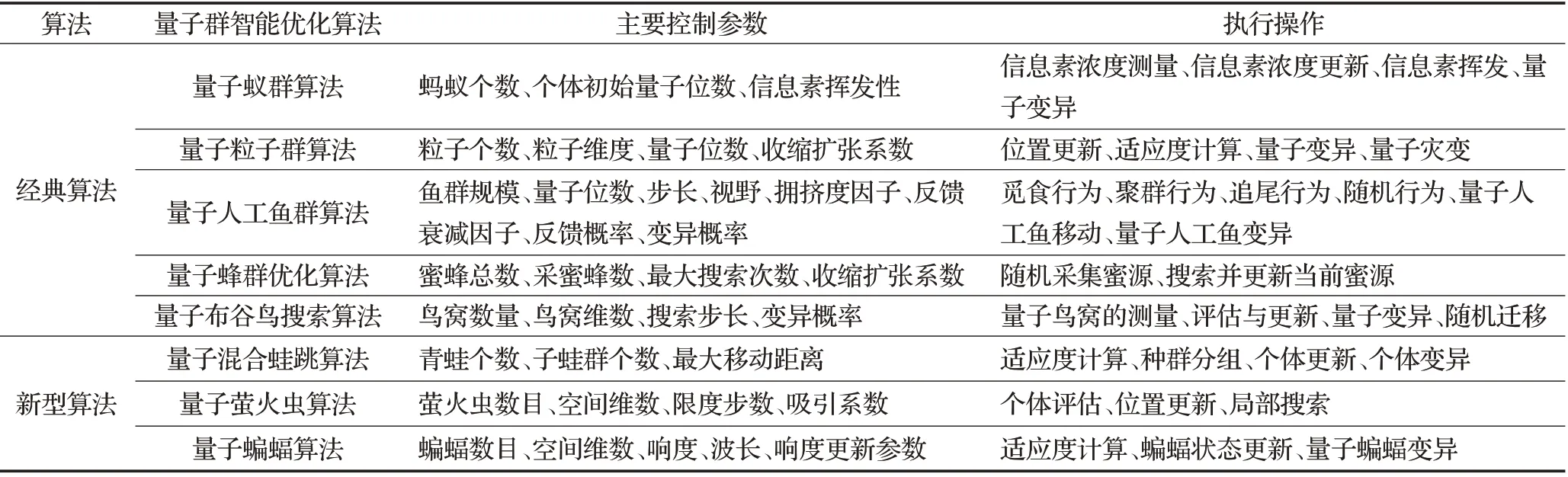
表1 几种典型的量子群智能优化算法的特性Table 1 Characteristics of several typical quantum swarm intelligence optimization algorithms

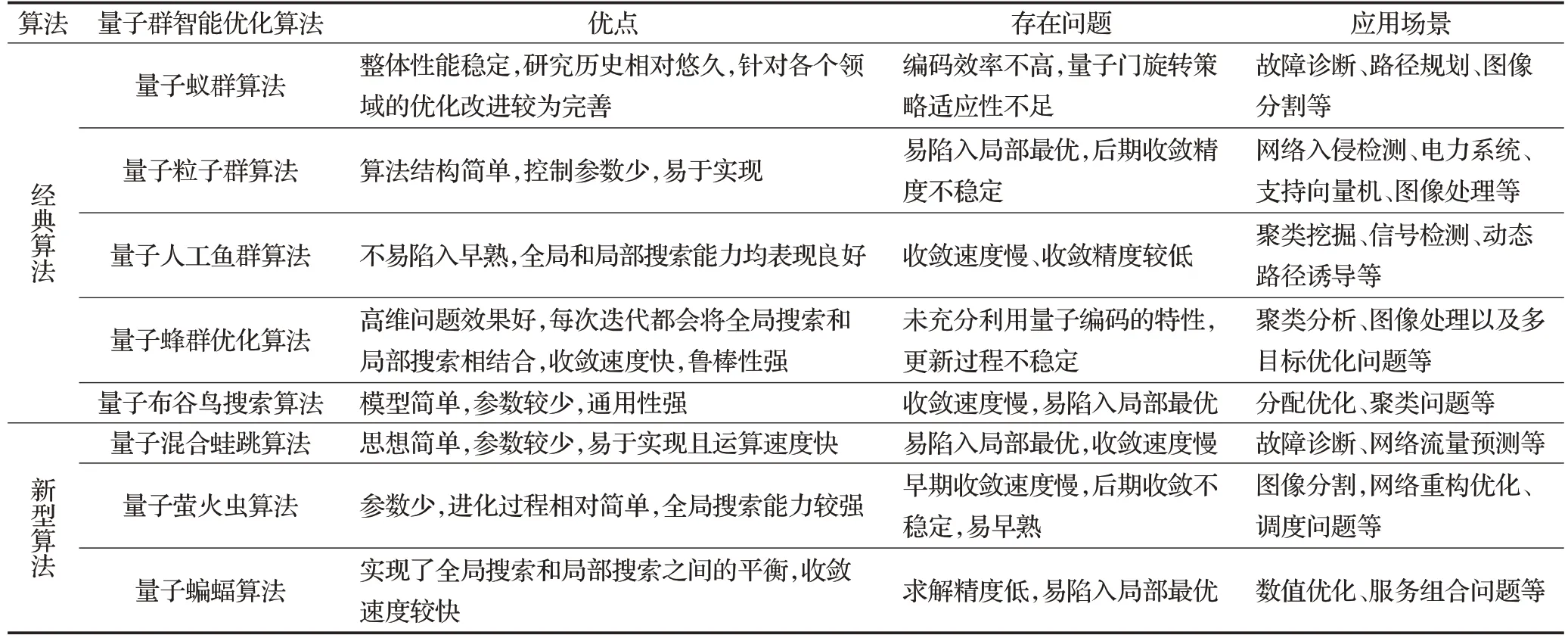
表2 算法的优缺点及应用场景Table 2 Advantages，disadvantages and application scenarios of algorithms

2 典型的量子群智能优化算法

本章对前一章中概览的量子群智能优化算法分别进行了更为详细的介绍，并对其研究现状和改进思路做出了综述。

2.1 量子蚁群算法

量子蚁群算法（QACA）是由经典的蚁群算法与量子计算思想结合而成的。与蚂蚁本身类似，蚁群算法基于由信息素实现的蚁群内部间接的信息交换。量子蚁群算法则是在蚁群算法的基础上，使用量子比特对蚂蚁群体进行编码，量子旋转门等进行更新。量子蚁群算法最早由Narayanan和Moore定义，在2008年为了解决连续空间中的优化问题，由李盼池等[17]首次实现，也是第一次引入了利用量子非门实现的变异操作。与解决组合优化问题不同，这时的连续量子蚁群算法（CQACA）中蚂蚁释放的信息素是位于当前所在的位置点的，而并非其经过的全部路径。CQACA是具有启发性的，它为后续的应用以及算法的变体提供了一个框架。随着优化问题及现实情况的不断变化，李盼池等[17]的文章也被频繁引用和改进。目前，QACA已经广泛应用于最短路径问题（short path problem，SPP）、旅行商问题（traveling salesman problem，TSP）、图着色问题（graph coloring problem，GCP）和0-1背包问题（0-1 knapsack problem，0-1KP）等NP难问题[24～27]。

在量子蚁群算法中，针对不同问题首先用m个量子比特对每条路径的信息素进行初始化编码，最多可以同时处于2m个状态。一只蚂蚁遇到节点的岔路口时，可以检测到不同路径的信息素浓度，在运动之后也会增强所选路径的信息素浓度，一只蚂蚁的运动轨迹被邻近的蚂蚁根据信息素的浓度观测到。信息素越多，蚂蚁选择这条路径的可能性越大，信息素浓度的更新由量子旋转门完成，最终由蚁群共同标记出一条最短路径。

2.1.1 研究现状及应用

Chen等[28]结合量子进化算法和蚁群算法，将蚂蚁的位置信息用量子Bloch球面坐标进行了编码，并设计了一种新的旋转方法进行更新，在对TSP等问题的仿真上取得了较好的效果。王灵等[29]提出一种自适应的旋转角更新策略，在算法的不同阶段使用不同大小的旋转角对种群进行更新，算法前期旋转角较大以加快搜索速度，算法后期根据收敛情况减小旋转角的度数，避免在最优值附近横跳，提升了收敛的准确性。李絮等[30]则利用量子信息纠缠和干涉的特性引入了一种量子交叉策略，促进种群内部的信息交流，增加种群的多样性，只在算法陷入停滞状态时使用，避免算法陷入局部最优无法跳出。贾瑞玉等[31]针对QACA求解较大规模问题时易陷入停滞状态，提出了一种混合量子蚁群算法，设计了一种新的变换邻域准则对求得的解进行优化，避免陷入局部最优，仿真结果表明，该算法在面对较大规模问题时具有更好的收敛速度和求解精度。张程程[32]将Hadamard门引入变异机制，不再使用传统的非门实现个体变异，在旋转过程中不仅实现了赋值互换，还改变了其大小，扩大了种群多样性。Xia等[33]为实现多目标的路径规划，利用多条启发式信息确定蚂蚁的迁移规则和迁移概率，通过量子位对信息素进行编码，量子信息素通过算法中的局部和全局更新规则进行更新。

通过在基本量子蚁群算法的基础上进行适当修改和对一些步骤的改进适配，量子蚁群算法已经被应用于各种不同的优化问题，如故障诊断[34]、WSN[35]、AGVS路径规划[36]、医疗图像阈值分割[37]、油田水淹层识别[38]、压力容器优化[39]等等。可以发现，这些改进过的量子蚁群算法在有效性和效率方面比经典的蚁群算法好得多，量子蚁群算法在这些领域已经显示出了其巨大优势，并将被广泛地应用于新的领域和问题。对改进QACA的总结见表3。

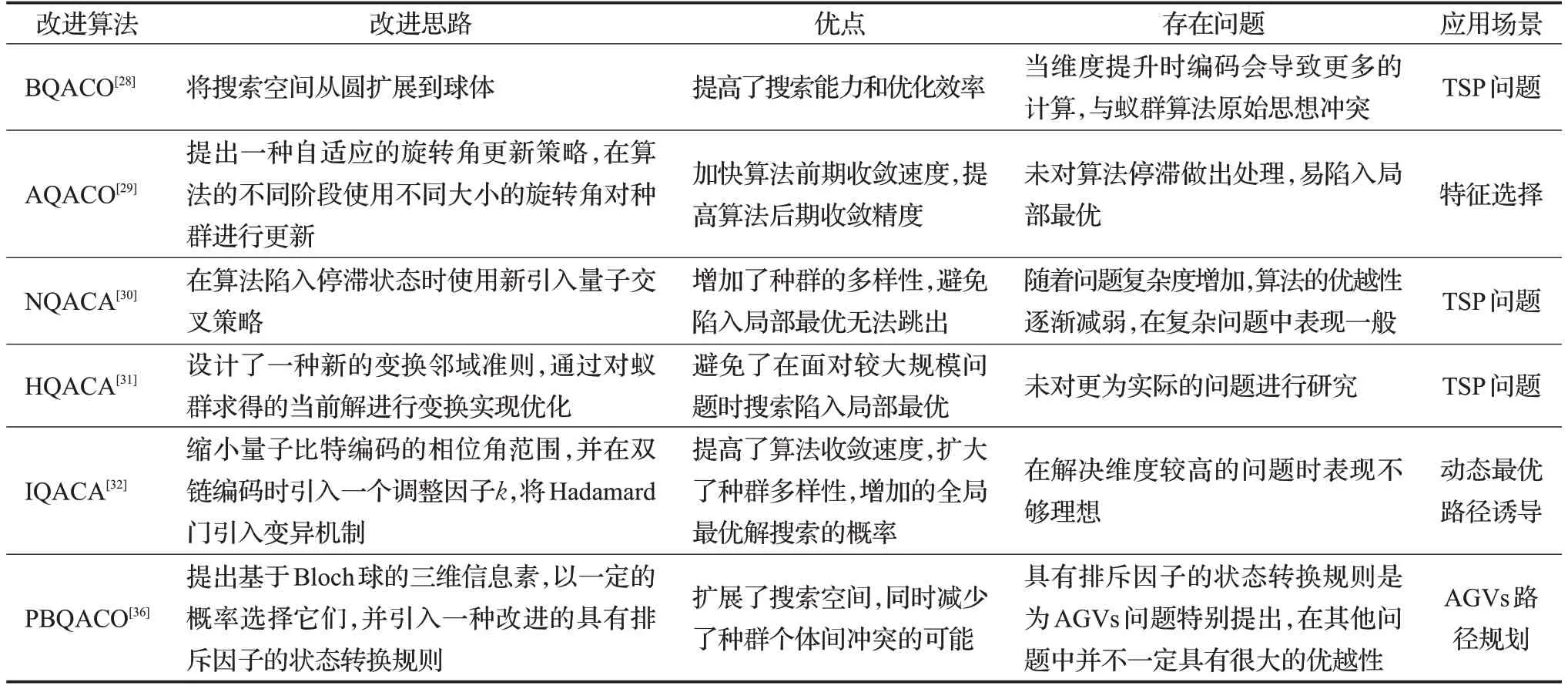
表3 改进量子蚁群算法的优缺点和应用Table 3 Advantages and disadvantages of improved quantum ant colony algorithms and its applications

2.1.2 QACA总结及其局限性

量子蚁群算法将量子计算引入了蚁群算法，利用量子信息的并行特性以较小的种群规模更充分的利用搜索空间，通过量子旋转增加种群的多样性，应对蚁群算法易陷入局部最优的缺点。量子蚁群算法的核心在于引入量子编码和量子旋转门的概念，但其仍只是蚁群算法的一种优化，本质还是蚁群算法，并不能完全避免蚁群算法固有的缺陷。现有的优化多从编码方式、量子门构造、旋转角策略调整以及引入新操作等方面进行改进，以加快搜索速度并提高算法的稳定性，提高算法的全局搜索能力和局部搜索的有效性。

目前量子蚁群算法在简单组合优化问题上成果显著，但是如果是通过简单的投影测量及变换解空间的方式将量子位转换成经典比特位，那么算法将不适合多参数优化以及高精度计算。因此对适用于高维优化问题的量子蚁群算法的研究是颇为重要的。同时，对其数学理论方面的研究尚不完善，无论是参数设置还是收敛性的理论分析都停留在浅显的层面。缺少基础领域的理论使得算法的研究与优化无法真正的脚踏实地，因此算法的数学理论层面更需要研究者们关注。

2.2 量子粒子群优化算法

与量子蚁群算法相似，量子粒子群优化（QPSO）算法是由量子计算和群智能优化算法之一的粒子群优化算法结合而成。粒子群优化算法源于对鸟群、鱼群自然行为的模拟，是粒子群基于内部协作来搜索全局最优点的过程。2004年，Sun等[16]针对粒子群优化算法智能程度低、易早熟等缺点，首次提出了量子粒子群优化算法，利用具有量子特性的粒子对群体智能行为进行模拟。目前，量子粒子群优化算法已经被应用于解决各种复杂的优化问题，例如网络入侵检测[40]、电力系统[41]、支持向量机[42]和图像处理[43]等等。

量子粒子群优化算法的最大优点是相较其他量子群智能优化算法，其算法结构十分简单，易于实现，主要在于其控制参数少。除去种群规模、迭代次数等基本参数，需要人为进行设置的只有一个收缩扩张系数β。并且由于粒子具有量子特性，其运动不受轨道约束，能够更好地进行全局搜索。

2.2.1 研究现状及应用

近年来，研究者们提出了各种量子粒子群优化算法模型。Radha和Gopalakrishnan[44]利用全面搜索策略概念对QPSO做出改进，通过驻留搜索策略寻找新粒子来防止由于过强的吸引导致的过早收敛，同样的通过综合搜索策略识别新粒子，提出了IQPSO（improved quantum particle swarm optimization）与LSM结合用于提高医学图像分割的稳定性和细致性。Zhao等[45]基于差分进化算法的快速收敛性和遗传算法算法交叉算子的粒子多样性，提出了一种差分进化交叉量子粒子群优化（differential evolution-crossover quantum particle swarm optimization，DE-CQPSO）算法，提高全局搜索能力，提供一种改进的自适应方法来控制交叉概率的更新，克服QPSO算法收敛的不稳定性和在特殊情况下陷入局部最优的偶然性，并用以解决环境经济调度问题。金鹏[46]提出了一种势阱长度自适应并且融合了社会学习和莱纳飞行的QPSO（ALSL-QPSO）算法，利用社会学习策略更新非最优粒子，加强算法的全局搜索能力，同时通过莱纳飞行策略解决最优粒子不更新的问题，提高了种群多样性，再实现自适应的调节势阱长度，进一步提高算法的全局搜索能力和局部挖掘能力。赵国新等[47]利用差分策略影响粒子位置的更新，使粒子更好地向最优位置靠近，引入Levy飞行策略增加种群的多样性，降低了算法陷入局部最优的可能，同时自适应的调整收缩-扩张系数β，增强算法前期搜索速度以及后期的收敛精度。对改进QPSO算法的总结见表4。

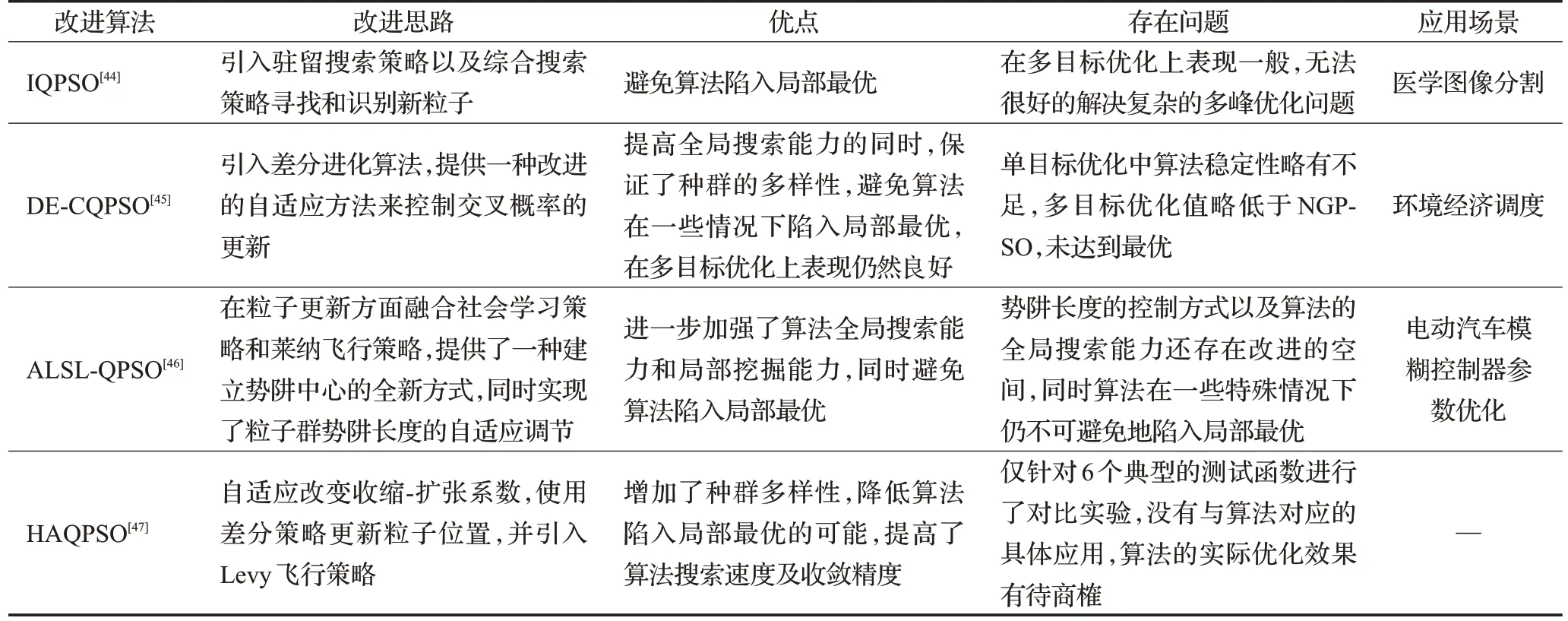
表4 改进量子粒子群优化算法的优缺点和应用Table 4 Advantages and disadvantages of improved quantum particle swarm optimization algorithms and its applications

2.2.2 QPSO算法总结及其局限性

量子粒子群优化算法自提出以来便广为研究者们所关注，而它在实际应用中也确有其独特的优越性，最为典型的就是极少的控制参数。然而即使利用量子特性对PSO算法进行了优化，量子粒子群优化算法在实际应用中仍存在着易陷入局部最优、后期收敛精度不稳定等问题。针对以上问题，目前的改进集中在收缩扩张系数β的适应性调整、引入新算子以及融合其他策略和思想。目前研究取得了一定的成果，但是优化算法没有最好，只有更好，针对QPSO算法仍有许多有待进一步研究的方向。例如：理论研究方面，算法的收敛性分析以及收敛速度的估计；算法的全局搜索性能和算法不可避免的会陷入局部最优方面，可以考虑利用QPSO算法易与其他算法和策略融合的特性，汲取其他方法的优点进一步改善算法的性能；应用方面，仍需进一步的拓宽QPSO算法在各个领域的应用。

2.3 量子人工鱼群算法

量子人工鱼群算法（QAFSA）最初由唐涛[18]在2008年提出，将量子行为引入了人工鱼群算法，使量子算法强大的全局搜索能力和人工鱼群算法的局部搜索能力相结合。在一片水域中，鱼群最密集的地方一般就是附近营养物质最充沛的地方，人工鱼群算法模拟鱼群觅食、聚群、追尾等行为，找到营养物质最丰富的全局最优点。而QAFSA则采用量子编码表示个体的位置，量子计算特有的叠加和坍塌能带来更丰富的种群，量子旋转门利用当前最优个体的信息对鱼群进行更新，并引入量子变异、灾变等操作以缓解早熟等现象。结果证明，QAFSA在求解优化问题上有较好的性能，在聚类挖掘、信号检测、动态路径诱导等方面[48]得到了广泛的应用。

2.3.1 研究现状及应用

相比于前两种算法，目前国外对QAFSA的研究工作开展的较少，不过国内方面为了适应不同的优化问题，研究人员提出了各种改进的QAFSA模型，并以此引出了不少工程应用。王林川等[49]针对输电网络网架的优化规划建立数学模型，利用鱼群算法强大的局部搜索能力与量子算法混合，构造出探索和挖掘比较平衡的QAFSA对输电网规划问题求解，每次生成新个体便进行约束条件校验和剔除，在24节点系统上的实验结果表明该算法的可行性和有效性。张锴[50]对鱼群的视野和步长进行自适应改进，在算法运行的不同阶段动态的决定鱼群个体的视野和步长，提高算法的收敛速度和精度，同时设计了反馈-吞食行为用以去除鱼群中对算法执行贡献微小的个体，使得每次迭代更为高效，最终将算法应用于求解动态路径诱导问题，证明其可行有效。行鸿彦等[51]将变异操作引入量子人工鱼群算法，每次迭代后选出适应度较小的个体按照变异概率实现个体位置的随机跳动，提出了一种基于QGAFSA的随机共振微弱信号检测方法，将随机共振问题转化为多参数同步寻优问题，利用QGAFSA进行寻优，实现微弱信号的增强。李根[52]提出了一种基于量子人工鱼群的半监督模糊核聚类算法，用于解决基于传统模糊C均值聚类的网络入侵检测模型分类效果不佳等问题，适用于并行执行架构。对改进QAFSA算法的总结见表5。

表5 改进量子人工鱼群算法的优缺点和应用Table 5 Advantages and disadvantages of improved quantum artificial fish swarm algorithm and its applications

2.3.2 QAFSA总结及其局限性

目前针对量子人工鱼群算法的改进做出的研究仍然较少，与其他量子群智能优化算法相似，关于它的改进也主要集中在加快收敛速度、提高收敛精度以及防止陷入局部最优等问题上。量子人工鱼群算法具有一个显著的缺点就是当鱼群中个体数量较少时，无法体现其优势，鱼群的增大可以提高搜索速度，但同时也会加大存储开销，影响算法运行效果。基于以上问题，现有的文章多是在视野和步长的调整、鱼群行为的增加与优化等方面进行研究。相比于对算法的改进，其在应用层面的发展更为显著。

2.4 量子蜂群优化算法

量子蜂群优化（QBCO）算法最早是由Gao等[53]在2011年提出的，将Karaboga和Basturk[7]提出的人工蜂群算法（ABC）与量子计算相结合。自然界中，蜂群中的蜜蜂通过摇摆舞来传递蜜源的方向和距离等详细信息，借由这种群体之间的信息交换，蜂群能够找到附近的优质蜜源。ABC算法便是模拟蜂群这种觅食行为，QBCO算法则是在这种觅食机制的基础上，使用量子信息对蜜源进行编码以增加最优解的个数，并通过量子旋转门实现算法过程中的蜜源更新。与其他的量子群智能优化算法相比，QBCO算法的显著优点在于每次迭代都会将全局搜索和局部搜索相结合，收敛速度快，鲁棒性强。目前，QBCO在聚类分析、图像处理以及多目标优化问题等方面得到了一定的应用。

2.4.1 研究现状及应用

邓斯凯和毛戈[54]针对配电网多目标优化重构问题，用QBCO算法和Pareto支配关系进行求解，并将算法应用到标准IEEE 33节点配电网和加入分布式电源的配电网进行重构测试，测试结果表明了该算法的可行性。Gao等[53]将提出的QBCO算法用于解决CDMA（code division multiple access）系统在脉冲噪声存在下的鲁棒多用户检测问题，实验结果表明，所设计的鲁棒检测器在误码率（BER）等方面均比以往的检测器有所提升。在提出QBCO算法三年后，Gao等[55]为了更有效地解决离散优化问题，又提出了一种基于膜激发的量子蜂群优化算法（membrane-inspired quantum bee colony optimization，MQBCO），将膜计算理论引入QBCO，每个基础膜内包含一定数量的个体，膜将其与环境隔开，但不同膜之间也有着其通信规则且不限制个体的运动，文章还证明了MQBCO的全局收敛性能和有效性，随后将该算法用于解决认知无线电系统的决策引擎问题。Huo等[56]提出了一种改进的布洛赫量子人工蜂群（improved Bloch quantum artificial bee colony，IBQABC）算法，采用量子Bloch球坐标对蜜源信息进行三维编码，扩展了全局最优解的数量，并对更新策略做出相应改变，动态调整旋转角度，提高算法收敛速度以及跳出停滞状态的能力，并实际用于解决多层次图像阈值分割的问题，取得了不错的效果。同时，还有侯国莲和弓林娟[57]将QBCO算法作为聚类算法的前提部分辨识，提高了聚类速度，并应用于智能发电运行控制系统发电机组建模中，表现出良好的通用性和适应性。高相铭等[58]为解决多峰MPPT控制问题，将混沌搜索机制引入量子蜂群算法以选择最优SVR参数，提出了混沌量子蜂群算法CQABC，利用混沌搜索的特性将陷入局部最优的个体通过Logistic映射迭代产生混沌序列，提取序列中最优位置，使得算法能够继续有效运转。对改进QBCO算法的总结见表6。

表6 改进量子人工蜂群算法的优缺点和应用Table 6 Advantages and disadvantages of improved quantum bee colony algorithms and its applications

2.4.2 QBCO算法总结及其局限性

量子人工蜂群算法引入量子计算的概念，在一定程度上提高了蜂群算法的多样性和计算能力，但仍未能取得足够满意的效果。主要因为未充分利用量子编码的特性，以及量子蜂群更新过程的不稳定性。根本原因则在于对算法理论的研究和推导无法支撑起应用，而这也是量子群智能优化算法的通病，是所有这类算法未来研究的一个重要方向。目前针对该算法的改进也相对较少，多是将其作为其他方法的寻优部分来解决实际问题，研究者应更好的利用其在高维空间表现良好的优势对算法做出针对性改进，增强蜂群更新过程的稳定性，提升算法的寻优性能。

2.5 量子布谷鸟搜索算法

量子布谷鸟搜索算法（QCSA）是Layeb[20]提出的一种较新的量子群智能优化算法，已经应用于很多优化以及工程问题。QCSA的前身是布谷鸟搜索算法（CSA），CSA的灵感来源于一些布谷鸟在宿主鸟类的巢内产卵并由宿主鸟帮助孵化的自然现象。在自然界中，部分布谷鸟已经可以产出模仿一些鸟类宿主蛋的颜色和图案的蛋，大大减少产出的蛋被抛弃的几率。在CSA中，巢中的每一个蛋便代表着问题的一种解决方案，一个布谷鸟蛋则代表一种新的解决方案，其算法思想就是用新的、更好的布谷鸟蛋取代巢中不那么好的蛋[59]。最简单的情况就是每个巢只有一个蛋，扩展开来就是每个巢中的多个蛋代表一组解。

在QCSA中，设置完种群大小、迭代次数等基本参数后，首先要对宿主鸟巢进行量子编码产生初始解，再利用CSA中的莱维飞行搜索机制更新鸟巢的位置，并使用量子旋转门对发现的劣质鸟巢进行二次更新，最后采用局部邻域搜索算法对全局最优解进行优化[60]。

2.5.1 研究现状及应用

原始的QCSA已经被修改或者与其他算法进行混合，以解决不同的优化问题。一些涉及不同领域的复杂优化问题已经通过使用原始QCSA或者其变体得到了解决。Kartous等[59]基于全局/局部混合算法的随机渐进对齐方法来构造初始种群，提出了一种新的QCSA以解决生物信息学领域中主要问题之一的多序列比对（multiple sequence alignment，MSA）问题。杜传报等[61]则结合膜结构和QCSA，提出了膜量子布谷鸟搜索算法以解决无线双通道Ad Hoc网络中频谱资源分配优化的问题，算法使用量子信息编码鸟巢表示问题的潜在解，通过布谷鸟寻窝产卵的演化方法在基础膜中寻求单目标最优解，通过膜间信息共享和非支配解等级排序在Pareto前端解中求出多目标最优解。张东寅等[62]在原始的QCSA每次迭代的优化值附近引入了混沌局部搜索，生成混沌序列并借此在最优鸟巢附近随机生成一个新鸟巢，提出了一种融入量子计算和混沌局部搜索策略的改进布谷鸟算法，并针对IEEE 118节点系统的最优潮流计算问题进行仿真计算，得到了一种新的求解方法。刘志刚等[63]在QCSA中引入量化正交交叉策略，对发现个体和量子Pauli-Z门变异个体实施量化正交交叉操作，在正交区域中实施局部精细搜索，并应用到泥页岩多矿物组分反演问题中，反演精度有显著提升。Boushaki等[64]提出了一种新的用于数据聚类的量子混沌布谷鸟搜索（QCCS）算法，利用非齐次更新来扩展CS能力，同时采用混沌映射代替初始阶段的随机性，提高收敛速度。试验结果表明，提出的QCCS算法在内外聚类质量方面均明显优于标准布谷鸟搜索算法等8个已知算法。对改进QBCO算法的总结见表7。

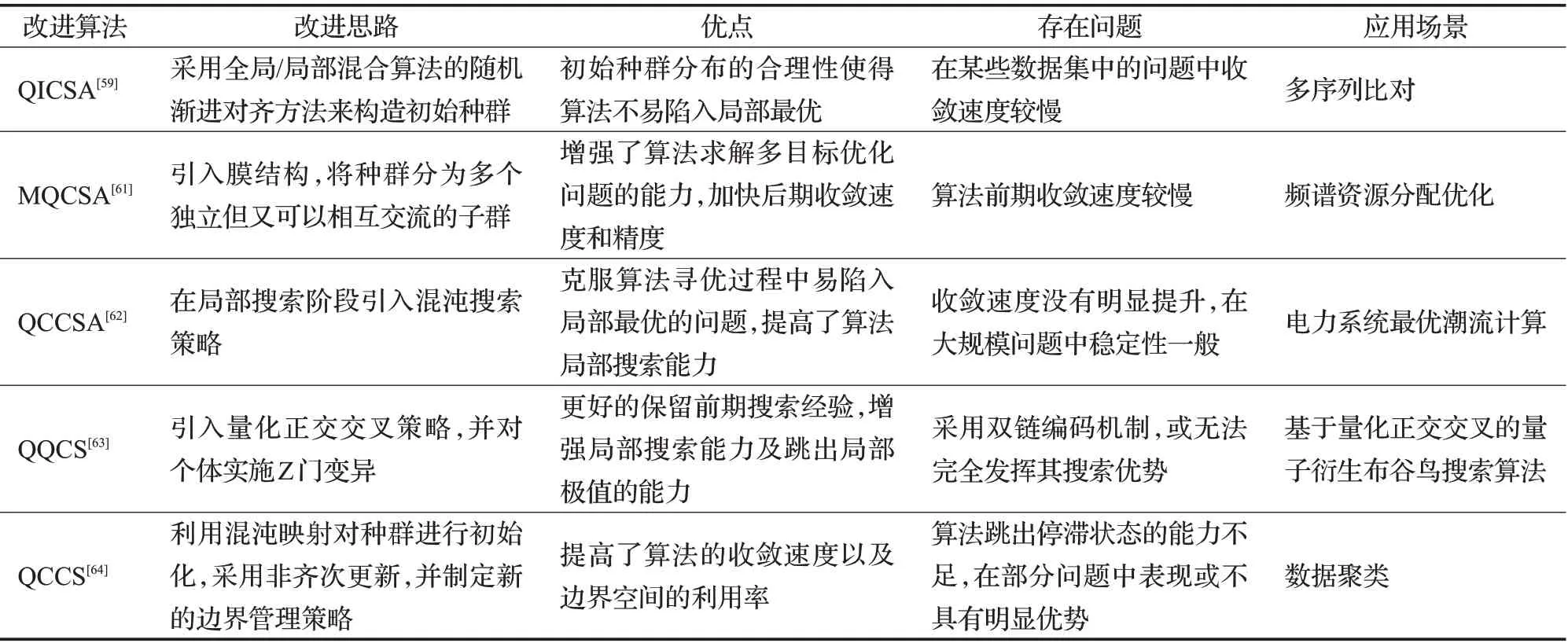
表7 改进量子布谷鸟搜索算法的优缺点和应用Table 7 Advantages and disadvantages of improved quantum cuckoo search algorithms and its applications

2.5.2 QCSA总结及其局限性

量子布谷鸟搜索算法自提出起受到了许多研究者的关注，对其进行的研究也相对较多。它的主要优势在于模型简单、参数较少、通用性强，但是它也存在收敛速度较慢、易陷入局部最优等问题。随着研究的不断深入，研究者对以上问题都提出了不同的解决方案和改进思路，目前QCSA及其改进算法在实际应用中的表现良好，进一步优化则可着眼于改进种群的编码方式、在搜索阶段引入新的策略和思想形成混合算法等方面。

2.6 新型量子群智能优化算法

近十年来，由于量子计算的发展以及群智能优化算法理论的不断进步，一些新颖的量子群智能优化算法被不断提出，主要包括量子混合蛙跳算法、量子萤火虫算法以及量子蝙蝠算法等，下面也将分别简要的对它们做出一些介绍。

2.6.1 量子混合蛙跳算法

量子混合蛙跳算法（QSFLA）2011年由孙冲[21]提出，经典的混合蛙跳算法是模拟自然界中青蛙之间在觅食时的信息交流，而QSFLA则是在此基础上采用量子信息对青蛙个体进行编码，并用量子旋转门进行种群的更新操作。相比经典的混合蛙跳算法，QSFLA不仅在寻优能力以及优化效率上有显著提升，并且还继承了经典混合蛙跳算法参数较少、易于实现等优点，缺点则是收敛速度相对来说依旧较慢，同时在面对部分问题时求解易陷入局部最优。

张强等[65]将QSFLA应用于神经网络的优化中，采用量子Bloch球面坐标对网络结构、网络参数和展开项数进行编码，沿球面两点间的劣弧进行更新操作，并在抽油机故障诊断和网络流量预测上进行了实验，取得不错效果。陈光宇等[66]采用QSFLA解决含DG的配电网无功优化，将每个可行解（即蛙群中的青蛙）编码为Bloch球上一点，通过量子旋转门对蛙群进行更新，并且利用Hadamard门对个体变异以避免早熟收敛，在IEEE 33节点系统上进行仿真实验，证明了算法的快速和有效性。Wang等[67]提出了一种新的量子启发蛙跳算法（NQSFLA）用于解决水下声纳图像检测问题，算法采用了类内差分和类间差分相结合的适应度函数来更准确地评价蛙的位置，并采用了一种新的进化更新策略将局部搜索分为两步，先利用相位角编码最差青蛙个体，亚群中其他个体则正常进化，以此来提高搜索过程中的搜索能力。为了避免QSFLA算法的缺点，他们还提出了一种带有空间信息模型的模糊隶属度矩阵，用于去除孤立区域。

2.6.2 量子萤火虫算法

量子萤火虫算法（QFA）2014年由张剑飞等[22]提出，经典的萤火虫算法灵感来源于萤火虫的显著特征：闪烁的光。在自然界中，这些光是用来吸引伙伴以及警告捕食者，当两只萤火虫之间的距离增加时，光的强度也会降低。萤火虫算法就是模拟这种发光机制，不断向更具吸引力的萤火虫个体移动。QFA则是在此基础上采用量子信息对萤火虫个体进行编码，扩展寻优空间，并采用量子旋转门对个体位置进行更新。

赵俊丽[68]针对QFA易早熟等缺点，提出了三种组合策略的量子萤火虫算法：自适应步长策略以解决算法在最优值附近震荡的问题；广义精英反向学习策略应对QFA对初始种群分布合理性的依赖；边界控制策略增加边界个体的随机性。采用最小交叉熵作为适应度函数，将三种改进后的QFA应用于图像分割研究，实验证明在MSSIM和PSNR方面都取得了显著提升。Shareef等[69]采用量子启发二进制萤火虫算法寻找最佳的网络重构，并将这种网络重构方法应用于提高配电系统的电能质量和可靠性。齐学梅等[70]设计了一种新的局部邻域搜索方法，与QFA相结合，每次迭代时只搜索部分邻域，极大加快了算法迭代的速度，并将该算法应用于无等待流水调度，验证了其优越性。Tao等[71]将遗传算法中交叉和突变的概念引入QFA，通过交换部分量子位实现交叉、改变个体的部分量子位实现突变，以此获取新的信息来保持种群的多样性。

2.6.3 量子蝙蝠算法

量子蝙蝠算法（QBA）2013年由李枝勇[23]提出，经典的蝙蝠算法基于自然界中微型蝙蝠的回声定位特性。在经典算法中有如下规则：蝙蝠随机飞行，使用回声定位感知距离，根据与目标的距离调整波长，响度由最大值逐渐降低到一个最小的恒定值。在QBA中，采用量子信息对蝙蝠位置进行编码，蝙蝠位置的更新则通过量子旋转门改变量子位的相位来实现。其优点在于全局和局部搜索能力较为平均，运算速度快，但是其求解精度低以及易陷入局部最优的缺点也同样明显。

Huo等[72]通过定义服务空间算子并用量子理论修改蝙蝠算法的定位生成方法，将QBA应用到服务组合问题中，仿真实验结果表明该算法具有较好的性能。Huang等[73]提出了一种具有平均最佳位置定向的高斯量子蝙蝠算法，该算法利用高斯分布生成随机数序列，应用高斯分布而不是均匀分布来生成随机系数提高其避免过早收敛的性能，用于求解数值函数优化问题。实验表明，在大多数情况下，该算法能够提供更好的搜索性能。Li等[74]提出了一种混沌云量子蝙蝠算法，该算法利用X条件云发生器提高具有较好适应度个体的收敛速度，在一定迭代次数后对个体进行排序，并将3Dcat映射混沌干扰机制应用在适应度较差的个体上，提高种群多样性。周志垚等[75]在QBA的基础上引入自然选择，同时针对算法的频率引入优化因子，前期更多的进行全局搜索，后期则提高局部搜索能力。并将该算法应用于化工过程的动态优化问题中，取得了较好的效果。

新型算法改进的优点和应用对比见表8。

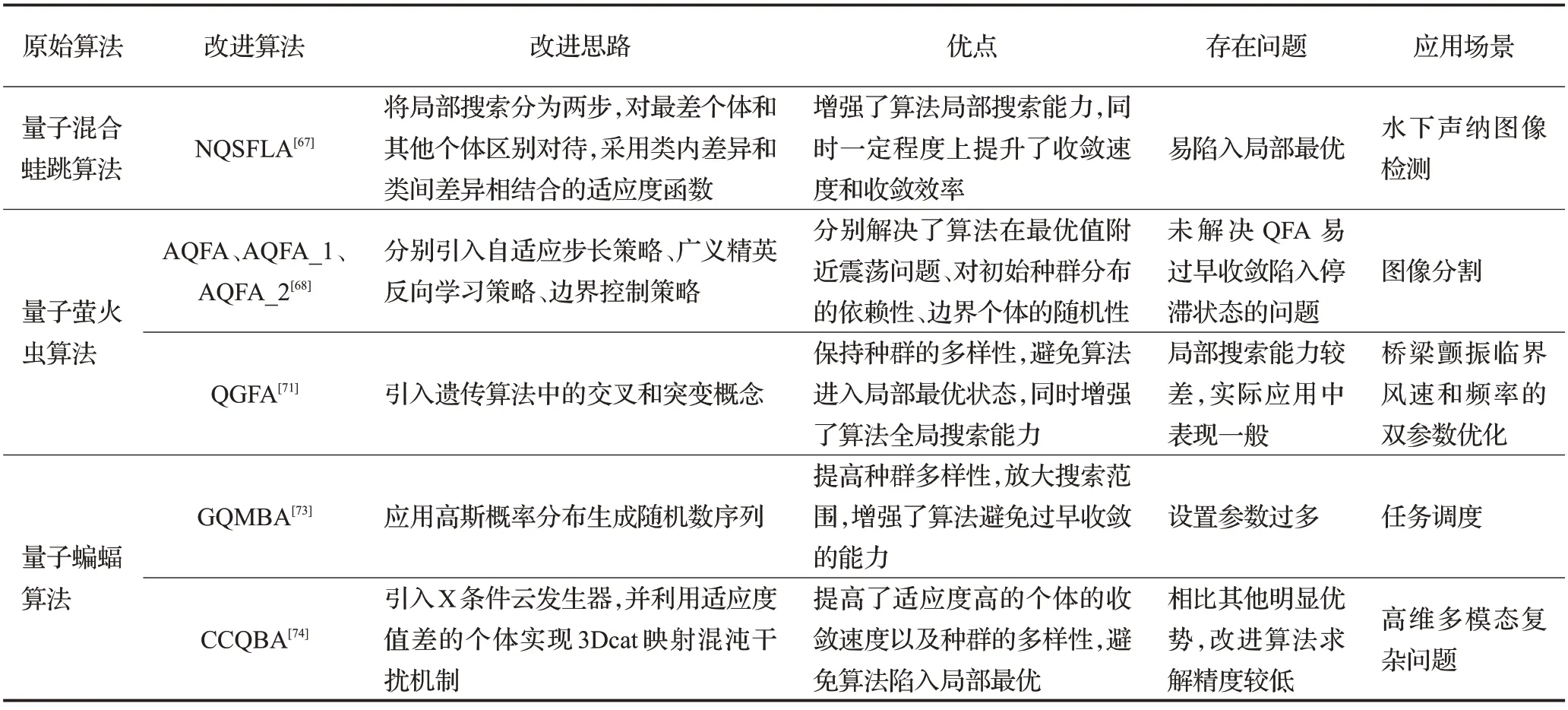
表8 新型算法改进的优缺点和应用Table 8 Advantages and disadvantages of new algorithms improvement and its applications

3 主要面临的问题

量子群智能优化算法的发展迅速，对它的研究多是在应用层面的改进，主要集中在改进种群编码方式、与其他策略和思想融合形成混合算法并应用于具体问题等。但是时至今日，量子群智能优化算法的理论基础依旧不够完善。而理论分析对于我们深入理解算法的机理有着重要作用，对算法进行收敛性和稳定性分析有助于其进一步的发展。并且，从理论分析角度对算法的性能进行评测也更有说服力和学术价值。

对于一个优化算法来说，对其进行收敛性分析是十分必要的。目前的研究状况表明，建立一个可以对量子群智能优化算法进行理论分析的一般框架的数学模型十分困难，已经提出并实现的这类算法大多没有进行系统的收敛证明，这也限制了它们在现实优化问题上的进一步应用。同时，当一种算法被用于解决一个或一类新问题时，对算法的进行适应性改进以及选择最优的参数设置十分重要。但是目前的参数设置都只是经验性的，或者说是针对某一实验大量测试后选择的，那么如何从理论角度给出算法最优参数设置的选择依据，也是需要进一步研究的问题。

目前在不同量子群智能优化算法的优缺点方面的对比不够清晰，多是对几个算法进行尝试性实验，在理论层面不具有说服力，这直接导致了使用者在应用这类算法时的选择困难。因此，需要建立一个标准的复杂性分析以及其他性能指标评估与分析的模型，更清晰的列出不同算法的优缺点，既有助于研究者更针对性的对算法性能做出改进与提升，同时也可以减轻使用者的选择负担。

除理论分析方面需要寻求突破以外，由于通用量子计算机的落地还比较遥远，在目前已有文献中的算法应用实现过程都是在经典计算机模拟并简化实现的，模拟实现相比现有量子计算原型机的复杂情况来说过于理想化，效果或有提升但并不显著。如果想探索算法短期内在现有机器上的实现，可以结合具体机器和问题在经典计算机上进行更符合实际的研究，如添加噪声、半衰期等概念。但要想更好地发挥量子群智能优化算法在实际应用中的性能，未来还需要依托于通用量子计算机的实现。

4 结束语

本文回顾了量子群智能优化算法的由来和发展史，对当前典型的量子群智能优化算法的原理、实现过程、改进以及在具体优化问题上的应用进行了介绍，讨论了目前面临的主要问题与挑战，并对需要重点研究的方向和方法进行了叙述。可以预见，未来量子群智能优化算法在系统的应用于现实优化问题时，将继续并更充分地显示出其突出和不可替代的优势。