基于弹簧模型的重要节点排序算法

孟昱煜，王 霄，闫光辉，罗 浩，杨 波，张 磊，王 琼

1.兰州交通大学 电子与信息工程学院，兰州 730070

2.国网甘肃省电力公司信息通信公司，兰州 730070

随着信息技术的发展，复杂网络（complex networks）已经深入到人类社会的各个方面[1]。作为刻画复杂系统相互作用的重要工具[2]，复杂网络可以描述自然界中的大量复杂系统，如生物领域的食物链网络[3]、新陈代谢网络[4]；信息领域的www网络[5]、论文引用网络[6]等。复杂网络的节点在结构和功能上承担着不同作用[7]，其中重要节点是指相比复杂网络的其他节点而言能够在更大程度上影响网络的结构与功能的一些特殊节点，重要节点排序对于挖掘网络的重要节点意义重大。重要节点数量很少，但其影响却可以快速地波及到网络中大部分节点[8]。如微博中最有影响力的几个用户所发的微博很快就能传遍整个网络[9]；仅仅1%的公司却控制着40%的全球经济[10]；再如2019年12月在湖北省武汉市爆发的新型冠状病毒通过少数感染人群在较短时间将疫情蔓延至全国[11]，如果能够通过重要节点排序算法对超级传播者[12]（即重要节点）早发现早隔离，就能够尽早控制住疫情。

在网络科学研究中，设计有效的重要节点排序算法，有着很强的理论研究和实践意义[13]。学者们在重要节点排序上提出了很多指标与算法[14]，大致可分为4类：（1）基于节点近邻的排序算法。其中，度中心性DC（degree centrality）[15]仅考察节点的直接邻居数目；H指数（H-index）[16]定义为节点至少有h个邻居的度不小于h的最大h值；K-壳分解法（K-shell）[17]认为节点的重要性取决于节点在网络中的位置，通过将外围节点层层剥去，挖掘出具有较高重要性的内层节点。度数（归一化后为度中心性DC）、H指数H-index和核数或者壳数Kshell是H算子作用下的初始态、中间态和稳态[18]，它们对网络节点重要性的划分是粗粒化的。这类算法最简单直观，缺点是仅仅考虑了网络节点的邻居信息，忽略了路径对网络中的节点重要性的影响。（2）基于路径的排序算法。其中，介数中心性BC（betweenness centrality）[15]认为网络中所有节点对的最短路径中，经过一个节点的最短路径数越多，这个节点就越重要[8]；接近中心性CC（closeness centrality）[15]认为一个节点与网络中其他节点的平均距离越小，该节点的接近中心性就越大[8]。这类算法的缺点是仅仅考虑了网络路径的信息，忽略了节点近邻的影响，且时间复杂度较高。（3）基于迭代优化的排序算法。其中，特征向量中心性EC（eigenvector centrality）[19]认为一个节点的重要性既取决于其邻居节点的数量（即该节点的度），也取决于每个邻居节点的重要性；PageRank[20]是网页排序领域中的著名算法，它认为万维网中一个页面的重要性取决于指向它的其他页面的数量和质量，如果一个页面被很多高质量页面指向，则这个页面的质量也高[8]，其主要应用于有向网络。（4）基于节点移除和收缩的排序算法。其中，节点删除的生成树法通过计算节点删除后网络的生成树的减少比例来反映节点的重要性。这类算法研究节点移除或者收缩后网络的结构与功能的变化，是一种动态的方法，缺点是计算复杂度较高，与上述3类方法相比，更像是一种对于重要节点排序算法的评价指标。

如果两个社团之间仅通过一个节点连接，那么，虽然这个节点只有很小的度，但是却具有极大的重要性，因为它具有很大的介数，随着这样的节点的移除，网络的连通性将会急剧降低。在真实网络中，很多的节点往往只与一个度很大的节点直接连接，当这个度大的节点处在网络边缘时，虽然它的介数会很小，但是它却很重要，因为它具有很大的节点度，随着这样的节点的移除，网络中将会产生很多孤立节点，网络的最大连通分支的节点数目也会快速下降。当用度中心性DC来评价节点重要性时，不能很好地识别上述度小而介数大的重要节点；当用介数中心性BC来评价节点重要性时，对上述度大而介数小的重要节点的识别能力较弱；当用接近中心性CC来评价节点重要性时，由于和介数中心性BC一样也是一种基于路径的重要节点排序算法，同样会忽略节点度对节点重要性的影响，甚至对于上述那种处在网络边缘的度大的节点，接近中心性CC认为它的重要性甚至不如去除后对网络结构与功能几乎没有太大影响的处在网络较中心位置的节点；当用特征向量中心性EC评价节点重要性时，由于其认为一个节点的重要性既取决于其邻居节点的数量，也取决于每个邻居节点的重要性，说明节点对其邻居有很强的依赖性，当其邻居从网络中移除后，这种节点的后续移除往往对网络的结构与功能不会有太大影响，因为它的重要性依赖于其邻居的重要性，而当其邻居节点移除后，它的重要性也会快速衰减。

尽管专家学者在重要节点排序领域开展了大量的研究工作，也取得了丰硕的成果，但基于节点近邻的算法往往忽略了路径对节点重要性的影响，基于路径的算法也不能对节点近邻进行充分考虑，基于特征向量的排序算法太过依赖于其邻居节点的重要性，算法在重要节点排序精度方面仍然存在提升之处。Li等人[21]提出的GM算法和其局部算法LGM充分结合了网络中节点近邻和路径的信息，在引力公式的启发下，通过把节点的度看作物体的质量，把节点间的最短路径长度看作物体间的距离，深化了引力模型的内涵。肯德尔等级相关系数τ[22]可以用来衡量重要节点排序算法赋予给节点的重要性值序列与SIR传播模型[23]中的对应节点的影响力序列之间的一致性强度，将其作为评价指标，显示出了这两种算法的优势。在GM算法和LGM算法的基础上，考虑到节点间影响力随着节点度数的增大而增大，随着节点间最短路径长度的增大而减小，受到弹簧模型的启发，进一步融合网络节点近邻和路径信息，并结合网络直径，提出SM算法和其局部算法LSM。将其与GM、LGM以及网络对于节点移除的鲁棒性和脆弱性的2种表现最好的经典算法DC和BC进行比较，在2种合成网络和4种真实网络的实验结果表明SM算法和LSM算法对于网络中重要节点排序具有更高的准确性。特别地，在SIR传播模型下，将SM算法得到的排名靠前的重要节点作为一个感染节点集合，在Power网络上的实验结果显示该感染集相较于其他算法得到的感染集能以更快的速度感染网络中的其他易感节点，稳态时也具有更大的感染范围，证明SM算法对于网络中重要节点排序具有更高的合理性和有效性。

1 重要节点排序算法

1.1 GM算法和LGM算法

GM算法和LGM算法用节点引力来描述节点的重要性，也就是影响力。其中，GM算法充分结合网络中节点近邻信息和节点间的路径信息，在引力公式的启发下，通过把网络中节点的度看作物体质量，把节点间的最短路径长度看作物体之间的距离，计算出各节点之间的引力，遍历求和得到每个节点的总引力，对其从大到小排序得到一个重要节点排序结果。

定义1G i定义为网络中节点i的引力，其计算公式为：

其中，k i代表节点i的度，d ij代表节点i和节点j之间的最短路径长度，j遍历网络中i以外的所有其他节点。令节点自身之间的引力为0。

定义2为了降低GM算法的计算复杂度，通过只考虑截断半径r g以内的引力，提出了LGM算法，G r i定义为网络节点i的局部引力，其计算公式为：

在14个数据集里，与经典算法相比，GM算法和LGM算法赋予给节点的重要性值（引力）序列与SIR模型中的对应节点的影响力序列之间的肯德尔等级相关系数τ取得了较大值，甚至在某些数据集里，LGM算法取得了最大的τ，体现了算法的优越性[21]。观察公式（1）和（2），对于网络中的节点i，如果它有较小的节点度k i，那么很难通过计算得到较大的引力Gi和局部引力G r i。由于引力和局部引力的计算公式中的分母都是平方项，节点与其低阶邻居之间具有较小的最短路径长度，因此，G i和G r i的值主要由低阶邻居的节点度决定。节点引力（包含局部引力）的计算公式决定了GM算法和LGM算法对度小的重要节点识别能力较弱，并且节点的引力依赖于近邻节点的度数，用网络的鲁棒性和脆弱性指标评价重要节点排序算法时，度大的节点和其近邻节点往往具有较大的节点引力，当度大的节点从网络中移除后，一般来说，其引力较大的近邻节点的后续移除并不能在很大程度上影响网络的结构与功能，说明算法在重要节点排序精度方面仍然存在提升之处。为进一步提升算法在网络的鲁棒性和脆弱性方面的表现，在弹簧模型的启发下，提出SM算法和LSM算法。

1.2 SM算法和LSM算法

将以胡克定律[24]为基础的弹簧模型引入到复杂网络的重要节点排序领域，提出基于弹簧模型的重要节点排序算法SM和其局部算法LSM。

定义3在弹簧模型中，F定义为弹簧的弹力，其计算公式为：

公式（3）是弹簧模型的表达式。其中，F代表弹簧的弹力，k代表弹簧的劲度系数，x代表弹簧的形变量。考虑到弹簧的弹力随着弹簧的劲度系数和形变量的增大而增大，类似地，复杂网络中两节点之间的影响力随着节点邻居数目（度数）的增大而增大，随着节点间最短路径长度的增大而减小，也就是说随着网络直径d与网络节点间最短路径长度的差值的增大而增大，将网络中的节点i和节点j以及它们之间的最短路径看作一个原长为网络直径d的弹簧，基于弹簧模型，并受GM算法的引力计算公式的启发，把节点i和节点j的度的乘积k i k j视作弹簧的劲度系数k，把网络直径d与两节点间的最短路径长度d ij的差值d-d ij视作弹簧的形变量，将两节点之间的弹力视作弹簧的弹力F，并将其视为标量，只考虑大小，不考虑方向，即可计算得到网络中各节点与其他所有节点间的总弹力，也就是各节点的重要性值。

定义4S ij定义为节点i和节点j之间的弹力，其计算公式为：

SM算法和LSM算法用节点弹力来描述节点的重要性，或者说影响力。其中，SM算法进一步考虑网络中节点近邻信息和节点间的路径信息，并结合了网络直径d。为提高重要节点排序精度，基于弹簧模型，借助胡克定律，计算各节点之间的弹力，遍历求和得到每个节点的总弹力，对其从大到小排序得到一个重要节点排序结果。SM算法与GM算法的最大不同是：SM算法考虑了网络直径d对节点重要性的影响。

定义5Si定义为网络中节点i的弹力，其计算公式为：

令节点自身之间的弹力为0。公式（5）表明：（1）有较多邻居数目和较小最短路径长度的两节点间具有较大的影响力，符合直观判断。（2）节点的邻居数目越多，与网络中其他节点的最短路径长度越小，节点的影响力越大，即越重要。（3）两节点间的最短路径长度为d时，节点间影响力为0。（4）网络直径反映出网络中具有最大最短路径长度的两节点间建立联系的困难程度，且是一种网络尺寸度量。有相同k i、k j和d ij值的两节点i和j处在不同网络直径的网络时，它们之间的影响力是不同的，SM算法认为处在较大网络直径的网络时两节点间的影响力较大。下面给出SM算法的伪码描述：

算法1 SM重要节点排序算法

Input：undirected networkG=(V,E)

Output：the result of node ranking

1.begin

2. calculate the degreek′of each node，the shortest path lengthd′between nodes and the network diameterd

3. for nodeiinVdo

4. calculateSiaccording to formula（5）

5. end

6. rankSifrom large to small to get the result of node ranking

7.end

下面分析算法的时间复杂度。对于给定的复杂网络G，网络包含n个节点和m条边，SM算法的时间耗费主要在于计算所有节点对之间的最短路径长度，通过Johnson算法[25]计算全源最短路径的时间复杂度为O(n2lbn+nm)，因此SM算法的时间复杂度为O(n2lbn+nm)。

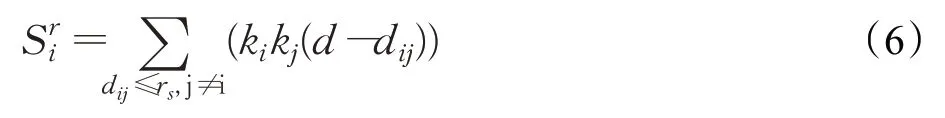
定义6通过只考虑截断半径r s以内的弹力，提出LSM算法以降低SM算法的计算复杂度，S ri定义为网络节点i的局部弹力，其计算公式为：将算法1中的第4步改为通过公式（6）计算节点i的局部弹力S ri，即可得到LSM算法的伪码描述。同样的，LSM算法的时间复杂度也是O(n2lbn+nm)。表1显示了基于弹簧模型的重要节点排序算法SM和其局部算法LSM、基于引力模型的重要节点排序算法GM和其局部算法LGM、度中心性DC、介数中心性BC这6种算法的时间复杂度。可以看到除度中心性DC外的其他5种算法具有相同的时间复杂度，均为O(n2lbn+nm)。

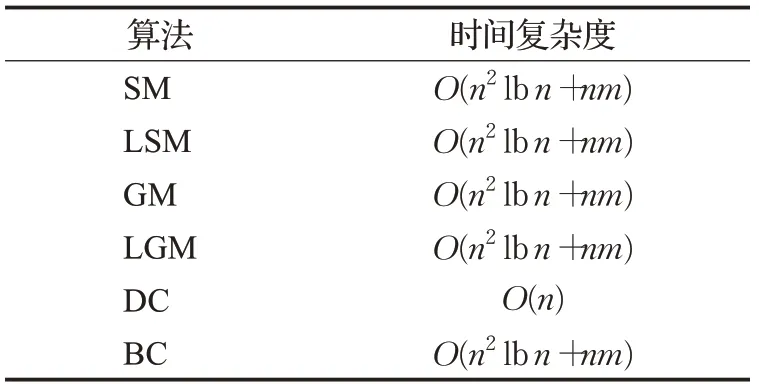
表1 6种算法的时间复杂度Table 1 Time complexity of six algorithms

GM算法和LGM算法的计算公式决定了度大的节点和其邻居节点会具有较大的重要性值（引力值），观察公式（5）和公式（6），由于节点弹力的计算公式中k i、k j和d-d ij是一次项相乘的形式（对于选定网络，网络直径d为定值），与GM算法和LGM算法的节点引力的计算公式相比，增强了最短路径对节点重要性的影响，也就是提高了介数对于节点重要性的作用。介数大的节点有更多的最短路径通过，从概率上来看，这类节点往往与网络中的其他节点有更小的最短路径长度，因此它会有较大的节点弹力。对于一些度小而介数大的节点，其弹力值仍然可能很大，在这点上，SM算法和LSM算法与GM和LGM算法有很大的不同。基于节点近邻的算法（如度中心性DC）只需知道网络中节点的邻居信息；基于路径信息的算法（如介数中心性BC）只需知道节点间的路径信息；基于引力模型的GM算法和LGM算法虽然考虑了节点的近邻信息和路径信息，但以网络对于节点移除的鲁棒性和脆弱性指标评价排序算法时，由于节点重要性过于依赖邻居节点的重要性，以至在重要节点排序精度方面仍然存在提升之处；基于弹簧模型的SM算法和LSM算法充分结合网络中节点近邻信息、路径信息以及网络统计特征中的直径信息，对网络的整体拓扑结构信息有充分把握，并增强了最短路径对节点重要性的影响，即削弱了节点对其邻居节点的重要性的影响，当度大的节点从网络中移除后，对其邻居节点的重要性不会有太大影响，也就是说不会在很大程度上削弱邻居节点移除对网络结构和功能的影响，维持了原网络重要节点排序的精度，表明SM算法和LSM算法能够对网络中的重要节点进行更准确的排序。

2 实验分析

2.1 数据集描述

为了客观评价算法的有效性和适用性，选取了2种经典的合成网络和4个公开的不同规模的真实网络数据集。BA无标度网络和WS小世界网络是复杂网络中最重要的2个网络模型，本文基于BA无标度网络模型和WS小世界网络模型构建了2种10 000个节点的人工合成网络：BA无标度网络（BA）和WS小世界网络（WS），并选取了4种真实网络：遗传疾病网络（Diseasome）[26]、蛋白质相互作用网络（Y2H）[27]、美国西部电力网络（Power）[28]、性社交网络（Sex）[29]，其网络参数如表2所示。

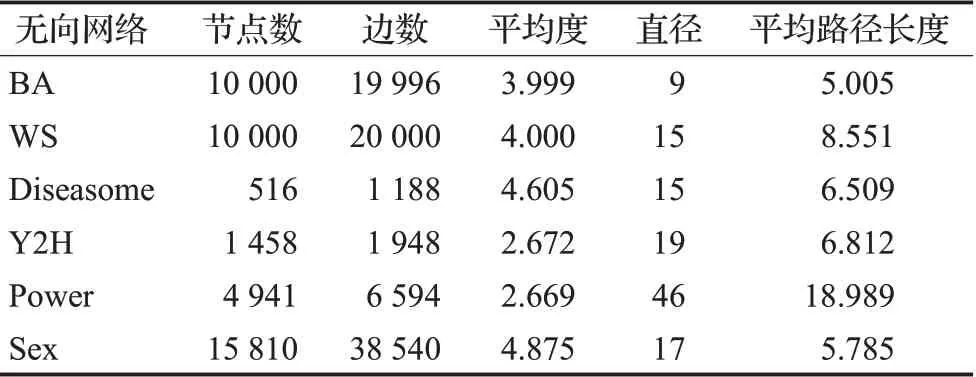
表2 6种无向网络的参数Table 2 Parameters of six undirected networks

2.2 网络的鲁棒性和脆弱性验证实验

网络的鲁棒性和脆弱性验证实验着重考察网络中一部分节点移除后网络结构和功能的变化，变化越大说明移除的节点越重要[8]。对于一个节点数为n、连边数为m的网络，用重要节点排序算法对网络中的所有节点进行重要性排序，得到一个重要节点排序序列，再按照重要性大小依次移除网络中的节点，直到网络的节点集和边集都为空集。其中，把移除i n比例的节点后的网络的最大连通分支的节点数目占网络初始节点数目n的比例记为σ(i/n)。

定义7R定义为网络对于节点移除的鲁棒性（robustness）[8]：

定义8V定义为网络对于节点移除的脆弱性（vulnerability）[8]：

V值越大代表节点移除方法越有效，即表示重要节点排序算法越好。以重要节点排序算法的节点序列作为节点移除序列，把i n和σ(i/n)分别作为横纵坐标，可在二维坐标作出算法的σ(i/n)值随i n的增大而减小最后趋于稳定值0的曲线图。在同一网络中，与其他重要节点排序算法相比，某种排序算法作出的曲线图，对于相同的i n，有较小σ(i/n)值，说明移除i n比例的节点后，剩余网络具有较小的最大连通分支节点数。由公式（7）和公式（8）可知，随着i n的变化，若某种重要节点排序算法都有最小的σ(i/n)值，即曲线的纵坐标离横轴最近，则这种算法有最小的R值和最大的V值，也就是说，算法在网络的鲁棒性和脆弱性指标的评价下表现得最好。

以网络的鲁棒性和脆弱性指标评价重要节点排序算法时，为了找到在此方面表现较好的经典算法，选取度中心性DC、介数中心性BC、接近中心性CC、H指数H-index和K-壳分解法（K-shell）这5种经典的重要节点排序算法，在上述6个数据集上进行网络的鲁棒性和脆弱性实验，如图1所示，其中条形图的高度代表V值的大小，图例中附有各种算法的V值。对上述5种排序算法得到的V值从大到小排序，可知DC和BC的V值在6个数据集中都分别居于第1和第2位。并且6种网络中的曲线图表明，DC和BC的σ(i/n)值随着i n的增大有较大的下降趋势，说明以这2种算法移除网络中的节点时，网络会变得极其脆弱。由此可知，度中心性DC和介数中心性BC是在这6个数据集表现得最好的2种经典算法。

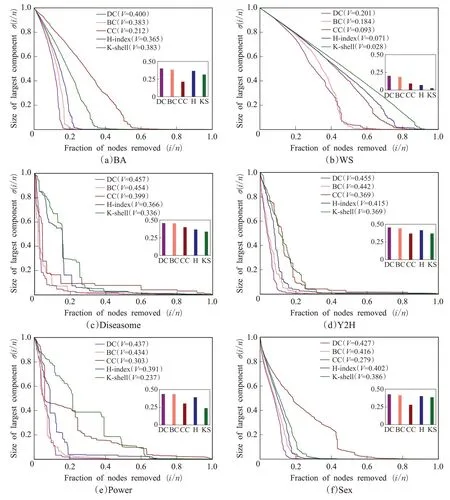
图1 经典算法在6种网络上的鲁棒性和脆弱性实验Fig.1 Experiments on robustness and vulnerability of classical algorithms on six networks

LSM算法和LGM算法存在最优截断半径（使LSM算法和LGM算法具有最大V值的最小截断半径）的选取问题。为了得到LSM算法和LGM算法在较小计算复杂度下的最优截断半径和，只考虑截断半径为10以内的情况，由于BA网络直径为9，所以其只考虑到9以内的截断半径，以截断半径r为横坐标，以V值为纵坐标，在6个数据集上对比LSM算法和LGM算法在不同截断半径r下的V值，作出V值随r增大而变化的折线图V-r，实验图如图2所示。设LSM和LGM的最优截断半径分别为和。对于BA网络，如图2（a）所示，6；对于图2（b）、图2（d）和图2（e）中的WS网络、Y2H网络和Power网络，10；对于Diseasome网络，如图2（c）所示，10，7；对于Sex网络，如图2（f）所示，7。在6种网络中，LSM在取得的V值均大于LGM在取得的V值，说明LSM算法在网络的鲁棒性和脆弱性上较LGM算法具有一定优势。为了使局部算法LSM和LGM具有更强的适用性，最优截断半径可以取成一个定值。当r s=r g=10时，实验结果显示LSM算法和LGM算法在除BA网络外的其他5种网络中的V值均可以取到最大值。对于BA网络这样的直径小于10的网络，把最优截断半径取成网络直径，此时，LSM算法和SM算法、LGM和GM算法完全等价。可以看到，在6种网络中，以上述这种方式选取最优截断半径时，LSM算法和LGM算法可以取得最大的V值，并且，LSM算法的V值总比LGM算法的V值大，体现了以网络鲁棒性和脆弱性指标评价排序算法时，LSM算法相较于LGM算法的优越性。

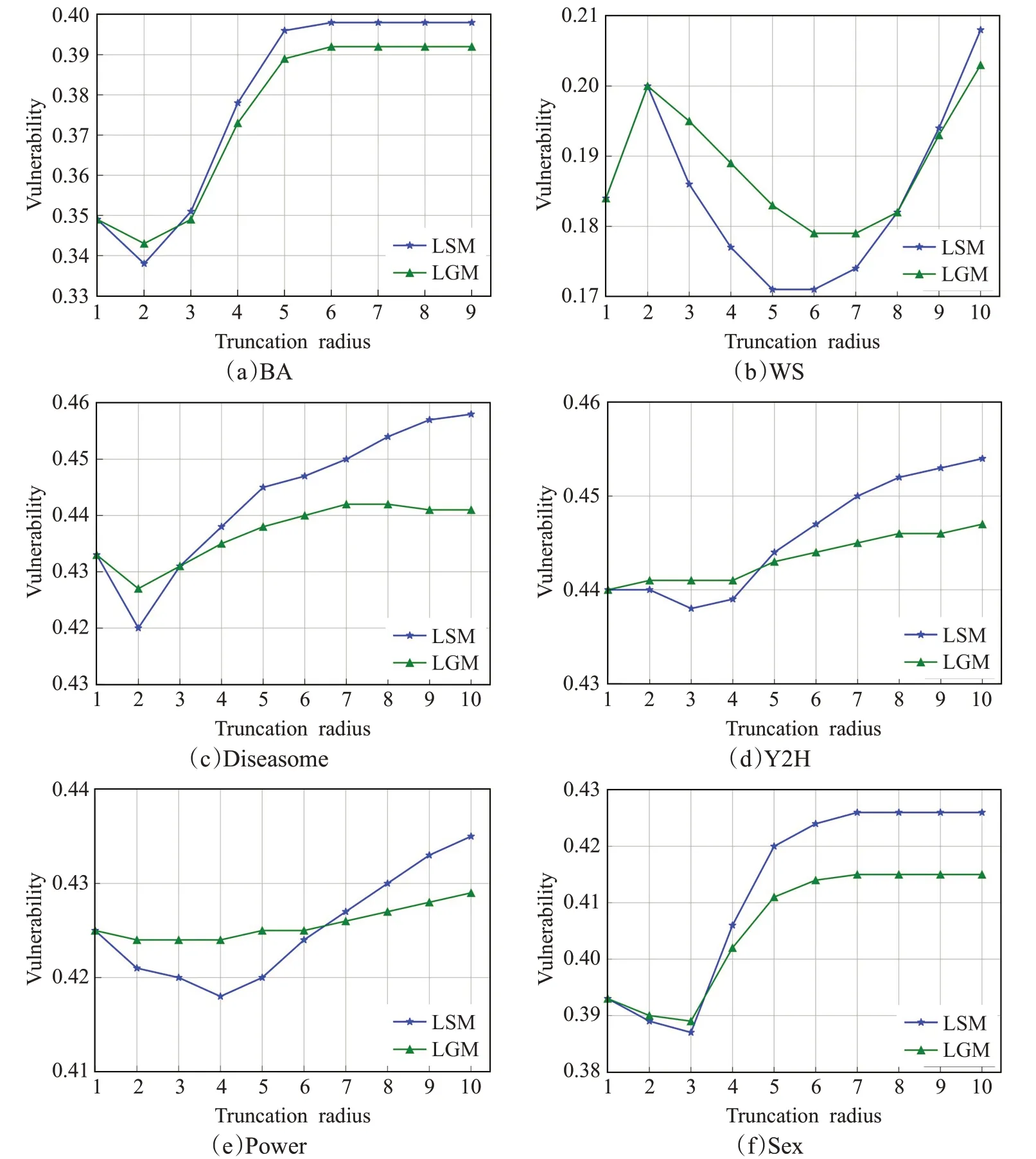
图2 LSM和LGM关于6种网络的V-r图Fig.2 V-r graphs of LSM and LGM on six networks

以上述方式选取在最优截断半径（网络直径大于或等于10的网络，最优截断半径取10；网络直径小于10的网络，最优截断半径取为网络直径）下的LSM算法和LGM算法，以及全局算法SM和GM，还有与其他3种算法相比，表现得最好的经典算法DC和BC这6种算法，在6种网络上对基于弹簧模型的重要节点排序算法SM和局部算法LSM进行网络的鲁棒性和脆弱性验证实验，实验结果如图3所示。设SM、LSM、GM、LGM、DC和BC的V值分别为VSM、VLSM、VGM、VLGM、VDC和VBC。对于BA网络和Sex网络，如图3（a）和图3（f）所示，VSM=VLSM＞VGM=VLGM，反映在曲线图中，SM和LSM的曲线基本重合，GM和LGM的曲线也几乎一致。在6种算法中，VSM和VLSM仅小于VDC，对应于曲线图中SM和LSM的σ(i/n)值随着i n的增大的下降趋势仅小于DC的σ(i/n)值的下降趋势。对于WS网络和Power网络，如图3（b）和图3（e）所示，VSM＞VLSM＞VGM＞VLGM，在6种算法中，VSM最大，VLSM在WS网络中仅小于VSM，VLSM在Power网络中仅小于VSM和VDC。对于Diseasome网络，如图3（c），VSM=VLSM＞VGM=VLGM，在6种算法中，VSM和VLSM的值最大。对于Y2H网络，如图3（d），VSM＞VLSM＞VGM=VLGM，在6种算法中，VSM与VDC相等，大于其他4种算法的V值，VLSM在Y2H网络中仅小于VSM和VDC。在6种网络中，VSM≥VLSM，VGM≥VLGM，说明以网络的鲁棒性和脆弱性评价重要节点排序算法时，全局算法一般会优于局部算法。6种网络的鲁棒性和脆弱性实验反映出SM算法和LSM算法不仅优于GM算法和LGM算法，甚至在某些网络（WS网络、Diseasome网络、Y2H网络、Power网络），SM算法的表现要比传统的重要节点排序算法好。反映出用网络的鲁棒性和脆弱性评价重要节点排序算法时，SM算法和LSM算法对于网络中重要节点排序具有更高的准确性。图3（a）和图3（b）分别是BA无标度网络中和WS小世界网络中的鲁棒性和脆弱性验证实验，相比WS小世界网络，6种算法在BA无标度网络中具有更大的脆弱性，说明以重要节点排序算法的排序结果来移除网络中的节点对BA网络的破坏程度更大，反映了BA无标度网络的少数节点具有极大的度、大部分节点具有极小的度的无标度特性导致的其对蓄意攻击（按重要性大小移除网络中的节点）表现出的极大的脆弱性。WS小世界网络中的较小的脆弱性反映了其高聚类的特性，高聚类说明节点的邻居之间互为邻居的概率很大，以排序算法的排序结果来移除网络中的节点时，网络的连通性不容易遭到破坏。图3（c）～（f）中的4种真实网络的实验结果与BA无标度网络的实验结果更接近，6种算法在这5种网络中都具有较大的脆弱性，且都在移除大约20%的节点后，网络的最大连通分支的节点数目就趋近于0（网络变得完全不连通），网络的拓扑结构遭到极大破坏，反映了真实网络类似于BA网络的无标度特性；不同于其他5种网络，图3（b）中的WS小世界网络在移除60%的节点后网络的最大连通分支的节点数目才趋近于0，反映了具有高聚类特性的WS小世界网络对蓄意攻击的表现出的较大的鲁棒性。

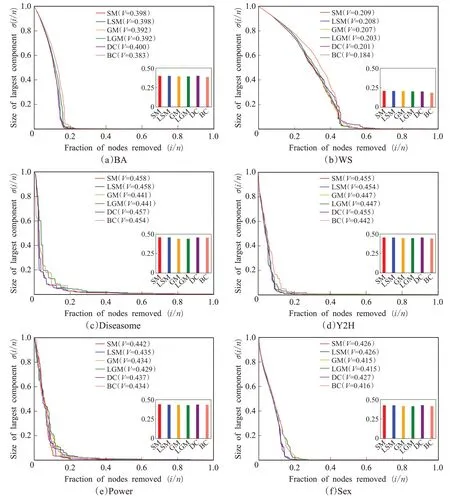
图3 SM和LSM在6种网络上的鲁棒性和脆弱性验证实验Fig.3 Experiments on robustness and vulnerability of SM and LSM on six networks

2.3 SIR传播模型验证实验

此类方法着重考察网络中节点对于信息的传播能力或者是病毒在网络中的扩散能力。SIR模型中，一个节点的传播能力被定义为该节点的平均传播范围，如果一个排序算法的结果使得网络流传播又快又广，则说明该重要节点排序算法优于其他算法[8]。

SIR模型认为网络中的节点有3种状态：易感态S（susceptible）、感染态I（infected）和免疫态R（recovered）。其中，对于每个时间步t，处于感染态I的节点可以感染其处于易感态S的邻居节点，感染概率设置为β，即它的每个处于S态的邻居都有概率β被感染为I态节点。另外，设置恢复概率为λ，即每个处于I态的节点都有概率λ恢复为不会传染也不会被感染的R态节点。设置网络中所有节点初始状态都为S，对于各种重要节点排序算法，选取其重要性排在前面的某些节点作为感染态节点I，在有限个时间步t内进行传播实验，达到稳态时，网络中的节点只有两种状态：易感态S和免疫态R。I(t)和R(t)分别为t时刻网络中处于I态和R态的节点比例。把t和t时刻感染过的节点比例F(t)分别作为横纵坐标，可作出F(t)随t的增大而增大最后趋于稳定的曲线图，不难发现F(t)=I(t)+R(t)。对于同一网络，在相同的感染率β和恢复率λ下，各种重要节点排序算法选取相同数目的排在前列的节点作为感染节点I，越快趋于稳定且具有较大稳态值的排序算法越有效。在Power网络上分别选取重要性排名前5‰、10‰、20‰和50‰的节点，设置感染率β和恢复率λ分别为0.15和0.3，针对SM和LSM等6种重要节点排序算法在50个时间步t内进行SIR传播验证实验（每种算法的传播实验独立运行100次后对F(t)取平均值），实验结果如图4所示。其中，图例中各种算法的F(t)值为该算法在传播达到稳态时的F(t)值。对于图4（d），即选取重要性排在前50‰的节点作为感染节点在整个网络传播，比较6种排序算法（SM、LSM、GM、LGM、DC和BC），达到稳态时，虽然LSM算法的F(t)值仅大于BC算法的F(t)值，但是基于弹簧模型的全局算法SM的F(t)值仅小于DC算法的F(t)值，并且SM曲线的斜率也仅小于DC曲线的斜率，可知SM算法的传播速率和传播范围都仅次于DC算法。尤其对于图4（a）～（c），也就是分别选取前5‰、10‰、20‰的节点作为感染节点，与其他5种排序算法的曲线比较，SM曲线有最大斜率和趋于稳定时的最大高度（最大的F(t)值），反映出SM算法有最快感染速率和达到稳态时的最大感染范围，可知在这两个方面SM算法都好于其他5种排序算法，证明了SM算法较于其他算法更高的合理性和有效性。

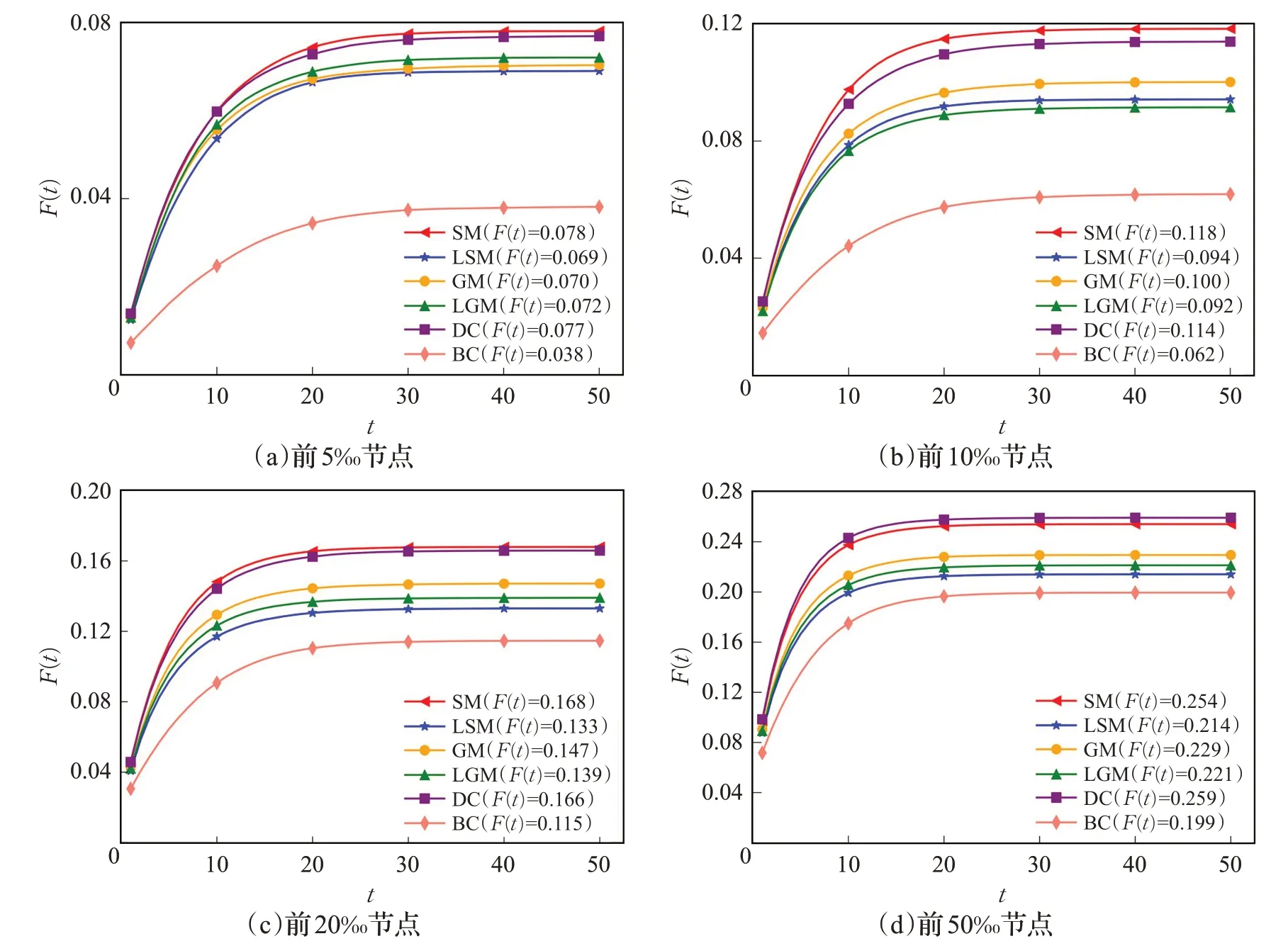
图4 SM和LSM在Power网络上的SIR传播模型验证实验（感染率β=0.15，恢复率λ=0.3）Fig.4 Experiments on SIR epidemic model of SM and LSM on Power network（infected probabilityβ=0.15，recovered probabilityλ=0.3）

3 结束语

本文主要工作是在GM算法和LGM算法的启发下，在弹簧模型的基础上，借助胡克定律，进一步考虑网络中节点近邻信息和路径信息，并结合网络直径，提出了重要节点排序算法SM和其局部算法LSM。在2种合成网络和4种真实网络的基于网络的鲁棒性和脆弱性实验，验证了SM算法和LSM算法对于网络中重要节点排序具有更高的准确性。特别地，在SIR传播模型下，在Power网络上的实验结果证实SM算法得到的排名靠前的重要节点作为一个感染节点集合，与其他算法得到的感染集相比，有更快的传播速度，达到稳态时，有更大的传播范围。SM算法和LSM算法依赖于网络的连通性，后续工作需要针对不连通的网络，考虑对此网络的重要节点排序算法，对其重要节点进行更科学全面的排序。