四足机器人抗重心偏移步态优化

黎晴亮，张志安，马豪男，周何苗

南京理工大学 机械工程学院，南京 210094

科技的进步驱使着机器人技术的全面发展，对于足式机器人相关领域的研究越来越多[1-2]。传统的移动机器人包括履带式、轮式等，对地形要求较高，不适合崎岖路面。而足式机器人由于其高度的灵活性和地形适应性，可以实现在各种不同地形情况下的稳定运动。足式机器人的这一优点让其可以胜任复杂路面下的救援、运送物资等工作。

足式机器人在执行救援、物资运输等任务时，载重会使机器人的重心产生偏移。重心的偏移会对足式机器人的运动稳定性产生影响，严重时甚至会导致步态紊乱、运动崩溃等严重问题。显然，足式机器人具备较强的抗重心偏移能力对提高机器人的动态稳定性有重要作用。

近年来，对于四足机器人重心相关领域的研究多集中在规划重心位置以及计算重心补偿量上。文献[3]提出了一种坡面条件下重心自适应控制算法，在机器人质心原有运动轨迹上加入横向和纵向偏移补偿量，并采用符号微分策略梯度法对质心偏移补偿量进行自动调整，以减少机体翻转扭矩从而提高机器人运动稳定性；文献[4]提出了一种新的稳定性保证方法，通过模型分析法建立机器人的数学及物理模型，从理论角度分析了重心位置对机器人稳定性的影响，从而得出了较为合理的重心位置规划区域，并通过仿真实验验证了改进重心位置规划方法的有效性及合理性。以上对于四足机器人的研究方法依赖于理论分析，这种方法既过于复杂又掺杂众多理想条件，导致结果难以令人满意。与此同时，各类群智能优化算法在四足机器人领域应用颇多。文献[5]提出了一种基于粒子群算法的四足机器人机身横向调整参数优化方法，其以运动过程中机身的横向调整参数为设计变量，目标函数综合考虑了四足机器人躯体稳定性、行走直线性等运动性能，通过该优化算法使四足机器人能够实现具有良好运动性能的静步态；文献[6]利用多目标遗传算法优化CPG单元间的耦合系数矩阵，使得CPG网络的输出信号可以控制机器人关节按照一定的时序发生动作。粒子群算法[7]具有高效、简洁的优点，可以避免复杂的理论建模，因此经常被用于复杂模型下的参数优化问题。本文提出了一种基于改进粒子群算法的抗重心偏移步态优化方法，通过CPG网络控制模型在线生成机器人关节角度，并通过粒子群算法以机器人运动反馈信息为基础不断迭代，进而找出输出模型的最佳参数组合，解决由于重心偏移带来的稳定性问题。

1 模型建立

1.1 四足机器人模型

本文的研究对象为8自由度的四足机器人。为了简化问题，不考虑髋关节的横向自由度，即机器人每条腿均只包含髋关节和膝关节各一个旋转自由度。该机器人前后腿运动模式都采用肘式结构，关节电机类型为舵机，仅需输入位置期望信号即可，四足机器人整体线框图如图1所示。

图1 四足机器人相框图Fig.1 Wireframe of quadruped robot

对四足机器人单腿建立运动学模型如图2所示。

该模型中，以四足机器人髋关节为原点建立笛卡尔坐标系，x正方向为机器人前进方向，y正方向垂直向上，l1和l2分别表示大腿和小腿长度，H为躯干距地面高度，S为步长，h为足端最大离地高度，α为大腿与y轴负方向夹角，β为大腿延长线与小腿之间的夹角，足端坐标为P(x p,y p)。由图2通过几何关系得到单腿逆运动学解算公式为：

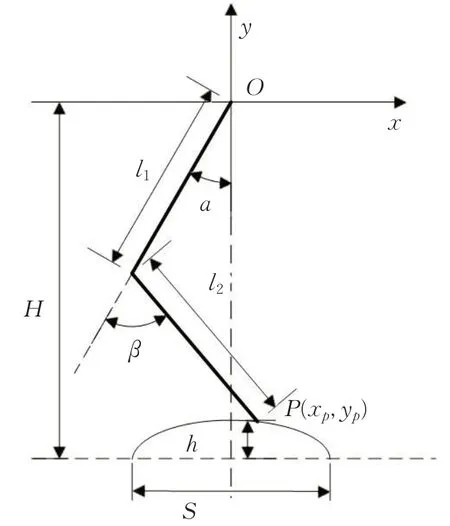
图2 单腿运动学模型Fig.2 Single leg kinematics model

同时以足端摆动相轨迹为摆线，支撑相轨迹为直线作为研究，研究该模型的单腿在两个个完整运动周期里α和β的变化趋势（取单腿步长S为40 mm，摆动相最大离地高度h为20 mm），如图3所示。

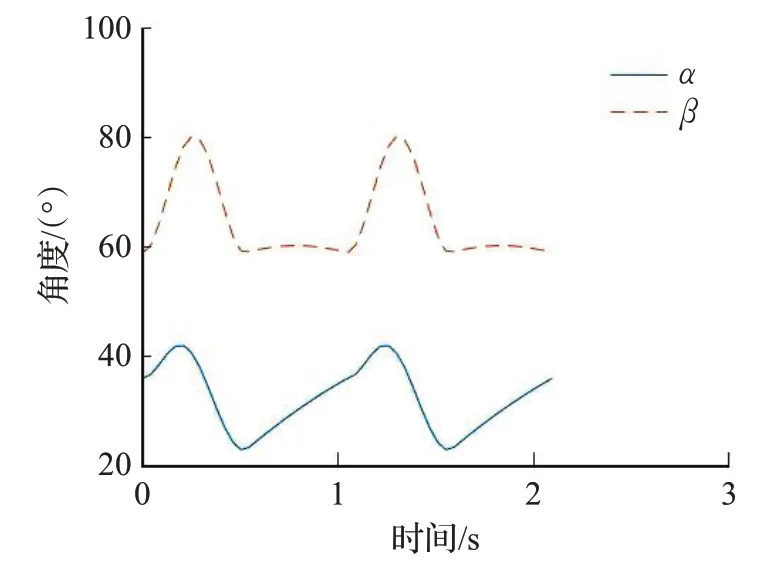
图3 髋关节、膝关节角度变化Fig.3 Changes in angle of hip and knee joints

1.2 Hopf振荡器模型

对于足式机器人的控制，传统方法是将其看成串、并联机器人的模型。这种基于模型的控制方法，误差会逐渐累积并导致不可逆转的错误。近年来，一种基于仿生的控制策略——CPG理论越来越受到研究人员的重视[8-10]。CPG理论试图仿照动物界中普遍存在的节律运动形式，如蜘蛛腿部的运动、蟑螂的行走、人类的呼吸等。CPG理论试图通过建立各种数学模型，从而产生可调的、周期性震荡的信号，使其能够满足节律运动的特点。

CPG的数学模型大致可分为两类：一类是基于神经元模型；另一类是基于非线性振荡器模型，这类方法以单个振荡器为基本研究对象，并通过振荡器自身输出与相互耦合作用来产生可调的信号。常见的基于非线性振荡器的CPG模型有Hopf模型[11-13]、Kuramoto模型等。其中Hopf振荡器的数学模型为：

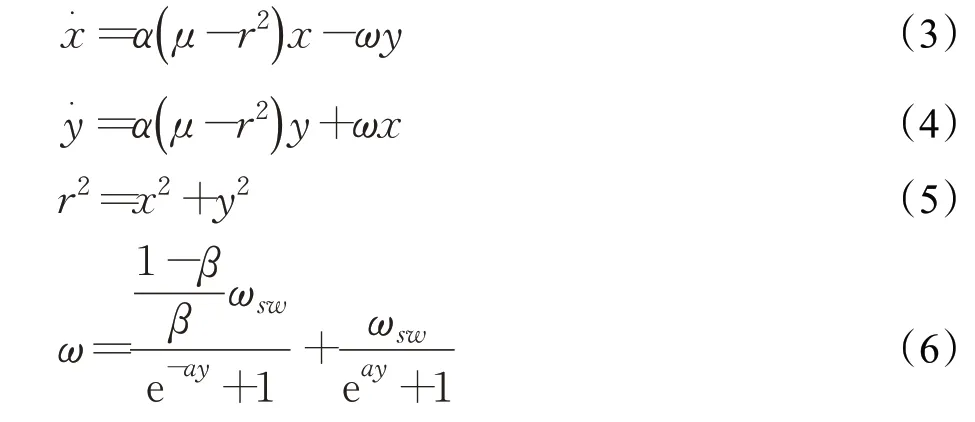
式中α、μ、β、ωsω和a均属于模型参数，用于控制振荡器输出信号x和y。其中α控制振荡器收敛到极限环的速度，μ表示振荡器输出信号的幅值，而β表示足式机器人步态运动中定义的负载因子，ωsω表示摆动相的频率，a决定摆动相和支撑相之间切换的频率。通过对这些参数进行合理的取值，再进行相应的数值变换，便可以使得x和y能够作为足式机器人关节电机的相位控制信号。当β=0.25时单个Hopf振荡器输出信号如图4所示。

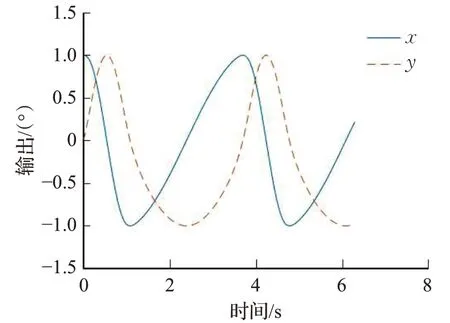
图4 Hopf振荡器输出Fig.4 Hopf oscillator output

观察并对比图3和图4，可以发现图4中Hopf振荡器的输出x和y，其变化趋势近似于图3中α和β的变化趋势。对Hopf模型的参数做相应地调整，并对其输出做一定的幅值、平移以及削波变化，可以尽可能地模拟实际情况下髋关节和膝关节的角度关系，整个过程的示意图如图5所示。本文的仿真实验角度输入采取的都是这种策略，目的是既能保证足端轨迹近似于摆线，提高四足机器人的动态稳定性，又能利用Hopf振荡器模型化、便于构建控制系统的优点。

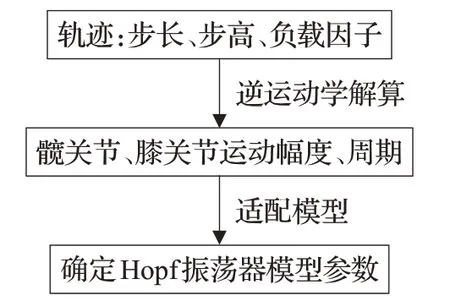
图5 振荡器的输出适配足端轨迹过程Fig.5 Output of oscillator adapted to foot trajectory process

1.3 CPG网络模型

对于四足机器人的控制，每个自由度需要一路输入信号。不仅如此，在四足机器人的步态生成与切换中，不同关节之间的运动关系往往具有相互抑制、相互触发的特性，这就要求各路关节电机的输入信号之间具备一定的耦合性。针对本文中提到的8自由度四足机器人平台，拟采用四路CPG信号来控制整个系统。其中，每个CPG单元控制单条腿，即Hopf振荡器的x输出作为髋关节的角度期望，而y输出通过相应变换后作为膝关节的角度期望。同时通过一个耦合矩阵来表述各振荡器之间的关系。多关节CPG网络结构的拓扑结构如图6所示，数学模型见公式（7）～（10）。

图6 四足机器人CPG网络拓扑结构Fig.6 CPG network topology of quadruped robot

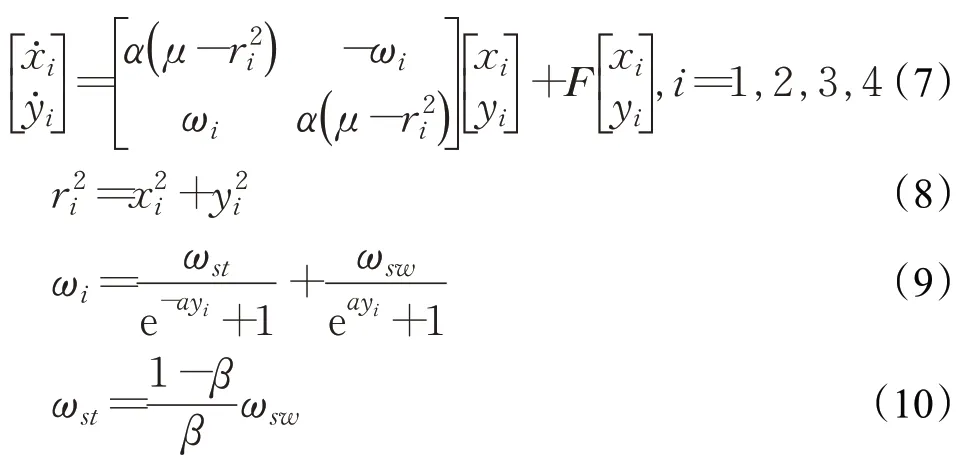
其中，F为一个耦合系数矩阵，用来表示四路Hopf振荡器总共8个输出信号之间的耦合关系。根据上述微分方程组可知F为一个8阶方阵，即：

其中，f ij表示第i项与第j项之间的连接权重，通过对f ij的合理赋值能够调节各CPG单元输出信号的相位关系，从而完成对整个四足机器人的关节协调控制。

2 四足机器人行走实验

2.1 耦合系数矩阵F的赋值

最终的目的是得到具有一定耦合关系的四足机器人关节输入信号，实现四足机器人四条腿的相位耦合。由于本文研究对象为8自由度四足机器人，可只考虑髋关节之间的耦合关系，膝关节输入信号仅跟同路振荡器的髋关节信号相关。根据以上分析可对耦合系数矩阵F做下列设定：

（1）任一膝关节信号对髋关节均没有影响，因此矩阵F中的f12，f14，f16，f18，…，f72，f74，f76，f78均为0。

（2）膝关节仅仅受其所对应的腿的髋关节的影响，因此该矩阵F中第二行、第四行、第六行、第八行中的元素全为0。

（3）再排除自耦合的情况，因此该矩阵对角位置元素全为0。

根据上述原则，耦合系数矩阵变换为下面的一个稀疏矩阵，有效项共有12项。

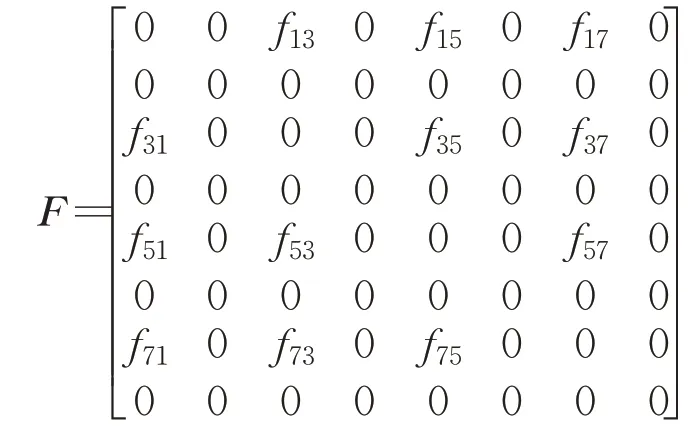
即只需对F中剩余的12项进行合理的取值，便能够调节CPG网络输出信号之间的相位关系，进而控制四足机器人产生相应的步态。下面以四足机器人中常见的trot步态为例，简单说明如何设置耦合系数矩阵F的取值，来产生trot步态所需的关节电机位置输入信号。

所谓“trot”步态，即四足机器人四条腿分成两组，其中对角线上的两组分为同一组，即FL和BR为一组，FR和BL为一组；同组之间两腿同相位关系，不同组之间为异相关系，据此可确定F的值为：

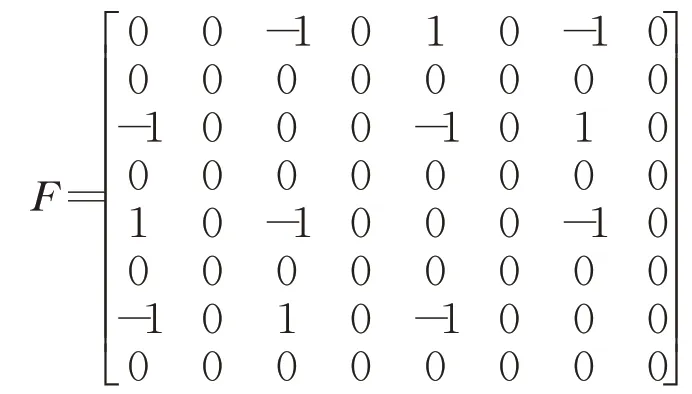
2.2 仿真实验

以walk步态为例，通过足端轨迹规划、单足振荡器模型参数适配（振荡器其他相关参数参考文献[14]）及CPG网络模型的搭建，在MATLAB得到输入信号的数值仿真结果如图7所示。可以看到各关节变化趋势符合walk步态。将得到的walk步态下的CPG网络输出信号应用于仿真实验，四足机器人各项参数指标如表1所示，实际效果如图8所示。为了更好地对机器人的行走稳定性做判定，本实验在四足机器人躯干上增加了IMU节点，在足端增加了力传感器节点，以便更好地收集四足机器人行走过程中的各项数据指标。机器人在平坦路面上行走时，其实时姿态角反馈如图9所示。

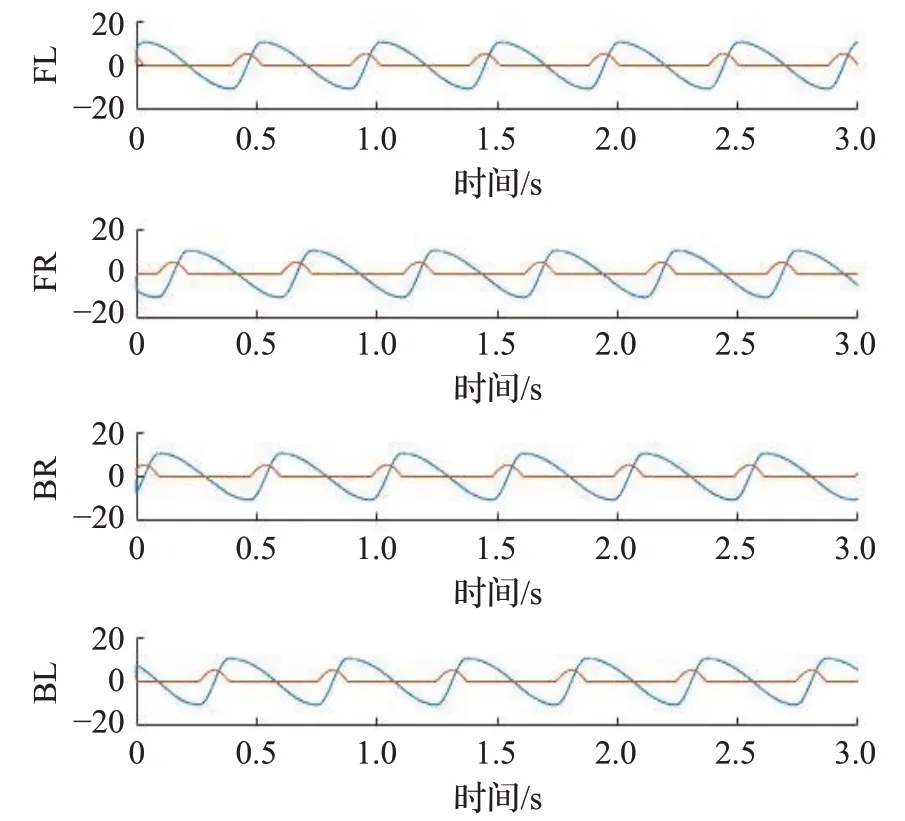
图7 Walk步态信号Fig.7 Walk gait signal

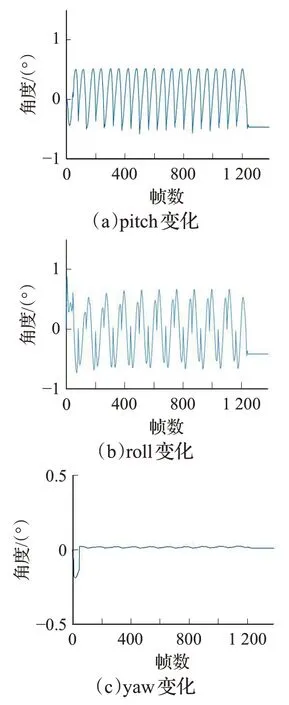
图9 行走实验中的实时姿态角Fig.9 Real-time attitude angle in walking experiment

表1 仿真模型各项参数Table 1 Simulation model parameters

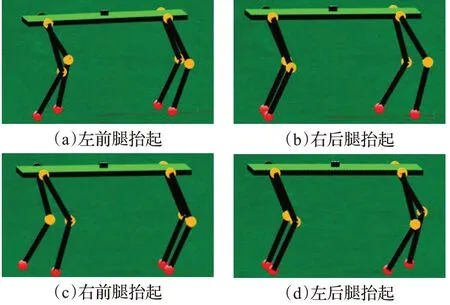
图8 Walk步态行走实验Fig.8 Walk gait walking experiment

从图8中可以看出，机器人行走状态较为稳定：横滚角roll以及俯仰角pitch均呈现微弱的周期震荡的特点，而偏航角yaw的值始终变化不大，证明四足机器人在沿直线行走；而从足端力传感器的反馈来看，以“左前→右后→右前→左后”的顺序交替出现波峰，证明本文设计的CPG网络模型能够生成稳定有效的步态信号。

3 改进粒子群算法的步态优化

为了模拟实际运行过程中的重心偏移现象，在仿真平台中将四足机器人的躯干重心向其前方平移L/8，右侧平移H/8，示意图如图10所示。

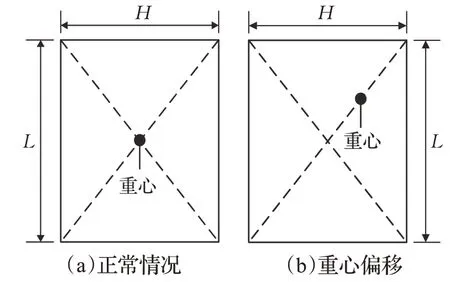
图10 俯视图下的机器人重心偏移情况Fig.10 Offset of robot’s center of gravity in top view

利用控制变量的方法，仅仅在改变重心的情况下再次进行行走实验，四足机器人姿态角如图11所示。由图可发现，四足机器人的姿态角roll、pitch的震荡幅值明显增加，偏航角yaw幅值大幅增加的同时也呈现出非周期性；同时发现机器人在x方向上的位移S X也大大下降。由此可得，重心偏移后的四足机器人在相同步态信号的驱动下，行走稳定性大大下降。

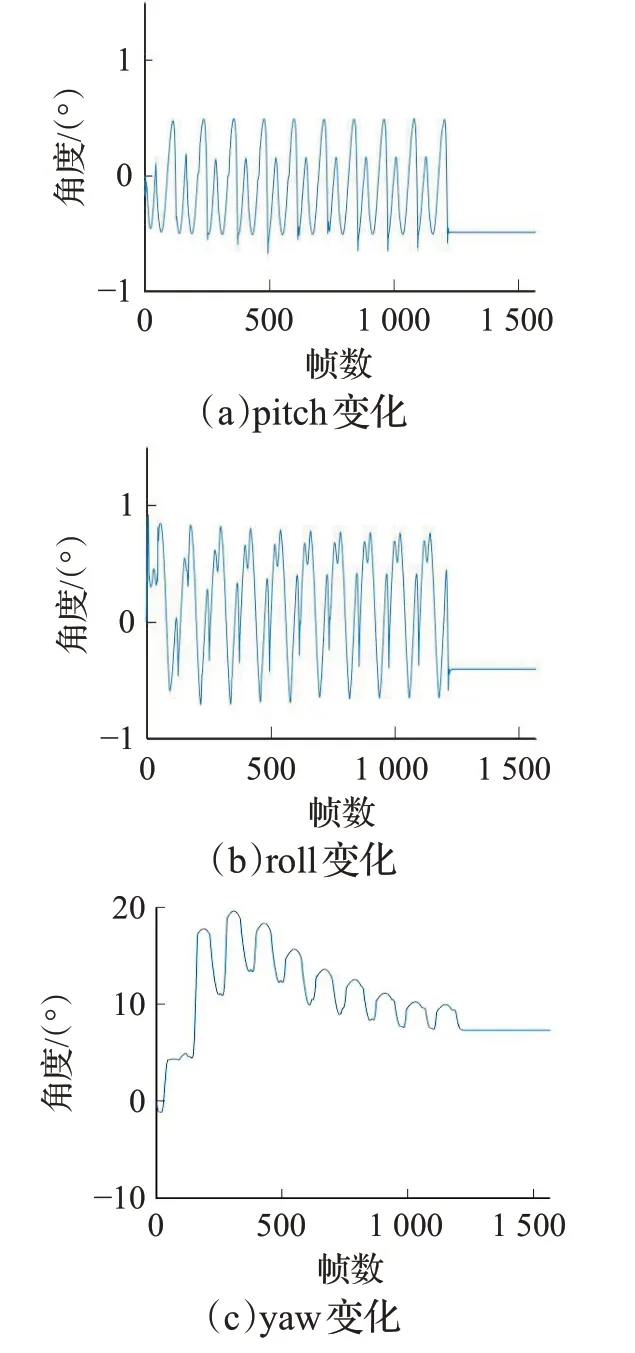
图11 重心偏移后的实时姿态角Fig.11 Real-time attitude angle after center of gravity shifted

本文采用改进粒子群算法对CPG网络模型中相关参数进行优化，进而解决由于重心偏移导致的行走稳定性问题。

3.1 粒子群算法的实现

结合生活实际可知，人负重一侧脚步运动幅度和摆动相频率均会变化。通过这一现象得到启发，本实验将四足机器人负重一侧足端摆线轨迹的步长S、步高h以及摆动频率ωsω这3个参数作为粒子群算法中的待优化变量；由于本实验是MATLAB与webots联合仿真，涉及到数据采集与输入，基于减小工作量的考虑，种群规模不宜选择过大，现将种群规模设为6。对待优化参数的范围进行拉丁方抽样获得的种群初始位置如下：

仿真实验中，四足机器人添加了众多传感器节点，包括：GPS、IMU等。因此，粒子群算法中的目标适应度函数设计主要依赖传感器的数据。经过多次实验，最终确定了目标适应度函数：

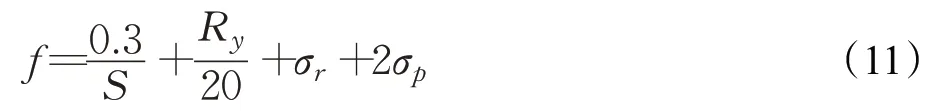
其中S表示四足机器人的在规定时间的行程；R y表示偏航角的极差；σr表示横滚角的标准差；σp表示俯仰角的标准差。

粒子群算法的核心是：每次迭代过程中，根据式（11）来计算每个粒子的适应值，同时更新每个粒子的位置和速度，并从中找出个体最优解和种群最优解，更新公式如下：

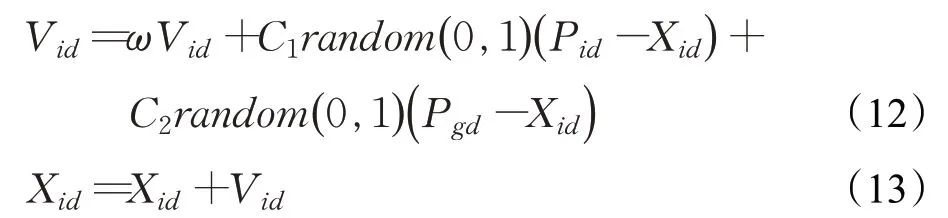
式中，V id表示粒子的速度，X id表示粒子的当前位置，C1和C2分表表示局部加速系数和全局加速系数，Pid表示各单个粒子的历史最佳位置，P gd表示整个种群的历史最佳位置。

3.2 粒子群算法的改进

为了提高PSO算法的收敛速度，达到减少联合仿真工作量的目的，本文设计了一种基于自适应调整权重[15-16]策略的优化方法。式（12）中权重ω代表粒子群算法的全局搜索能力，ω越大则全局搜索能力越强，ω越小则局部搜索能力越强。所谓自适应权重即每次迭代计算中的ω都会随着粒子适应度值的改变而改变，有：

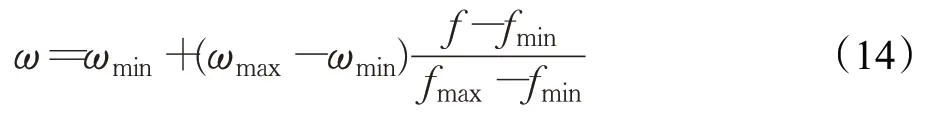
式中，ωmin和ωmax分别表示权重的最小值和最大值，fmax表示上轮迭代计算中粒子的最大适应度，fmin表示最小适应度值。自适应调整权重的策略为：上轮迭代中适应度值f较大的粒子时，相应地增大其权重ω，从而增强PSO的全局搜索能力，继续搜索最优解；而随着粒子适应度值f的减小，越来越接近最优解时，权重ω相应的减小，降低粒子的速度，从而增强PSO的局部搜索能力。

3.3 仿真实验结果及分析

仿真实验过程为：首先对种群进行初始化及更新，同时在MATLAB中构建CPG网络模型并生成步态控制信号；然后导入Webots中的模型进行仿真；最后再对四足机器人所反馈的数据进行分析，并不断进行迭代试验直至各粒子都收敛到同一位置。实验流程图如图12所示。

图12 仿真迭代实验流程图Fig.12 Simulation iteration test flowchart

分别选取实验前期未经优化的粒子和优化后的粒子，对其运动稳定性进行对比分析，结果如表2所示。

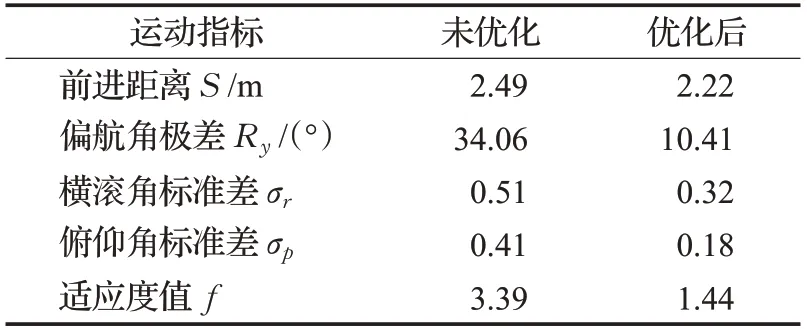
表2 优化前后机器人运动指标Table 2 Optimized robot movement indicators before and after

粒子群算法中各粒子的适应度值是对优化过程中四足机器人运动稳定性的表示。由式（12）可知，越小的适应度值对应的机器人稳定性越好。由表2可以看到，通过粒子群算法优化后，粒子的适应度值大大减小，同时除了前进距离略低于优化前的情况，其他指标均大幅优于优化前。这说明通过粒子群算法迭代搜索出的模型参数组合，能够有效提高四足机器人的运动稳定性。

本实验中粒子的适应度值变化趋势如图13所示。从图13（a）图可以看出，采用未经改进的粒子群算法时，各粒子适应度值总体上随着迭代次数的增加而减小，在经过20次左右的迭代后各粒子的适应度几乎不再变化，达到终止条件。而采用自适应调整权重策略的粒子群算法实验结果如图13（b）所示，可以看到经过改进后的算法在实验结果相同的情况下，具有更快的收敛速度，大大减少了联合仿真的时间，同时也证明本文提出的自适应调整权重策略的有效性。实验后期四足机器人的姿态角较为稳定，直线行走能力也得到提高，这证明粒子群算法在解决多参数优化问题上的有效性。

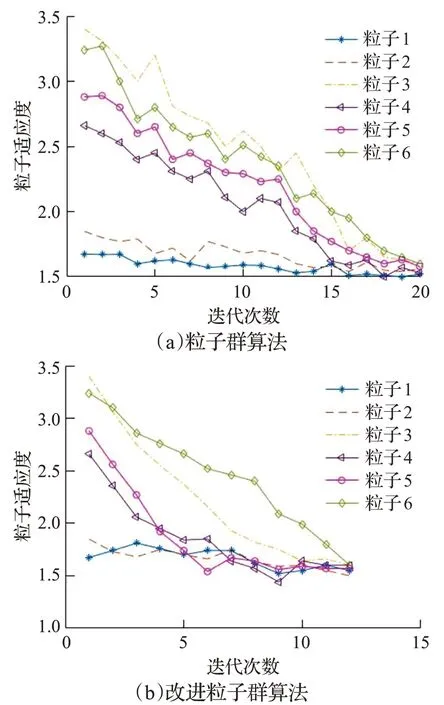
图13 粒子适应度值变化趋势Fig.13 Change trend of particle fitness value

3.4 与多目标遗传算法的对比

遗传算法也常被用于多目标优化问题中。本节将提出的改进粒子群算法和多目标遗传算法分别用于优化CPG网络模型参数。

在遗传算子设计中，变异算子和交叉算子选择均匀变异和均匀交叉模式，选择此模式有利于提高算法的全局搜索能力；选择个体时采用最优个体保存法，即用适应度值最高的Nelite个个体替换适应度值最低的Nelite个个体。多目标遗传算法相关参数设置见表3。为了更好地对比两种群智能优化算法，让多目标遗传算法的种群规模、适应度函数与粒子群算法保持一致。

表3 遗传算法参数设置Table 3 Genetic algorithm parameter setting

表4表示遗传算法和改进粒子群算法多次试验的结果。可以看出，对于相同的优化结果（最小适应度值），虽然遗传算法多次实验的迭代次数较为稳定，但其所需的迭代次数要高于改进粒子群算法，即其收敛速度不如改进粒子群算法；而改进粒子群算法虽然由于种群初始化导致收敛速度不一致，但总体效果好于遗传算法。

表4 算法迭代次数比较Table 4 Comparison of algorithm iterations

4 结论

本文基于Hopf振荡器构建了四足机器人的CPG控制网络。通过单足轨迹规划进而确定CPG数学模型的参数，以CPG网络输出曲线作为四足机器人的输入信号，并进行机器人行走实验证明了所设计CPG网络的有效性；针对实际运行情况下机器人重心偏移导致的运动稳定性问题，利用粒子群算法通过多次迭代搜索运动模型的最佳参数，同时通过自适应调整权重的策略来加快算法的迭代速度，并通过与遗传算法的比较验证改进粒子群算法的有效性，解决了由于重心偏移带来的稳定性问题。