基于作业链的泊位与岸桥协同调度研究

敖 丹，杨勇生

上海海事大学 物流科学与工程研究院，上海 201306

随着集装箱化的发展，海上运输已经成为一种主要的运输方式，全球贸易的80%以上及中国对外贸易的90%左右都是由海运进行处理，集装箱码头在国际运输中发挥着巨大的作用。

整个集装箱码头包括三个区域，即岸边区域、运输区域以及堆场区域。本文研究码头的岸边区域，岸边操作面临的主要问题是泊位分配问题（berth allcation problem，BAP）、岸桥分配问题（quay crane allcation problem，QCAP）和岸桥调度问题（quay crane scheduling problem，QCSP）。泊位分配与岸桥调度具有高度相关性，一方面，泊位分配能够影响到岸桥的调度，船舶的靠泊位置和靠泊时间影响到分配给船舶的岸桥数量以及岸桥的作业时间；另一方面，分配给船舶的岸桥数量以及每台岸桥的装卸效率直接影响到船舶的靠港、离港时间。泊位分配受到岸桥调度的影响，而岸桥调度又依赖于泊位分配的结果，因此，需要对泊位与岸桥进行协同调度研究。

针对泊位与岸桥协同调度问题，国内外学者已经做了大量的研究，主要分为两类：一是泊位与岸桥分配问题（BACAP）；二是泊位岸桥分配与岸桥调度问题（BACAP-QCSP）。关于泊位与岸桥分配问题，Han等[1]考虑船舶到达时间以及集装箱装卸时间不确定的情况下，建立混合整数规划模型，采用基于仿真的遗传算法进行求解。杨春霞等[2]将泊位与岸桥分配问题分为两个子模型并采用遗传算法进行求解，以船舶装卸时间作为耦合变量构建一个外循环将两个子模型耦合起来进行分析。He[3]为了达到节能和省时的平衡，以最小化船舶延迟离港时间和能源消耗为目标建立混合整数规划模型，提出仿真和优化相结合的方法进行求解。Karam等[4]提出了功能集成方法，将问题分为两个子模型进行求解，用反馈回路将模型衔接起来，数值实验验证了此方法的有效性。梁承姬等[5]考虑船舶偏离偏好泊位产生的惩罚时间，通过添加缓冲时间的方法来吸收不确定因素带来的影响。郝杨杨等[6]考虑船舶等待装卸的容忍度约束建立相应模型，用仿真进行分析。Iris等[7]考虑岸桥边际生产率下降以及船舶偏离偏好靠泊位置等问题，通过改进一些约束条件建立模型，采用自适应大邻域搜索（adaptive large neighborhood search，ALNS）启发式算法求解。史立等[8]考虑潮汐对泊位岸桥分配的影响，以最小化船舶延迟成本和岸桥移动成本为目标建立混合整数模型，用CPLEX软件求解。杨劼等[9]考虑离散泊位岸桥调度问题，以最小化船舶总服务成本为目标建立模型，用遗传算法进行求解。焦小刚等[10]考虑了泊位疏浚对泊位岸桥分配的影响，分别用混合遗传、混合粒子群、混合模拟算法进行求解。

关于泊位岸桥分配与岸桥调度问题相关研究，张小莉[11]考虑岸桥混合装卸以及船舶甲板的约束建立泊位岸桥调度模型，设计嵌套式遗传算法进行求解。文献[12]以最小化岸边码头服务成本提出一种新的混合整数规划模型，采用割平面法对模型进行求解。郑红星等[13]考虑大型船需乘潮进出港及岸桥作业约束，构建泊位-岸桥分配主模型以及岸桥调度子模型，设计三阶段混合遗传算法进行求解。毛敏俐等[14]考虑船时效率对泊位分配与岸桥配置的影响，以最小化码头总成本为目标建立模型，用遗传算法求解。Abou Kasm等[15]提出码头作业一体化的数学公式，考虑任务优先级与岸桥动态、静态配置不同组合场景下的岸桥操作策略对码头作业进度的影响。Tasoglu等[16]首次考虑混合泊位布局、船舶动态到港、装卸作业时间不确定以及岸桥作业无冲突等因素建立仿真优化模型，用仿真与模拟退火相结合的方法进行求解。文献[17]考虑了船舶的水深、潮汐条件以及岸桥之间的安全距离，建立泊位与岸桥联合调度混合整数规划模型，采用基于环状拓扑粒子群算法对大规模问题进行求解。

从上述文献中可以发现，泊位岸桥协同调度问题已有广泛研究，其中大多数学者主要研究泊位与岸桥之间的分配问题，而关于岸桥如何装卸集装箱的作业调度问题研究较少。本文不仅研究泊位岸桥分配问题，还考虑岸桥间的相关约束以及岸桥任务之间的均衡，进一步研究岸桥装卸作业调度问题，建立泊位岸桥分配和岸桥调度两个模型，关注两个模型之间的反馈，并设计嵌套式循环算法求解。此外，本文采用作业链的方法，引入“链式优化”思路，用链单元、链环节、链上界面与链下界面等概念来理解泊位岸桥协同调度问题。

1 问题描述

对于陆续进港的船舶，港口规划者需要根据给定的船舶信息以及码头的实际情况为船舶安排泊位时间、泊位位置，根据船舶的装载量安排合理的岸桥数量。如图1是一个泊位计划时空图，图中的矩形表示相应的船舶，矩形中的数字分别表示船舶编号和分配给此船的岸桥数量。

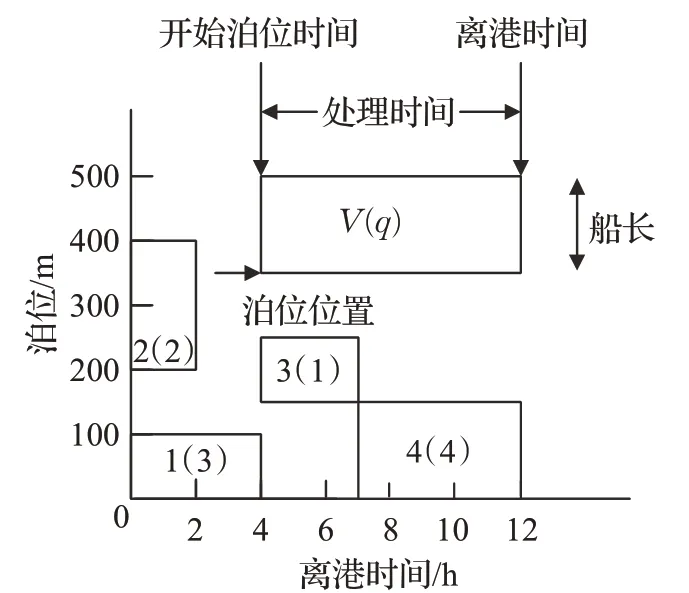
图1 泊位计划时空图Fig.1 Space time diagram of berth planning

当船舶靠港后，需要安排岸桥对船舶进行装卸作业，岸桥调度决定了岸桥进行装卸作业的顺序，岸桥调度将每艘船划分为一组贝位，每个贝位上都载装集装箱，港口规划者需要将船舶的贝位任务分配给相应的岸桥组，考虑到岸桥相互干扰以及各个贝位任务的时间窗等因素来确定岸桥的装卸作业顺序。只有当岸桥全部装卸完集装箱后船舶才能离港，船舶离港后岸桥闲置，可以安排为其他船舶进行服务。

作业链是指相互联系的一系列作业活动组成的链式结构。集装箱装卸作业环节包括泊位分配、岸桥作业、AGV作业、场桥作业、外集卡作业等，每个作业环节都是相对独立的链单元，每个链单元都由链上界面、链环节和链下界面组成。在优化链单元时，不仅要注重链单元内的优化，也要考虑到作业链的整体性能。

本文只考虑卸船作业，故泊位与岸桥协同调度问题中所涉及到的作业链主要由泊位链单元和岸桥卸船作业链单元组成，其中泊位链单元主要为动态到港船舶分配靠泊时间、靠泊位置和岸桥数量，对此拟采取资源节点优化策略进行分析；岸桥卸船作业链单元主要是将船舶贝位任务分配给相应的岸桥组以及确定每台岸桥的装卸作业顺序，对此拟采取任务节点优化策略进行分析。考虑到作业链的整体性能，采用嵌套循环算法对模型求解，确定最佳的泊位岸桥协同调度方案。

2 模型建立

泊位岸桥协同调度问题涉及的变量和参数众多，为更好地优化泊位和岸桥的性能指标，本文将此问题分为泊位岸桥分配问题和岸桥调度问题，建立两个模型分别进行优化，然后用岸桥数量作为公用变量将模型连接起来进行协同优化。

2.1 泊位岸桥分配模型

采用资源节点优化策略，将泊位作为作业链的开始链单元，其中泊位上界面由船舶确定，船舶的到港时间、吃水深度、船时效率要求分别对应泊位上界面的靠泊时间、水深条件、泊位作业能力；链环节为船舶制定靠泊计划，包括靠泊顺序和靠泊位置；泊位下界面受岸桥、堆场等影响，岸桥所在位置决定泊位的作业能力，进口箱对应的堆场位置决定船舶的偏好靠泊位置。如图2表示的是泊位链单元结构图。

图2 泊位链单元结构示意图Fig.2 Schematic diagram of berth chain unit structure

2.1.1 假设条件

（1）时间周期划分为相等的时间段，泊位划分为同等的泊位段；

（2）船舶一旦停泊，泊位位置固定；

（3）每艘船都只有一个偏好靠泊位置；

（4）岸桥之间不能相互跨越，都有一定的安全距离；

（5）船舶装卸作业不能在中途停止，每艘船舶接受服务的岸桥数目有最大最小数量限制。

2.1.2 参数设置

集合：

V为到港船舶集合，i,g∈V={1,2,…,n}；B为泊位段集合，k∈B={1,2,…,L}；

T为时间段集合，t∈T={1,2,…,H}；

Ri为第i艘船的岸桥数量集合

参数：

n为船舶总数；

L为泊位段总数；

H为时间段总数；

q为岸桥总数；

a i为第i艘船的预计到达时间；

d i为第i艘船的预计离港时间；

b i为第i艘船的偏好靠泊位置；

mi为第i艘船的岸桥需要工时数量；

l i为第i艘船的长度；

c1i为每单位等待时间成本率；

c2i为每单位延迟离港时间成本率；

c3i为每单位偏离理想泊位位置的成本率；

c4为岸桥运营的每小时成本率；

α为岸桥之间的干扰指数；

β为泊位偏差系数；

M为一个足够大的数。

决策变量：

S i为整数，第i艘船的开始靠泊时间；

Ei为整数，第i艘船的实际离港时间；

P i为整数，第i艘船的实际靠泊位置；

ΔBi为整数，当第i艘船靠泊在b i位置时与其偏好靠泊位置之间的偏差；

M it为0-1变量，第i艘船在t时间段内有岸桥分配则为1，否则为0；

Ritr为0-1变量，第i艘船在t时间段内分配r台岸桥则为1，否则为0；

G itk为0-1变量，第i艘船在t时间段内靠泊在第k个泊位则为1，否则为0；

Y ig为0-1变量，如果第i艘船泊位在第g艘船的下方则为1，否则为0，如b i+l i≤b g；

Z ig为0-1变量，如果第i艘船的结束时间不晚于第g艘船的开始时间则为1，否则为0。

2.1.3 目标函数及约束条件

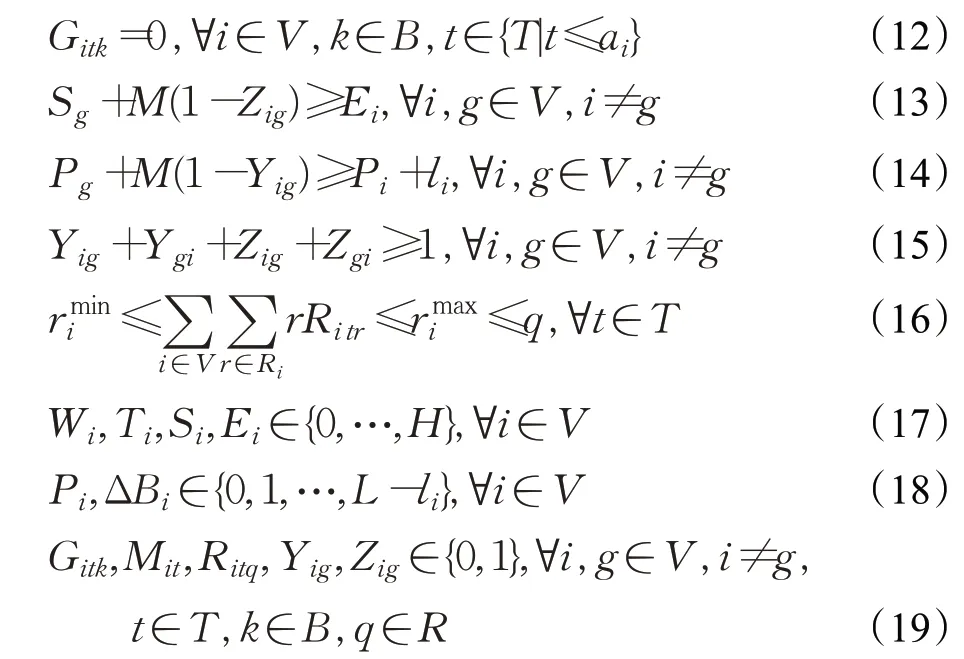
式（1）是目标函数，即最小化船舶总的服务成本，包括等待靠泊的时间成本、延迟离港的时间成本、偏离偏好靠泊位置的惩罚成本以及岸桥作业成本；式（2）和（3）分别表示等待时间和延迟时间决策变量；式（4）和（5）表示船舶靠泊位置的偏差变量；式（6）表示考虑到岸桥干扰造成的效率损失以及船舶靠泊位置的偏差，确保每艘船都能获得所需的岸桥工时；式（7）表示分配的岸桥数量与船舶靠泊之间的关系；式（8）表示船舶i的在泊时间应等于该船舶进行岸桥作业的所有靠泊时间之和；式（9）和（10）表示船舶i开始靠泊和离港时间的界限；式（11）表示每艘船只能在一个时间段内靠泊；式（12）表示船舶i在未到达港口之前不能靠泊；式（13）表示船舶i离港后船舶g才能靠泊在此处；式（14）表示船舶i需靠泊在船舶g的下方；式（15）避免船舶在时间和空间上重叠；式（16）表示分配给船舶的岸桥数量的约束；式（17）～（19）是定义相关变量的取值范围。

2.2 岸桥调度模型

对于进口箱卸船作业环节，该环节的上、下作业环节分别为船舶靠泊作业和AGV作业，因此岸桥卸船作业的时间窗的最早开工时间为泊位的最晚完工时间，时间窗的最晚完工时间为AGV的最早开工时间。

2.2.1 假设条件

（1）只考虑进口箱卸船作业；

（2）所有岸桥的工作效率、移动速度相同；

（3）贝位和岸桥的顺序索引从船头到船尾依次递增；

（4）岸桥在给定时间内只能在一个贝位作业，只有完成当前贝位任务才能移动到下个贝位；

（5）不考虑装卸过程中船舶平衡问题和岸桥等待AGV的时间；

（6）岸桥初始作业时刻、初始位置已知。

2.2.2 参数设置

集合：

Z为集装箱集合，u,v∈Z={1,2,…,z}；

E为贝位集合，m,o∈E={1,2,…,e}；

Q为岸桥集合，j,p∈Q={1,2,…,q}。

参数：

z为待处理的集装箱数量；

e为贝位总数；

q为岸桥总数；

I为虚拟开始任务I∈{0}；

F为虚拟结束任务F∈{E+1}；

L u为集装箱u所在贝位的编号；

c jmo为相邻贝位移动时间；

k jm为岸桥j处理贝位m的时间；

p jmo为岸桥j处理贝位m和贝位o之间的时间间隔。

决策变量：

X ju为0-1变量，岸桥j处理集装箱u则为1，否则为0；

S jmo为0-1变量，岸桥j在处理完贝位m之后立即处理贝位o则为1，否则为0；

Z jm为0-1变量，岸桥j处理贝位m则为1，否则为0；

h jm为整数变量，岸桥j开始处理第m个贝位的时刻；

r j m为整数变量，岸桥j处理完第m个贝位的时刻；

为整数变量，岸桥j在T时期的位置。

2.2.3 目标函数及约束条件

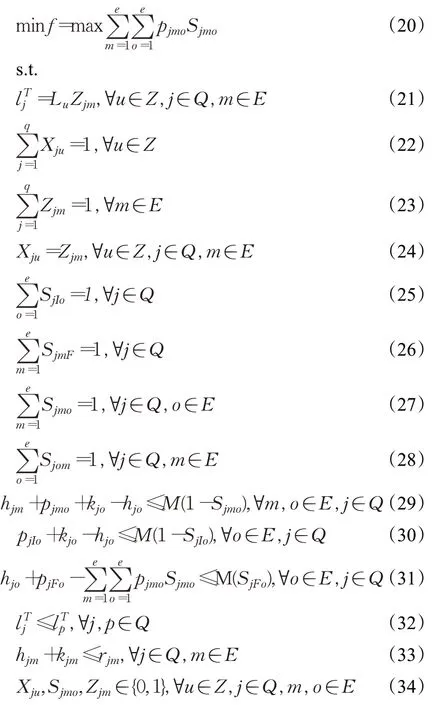
式（20）是目标函数，即最小化岸桥最大完工时间；式（21）表示岸桥j在t时期所在的贝位位置；式（22）表示每个集装箱只能由一台岸桥处理；式（23）表示每个贝位只能由一台岸桥处理；式（24）表示同一贝位的集装箱由同一岸桥服务；式（25）和（26）表示每个岸桥必须处理一个开始任务和一个结束任务；式（27）和（28）表示每个贝位任务只有一个前序任务和一个后序任务；式（29）表示每个任务的完成时间；式（30）表示岸桥的开始时间；式（31）表示岸桥的结束时间；式（32）表示岸桥之间不能交叉；式（33）表示岸桥开始时间与岸桥完工时间的关系；式（34）和（35）定义决策变量。

3 算法设计

基于上述模型相互作用的特点，采用嵌套循环算法[2]进行求解，首先将泊位岸桥分配模型和岸桥调度模型看作两个内循环，用遗传算法分别求解，遗传算法流程如图3所示；然后为了提高作业链的整体性能，构建一个外循环对两个模型同时优化求解，用岸桥数量作为公用变量进行传递和反馈。嵌套循环的主要过程如图4所示，首先设置初始岸桥数量得到泊位岸桥分配解，带入到岸桥调度模型中得到岸桥调度解，然后将此解反馈到泊位岸桥分配模型中，对泊位岸桥分配计划进行调整，通过反复迭代和反馈，不断改进解的质量，从而得到最佳的泊位岸桥协同调度方案。

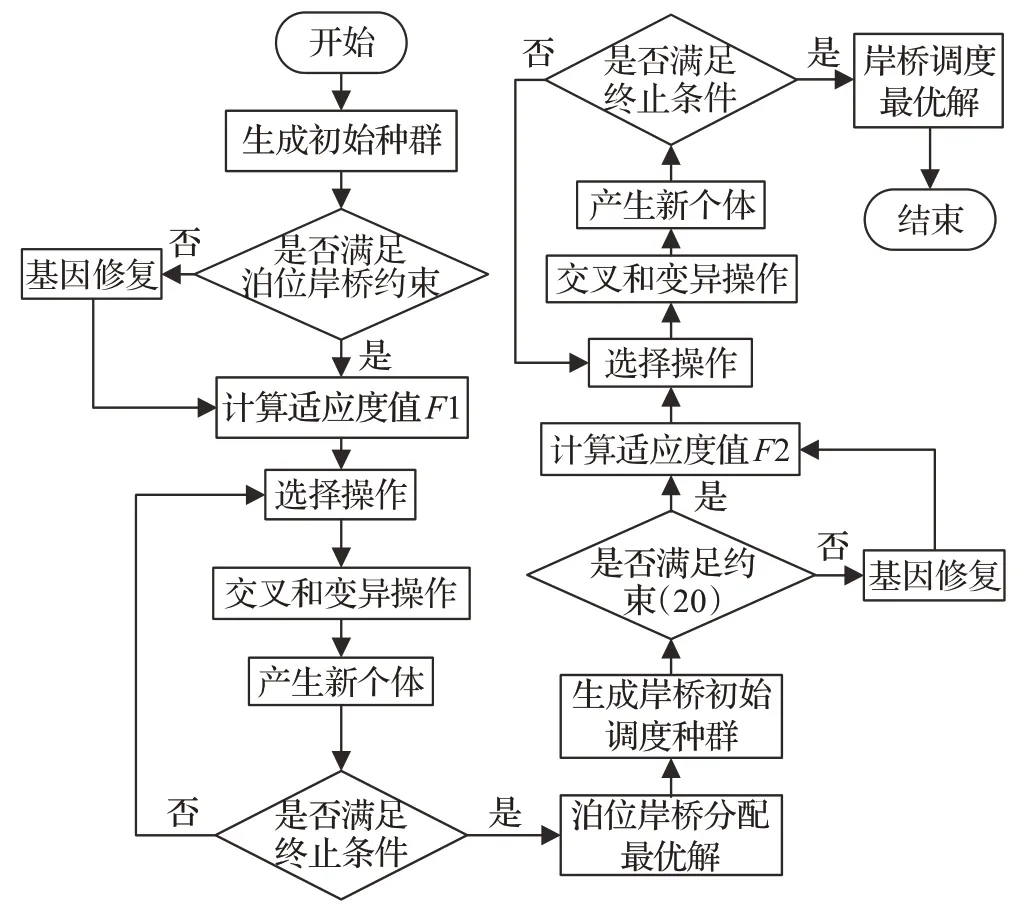
图3 遗传算法流程图Fig.3 Flow chart of genetic algorithm

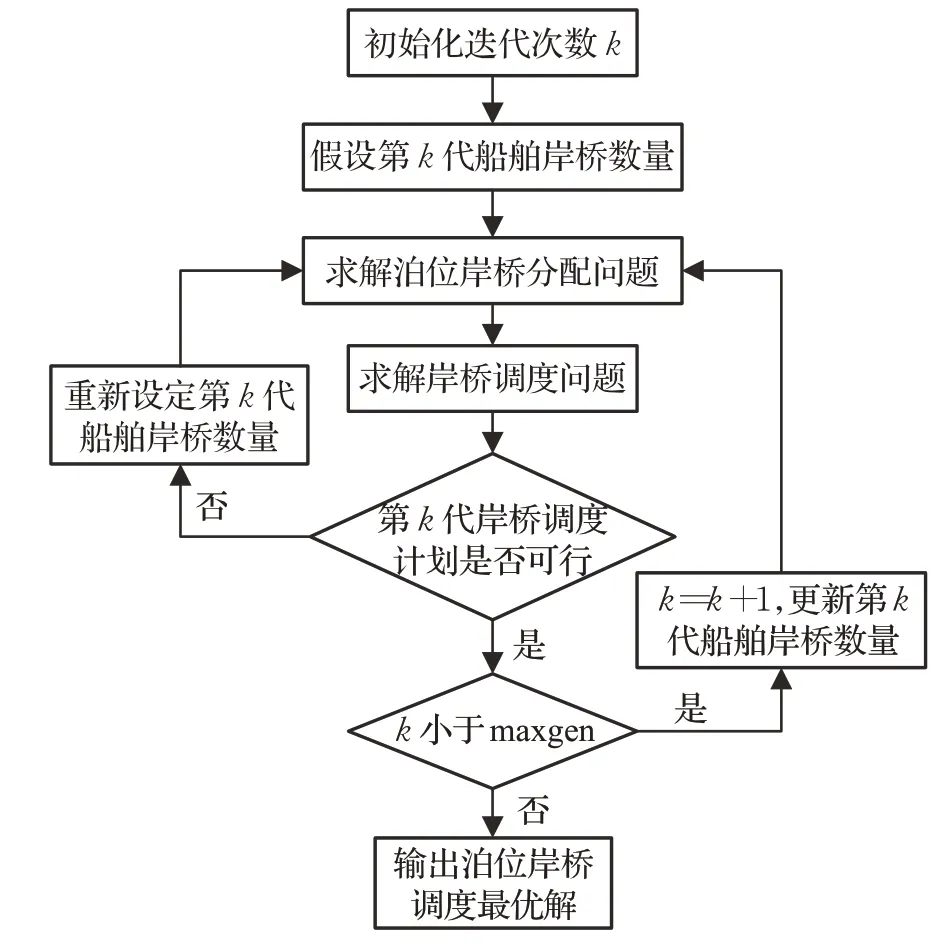
图4 嵌套循环算法流程图Fig.4 Flow chart of nested loop algorithm

3.1 泊位岸桥分配模型求解

（1）染色体编码与初始化种群

采用实数编码的形式，按照船舶的到港时间顺序进行编码。如图5所示，染色体包括三部分：一是随机生成的船舶靠泊顺序；二是船舶的靠泊位置，在[0，L-l i]之间生成；三是分配给船舶的岸桥数量，介于最小和最大岸桥数量之间，并且不超过码头总岸桥数量。

图5 染色体构造Fig.5 Chromosome structure

（2）适应度函数设置

为避免陷入局部最优，引入岸桥移动启发式规则计算适应度，适应度函数值取目标函数的倒数，fitness=1/f，即最小化船舶在港服务总成本的倒数。

（3）选择操作与交叉操作

采用轮盘赌法进行选择操作。采取顺序交叉的方法进行交叉操作，如图6所示，从种群中选取两个父代个体，随机选择两个交叉列，按照船舶的编号顺序进行对应部分的交叉操作。

图6 交叉操作Fig.6 Cross operation

（4）变异操作

随机选择父代个体的两个基因值，将这两个值进行互换，产生新的个体，变异操作过程如图7所示。

图7 变异操作Fig.7 Variation operation

3.2 岸桥调度模型求解

（1）染色体编码

采用矩阵式编码，染色体由m行n列的矩阵表示，其中m表示分配的岸桥数量，n表示船舶的贝位数。染色体中的基因值表示分配给此台岸桥的贝位上的集装箱数量，0表示没有可处理的集装箱。如图8为染色体构造，有3台岸桥和12个贝位。

图8 染色体构造Fig.8 Chromosome structure

（2）适应度函数设置

目标函数为最小化岸桥最大完工时间，适应度函数取该目标函数的倒数。

（3）选择操作与交叉操作

采用精英保留策略，在种群中选取适应度函数值较好的个体直接保留到下一代。

采用算术交叉的方法产生新的染色体，参考文献[18]提出的交叉策略方法，交叉过程如下：off spring=φ×parent1+(1-φ)×parent2，本文设置φ=0.8，交叉过程如图9所示。

图9 交叉操作Fig.9 Cross operation

（4）变异操作

与泊位岸桥分配中的变异操作一致。

4 算例结果与分析

4.1 初始数据

码头岸线总长1 200 m，50 m为1个泊位段，共24个泊位段；船舶计划周期为24 h；10台可用岸桥；岸桥的作业效率为1 TEU/min；岸桥在相邻贝位之间的移动时间为1 min，安全距离为1个贝位；岸桥的干扰系数为0.9；泊位偏差系数为0.2；单个集装箱偏离偏好泊位每米的成本为0.01元；船舶的成本参数分别为：c1i=100，c2i=100，c3i=100，c4j=150。初始岸桥数是根据船舶集装箱数和岸桥的工作效率计算所得，并符合最小和最大岸桥数的约束。

船舶的相关信息见表1所示，船舶的到港时间、偏好靠泊位置、船舶贝位数都是随机生成的，每个贝位的作业量生成的范围介于[30，100]之间。

表1 船舶信息表Table 1 Ship information table

4.2 结果分析

内循环中遗传算法的参数设置如下：泊位岸桥分配模型中种群规模为100，迭代次数为300，交叉和变异概率分别为0.8和0.1；岸桥调度模型中种群规模100，迭代次数200，交叉和变异概率分别为0.9和0.2。外循环中的最大迭代次数为500，用MATLAB软件进行编程对模型求解，泊位岸桥分配模型中算法收敛如图10所示，可以看出算法迭代至125代时目标函数值趋于收敛至最优解。得出泊位岸桥分配最优解，如表2所示，并绘制了泊位岸桥分配计划图，如图11所示，此图更加形象直观地表达了计划周期内各到港船舶的靠泊时间、靠泊位置、分配的岸桥数量以及船舶的离港时间。

图11 泊位岸桥分配计划Fig.11 Berth quay crane allocation plan

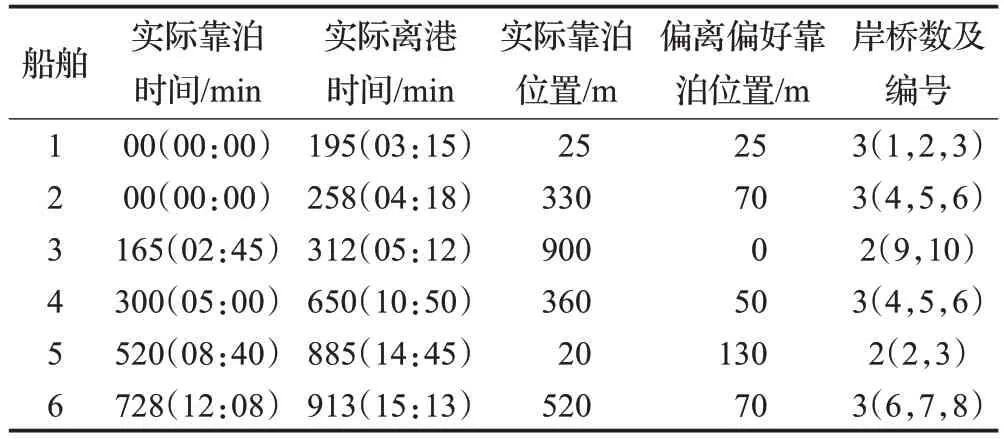
表2 泊位岸桥分配结果Table 2 Berth quay crane allocation results

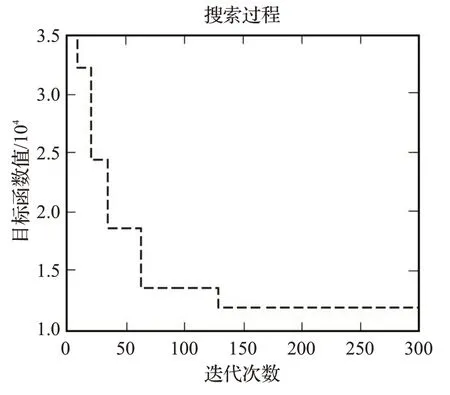
图10 结果收敛图Fig.10 Result convergence graph

根据泊位岸桥分配的结果，可以计算出每艘船舶所花费的成本，见表3，从表中可知6艘船舶在港期间所花费的总成本为12 303元。

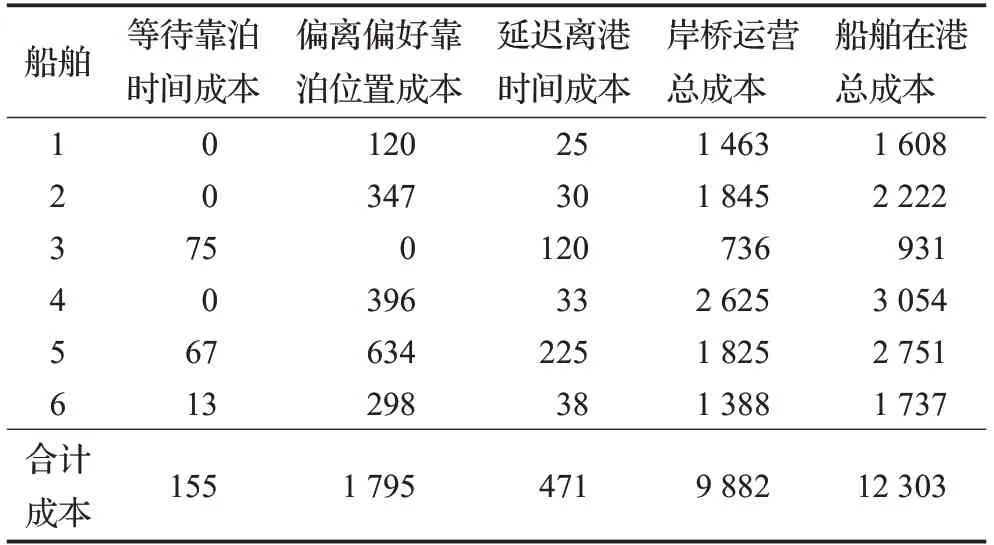
表3 船舶成本分析Table 3 Ship cost analysis 元

在泊位岸桥分配的基础上，结合表4中到港船舶的贝位作业量以及岸桥相关信息，对岸桥调度模型求解，得出如图12所示的岸桥调度图，图中横轴表示岸桥作业时间，纵轴表示船舶贝位，此图表示了计划周期内岸桥的作业调度过程，包括每台岸桥的开工时间、作业时间以及完工时间，从图可知6艘船舶各自的开工时间分别为0、0、165、300、520和728 min，完工时间分别为195、258、312、650、885和913 min。

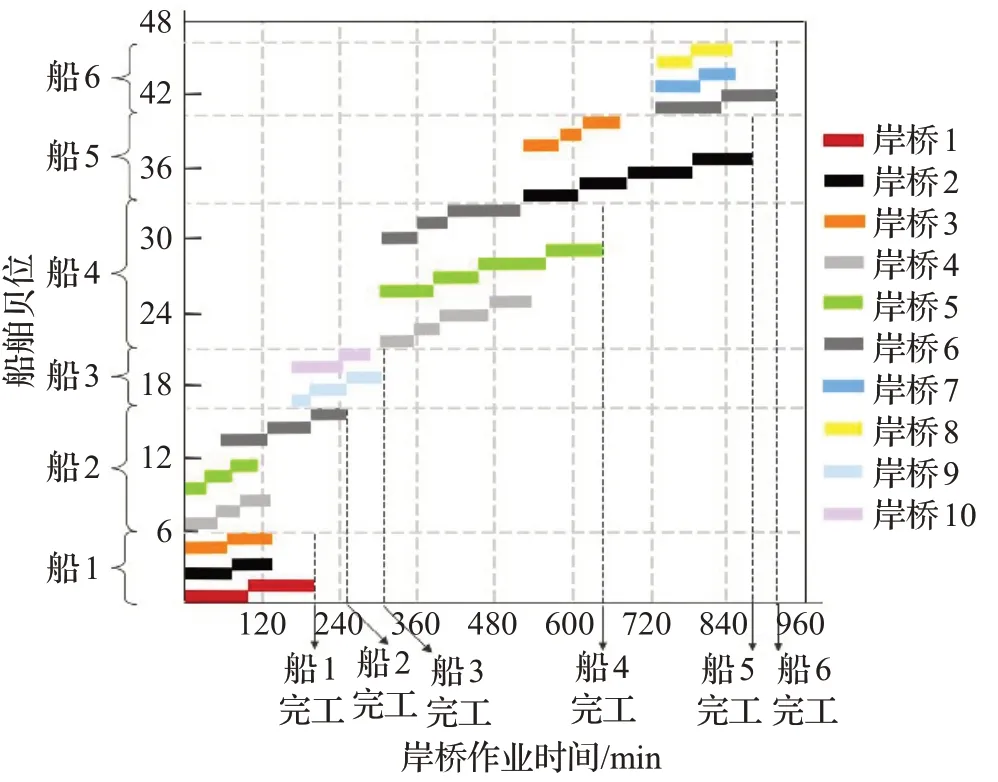
图12 岸桥调度图Fig.12 Quay crane dispatching chart

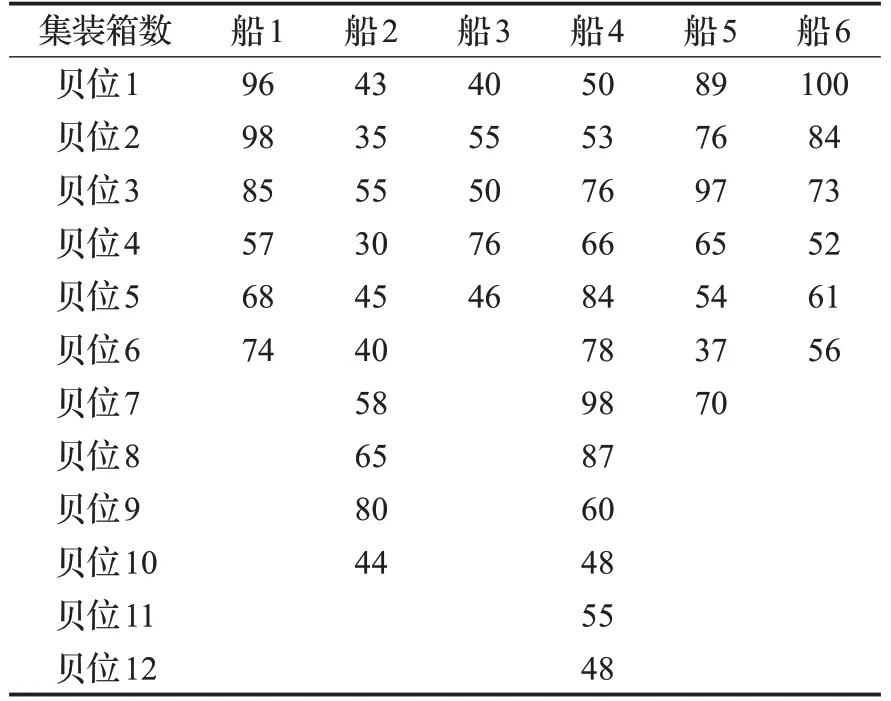
表4 任务船舶贝位以及集装箱数量Table 4 Number of mission vessels and containers

4.3 单独调度与协同调度对比分析

泊位与岸桥调度问题能单独优化，也可以协同优化，为了说明协同调度的有效性，对此问题进行单独调度，即将泊位岸桥分配和岸桥调度当成两个独立的阶段进行考虑，只单方面考虑泊位岸桥分配对岸桥调度的影响，目标函数成本比较如表5所示。

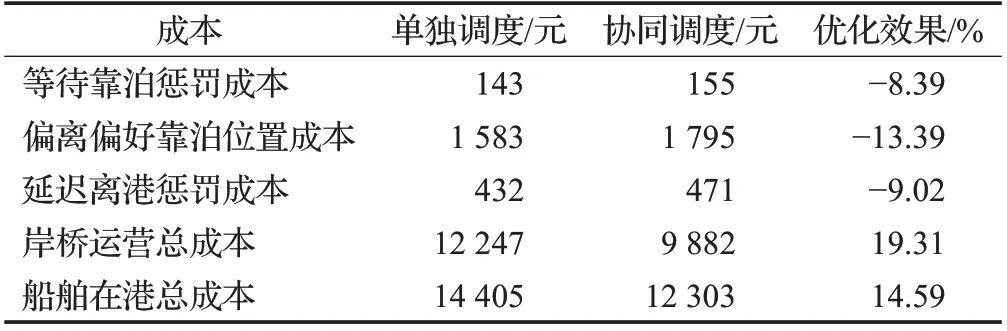
表5 成本比较Tab.5 Cost comparison

从表中可看出，协同调度的优化效果主要表现在岸桥运营总成本上，这是因为本文将岸桥调度问题一起考虑，确定了最佳的岸桥装卸作业顺序，提高了岸桥的装卸效率，从而减少了船舶在港总成本。

4.4 不同规模算例结果

为了验证模型和方法的有效性和普适性，随机选取6个算例进行实验，每个算例运行10次取平均值，与单独调度进行对比，实验结果见表6，其中n表示船舶数量，e表示贝位数，q表示岸桥数。

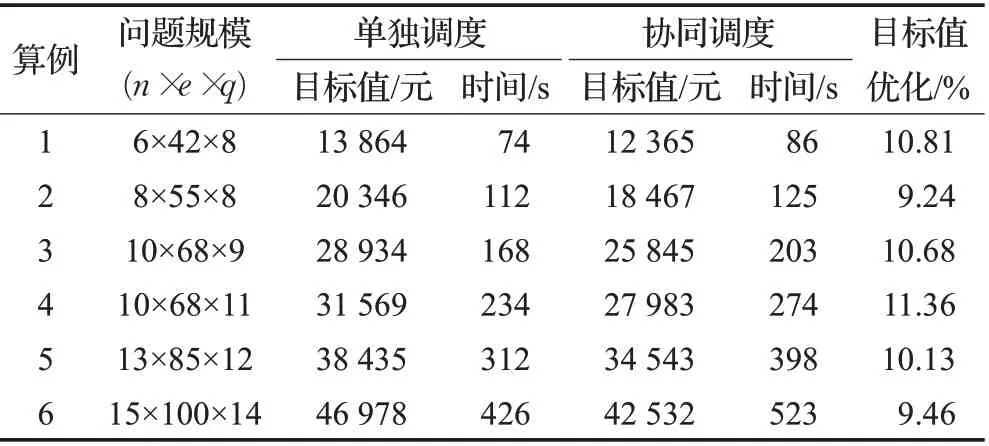
表6 算例结果对比Table 6 Comparison of calculation results

由算例1和2可知，岸桥数量不变时，船舶数量越多，船舶在港总成本和算法求解时间会逐渐增加；由算例3和4可知，船舶规模一定时，分配的岸桥数量越多，算法求解时间越久，船舶在港总成本并没有减少，这说明岸桥数量不是越多越好。此外，与单独调度相比，协同调度在求解时间上要更久，但其优化效果更好，平均可以达到10.28%的优化效果。

4.5 算法对比

为了验证遗传算法的有效性，随机选取6个不同规模的算例分别与粒子群算法（PSO）、蚁群算法（ACO）和蜂群算法（ABC）进行对比分析，考虑到随机误差，每个算例运行10次取其平均值，实验结果见表7。

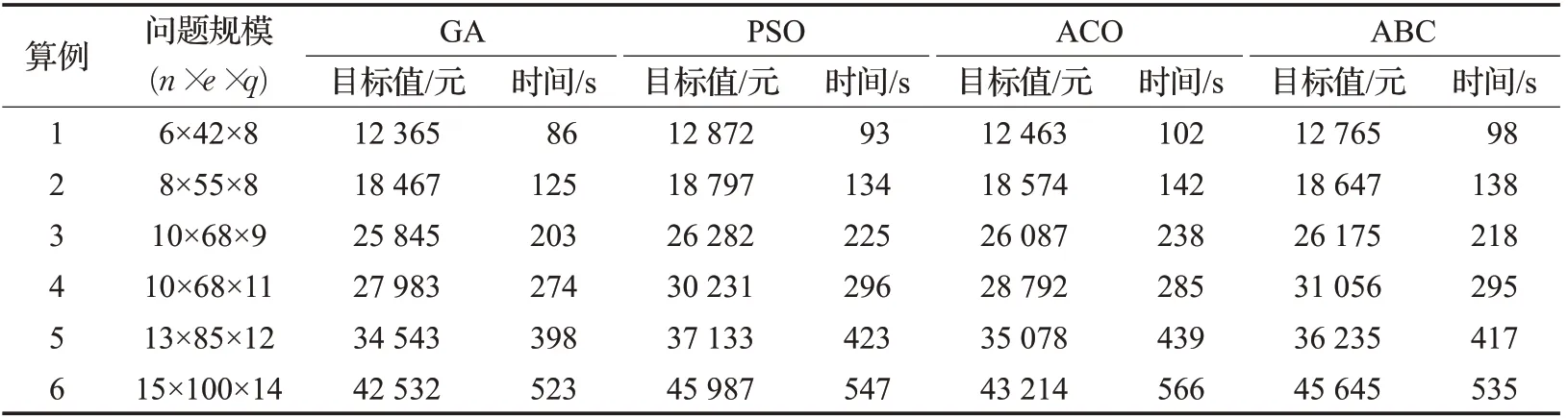
表7 算法对比结果Table 7 Algorithm comparison results

从表7中可知，中小规模下这些算法都能得到最优解，随着问题规模变大，算法求解时间变长，与其他智能算法相比，遗传算法在求解时间上花费的时间相对更少，说明遗传算法求解效率要更高。从图13可看出，目标函数值的变化幅度随问题规模变大而增加，粒子群算法与蜂群算法变化幅度稍大，而遗传算法变化趋势较平稳，说明遗传算法求解质量更好，适合大规模问题求解。由此可知，遗传算法在求解质量和效率上都更优，从而验证了遗传算法在求解此类问题中的有效性和稳定性。

图13 算法表现分析Fig.13 Analysis of algorithm performance

5 结束语

本文从作业链的角度对泊位与岸桥协同调度问题进行研究，首先将泊位计划看作一个链单元，采用资源节点优化策略分析，建立泊位岸桥分配模型；然后将岸桥卸船作业看作一个链单元，采用任务节点优化策略分析，建立岸桥调度模型。考虑作业链的整体性能，采用嵌套循环算法对模型同时求解，内循环用于求解两个模型，外循环通过两个模型之间的反馈得到协同调度最优解。为了验证本文提出的模型和算法的有效性，扩大问题规模，设计不同的算例进行分析，实验结果表明：（1）与单独调度相比，协同调度平均可达到10.28%的优化效果，通过合理利用泊位与岸桥资源，显著降低了岸桥成本，进而减少船舶在港总成本。（2）通过与粒子群、蚁群算法、蜂群算法进行对比，结果表明遗传算法在求解质量和求解效率上都更优，证明了遗传算法适合求解此类问题。

本文只考虑了卸船作业，未来可与装船作业结合起来进行研究，使其更加符合码头实际的生产作业；对于问题求解，采用遗传算法，未来可以对遗传算法进行改进或采取其他更加高效的算法进行求解。