高阶马尔科夫链极限概率分布的一种松弛算法
宋素华,喻高航
(杭州电子科技大学理学院,浙江 杭州 310018)
0 引 言
马尔科夫链(Markov Chain)[1]是状态空间中从一个状态转移到另一个状态的随机过程,广泛应用于DNA序列分析[2]、多重线性Pagerank[3]、风力机设计[4]、排队系统[5]等领域,是分析随时间变化的各种随机(概率)过程的有力工具。高阶马尔科夫链是一阶马尔科夫链的高阶推广,近年来,关于高阶马尔可夫链的极限概率分布问题的相关研究取得了不少成果。文献[6]提出一种快速求解稀疏马尔可夫链极限概率分布的算法。文献[7]研究了用高阶幂法(Higher Order Power Method,HOPM)求解马尔科夫链的极限概率分布问题,给出了算法的收敛性分析,并在一定条件下建立了高阶马尔可夫链的极限概率分布向量的存在性和唯一性。文献[8]在高阶幂法的基础上添加松弛项,提出一种松弛高阶幂法(Relaxation Higher Order Power Method,RHOPM),提高了原有幂法的计算效率。本文主要针对由高阶马尔科夫链产生的极限概率分布问题,结合动量梯度法,提出一种新的带动量项的松弛算法(简称HOPM-NAG),并对所提算法进行收敛性分析。
1 预备知识
一个由nm个实数组成的m阶n维实张量,
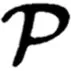
其中[n]={1,2,…,n},R为实数集,如果pi1i2…im≥0,则称为非负张量。当m=2时,上述张量就退化为矩阵。
任意一个n维列向量x∈Rn,张量-向量积定义如下:
(xm-1)i
对于任意2个n维向量x,y∈Rn,
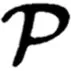

1.1 一阶马尔科夫链
马尔科夫链是一组具有马尔科夫性质的离散随机变量的集合,若集合中某一个时刻的状态只依赖于它前一个时刻的状态,则称其为一阶马尔科夫链[9]。给定一个随机过程{Xt,t=0,1,2,…}其取值属于一个代表系统状态的有限集{1,2,…,n}=〈n〉。
定义1假设有一个和时间不相关的固定概率pi,j,使得:
Prob(Xt+1=i|Xt=j,Xt-1=it-1,…,X0=i0)=Prob(Xt+1=i|Xt=j)=pi,j
其中i,j,i0,i1,…,it-1∈〈n〉。这时,称{Xt}为马尔科夫链过程。
pi,j表示从当前状态j转移到状态i的概率,有:

一阶马尔科夫链在对未来状态预测时,只用到了前一个时刻的信息,忽略了其他时刻的信息,进而影响了预测的准确性。因此,文献[4]提出一种可以充分利用历史信息的高阶马尔科夫链模型。
1.2 高阶马尔科夫链
定义2假设存在一个与时间无关的固定概率pi1,i2,…,im,
0≤pi1,i2,…,im=Prob(Xt+1=i1|Xt=i2,…,Xt-m+2=im)≤1
(1)

文献[7]将高阶马尔科夫链的极限概率分布问题转化为张量-向量积形式:
x=
(2)

初始化:给定转移概率张量,最大执行步数kmax,初始向量x0,满足x01=1,容忍误差ε。 (1)令k=1; (2) xk=xm-1k-1; (3)令δ=xk-xk-11,如果δ≤ε,算法停止,输出xk;否则,令k=k+1,返回步骤2。
文献[8]在高阶幂法的基础上增加了松弛项,提出松弛高阶幂法,主要步骤如下。

初始化:给定转移概率张量,最大执行步数kmax,初始向量x0,满足x01=1,松弛参数β,容忍误差ε。 (1)令k=1; (2) yk=xm-1k-1,^xk=βyk+(1-β)xk-1,xk=proj(^xk); (3)令δ=xk-xk-11,如果δ≤ε,算法停止,输出xk;否则,令k=k+1,返回步骤2。
2 带动量项的松弛算法及收敛性分析
高阶马尔科夫链的极限概率分布问题在一定程度上可以转化为一个优化问题:

(3)
一定程度上f(x)的梯度可以表述为:f(x)=x-xm-1,针对优化问题(3)的梯度下降法具有如下迭代格式:
xk=xk-1-αf(xk-1)=xk-1-α(xk-1-
(4)
当α=1时,求解优化问题(3)的梯度法即为高阶幂法。
动量梯度法[10]是在原始梯度下降法中加入“动量项”,可以充分利用历史梯度信息来加快梯度法的效率。针对矩阵情形,Xu等[11]提出一种带动量项的加速幂法。
Nesterov动量加速法[12]是深度学习和人工智能中常用的加速一阶算法,其迭代格式为:
Kim等[13]在Nesterov动量梯度法的基础上增加了一个松弛项γ(yk+1-xk)。受文献[11-13]的启发,本文提出一种带NAG型动量项的松弛高阶幂法HOPM-NAG。

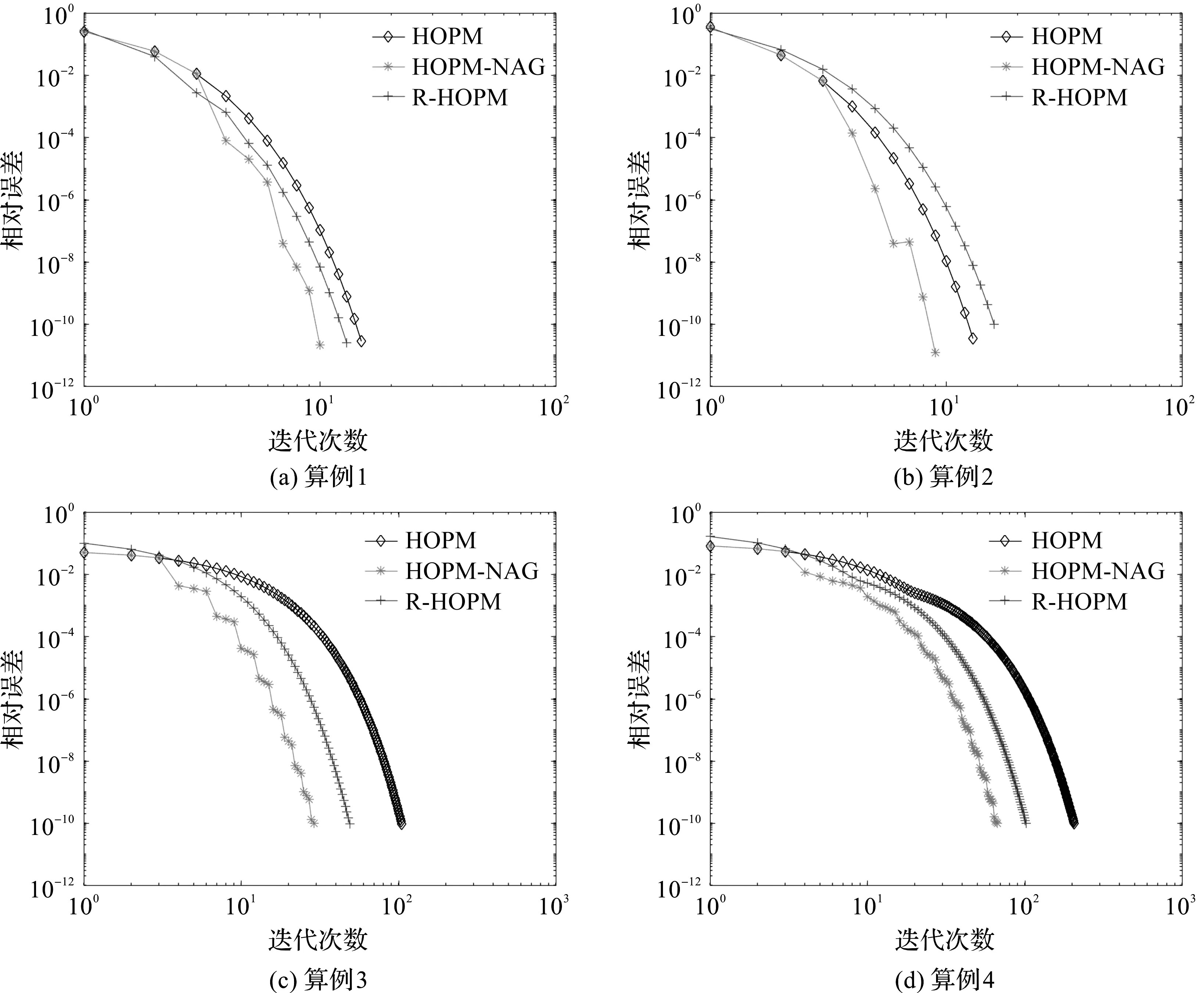
初始化:给定转移概率张量,最大执行步数kmax,动量参数β,γ,初始向量x0,y0=x0满足x01=1,容忍误差ε。令k=1,当k 在HOPM-NAG算法中,步骤1是式(4)中当α=1时的梯度下降法。步骤2中,β(yk-yk-1)称为动量项,γ(yk+1-xk)称为松弛项。 文献[7-8]给出了如下结果。 引理1[7]如果是m阶n维的非负张量,存在非零非负向量满足张量方程(2),当是不可约张量,向量是正的,如果张量方程(2)将有唯一解,δm定义如下: 其中,S⊂〈n〉,S′是S在〈n〉中的补集。 引理2[8]如果是m阶n维的非负张量,x,y∈Rn,是n维随机向量,则有: 其中ηm=(1-δm)(m-1),显然0≤ηm<1。 基于以上引理,给出HOPM-NAG算法的收敛性分析。 定理1如果是m阶n维的非负张量且记是张量方程(2)的解,当时,由HOPM-NAG算法产生的迭代序列{xk}收敛到并且满足: 当mod(k,3)≠0时,HOPM-NAG算法执行高阶幂法迭代步,产生的迭代序列{xk}满足: (5) 当mod(k,3)=0时,通过HOPM-NAG算法得到: (6) 式中,β>0,γ>0,将yk=和代入式(6)得: γ (7) 由引理2得: (8) 将式(8)带入式(7)得: 通过引理3,有: (9) 当0<κm<1时,由式(5),式(9)可以进一步证明,对∀k≥1有: 实验在Windows 10操作系统下的MATLAB R2016b中完成,硬件配置为Intel(R)Xeon(R)W-2145CPU@3.70GHz。 使用文献[7]给出的4个经典算例进行数值实验。4个算例为:(1)DNA序列{A/G,C,T};(2)DNA序列{A,C/T,G};(3)物理学家职业流动数据;(4)风力数据。 表1 不同算法在算例中的参数 从算法的迭代步数、运行时间及相对残差3个方面进行比较分析,实验结果如表2所示。 表2 不同算法求解算例的结果 从表2可以看出,对于同一个概率转移张量,与HOPM算法和R-HOPM算法相比,本文提出的HOPM-NAG算法的运行时间明显减少。 在容忍误差相同的情况下,分别采用HOPM算法、R-HOPM算法和HOPM-NAG算法进行求解,不同算法的迭代步数与相对误差的关系如图1所示。 图1 不同算法的相对残差与迭代步数的关系 从图1可以看出,同一个算例中,在容忍误差相同的情况下,HOPM-NAG算法求解极限概率分布所用的迭代步数比其他2种算法更少,说明HOPM-NAG算法的收敛速度最快,算法效果最优。 本文提出一种带NAG型动量项的松弛高阶幂法,采用周期间隔的动量外推,通过选取合适的参数来求解极限概率分布问题。与高阶幂法、松弛高阶幂法相比,本文所提算法的运行时间更短,迭代步数更少,显示了一定的优越性。但是,本文算法没有给出动量参数和松弛参数的选取规则,后续将针对这个问题展开进一步研究。





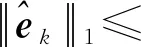
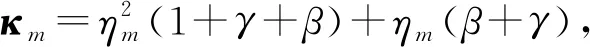

3 数值实验



4 结束语

