针对多重故障多智能体系统的容错控制方法
刘梦舒,柯彦冰,王爱民,刘智浩,李建宁
(1.杭州电子科技大学圣光机联合学院,浙江 杭州 310018;2.杭州电子科技大学自动化学院,浙江 杭州 310018)
0 引 言
早在20世纪70年代,人们就开始对多智能体系统领域进行探索。多智能体系统应用广泛,研究方向多样,如一致性问题、分布式控制问题等。文献[1]对动态智能体网络系统的稳定性进行判断,提出一种使系统能够保持一致性的方法。文献[2]针对一种具有任意邻接权值的时变时滞二阶多智能体系统,采用李雅普诺夫等方法,实现了领导智能体和跟随智能体的一致性。同时,马尔科夫跳变系统与多智能体系统相结合也是一个研究热点。文献[3]提出一种基于H∞性能指标进行故障检测与隔离的方法,在马尔科夫跳变系统框架下,研究多智能体系统网络的故障检测与隔离问题。在系统发生故障时,容错控制可以保持系统的稳定运行。文献[4-9]对执行器故障的控制问题展开研究,文献[4]研究具有执行器故障的马尔科夫非线性系统的自适应滑模控制问题,文献[5]研究乘性故障发生时的非线性多智能体系统的分布式事件触发控制策略,文献[7]针对执行器故障和绝对未知的非线性干扰同时发生时的马尔科夫跳变系统,设计了一种异步自适应容错控制器,对故障的值和扰动的边界进行估计,使得系统具有更强的鲁棒性。文献[10]对具有执行器偏移故障的多智能体系统进行故障估计,并设计了相应的容错控制器。本文针对未知执行器偏移故障以及执行器部分失效故障同时发生时的随机多智能体系统展开研究,设计了一种混合无源/H∞故障观测器,并根据估计得到的故障信息,设计了一种满足混合无源/H∞性能指标的容错控制器,实现了多智能体系统的容错一致性。
1 预备知识
定义[11]建立如下系统模型:
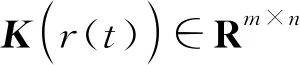
则称以上系统具有混合无源/H∞性能指标γ,α∈[0,1]为H∞性能和随机无源性能之间的权重参数。
2 问题分析及模型建立
第a个马尔科夫跳变多智能体系统模型的动力学方程如下:
(1)
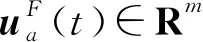
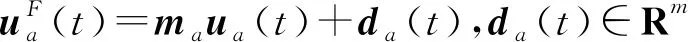
(2)
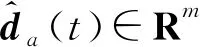
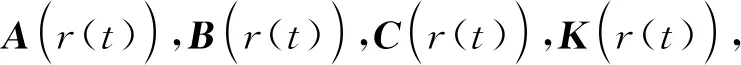
(3)
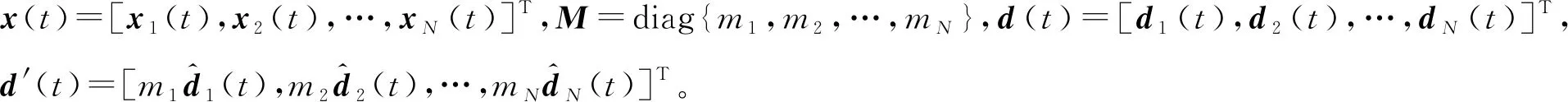
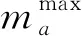
M0=diag{m01,m02,…,m0N},R=diag{r1,r2,…,rN},Q=diag{q1,q2,…,qN},|Q|=diag{|q1|,|q2|,…,|qN|}。
3 多重故障下的混合无源/H∞故障估计器
(4)
假设d(t)可导,令Fp=d(r-p)(t),p=1,2,…,r。式(4)相对应的増广系统为:
(5)
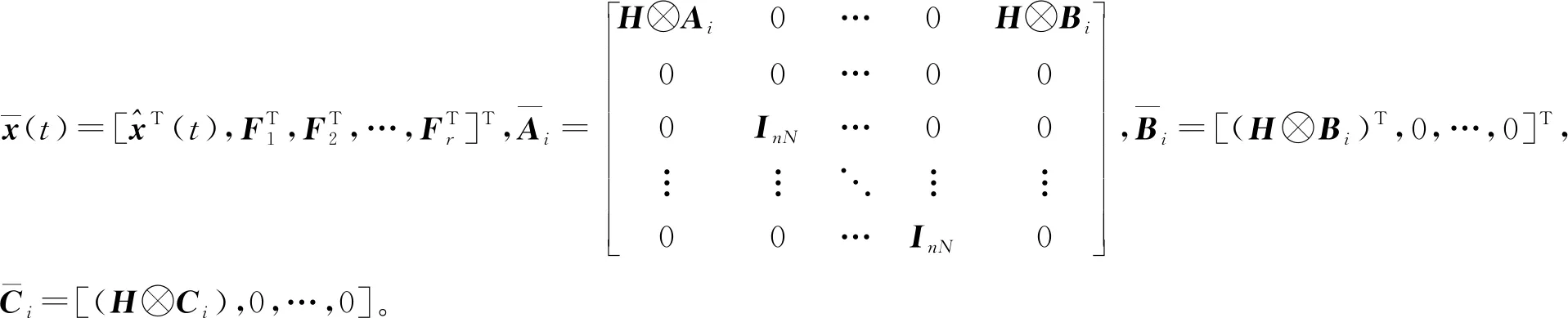
为了进一步估计未知的执行器偏移故障,设计如下故障估计器:
(6)
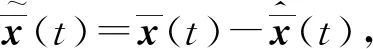
根据式(5)和式(6),可以得到:
(7)
针对系统(7),提出以下定理来设计混合无源/H∞故障估计器。
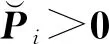
(8)
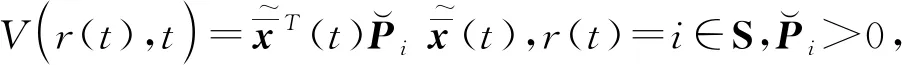

(9)

根据自由权矩阵的方法,可得:
(10)
定义
(11)
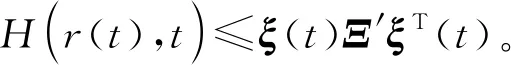
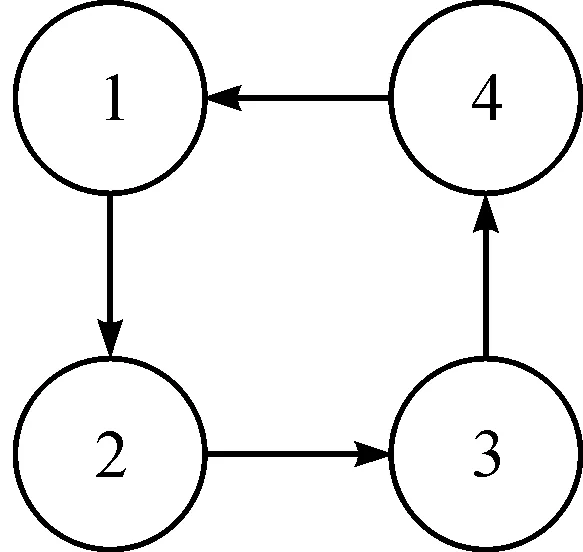
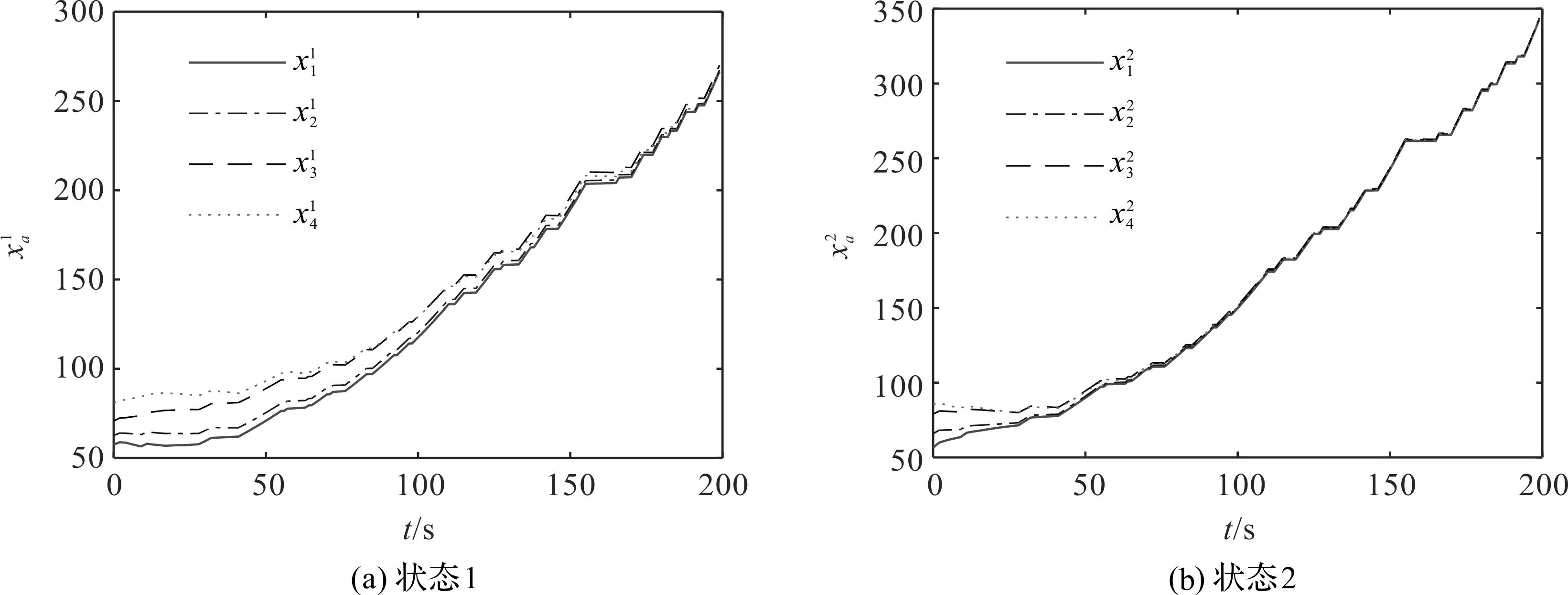
根据|Q|≤R 由于d′(t)被用于补偿d(t),控制初期不可避免地存在补偿误差,定义补偿误差为ed(t)=d(t)-d′(t),系统式(4)重新写为: (12) 针对系统(12),提出以下定理来设计混合无源/H∞容错控制器。 (13) (14) 自由权矩阵为: (15) 假设 (16) 因为|Q|≤R≤IN,根据不等式运算法则可以得到: 运用S-procedure引理[12]和Schur补引理[13]可以得到不等式(13)。证毕。 采用MATLAB R2019仿真软件模拟多智能体系统运行状态,对本文设计的故障估计器和容错控制器方法的有效性进行验证。 仿真参数设置如下: Laplacian矩阵L以及{r(t)}的跳变概率变化率矩阵Tr为: 每个智能体都有4个模态,采用的多智能体的拓扑结构如图1所示。 图1 拓扑结构 智能体每个模态的参数为: Ca1=Ca2=Ca3=Ca4=I2,δ=0.90,d(t)=sint。 每个智能体执行器部分失效故障的上下界分别为: 使用MATLAB仿真中的线性矩阵不等式来求解定理2,得到如下容错控制器增益: 图2 多智能体系统的运行轨迹 从图2可以看出,多智能体的状态1和状态2运行轨迹趋于一致,说明本文所设计的容错控制器实现了4个智能体的容错一致性。 本文针对故障多智能体系统的故障估计与容错控制器的设计展开研究。运用Lyapunov函数、自由权矩阵等方法,提出一种容错控制方案,使得故障系统4个智能体的运行轨迹趋于一致,提高了系统的稳定性能。但是,本文设计只考虑执行器偏移故障和部分失效故障同时发生的情况,下一步将针对执行器卡死故障发生的情况展开研究。4 多重故障下的混合无源/H∞容错控制器
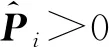
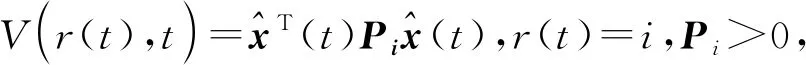


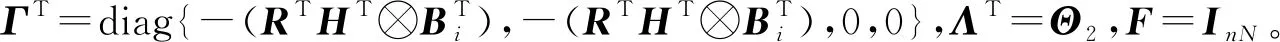
5 数值仿真与分析
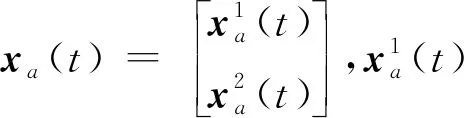
6 结束语

