视角各异皆有思 解法纷呈亦自然
——2021年全国甲卷理科第15题
栾 功
(广西南宁市第三中学 530021)
纵观历年高考,圆锥曲线的定义、标准方程、性质与平面几何的综合成了命题热点,试题贴近教材,低起点、宽入口的特点给考生提供了多角度的思考空间,思维灵活,解法多样.如果教师在教学中能充分挖掘真题的价值,对于培养学生逻辑推理能力,数学运算等能力将大有裨益.
1 试题呈现
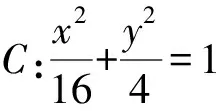
分析试题以椭圆焦点F1,F2和椭圆上关于中心对称的两点P,Q为顶点设计了四边形PF1QF2,其内涵丰富,构图灵活,有利于考生从不同角度入手求解.
2 试题解法
解法1如图1,在四边形PF1QF2中,有|PQ|=|F1F2|,且O为PQ与F1F2的中点.
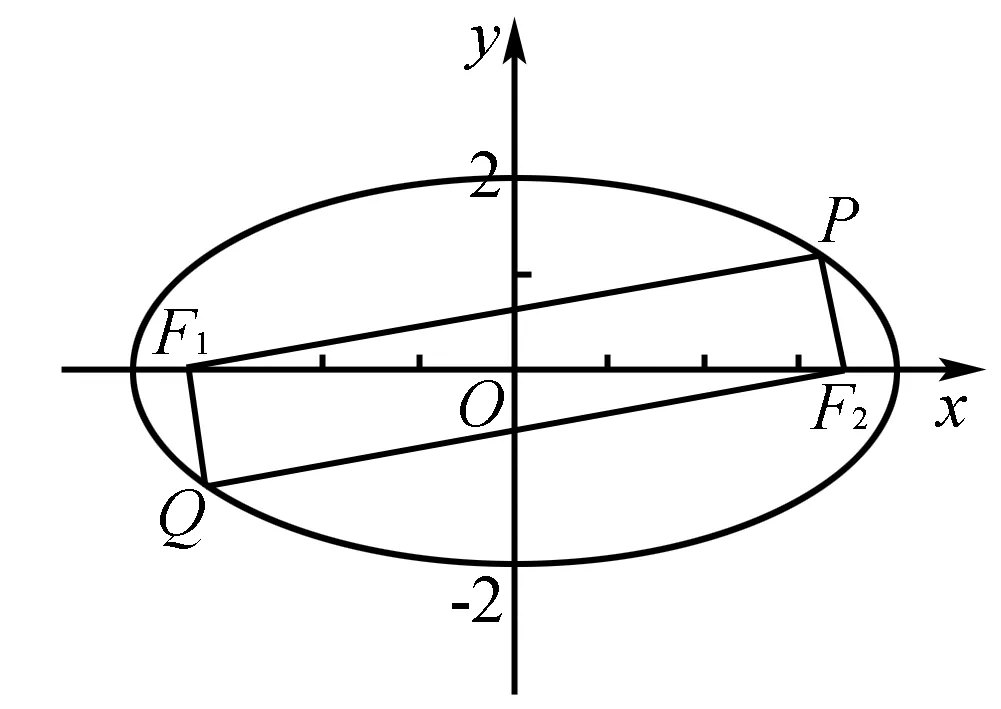
图1
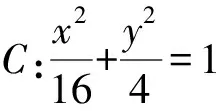
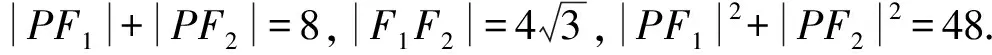
故|PF1|·|PF2|
从而SPF1QF2=|PF1|·|PF2|=8.
解法2 设P(x0,y0),由题设知
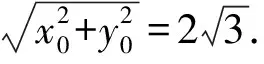
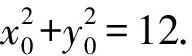
①
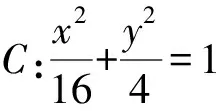
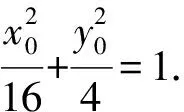
②
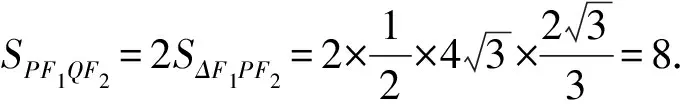
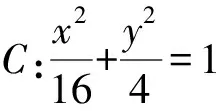

设P(4cosθ,2sinθ),则
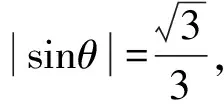
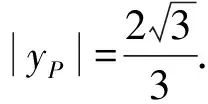
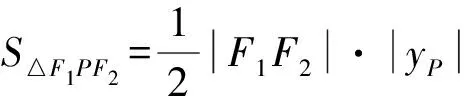
从而SPF1QF2=2S△F1PF2=8.
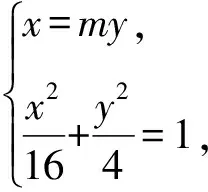
(4+m2)y2-16=0.
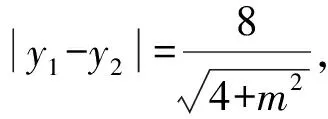
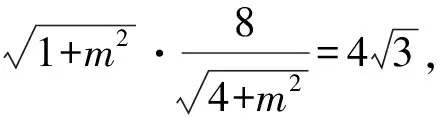
解得1+m2=9.
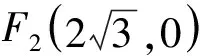
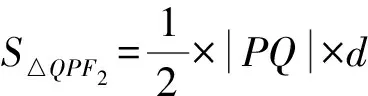
所以SPF1QF2=2S△PQF2=8.
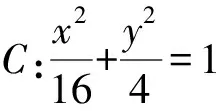
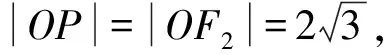
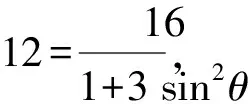
所以SPF1QF2=2S△F1PF2=4S△POF2
解法6设直线PQ的参数方程为
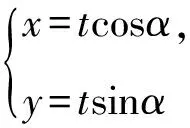
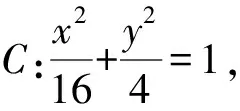
t2(cos2α+sin2α)=16.
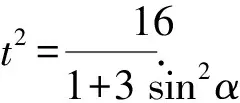
记点P,Q对应的参数分别为t1,t2,
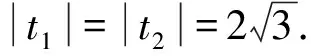
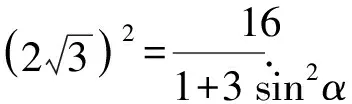
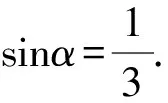
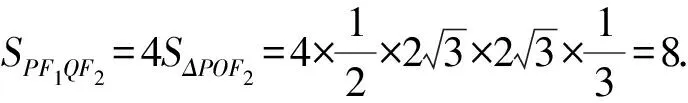
3 试题变式
通过探究我们得出了试题的六种解法,虽精彩纷呈,但仍感意犹未尽,我们尝试从不同的立场,不同的方面来观察题目,改变问题的结构形式,革新问题的曲线背景,在变式探究中进一步培养学生的逻辑推理能力、数学运算等能力.
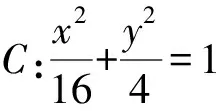
解析记四边形AOBD的面积为S,如图2,连接OD,设D(4cosθ,2sinθ),则
S=S△OAD+S△ODB
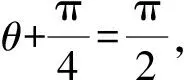
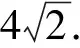

图2 图3
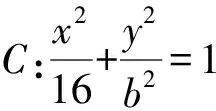
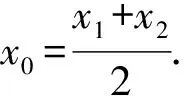
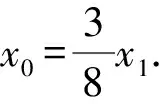
故圆D的方程为
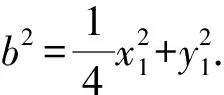
③
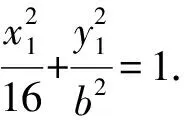
④
联立③④,得b2=4.
所以椭圆C的短轴长为4.

所以4c2=16+4a2.
所以5a2=4+a2,解得a=1.
数学家陈省身曾言:“数学是自己思考的产物,首先要能够思考起来,用自己的见解和别人的见解交换,才会有很好的效果.”数学思考是数学教学行为中最有价值的行为,在高三复习备考中,我们要充分挖掘高考真题的学习价值,引导学生对问题展开深入思考,通过一题多解、一题多变、多题一解构建知识网络,深化理性思维,感悟数学本质,提升数学素养,破除“应试教育”.

