对一道高一期末考试题的解法探究与推广
董 强
(陕西省西安市第八十五中学 710061)
基金项目:陕西省教育科学“十三五”规划2020年度课题“基于学科核心素养的高中数学单元教学设计研究”(项目编号:SGH20Y0157).
直线和圆是解析几何初步的重要研究对象,主要培养学生树立良好的“坐标法”意识,形成用代数的方法求解几何问题的基本解析思想,为后续进一步学习圆锥曲线打下坚实的基础.本文以2019年河南南阳一中高一期末考试直线和圆的综合性试题为例,通过对试题的不同解法进行探究,得到了一些有趣的结论,同时也促进学生对解析几何试题求解思路进行梳理与总结,提高学生学习数学的兴趣.
1 试题再现
题目(2019年河南南阳一中高一期末考试题)在平面直角坐标系xOy中,圆O:x2+y2=4与坐标轴分别交于点A1,A2,B1,B2.
(1)点Q是圆O上除A1,A2外的任意点(如图1),直线A1Q,A2Q与直线y+3=0分别交于不同的两点N,M,求|MN|的最小值;
(2)点P是圆O上除A1,A2,B1,B2外的任意点(如图2),直线B2P交x轴于点F,直线A1B2交A2P于点E.设直线A2P的斜率为k1,直线EF的斜率为k2,求证:2k2-k1为定值.

图1 图2
2 解法探究
2.1 第(1)问解析
解法1 符合题意的点Q应在x轴下方.
由对称性可知,点Q位于点B1时,|MN|最小.因为△A1B1A2∽△NB1M,|OB1|=2,|A1A2|=4,点B1到MN的距离等于1,所以|MN|=2,即|MN|的最小值为2.
解法2取MN的中点C,连接QC,因为∠MQN=90°,所以|MN|=2|QC|.
所以要求|MN|的最小值,即求|QC|的最小值.
由图1可知,当点Q位于点B1时,|QC|取得最小值,为|-3-(-2)|=1.
所以|MN|的最小值为2.
解法3符合题意的点Q应在x轴下方.
设Q(a,b),则-2≤b<0,易知A1(-2,0).

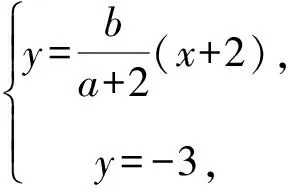


因为-2≤b<0,所以当b=-2时,|MN|的最小值为2.


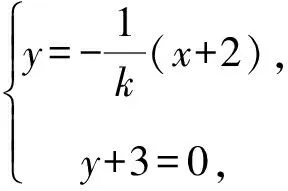

所以直线A1Q与直线y+3=0的交点为N(3k-2,-3).

当k>0时,
当且仅当k=1时等号成立;
当k<0时,
当且仅当k=-1时等号成立.
故|MN|的最小值为2.
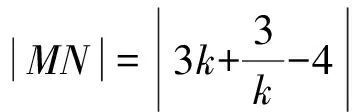
2.2 第(2)问解析
解法1由题意可知,A1(-2,0),A2(2,0),B1(0,-2),B2(0,2).
因为直线A2P的斜率为k1(k1≠0),所以直线A2P的方程为y=k1(x-2).




直线A1B2方程为x-y+2=0.

所以直线EF的斜率

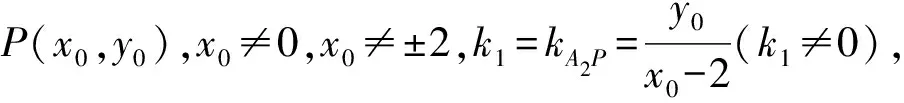
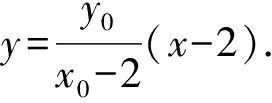
直线A1B2的方程为y=x+2.




直线EF的斜率




因为点P在圆O:x2+y2=4上,



因为点E在A2P上,所以y1=k1(x-2).

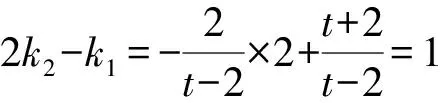
解析第(2)问中的三种证法都是通过直线方程求出交点的坐标,表示出有关直线的斜率,进而代入待求式子2k2-k1直接进行化简,有效考查了学生的运算能力,三种不同的设点方式化简时的难易程度不尽相同,解法2中最后一步要充分利用点在圆上符合圆的方程的特点有效代换,相比而言,解法3看似字母多,但实质化简简单,思路清晰.
3 结论推广
试题中的第(1)问对于任何圆而言,由对称性可知,均有点P在点B1处时到MN的距离最小,等于圆的半径.对于第(2)问而言,这个定值是1,圆的半径是2,那么这个定值是否与圆的半径有关?对于任意半径的圆,是否还有2k2-k1是一个定值?
结论1 在平面直角坐标系xOy中,圆O:x2+y2=r2与坐标轴分别交于A1,A2,B1,B2.点P是圆O上除A1,A2,B1,B2外的任意点(如图2),直线B2P交x轴于点F,直线A1B2交A2P于点E.设直线A2P的斜率为k1,直线EF的斜率为k2,则2k2-k1为定值1.



因为点P在圆O:x2+y2=r2上,



因为点E在A2P上,所以y1=k1(x-r).


评析从上述的探究证明中可以看出,即使圆的半径改变了,但依然保持2k2-k1是一个定值,是与圆的半径无关的常数1,这是圆的一种本质属性的反映,考虑到椭圆和圆具有很多相似的性质,该结论还可以在椭圆中进行进一步的推广.
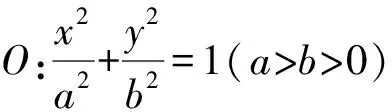

图3
证明设F(t,0),P(x0,y0),E(x1,y1),则






因为点E在A2P上,y1=k1(x-a),


解析对于结论1和结论2除了上述的证法之外,均有和原试题相似的其他证法,这里不再一一赘述.结论1可以看作是结论2的特殊情形.

