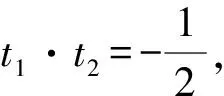一道三角函数最值问题的解法、背景及其拓展
李文东
(广东省中山市中山纪念中学 528454)
2018年全国Ⅰ卷理科数学第16题以三角函数为背景,考查三角函数求导,利用导数处理最值问题等知识,考查转化与化归思想、推理论证能力、运算求解能力、函数与方程思想,体现了数学运算、逻辑推理等核心素养,是一道难得的好题,值得我们细细研究,下面我们给出本题的几种典型的解法,然后指出其实际背景,并给出了一个简单的拓展.
1 题目呈现
题目(2018年全国Ⅰ卷16题)求函数f(x)=2sinx+sin2x的最值.
2 解法欣赏
解法1(导数法) 显然f(x)为奇函数且最小正周期为2π,故只需考虑x∈[0,π].
由于f′(x)=2cosx+2cos2x
=2(2cos2x+cosx-1)
=2(2cosx-1)(cosx+1),
令f′(x)=0,
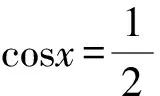

列表如下:
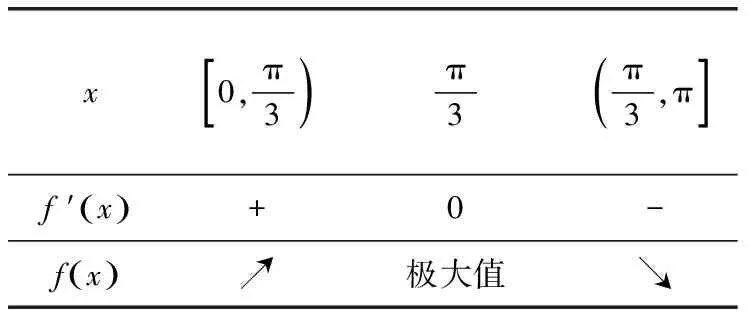
x0,π3[)π3π3,π(]f ′x()+0-fx()↗极大值↘

点评此题虽然是2018年全国高考的填空压轴题,难度并不算大,只需要按照导数求解最值的常规步骤即可,需要注意的细节是抓住f(x)为奇函数且最小正周期为2π,从而将定义域限制在x∈[0,π],这样就给单调性的讨论带来极大的方便.
解法2(非线性规划) 显然f(x)为奇函数.
故只需求出f(x)的最大值即可.
又f(x)=2sinx+sin2x=2sinx(1+cosx),
记sinx=m,cosx=n,f(x)=t,
则2m(1+n)=t

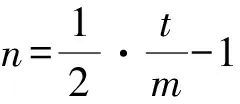

图1
设切点为(m0,n0),则有
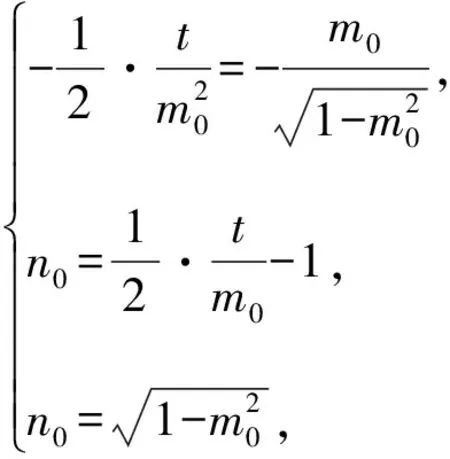
消去n0和t,得
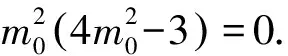
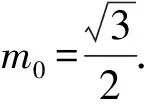


利用f(x)为奇函数知
点评令sinx=m,cosx=n,则m2+n2=1,从而将问题转化为一个条件最值问题.
解法3(待定系数法)f(x)=2sinx(1+cosx),引入参数k,根据柯西不等式和均值不等式有:
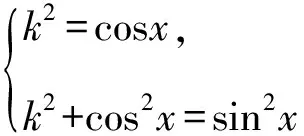
消去k2,得
cosx+cos2x=sin2x.
进一步化简,得
2cos2x+cosx-1=0.
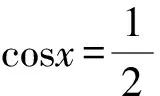
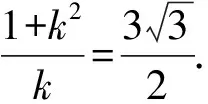

解法4(均值不等式)
因为f(x)=2sinx+sin2x
=2sinx(1+cosx),
所以[f(x)]2=4sin2x(1+cosx)2
=4(1-cosx)(1+cosx)3
当且仅当3-3cosx=1+cosx,
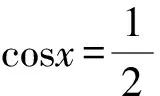
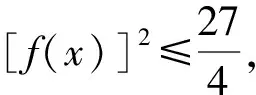


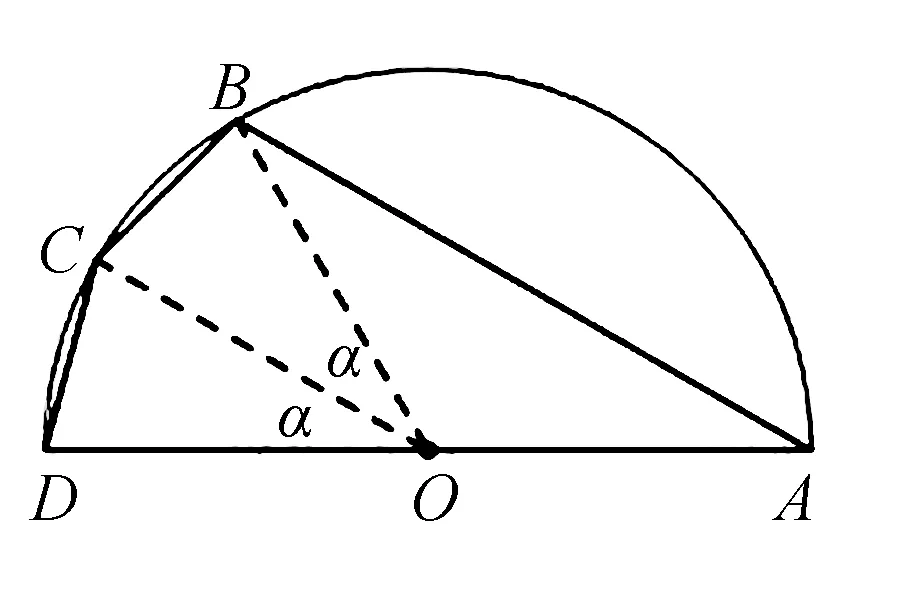
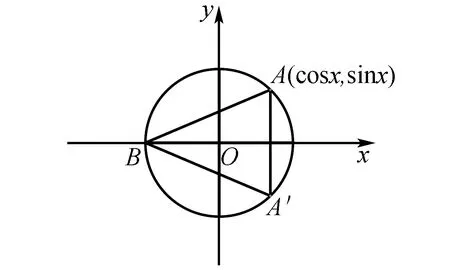
解法5(琴生不等式) 由f(x)为奇函数,我们可以限定在0 由琴生不等式,若f(x)为凸函数,则 由于y=sinx为(0,π)上的凸函数, 于是f(x)=2sinx+sin2x =sin(π-x)+sin(π-x)+sin2x 解法6(构造几何模型) 因为f(x)=2sinx+sin2x =2sinx(1+cosx), 图2 如图2,设A(cosx,sinx),点A关于x轴的对称点为A′,点B(-1,0),则 f(x)=2sinx(1+cosx)=2S△AA′B. 此题其实也有实际背景,其来源如下: 已知半圆O的直径为2,AD为直径,B,C是半圆上除直径外的两点,且BC=CD,则四边形ABCD面积的最大值为____. 图3 如图3,连接OB,OC,设∠BOC=∠DOC=α, 则SABCD=S△OBC+S△OCD+S△OAB 进一步,我们可以将此题拓展如下: 拓展求函数f(x)=sinx(a+cosx),a∈R的最大值. 解析显然f(x)的周期为2π,且有 f(2π-x)=-f(x) . 即f(x)关于点(π,0)对称. 为此我们可以限制定义域为[0,π]. f′(x)=2cos2x+acosx-1, 令cosx=t,y′=g(t)=2t2+at-1, 由于Δ=a2+8>0 g(0)=-1<0. 函数g(t)在[-1,1] 内有两个零点t1,t2, 由于y=cosx在[0,π]上单调递减, 故存在唯一的x1,x2使得 由y′=g(t)=2t2+at-1<0,解得t1 即t1 解得x1 由此可知f(x)在[0,x1]上单调递增, 在[x1,x2]上单调递减, 在[x2,π]上单调递增, 由此可知fmax(x)=max{f(x1),-f(x2)}. 代入数据计算可得: 当-1 fmax(x)=-f(x2)=-sinx2(a+cosx2) 而当0≤a<1时, fmax(x)=f(x1)=sinx1(a+cosx1) (2)当a≤-1时,函数g(t)在[-1,1] 内有一个零点t0<0. 由于y=cosx在[0,π]上单调递减, 故存在唯一的x0使得 f(x)在[0,x0]上单调递减, 在[x0,π]上单调递增, 由此可知 fmax(x)=-f(x0) (3)当a≥1时,同理可得 综上: 做百题不如钻研一题,通过对一道高考试题的多角度研究,不仅提高了我们的解题能力,而且拓展了我们的思维,使我们从题海中跳出来.

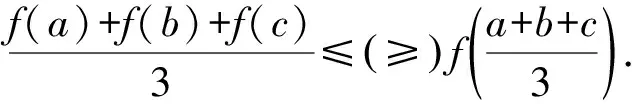

3 背景和拓展